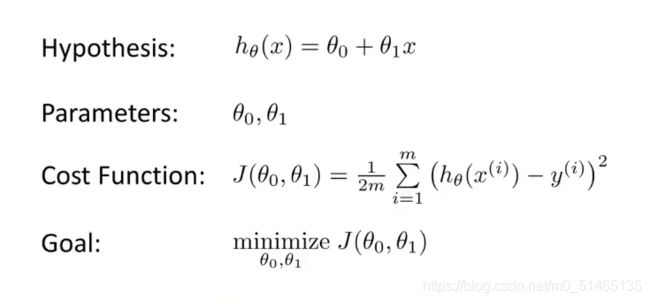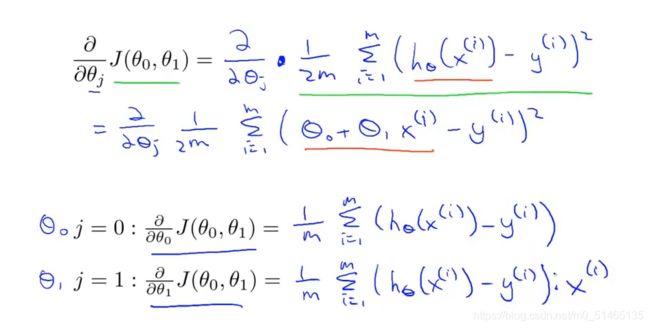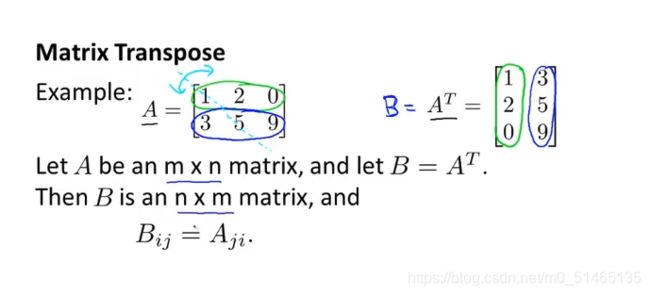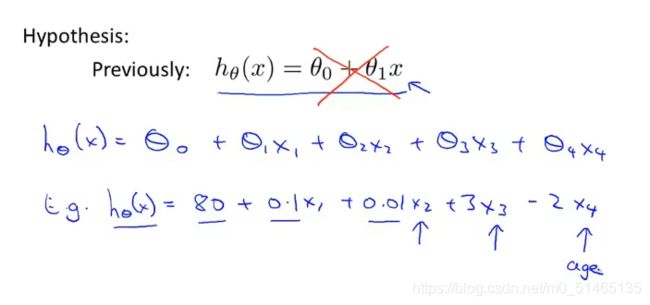吴恩达机器学习笔记

一、引言部分

1.1什么是机器学习

机器学习（Machine Learning）：1.是研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。2.一个程序被认为能从经验E中学习，解决任务 T，达到性能度量值P，当且仅当，有了经验E后，经过P评判， 程序在处理T时的性能有所提升。

1.2监督学习和无监督学习

监督学习（Supervised Learning）：对于数据集中每一个样本都有对应的标签，包括回归（regression）和分类（classification）；
无监督学习（Unsupervised Learning）：数据集中没有任何的标签，包括聚类（clustering），著名的一个例子是鸡尾酒晚会。实现公式：[W,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x’);（Octave编程语言)
有监督机器学习又被称为“有老师的学习”，所谓的老师就是标签。有监督的过程为先通过已知的训练样本（如已知输入和对应的输出）来训练，从而得到一个最优模型，再将这个模型应用在新的数据上，映射为输出结果。再经过这样的过程后，模型就有了预知能力。
而无监督机器学习被称为“没有老师的学习”，无监督相比于有监督，没有训练的过程，而是直接拿数据进行建模分析，意味着这些都是要通过机器学习自行学习探索。这听起来似乎有点不可思议，但是在我们自身认识世界的过程中也会用到无监督学习。比如我们去参观一个画展，我们对艺术一无所知，但是欣赏完多幅作品之后，我们也能把它们分成不同的派别。比如哪些更朦胧一点，哪些更写实一些。即使我们不知道什么叫做朦胧派和写实派，但是至少我们能把他们分为两个类。

二、线性模型

2.1模型描述

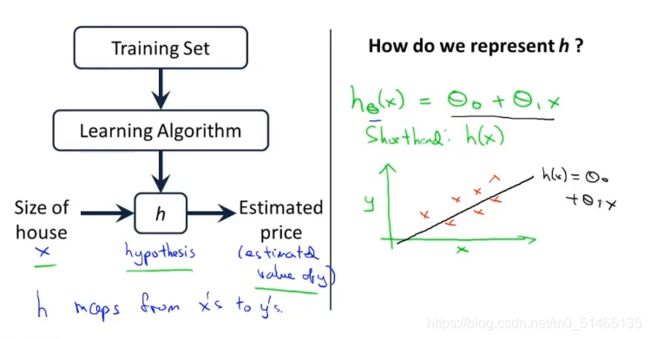
线性回归模型：hθ​(x)=θ0​+θ1​x

假设函数h(hypothesis)：是一个从输入 x 到输出 y 的映射，

2.2代价函数（用于线性回归）

数学定义：

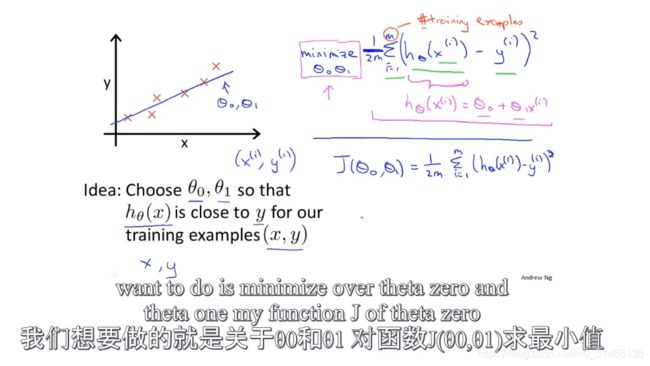θ为1时为最小化代价代价函数，此时h1(x)=x
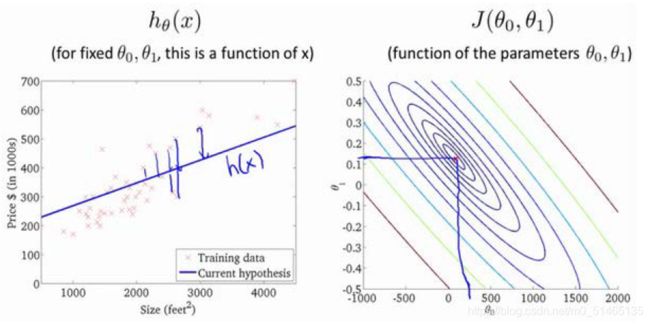
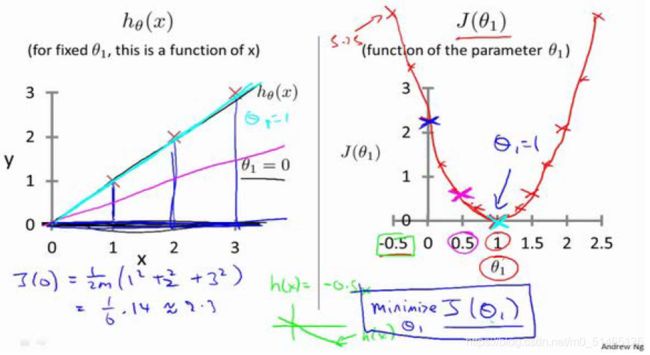代价函数的另外一个图形表示是等高图，如图所示：

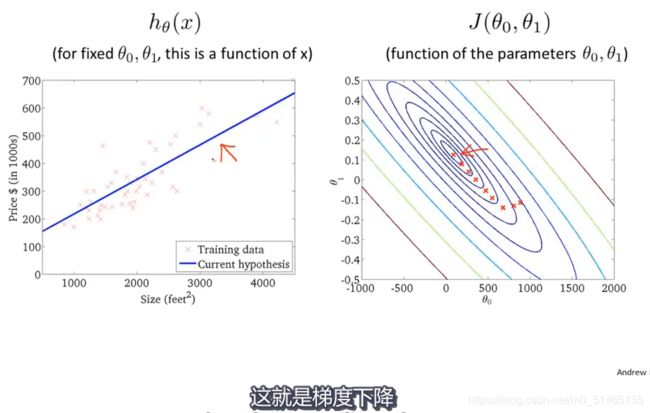
2.3梯度下降

梯度下降算法：可以将代价函数J最小化的方法

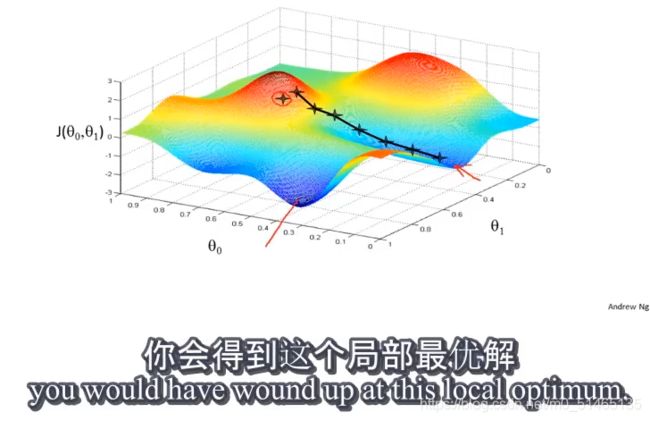
想象这张图为一座山，在梯度下降算法中 ，站在山顶旋转360度，并且问自己如果要在某个方向上走一小步，能够尽快走下山，应该向哪个方向迈步。每一个位置都有一个局部最优解，如果起始点偏移一点，你会得到一个完全不同的局部最优解。

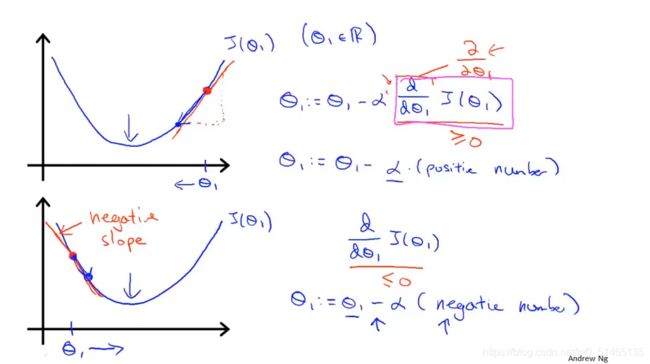
梯度下降数学原理：∂θ/j​∂​J(θ0​,θ1​)导数项的示意图
学习速率α示意图

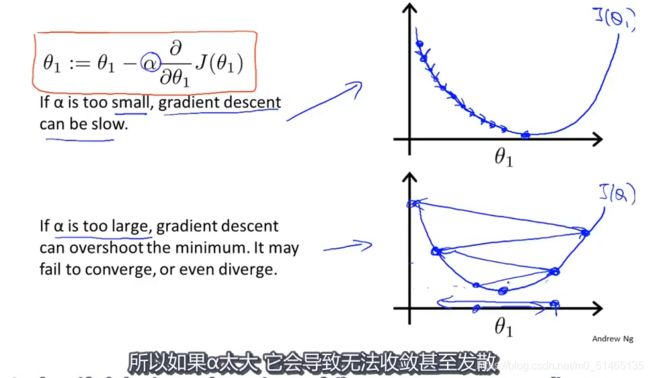
其中α为学习速率（learning rate），控制下降幅度。如果α太小，梯度下降会变得缓慢；如果α太大，梯度下降可能无法收敛甚至发散。
后面第二部分∂θ/j​∂​J(θ0​,θ1​)为导数项，当斜率≥0，θ更新后将减小，当斜率≤0，θ更新后将增加，向代价函数最小值靠拢。
越靠近局部最小值，梯度下降法会自动使得导数越来越小，即采取更小的幅度。

2.4线性回归的梯度下降（梯度下降和代价函数的结合）

目的：将梯度下降法用到最小化平方差代价函数中。

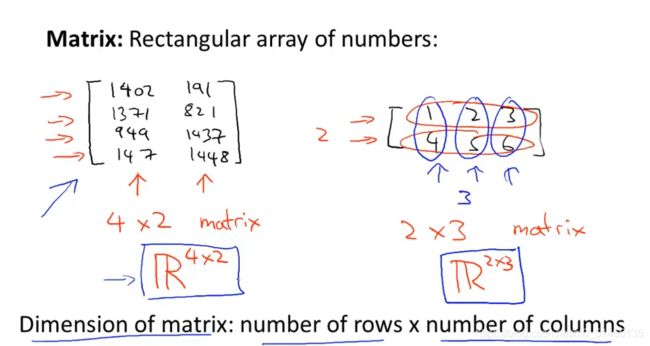
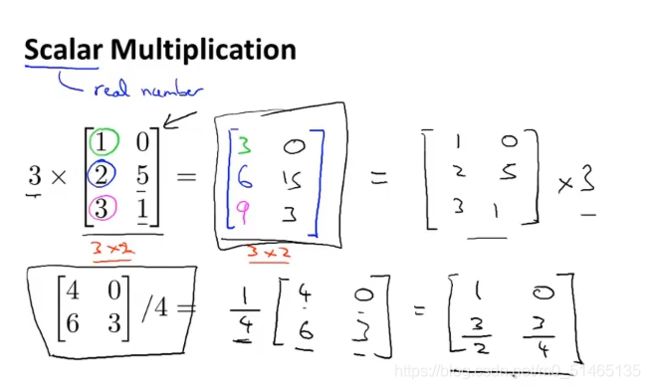
3.1矩阵与向量

复习矩阵

矩阵的加法：
矩阵的乘法：
单位矩阵：

复习向量

向量是一种特殊的矩阵，向量是只有一列的矩阵
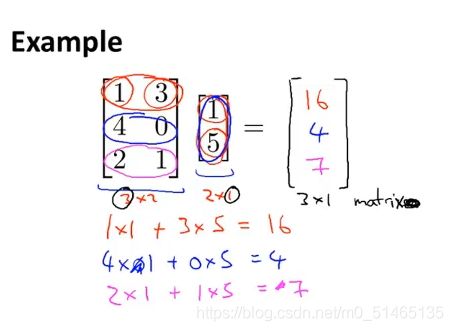
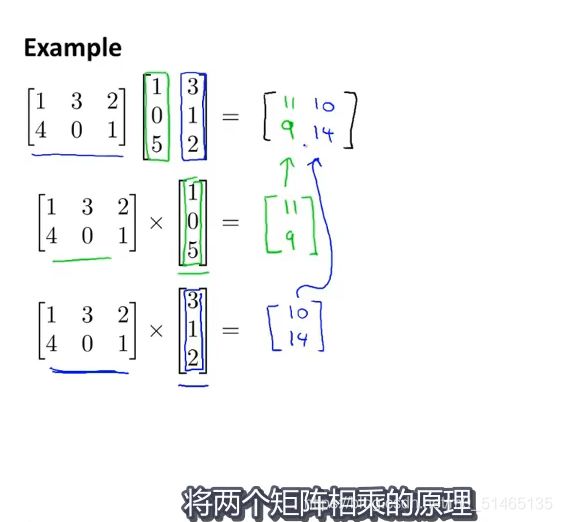
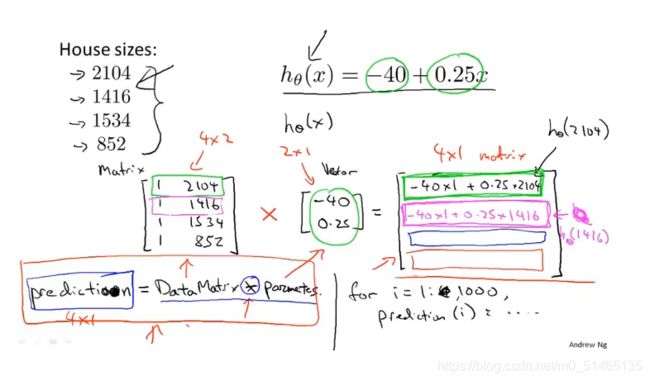
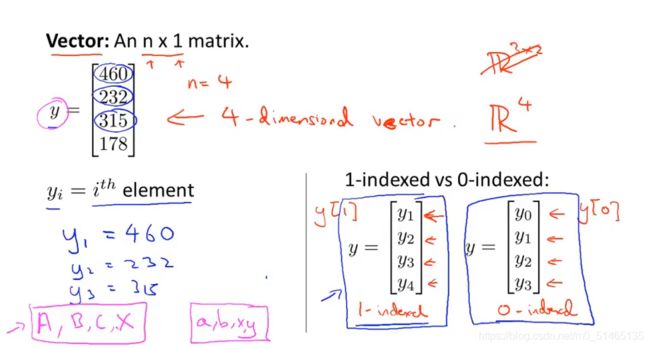用矩阵的形式计算预测值

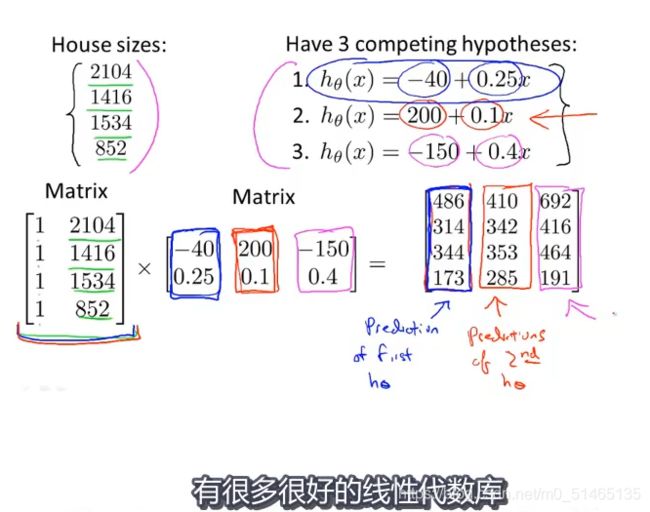
逆矩阵、转置

矩阵逆运算（逆矩阵）：
只有m×m的矩阵（方阵）才有逆矩阵，不存在逆矩阵的矩阵称为逆矩阵或者退化矩阵

矩阵的转置

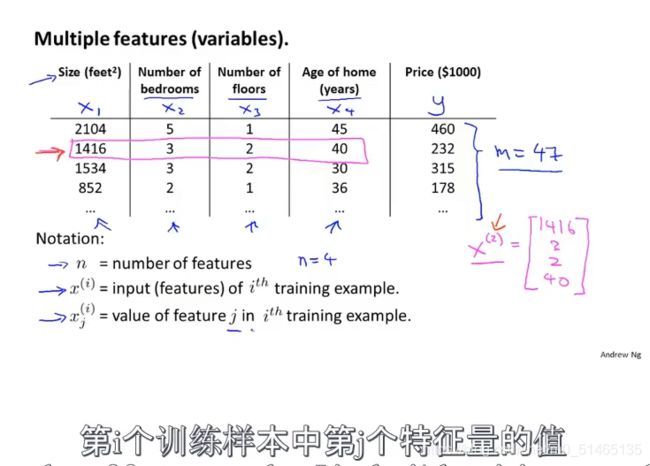
4.1多元线性方程（多特征）

多元线性回归方程
用矩阵表示线性方程

4.3多元梯度下降法

多元线性方程
一个n+1维的向量
代价函数
梯度下降
左图为单元线性回归梯度下降法，右图为多元线性回归梯度下降法，并且多元线性回归梯度下降法可推广

4.3.1多元梯度下降法之特征缩放（均值归一化）

特征缩放：确保不同特征的取值在相近的范围内，以使得梯度下降法能更快地收敛
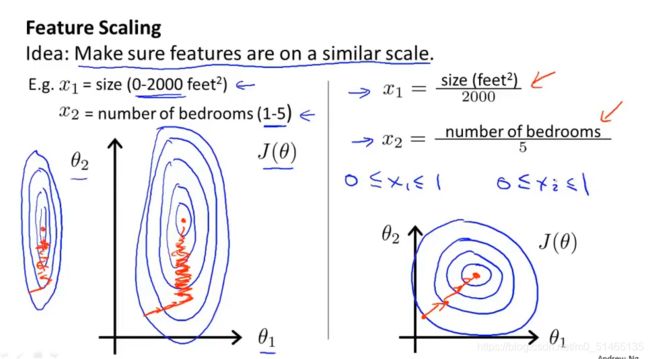特征范围的选择
均值归一化：将xi用xi-μi代替，使得特征均值为0。
Eg.例如房子的大小取值为0-2000，并且假设房子面积的平均值为1000。房子中卧室的数量取值为0-5，并且假设卧室数量的平均值为2。x1均值归一化为size-1000/2000，x2均值归一化为#bedroom-2/5
均值归一化的推广：
μ1为训练特征x1的平均值，s1为该特征值的取值范围(最大值减最小值），新的x1为平均值归一化后的特征值。

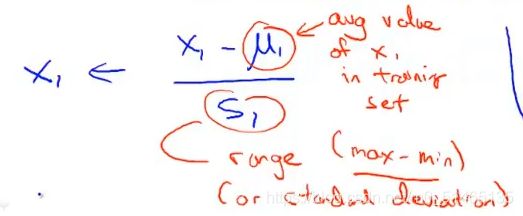
4.3.2多元梯度下降法之学习率

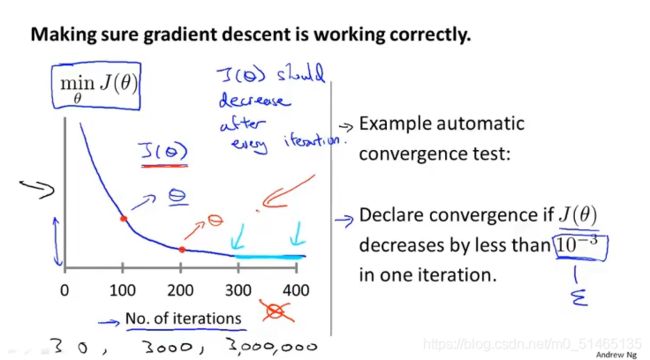
下图是梯度下降法的规则。1.在debug中确保梯度下降是正常工作的.2.如何选择学习率
1.下图为代价函数随着迭代步数的增加而变化的曲线，横轴为梯度下降的迭代次数，纵轴为代价函数值。自动收敛测试：判断梯度下降方法是否收敛，如果代价函数下一步迭代后的下降小于一个很小的值ε，这个测试就判断函数已收敛，但实际中ε值很难找出，我们更倾向于看左图。
2.如果随着迭代次数的增加代价函数反而上升了，此时应选择较小的学习率α，但也不能选择过小的α，那么梯度下降算法可能收敛得很慢
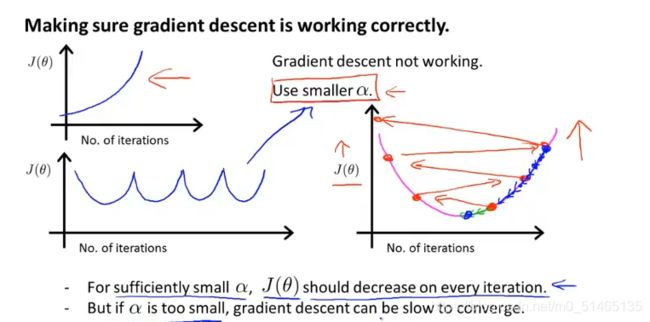总结：

4.4特征和多项式回归

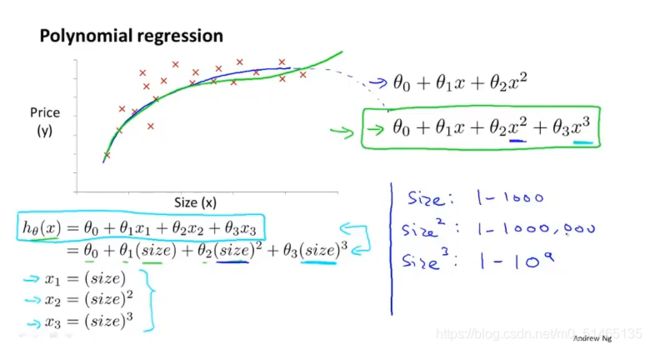
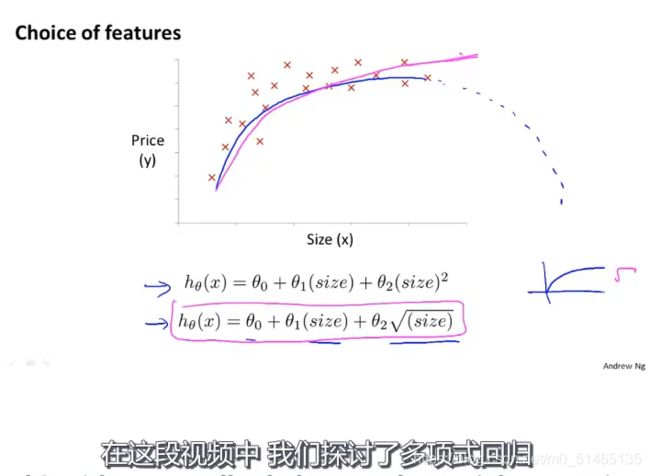
学习目标：一些可供选择的特征、如何得到不同的学习算法、多项式回归（线性回归的方法来拟合非常复杂的函数，甚至是非线性函数）

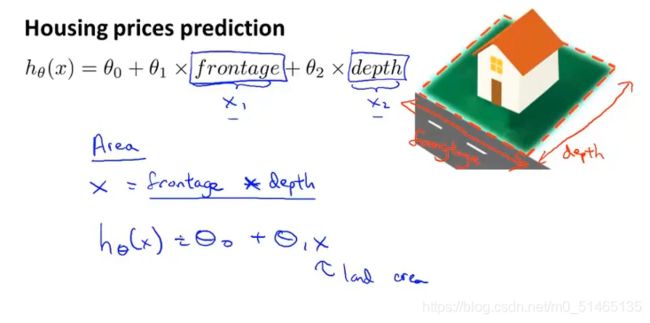
如何将模型与数据进行拟合？使用多元线性回归的方法，使用该方法特征缩放尤为重要

4.5正规方程（用于线性回归问题）

正规方程：提供了一种求θ的解析方法，可以一次性得出参数θ的最优值，使得代价函数最小。
其中m为特征维数，n为特征数

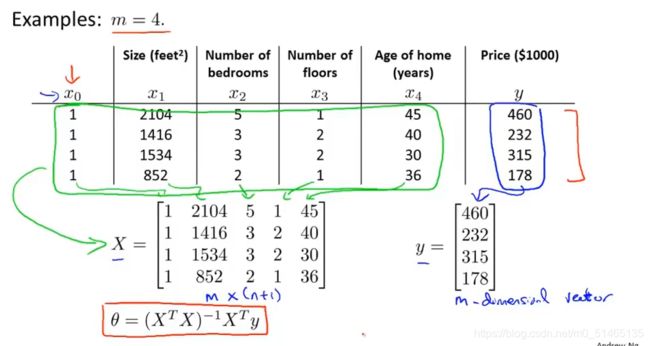
如何使用正规方程来求最优化θ：
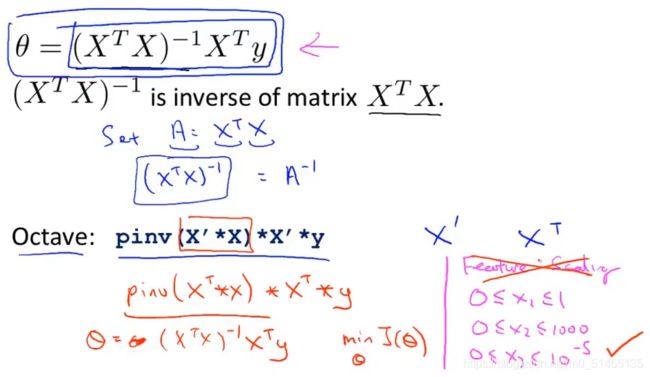梯度下降法与正规方程法的优缺点;
可能会遇到XTX矩阵不可逆的两种情况及解决方法：1.特征冗余2.特征数大于样本数（样本数少）

三、非线性模型

5.1分类（逻辑回归）

预测变量y是一个离散值情况下的分类问题

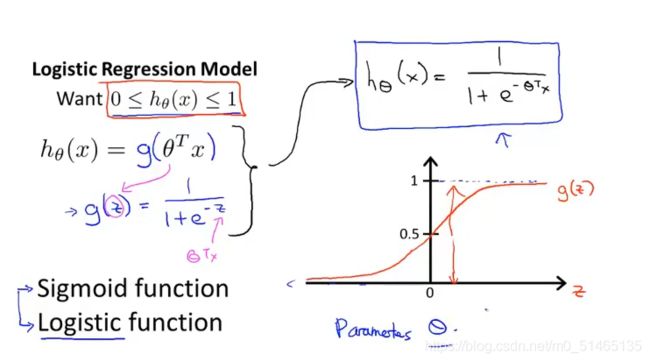
逻辑回归算法（一种分类算法），其特点在于算法的输出或者预测值一直介于0和1之间
逻辑回归函数g(z）

hθx是对于输入特征为x时y=1的概率估计

5.2决策边界

只要假设函数hθx输出y=1的概率大于等于0.5，则预测y=1为正类，另一种情况，当输出y=0的概率小于0.5，则预测y=0为反类。由于逻辑回归的假设函数hθx=g(θ^Tx),因此只要θTx大于等于0，h(x)就大于等于0.5 ，所以假设函数就会预测y=1。

简而言之，预测y=1,只需要θ^Tx大于或等于0。反之预测y=0，只需要θTx小于0

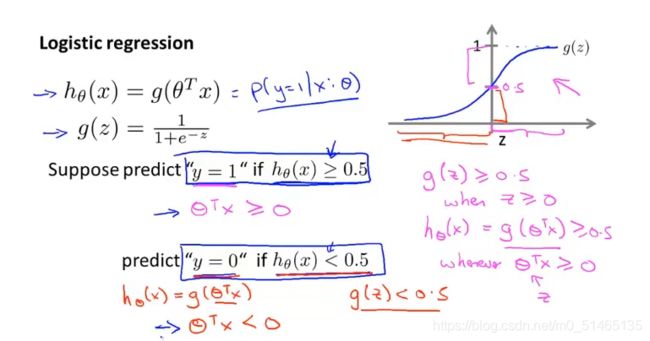
决策边界是h(x）正好等于0.5的区域
假设已经拟合好了参数θ1，θ2，θ3，决策边界上半部分预测值为1，与此相对，决策边界下半部分预测值为0
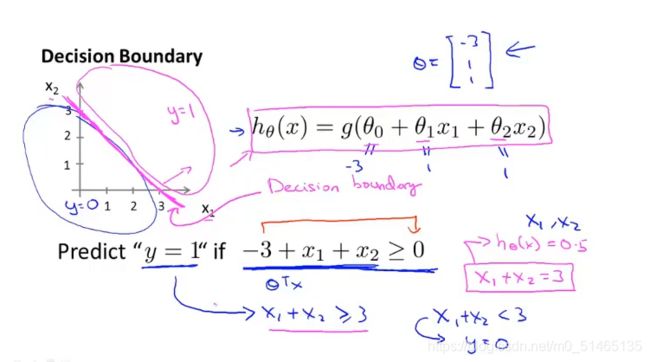非线性的决策边界

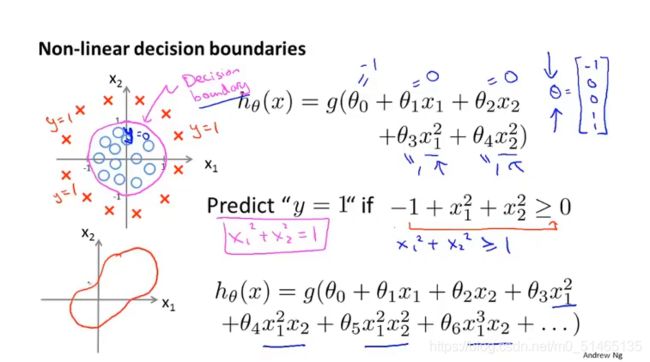
5.3代价函数（用于逻辑回归）

如何自动的拟合逻辑回归函数模型的参数θ？
若使用线性代价函数用于逻辑回归方程，会得到一个非凸函数，这样不能使用梯度下降法来找到最小代价函数
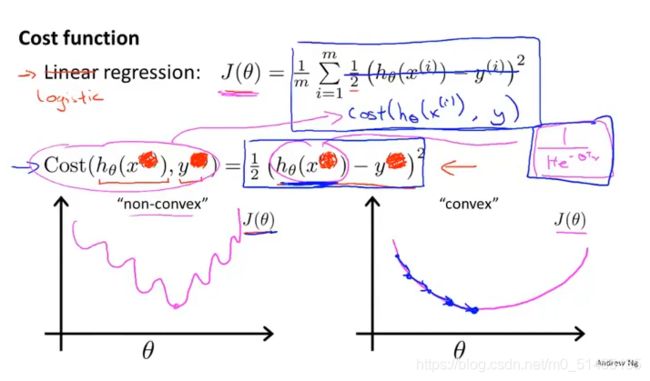用于逻辑回归的代价函数：
当预测值y=1时
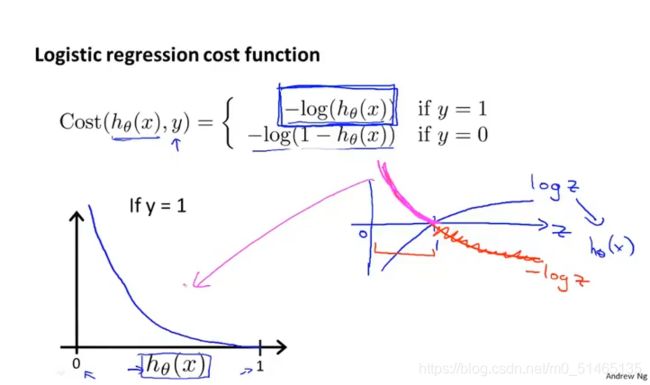
当预测值y=0时

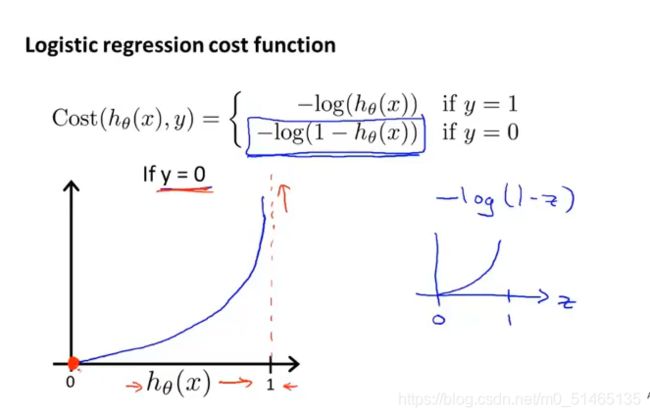
5.4简化代价函数与梯度下降

用一种方法把y=1和y=0合并成一个等式
得到简化后的逻辑回归代价函数
梯度下降法求最小代价函数：

5.5高级优化算法

5.6多元分类

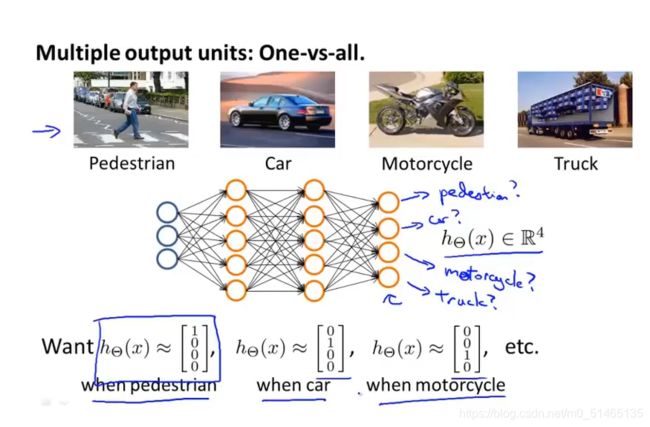
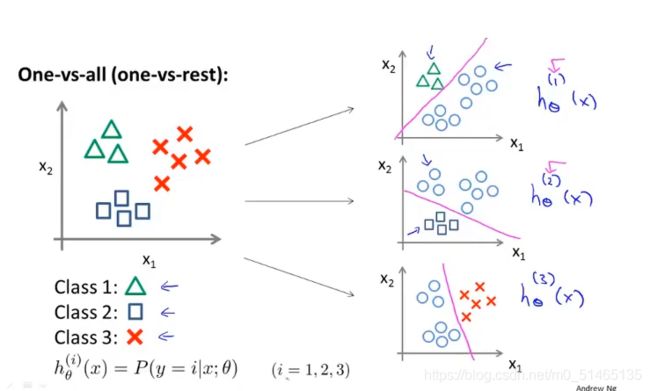
训练一个多元分类器hθix预测i类别y=i的概率，hθ1x在给定x和θ时，y的值为1的概率，，同样，hθ2x在给定x和θ时，y的值为2的概率。

6.1过拟合问题

有过多的特征，在训练集中适合，但不能很好地预测新样本

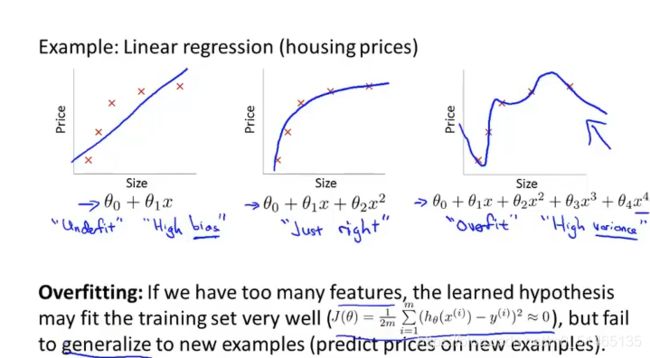
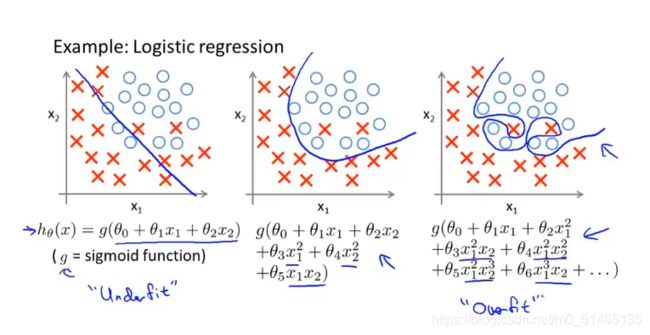过拟合的解决方法：1.选择合适的特征数量2.正则化

在函数中加入惩罚项使得θ3和θ4非常小，要最小化其均方误差代价函数，对函数进行修改，让θ3和θ4≈0

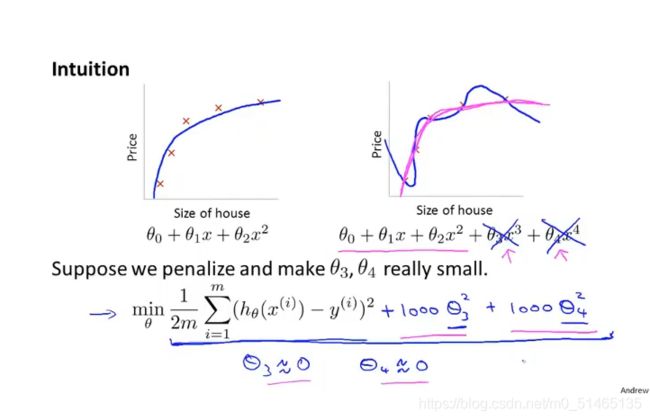
6.1.1正则化

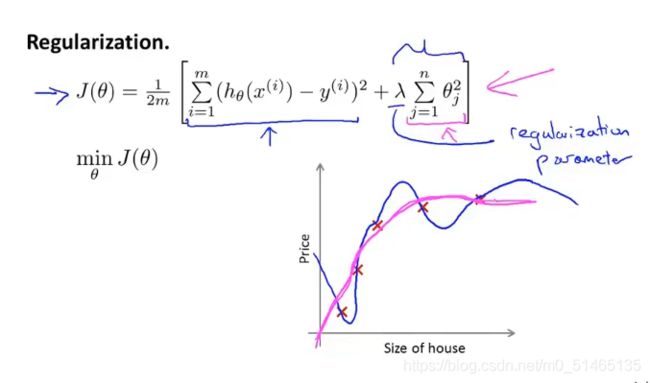
正则化的目的是使参数θ尽可能小，使假设模型变得更简单，从而解决过拟合问题。而一般情况下我们不知道该选出哪些参数，来缩小它们的值。因此在正则化中，就是修改这个代价函数，在后面添加一个额外的正则化项，来缩小每个参数的值，一般只对θ1到θn进行正则化。
λ称为正则化参数，λ的作用控制两个不同目标之间（第一项与正则项）的平衡关系。
如果正则化参数λ的值设的过大，其结果是对于第一项θ参数惩罚程度太大，那么这些参数都将接近于0，就相当于把假设函数的全部项都忽略掉了，相当于用一条直线去拟合，就意味着假设函数欠拟合。

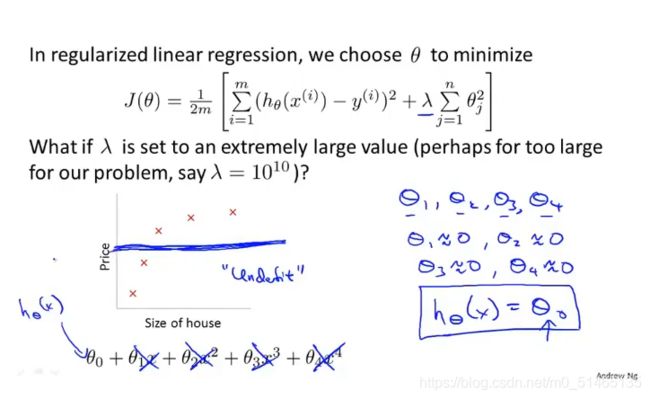
6.1.2线性回归的正则化

正则化线性回归：
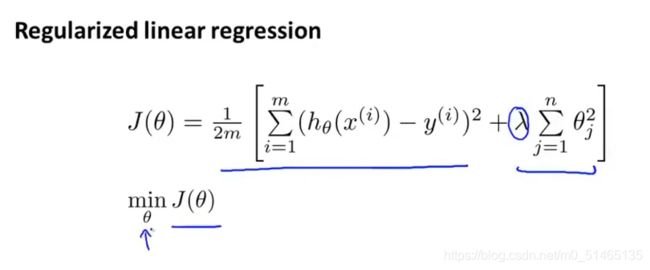在没有正则化情况下的梯度下降，来最小化代价函数（常规线性回归）
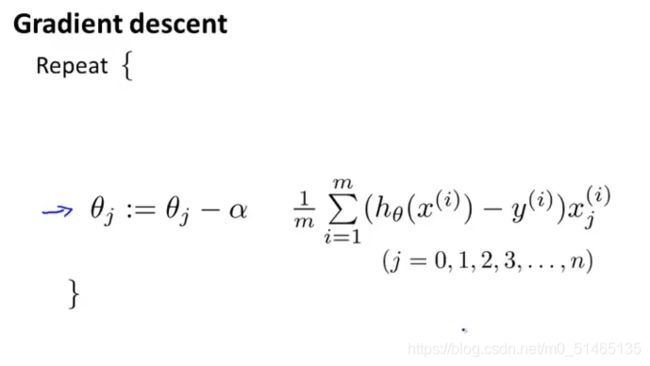在有正则化情况下的梯度下降：将θ0分离出来，因为在正则化中线性回归中惩罚的对象参数是θ1、θ2…θn
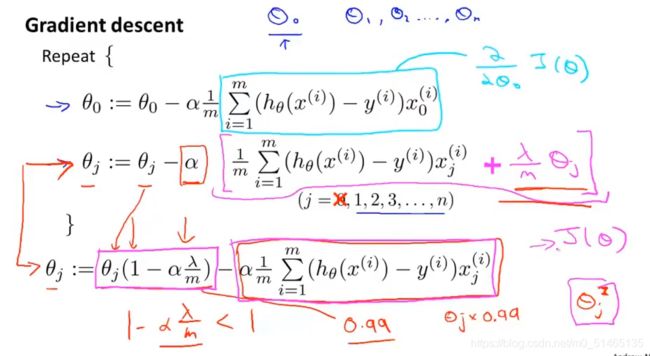正规方程：提供了一种求θ的解析方法，可以一次性得出参数θ的最优值，使得代价函数最小

没有正则化项的正规方程：

有正则化项的正规方程：

6.1.3逻辑回归的正则化

逻辑回归也会出现过拟合的情况
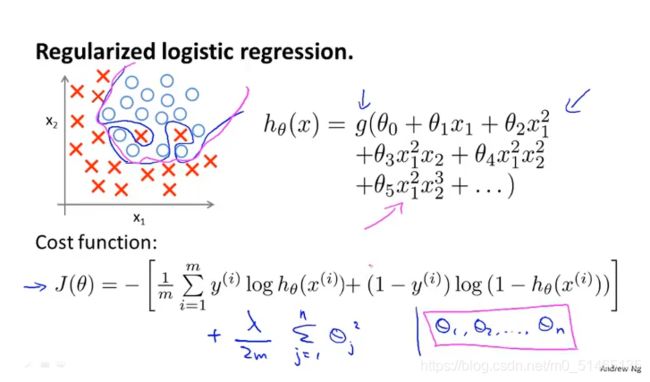没有正则项的逻辑回归梯度下降算法
有正则化项的逻辑回归梯度下降正则化梯度下降的优化算法：

四、多特征的非线性问题

7.1非线性假设（神经网络）

为什么要研究神经网络？

1.机器学习的特征个数往往很大
很多机器学习问题不止两个特征，对于这类问题，如果分析包含所有的二次项，那么在原始特征n=100的情况下，最终会有（n的二次方/2）5000个特征，而且二次项的个数大约以n^2增长；而三次项的个数是n的三次方的量级，因此当初始特征个数n很大时候，将这些高阶多项式项数，包括到特征里会使得特征空间急剧膨胀，不是个好方法，处理特征过多，运算量过大。
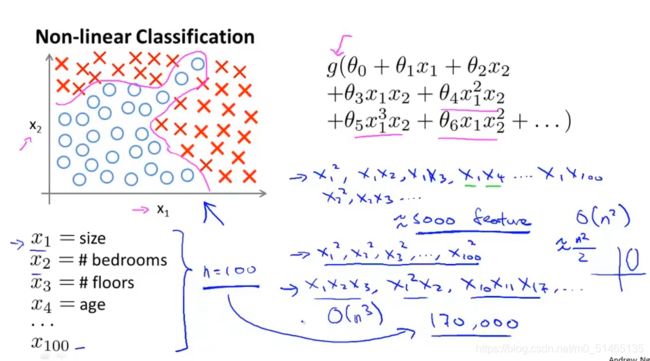2.一个计算机视觉中的例子
假设你想要使用机器学习来训练一个分类器来检测图像，来判断图像是否为一辆汽车，取出图中的一小部分，计算机看到的是一个数据矩阵，告诉我们每个像素的亮度值， 计算机根据这个像素点矩阵，这些数值代表一个汽车的门把手。
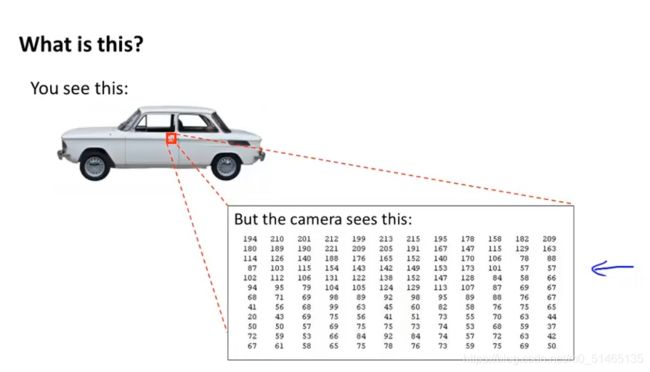
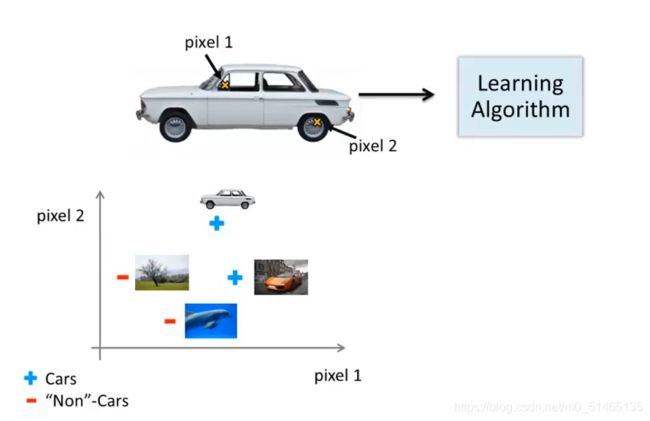
机器学习识别汽车：
首先在图片中选择两组像素点位pixel1,pixel2,在坐标中标出这幅汽车的位置，位置取决于像素点1和像素点2的强度值，再以同样的方法在坐标系中画上更多的新样本，用+表示汽车图片-表示非汽车图片，将发现汽车与非汽车分布在坐标系的不同区域，因此需要一个非线性假设来分开这两类样本。
假设空间维数50*50像素的图片，共2500个像素点，因此特征向量的元素数量为2500，如果包含所有的二次项特征来学习得到非线性假设，那么总共就有约300万个特征
因此简单的逻辑回归算法在特征n很大的时候不是一个好方法。

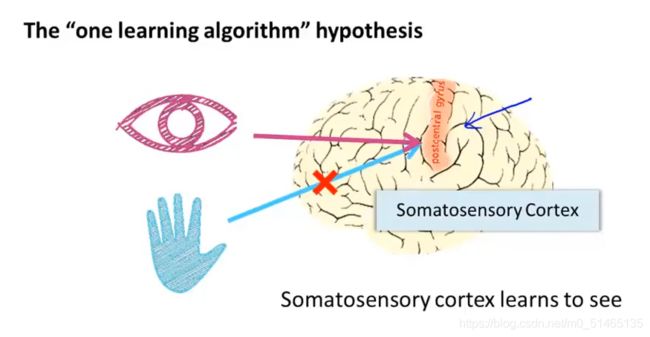
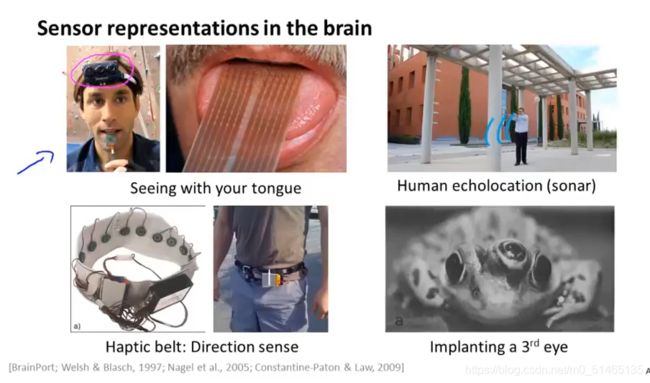
7.2神经元与大脑

神经网络的历史背景：

7.3神经网络模型展示Ⅰ

神经网络模仿了大脑中的神经源或者神经网络：神经元有细胞体(Nucleus)，神经元有很多输入通道叫做树突（Dendrite)，可以想象成输入,轴突（Axon)可以想象成输出，给其他神经元传递信号。
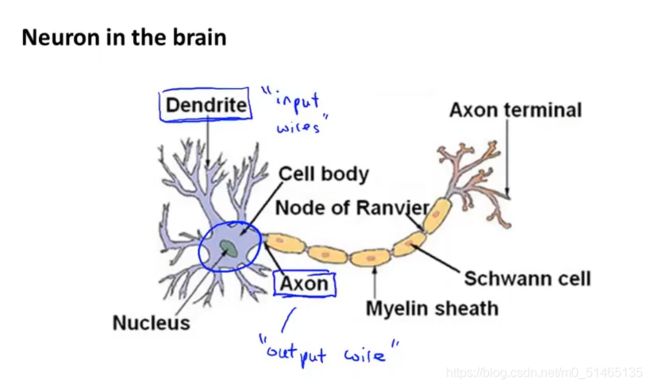神经元之间利用微弱的电流进行沟通，也称作动作电位，神经元想要传递一个消息，它就会通过它的轴突发送一段微弱电流给其他神经元，这是人类思考的过程，神经元把收到的信息进行计算并且向其他神经元传递信息。
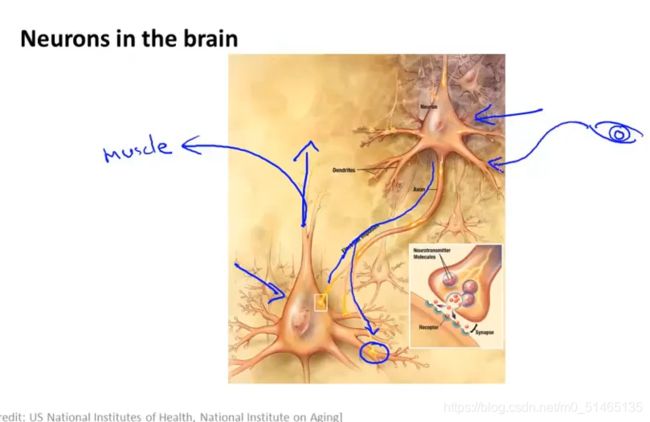在单个神经元中，如下一个简单的模型来模拟神经元的工作，将神经元模拟成一个逻辑单元，黄色圈圈类似于神经元的细胞体，通过树突传递给它信息，然后神经元进行计算，并且通过它的输出通道（轴突）输出计算结果。
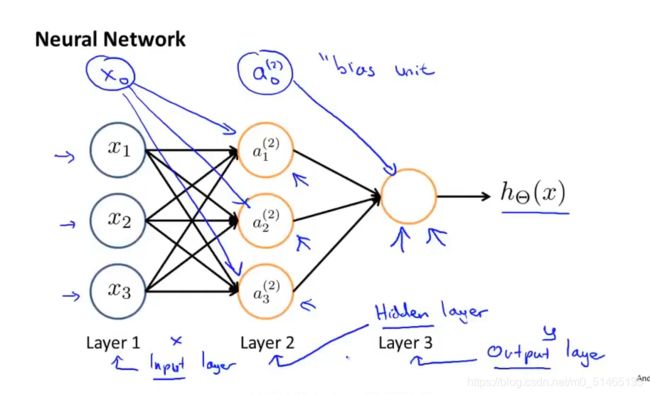
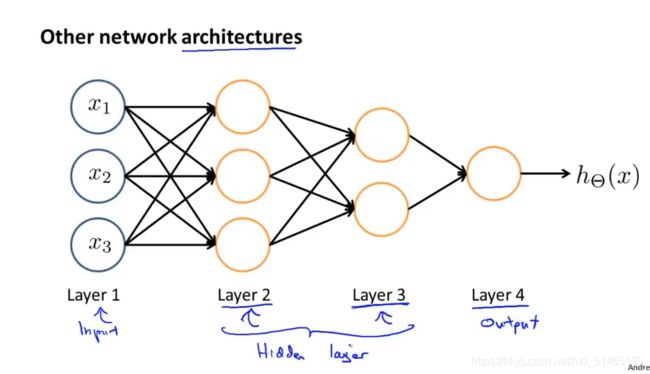
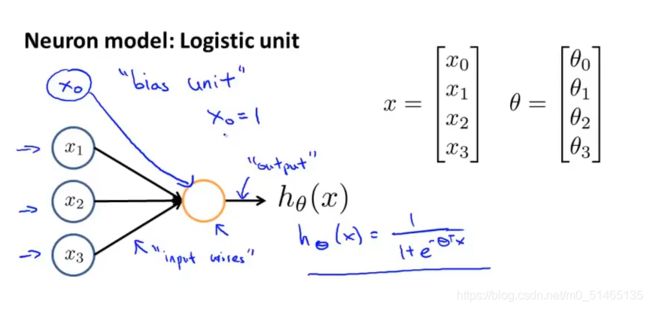神经网络就是一组神经元连接在一起的集合，主要分为三层输入层、隐藏层、输出层。

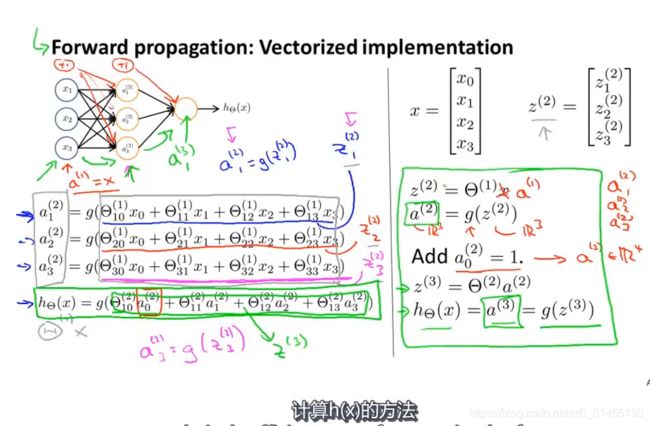
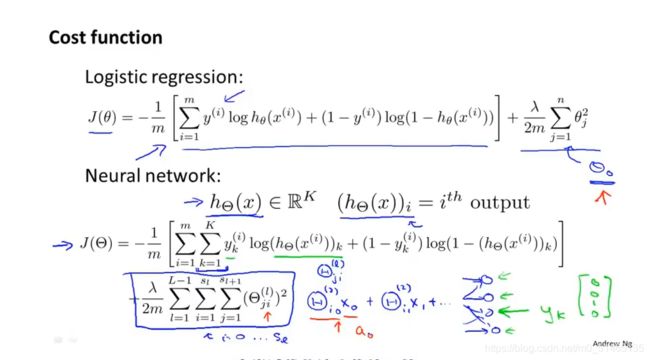
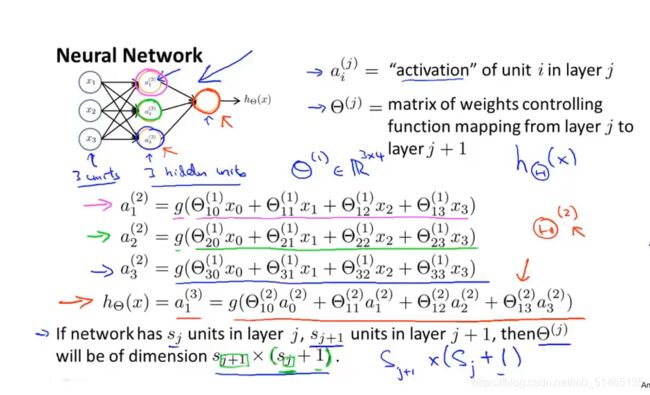
神经网络具体的计算步骤，ai^(j)表示第j层第i个神经元的激活项，激活值是指由多个具体神经元接收到的带有权重矩阵连接的输入信号。θ ^(j)为3×4的权重矩阵，它控制从某一层到另一层的映射。下图给出隐藏单元ai ^(j)计算步骤。如果一个网络在第j层有Sj个单元，在第j+1层有Sj+1个单元，那么矩阵θ ^(j)，即控制第j层到第j+1层映射的矩阵它的维度为Sj+1*（Sj+1)

7.4神经网络模型展示Ⅱ

神经网络架构

7.5例子理解神经网络模型

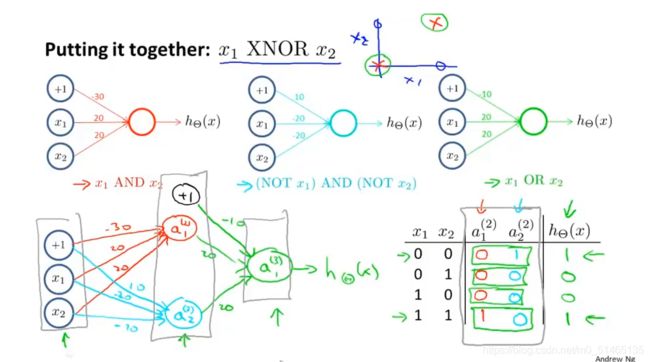
当有x1、x2两个输入特征且是二进制的，左图为样本的简化版本，当我们计算目标函数，（XOR）当两个值恰好一个等于1时，y=1，（XNOR）两个值同时为真或同时为假时，y=1
逻辑与：And function
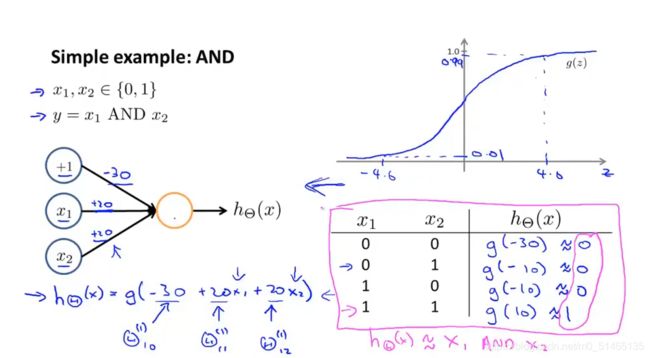逻辑或：OR function
NOT function
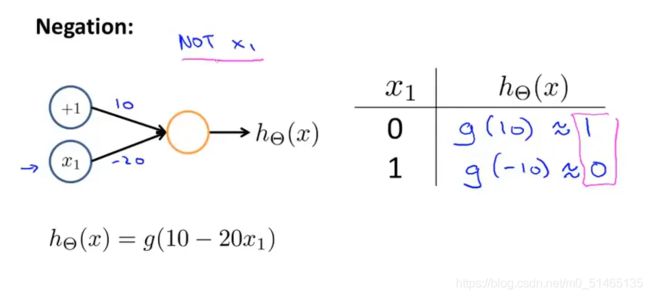XNOR的逻辑
神经网络的应用：识别手写数字

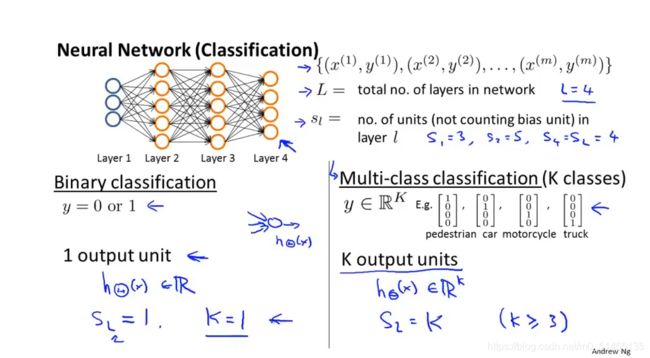
7.6神经网络解决多元分类问题

8.1代价函数（神经网络）

二进制分类和多分类

用于神经网络的代价函数：

8.2反向传播算法

反向传播算法：最小化神经网络代价函数的算法
反向传播算法：
δlj代表了第l层的第j个结点的误差，δ4j也就等于这个单元的激活值减去训练样本里的真实值之差

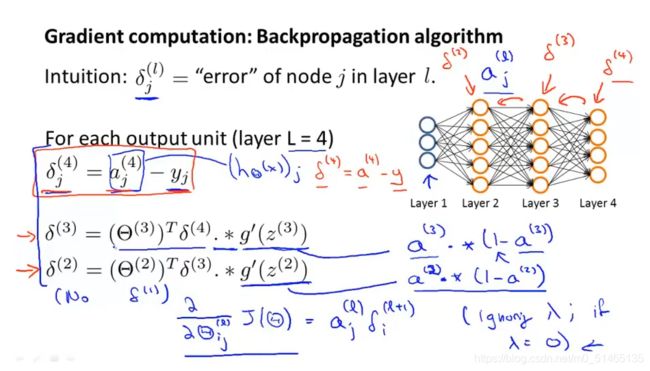
8.3理解反向传播

前向传播的步骤

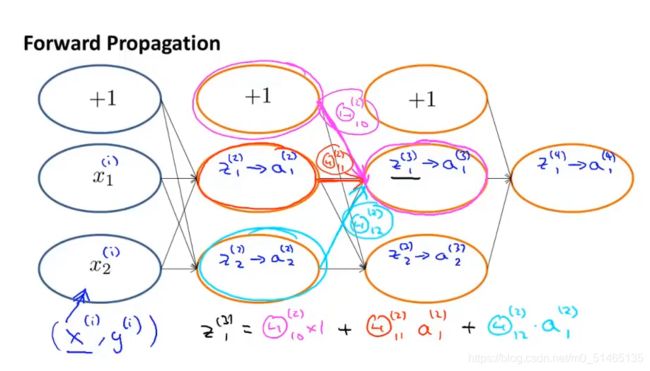当如果输出只有一个输出单元的情况，且忽略正则项，可将代价函数看作是一种方差函数，因此cost(i)可看作预测样本值得准确程度
δlj代表了第l层的第j个结点得到的激活项的误差，准确地说δ项实际是代价函数关于z^(I)_j（代价函数）的偏导数
反向传播过程：

8.4反向传播实现过程，注意：展开参数

8.5梯度检验

反向传播含有很多细节实现起来比较困难，并且有一个不好的特性很容易产生一些bug，当它与梯度下降或与其他算法一同工作时，看起来能够正常工作并且代价函数J(θ）在每次梯度下降的迭代中也在不断减小，但最后得到的神经网络误差高，因此利用一种思想叫做梯度检验，可解决这种问题。因此在神经网络中实现反向传播或者类似梯度下降算法时，都会做梯度检验

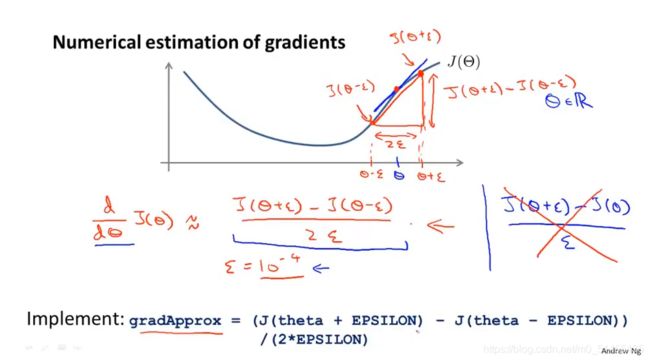
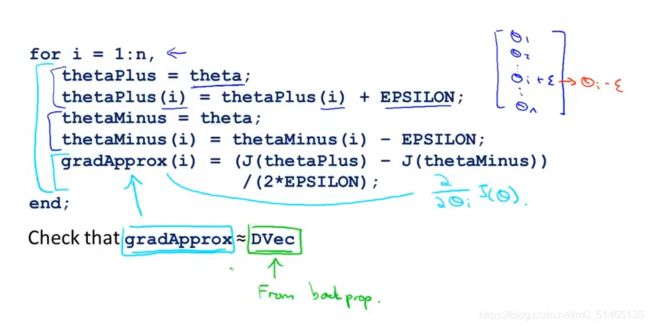
当梯度检验完成后应关闭梯度检验

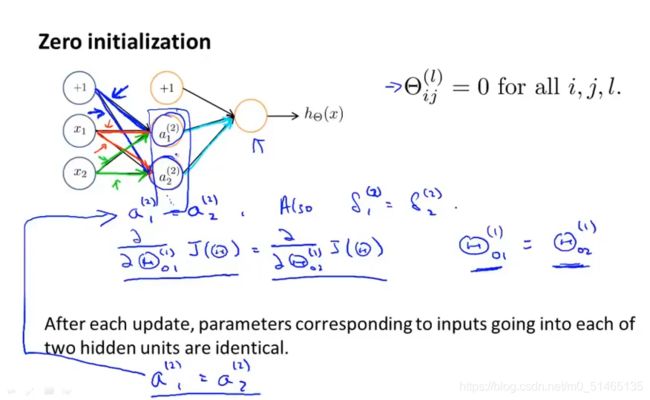
8.7随机变量θ的初始化

8.8神经网络总结

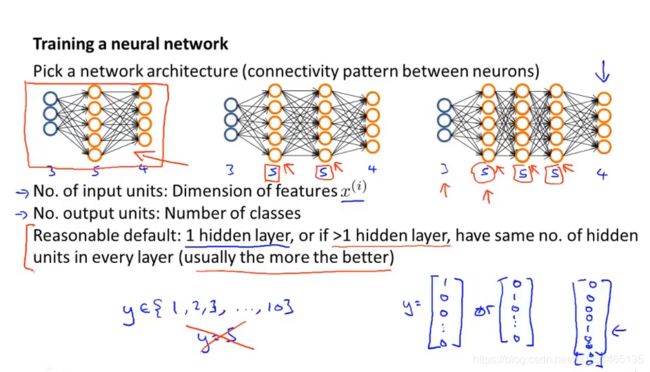
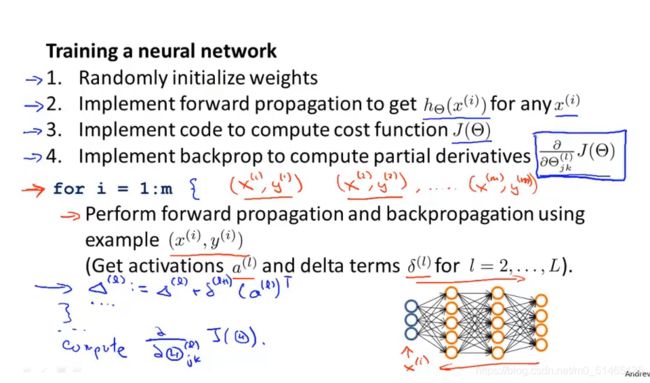
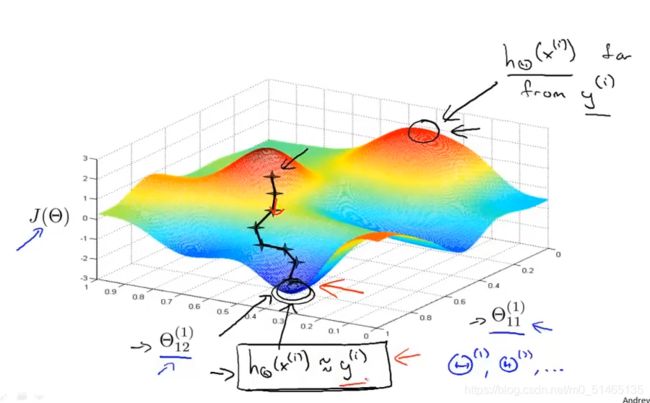
训练一个神经网络：
1.选择神经网络架构（神经元之间连接模式）
2.输入输出单元的选择
3.默认使用单个隐藏层，若不止一个隐藏层的话，则每一个隐藏层通常有相同的单元个数，通常情况下，隐藏层单元越多越好，隐藏层的单元个数≥输入特征数

实现步骤：
1.构建一个神经网络，随机初始化权重
2.执行前向传播算法，也就是任意输入一个x^(i),计算出对应的hθ（x)的值
3.通过编程计算出代价函数
4.执行反向传播算法计算出偏导数项
5.梯度检验来比较计算用反向传播得到的偏导数项与用数值方法得到的估计值进行比较，梯度检验确保两种方法得到基本接近的两个值
6.使用最优化算法，例如梯度下降算法，将优化算法与反向传播算法相结合（反向传播计算出这些偏导数项的值）来最小化关于θ代价函数J(θ）

五、评估学习算法

9.1决定下一步做什么

假设在得到学习参数后，如果将假设函数放到一组新的样本上进行测试，产生了巨大误差，想要改进这个算法，接下来应该做什么？
1.尝试使用更多的训练样本进行训练
2.尝试选用更少的特征（防止过拟合）
3.尝试选用更多的特征（防止欠拟合）
4.增加多项式特征的方法
5.增加或减小正则化参数λ的值

然而选择上面的方法可能会花费大量的时间评估改进算法，下面提供一种方法来评估机器学习算法的性能。

机器学习诊断法：这是一种测试法，通过执行这种测试能够了解算法哪里出现了问题，并且获得指示来提高性能。虽然这些诊断法的执行和实现需要花些时间，但可以节省找算法问题的时间。

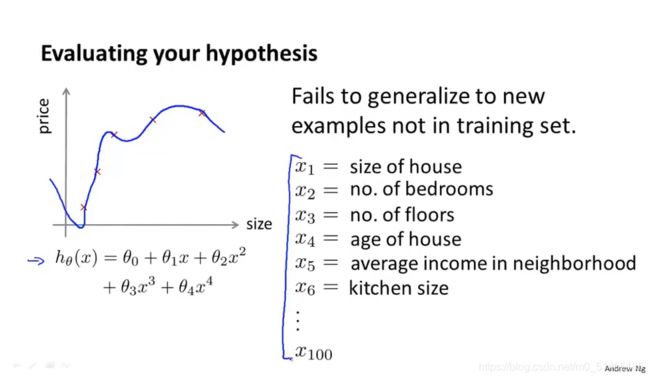
9.2评估假设

怎样评价你的算法？如何防止过拟合欠拟合问题？
首先划分数据集——训练集：测试集=7：3
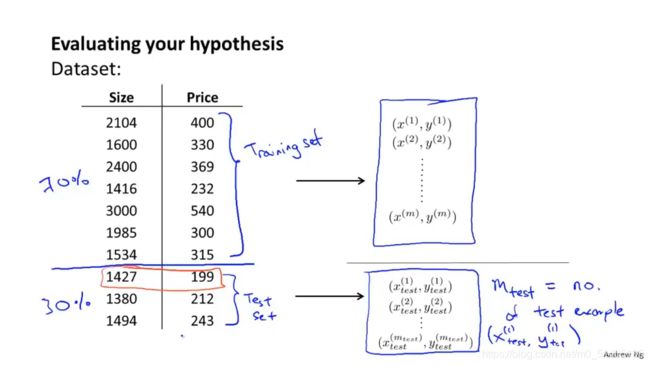线性回归的训练/测试过程：
首先从训练集学习得到参数θ（最小化代价函数），其次计算出测试误差
逻辑回归训练/测试过程

9.3模型选择（训练、验证、测试集）

对于一个数据集怎么选择最合适的多项式次数，怎么选用正确的特征来构造算法，又怎么选择正则化的λ？这类问题叫做模型选择问题
训练集：交叉验证集（cv）：测试集=6：2：2
训练、验证、测试集误差：
模型选择方法：依次选择一个模型，求出该模型的最小化代价函数，得到相应的参数θ，将θ带入交叉验证集的代价函数中，计算出J_cv，来观察这些假设模型在交叉验证集的效果如何，选择交叉验证误差J_cv最小的那个假设作为我们选择的模型

9.4诊断偏差与方差（判断欠拟合与过拟合）

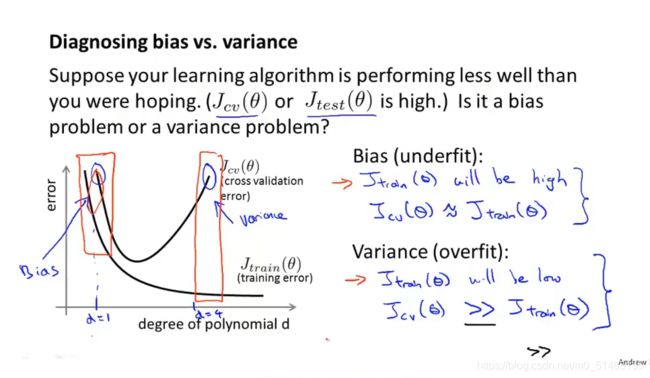
如果算法表现不理想多数是两种可能，要么偏差比较大，要么方差比较大（即欠拟合与过拟合）
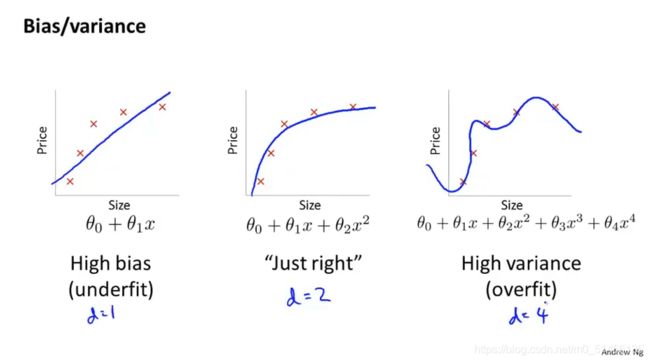
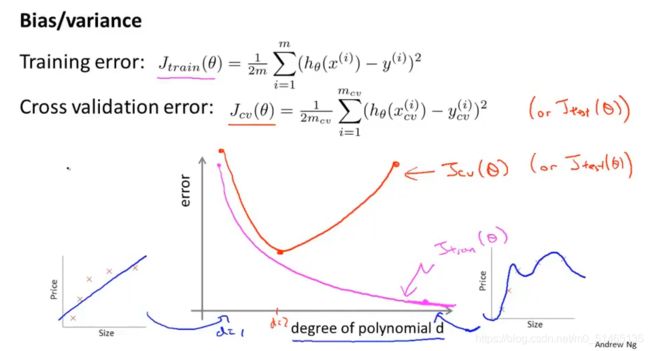区别偏差与方差（欠拟合与过拟合）：当训练集错误与交叉验证集错误同时偏高，则为欠拟合；当训练集错误较低、交叉验证集错误较高，则为过拟合。

9.5正则化和偏差、方差

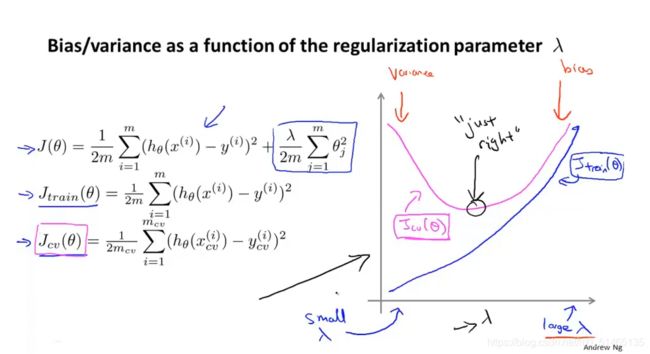
正则化如何影响偏差和方差，正则化参数λ较大时，θ被惩罚得很严重；正则化参数λ较小时，出现过拟合；λ参数正好时对数据拟合比较合理。

如何选择正则项参数？
选取12组假定的λ，分别求出它们的最小化代价函数，并求出相应的θ，并且分别通过交叉验证集的平均误差平方和，选取这12个模型中交叉验证集误差最小的那个模型作为最终选择。最后若想知道该模型的测试误差，可观察它在测试集上的表现。
当正则项参数λ变化时，交叉验证误差和训练误差如何变化？
对于交叉验证误差，当λ过大时出现欠拟合现象，此时为交叉验证集高偏差，当λ取值很小出现过拟合，由于过拟合原因也会使交叉验证集误差很大。
对于训练误差，当λ值较小时，训练集拟合相对较好，λ增大时，训练集误差上升，此时训练集都不能很好的拟合。

9.6学习曲线

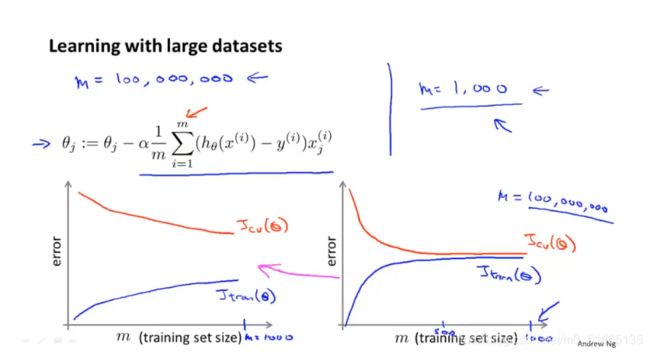
学习曲线是通过画出不同训练集大小时训练集和交叉验证的准确率，可以看到模型在新数据上的表现，进而来判断模型是否方差偏高或偏差过高，以及增大训练集是否可以减小过拟合。

随着训练集容量的增大，平均训练误差在增大；当训练集容量较小时，交叉验证集泛化能力较差，不能很好的适应新样本，当使用更大的训练集时能够更好的适应新样本，因此验证集误差随着训练样本容量m的增大而减小，越能获得更好的泛化表现。
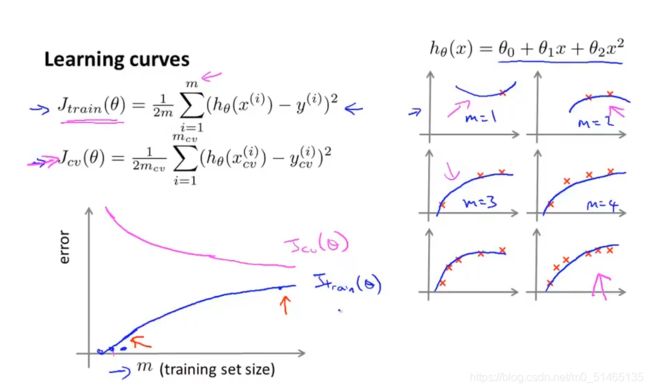高偏差情形时学习曲线的大致走向：
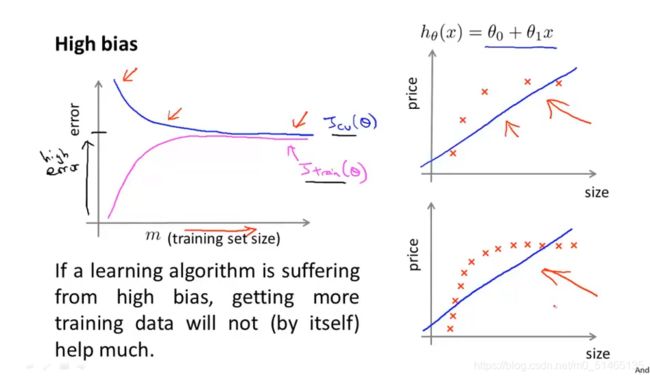高方差情形时学习曲线的大致走向：

六、改进学习算法

10.1决定接下来做什么

假设试图用正则化的线性回归拟合模型，发现并没有达到预期效果，并提出以下选择，那么如何判断哪些方法有效呢？
下图为解决欠拟合与过拟合（high bias、high variance）问题的解决方法：
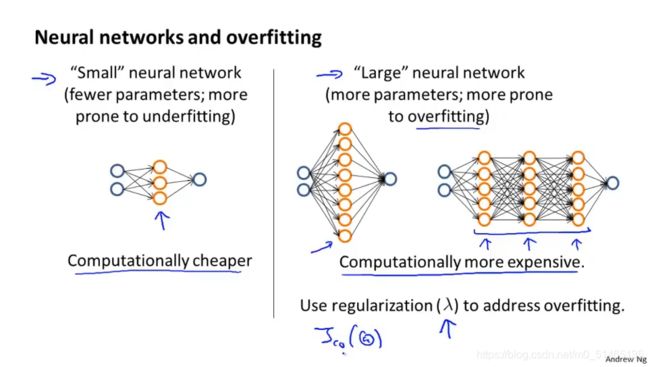
当进行神经网络拟合的时候，一个相对比较简单的神经网络模型（隐含单元比较少），这样的神经网络模型参数较少，容易出现欠拟合，但这种比较小型的神经网络最大优势在于计算量小；与之相对的拟合较大的神经网络结构，隐含的单元较多或隐藏层较多
更容易出现过拟合，有很大的计算量，可以用正则化修正，通常比简单模型更实用。

10.2确定执行的优先级

机器学习系统设计时可能遇到的一系列不同问题：
在实际工作中应该首先处理哪些问题
例如创建一个邮件分类器并且具有高准确度和低错误率：

10.3误差分析

推荐机器学习的方法：首先先快速实现一个简单粗暴的算法，并找出这种算法最难以分类的样本，因为对于不同的算法，对于造成困难的样本总是相似的，并集中处理这些难以分类的样本；最后在改进算法的时候，如果你的算法能够返回一个数值评价指标，来估计计算执行的效果，将会很有帮助

10.4误差评估（偏斜类样本）

例如癌症分类问题，训练一个逻辑回归模型，假设用测试集检验了这个分类模型，并且发现它只有1%的错误（99%正确判断），但是在测试集中只有0.5%的患者真正得了癌症，意味着正类与反类样本数量相差很大，称为偏斜类。

因此当遇到偏斜类样本时，希望得到一个不同的误差度量值（评估度量值），其中一种叫做查准率和召回率（查全率）。
查准率:在所有预测阳性中，评估预测的准确性
召回率（查全率）：在真实阳性中有多大比率被我们正确的预测

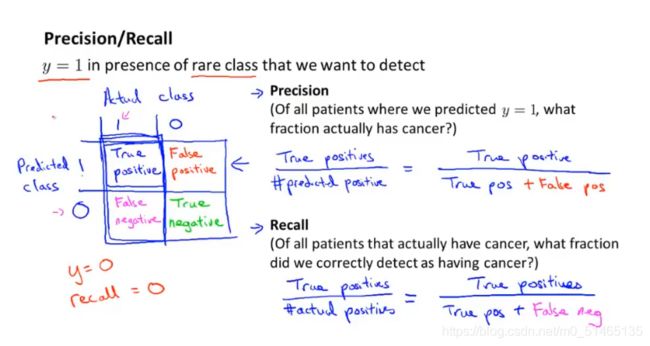
10.5查准率和查全率的权衡

当不断提升预测值y=1时的θ取值范围，查准率就会提高，反而查全率降低，因为在最有把握的癌症病例中预测，会漏掉一些癌症病例；当降低预测值y=1的取值范围，查全率就会提高，准确率降低。
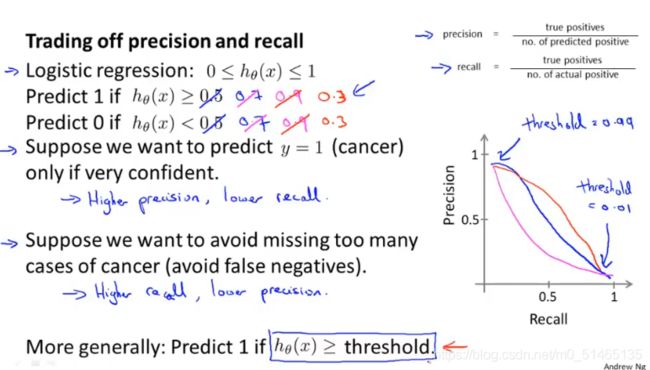如何自动的选取临界值，怎样决定哪一个算法是最好的？
有一种结合查全率和查准率的方式F，通过F值来选择算法，理想化完美的算法F值为1

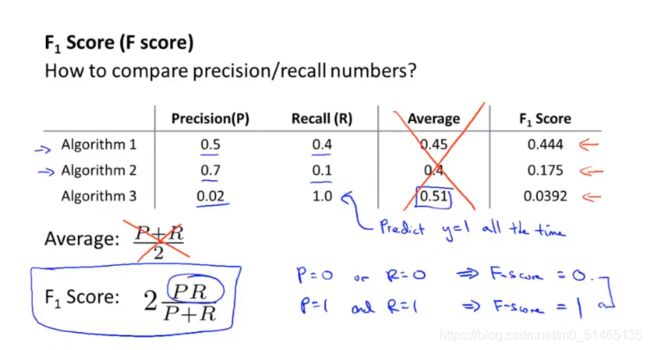
10.6机器学习数据

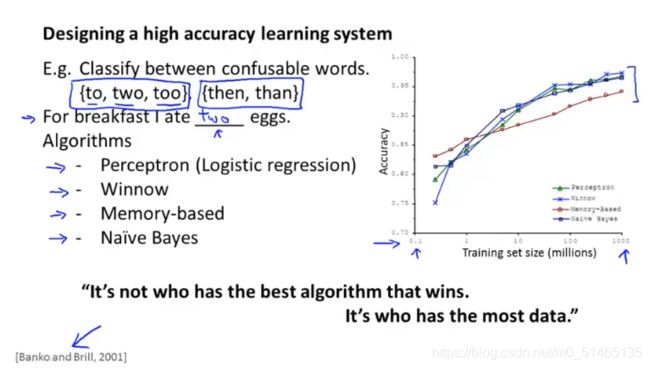
如果有大量的数据而且训练了一种带有很多参数的学习算法，那么这将得到一个高性能的学习算法

七、认识SVM

11.1SVM算法的代价函数

很多监督学习算法的性能都非常相似，所以要考虑的大多并不是选择哪一个算法，而是更多的去想构造这些算法时所使用的数据量。

首先用另一种观念看逻辑回归
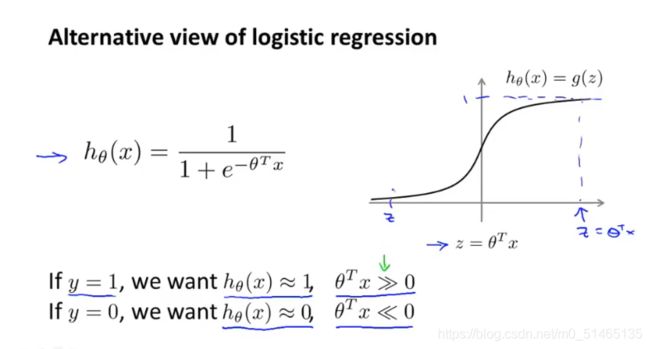观察逻辑回归的代价函数，定义紫红色的曲线（cost1z、cost0z）和逻辑回归中代价函数的形状很相似
有了以上定义，开始构建支持向量机，在逻辑回归中代价函数的前项和正则项，通过设定不同的正则化参数λ以便能够权衡在多大程度适应训练集，但对于SVM而言，而是用一个不同的参数C，来最小化CA+B

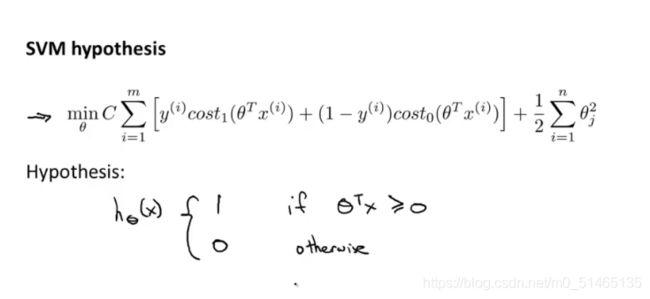
11.2直观上对SVM的理解

如果C非常大，那么在最小化代价函数时，希望第一项为0
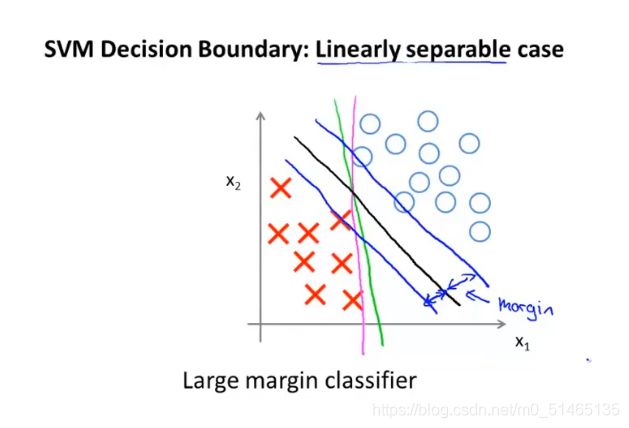
支持向量机也称为大间距分类器，下图中黑色的线与样本的距离最大，这个距离叫做支持向量机的间距，这使得支持向量机有鲁棒性，因为它在分离数据时会用最大的间距去分离
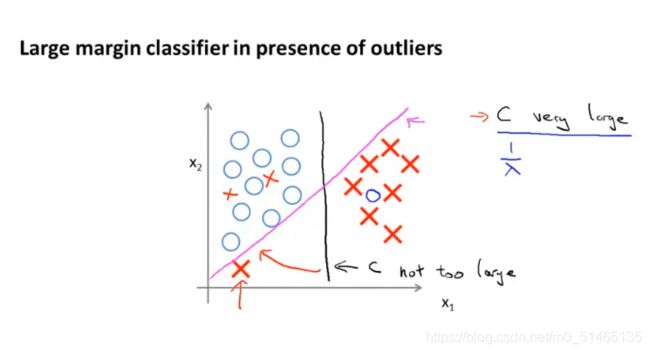
当C非常大的时候能够产生类似紫红色的决策边界，而当实际应用支持向量机C并不是很大，它可以忽略异常点来得到正确结果

11.3SVM的数学原理

复习向量内积的性质：
几何意义：向量v在向量u的投影长度P与向量模的乘积，特别地，u,v之间的夹角大于九十度则p为负值。
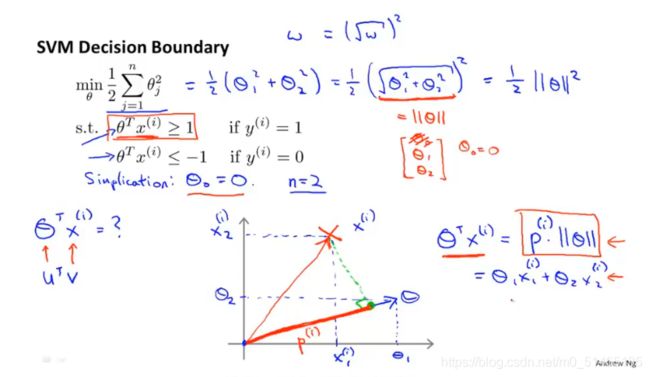
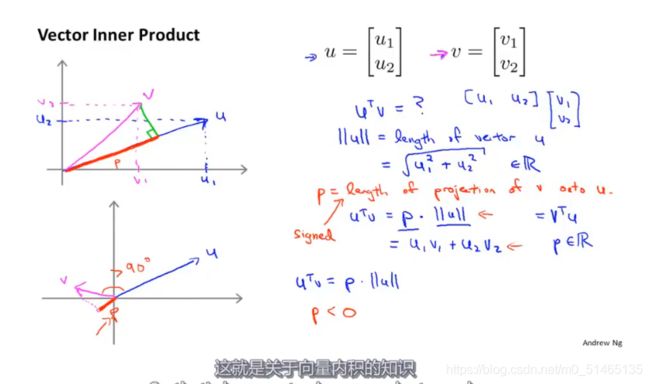若不考虑第一项，则假设代价函数的第一项为0，特征数n=2
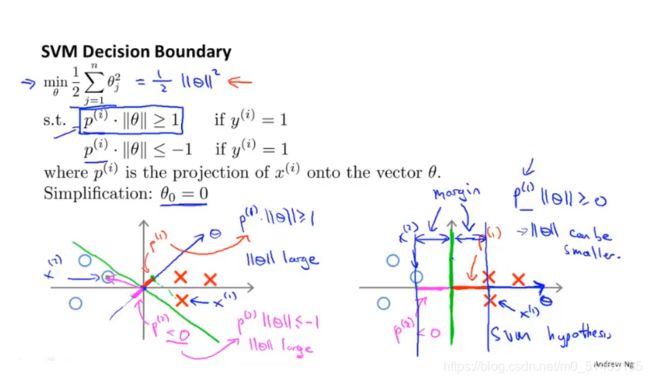
假设选左图这个决策边界，但决策边界距离训练样本很近，这不是一个好的选择，因为第一项θ^Tx=0时,参数向量θ与决策边界90度正交，考虑样本xi到θ的投影p,当p模很小时，要想pθ乘积的模很大，则必须θ的模很大
要想逐步优化目标函数，即最小化θ的模，因此对参数θ而言，选择一个间距很大的决策边界（p值很大），如右图所示，这就SVM为什么会产生大间距的原因

11.4什么是核函数

非线性决策边界
高阶的多项式运算量非常大，是否可以有不同的或者更好的特征的选择，可以用来嵌入到假设函数中——可以构造新特征f1,f2…的方法
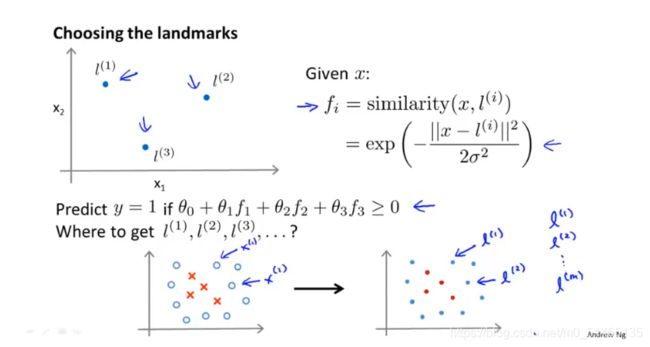
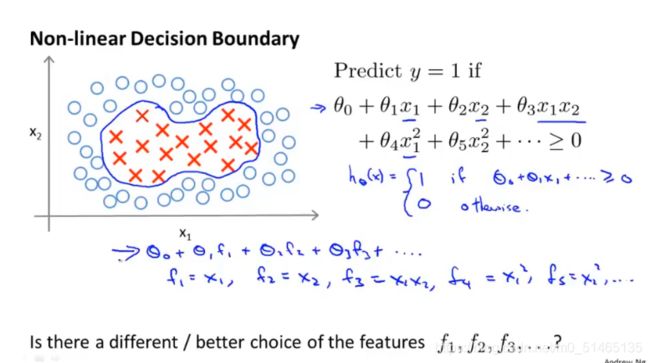假设只对于特征x1，x2，手动选取一些点，称这些标记点为l1，l2, l3，将特征f定义为一种相似度的度量，即度量样本x与第i个标记点的相似度，相似度函数就是一个核函数（高斯核函数）
当特征x与标记点l很相近，则特征f非常接近于1；当特征x与标记点l距离非常远，则f会接近于0
预测函数如何给出预测结果（构建非线性边界）？
当给定θ，由特征x得到特征f，若θ0+θ1f1+θ2f2+θ3f3≥0，那么预测值为1，则说明该点非常接近标记点l，最后得到判定边界。

11.5核函数如何作用

支持向量机如何通过核函数来有效的学习复杂非线性函数？

列出该过程的大纲：给定m个训练样本，选取与m个训练样本完全一样的位置作为标记点。对于给定样本x，来计算特征f，将f合并写作一个特征向量；对于训练样本，将m个特征合并为一个特征向量。
所以当给定核函数和相似度函数后，如何使用简单的支持向量机进行预测？
已知θ的预测过程：假设已经学习到了参数θ，再给定x的值，并对样本x做出预测，先要计算特征向量f，当θ^Tf≥0时，预测y=1。
未知θ的预测过程：使用SVM最小化代价函数的方法得到参数。
SVM参数的分析
C大意味着λ小，进一步说明正则项的影响较小，可能得到一个低偏差高方差的模型； C小意味着λ大，说明正则项影响较大，可能得到一个高偏差低方差的模型。
σ^2偏大时，对应的相似度函数相对光滑，这会给模型带来高偏差低方差；反之，相似度函数变化剧烈，对应的模型低偏差高方差。

11.6使用SVM

其他核函数的选择
逻辑回归、SVM、神经网络算法的比较

八、无监督学习

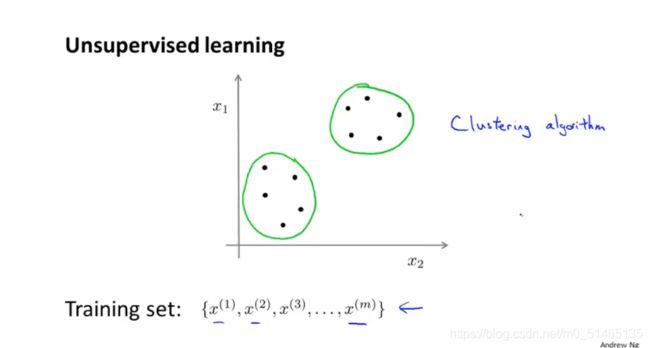
12.1聚类算法

监督学习带有标签，即有正负样本，然后用假设函数去拟合它

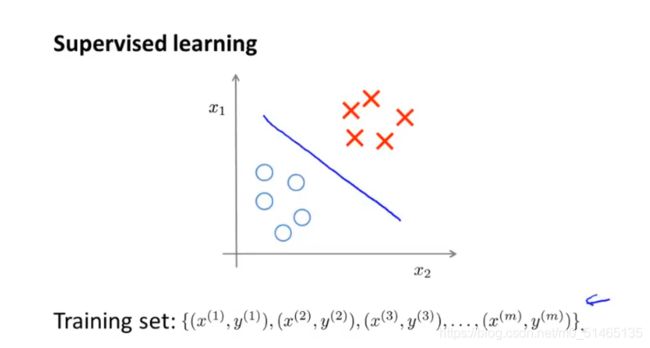在无监督学习中数据并不带有任何标签信息，但从样本中可以分成若干组分开的簇，这种能找出簇的算法，被称为聚类算法

聚类算法的应用

12.2K-Means算法

假设有如下一个无标签的数据集，并且想将其分为两个簇，具体操作如下，首先随机生成两个点，这两点叫做聚类中心。k均值算法是一个迭代算法，它会做两件事情，第一个是簇分配，第二个是移动聚类中心。

簇分配：每次内循环的第一步是要进行簇分配，也就是将图上每个点与红色聚类中心更近还是与蓝色聚类中心更近，将每个数据点分配给两个聚类中心之一。
移动聚类中心：将聚类中心移动到同色点的均值处。
重复上述过程，最终K均值聚合了
①生成聚类中心

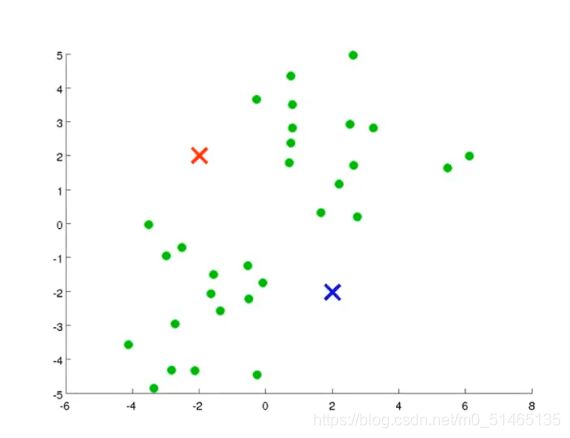
②进行簇分配、移动聚类中心
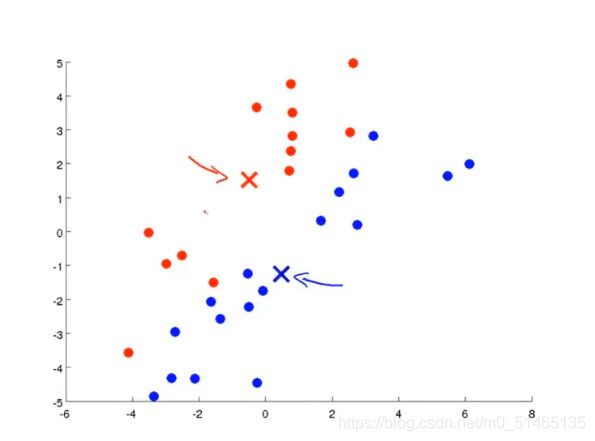③再次检查无标签样本与红色还是蓝色聚类中心更近，并将其变为红色或蓝色
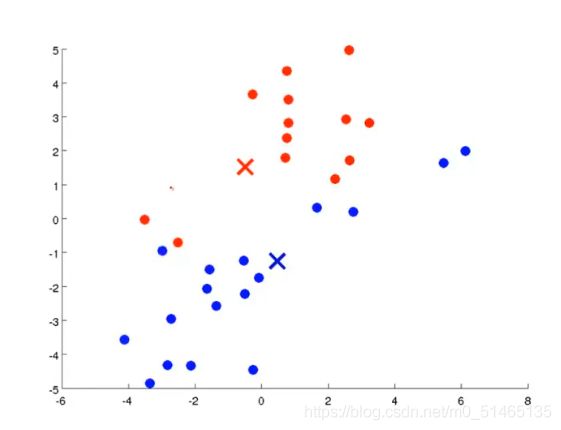④再次移动聚类中心
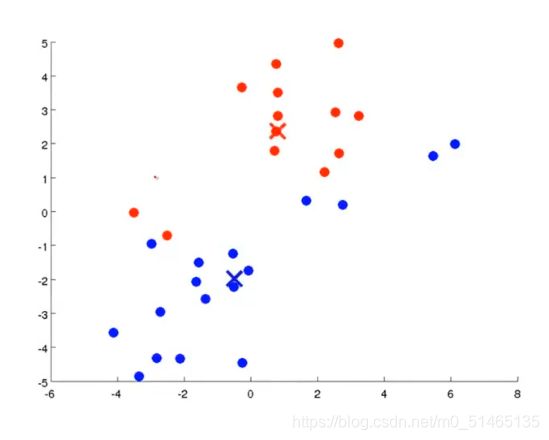⑤重复上述过程

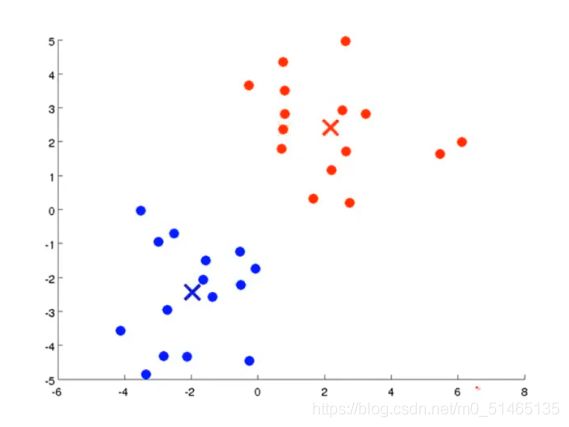K均值算法：
K均值算法接收两个输入，一个是参数K（它表示想从数据中聚类出簇的个数），另一个是一系列无标签的训练集
首先初始化聚类中心μ1，μ2…μK，
簇分配步骤：找到一个聚类中心，使得|xi-uk|的值最小，该k值就是赋给ci的值。即样本xi分为ci类
移动聚类中心：对于每一个聚类中心（从k=1~K),μk就等于簇中所有点的均值

12.3K-Means的代价函数（优化目标）

K-Means代价函数又被叫做失真函数。

ci表示x样本的分类序号；μk表示聚类中心的位置（K表示聚类数量，k表示聚类中心的下标）；μci表示xi所属的那个簇的聚类中心；K均值算法的代价函数J要做的事情就是找到ci和μi使得能够最小化J
簇分配实际是找出最小化代价函数中的参数ci，移动聚类中心实际是找出最小化代价函数中的参数uk，然后继续迭代。

12.4K-Means的随机初始化

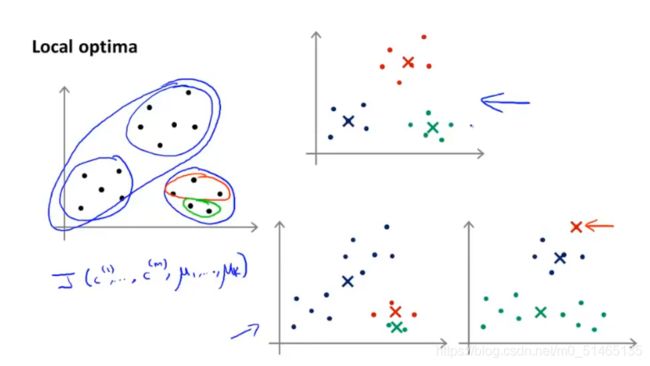
如何初始化k均值聚类算法的聚类中心u？如何使算法避开局部最优？
初始化聚类中心步骤：当运行k均值算法时，应该把聚类中心的数值K设置为比训练样本数量m小的值，接着随机挑选k个训练样本，然后设定μ1到μk等同于这k个样本
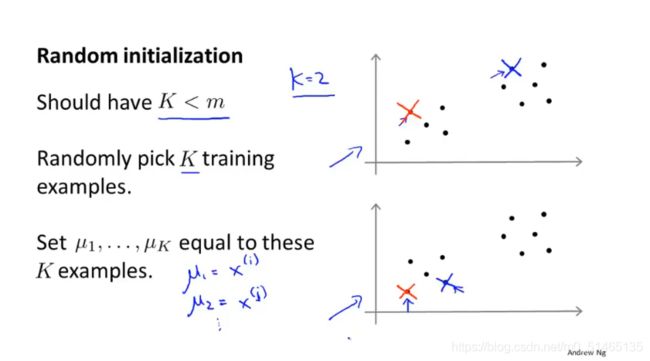k均值算法可能存在局部最优

12.5K-Means中如何选取聚类数量

目前为止用来决定聚类数量最常用的方法还是利用可视化图或者聚类算法的输出

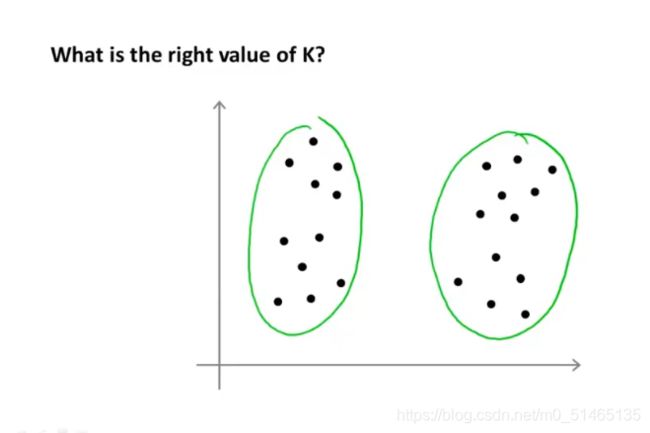
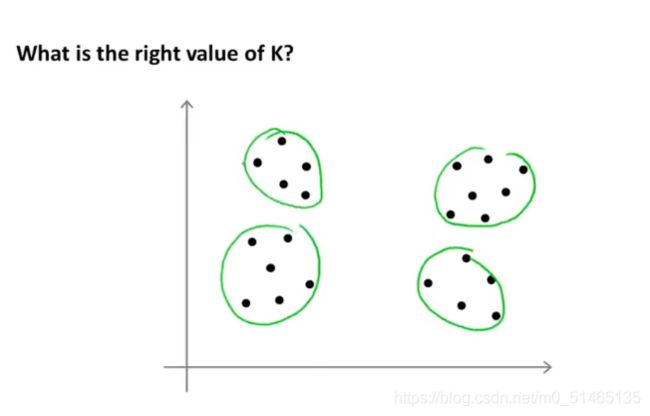选择K值时的方法：
1.“肘部法则”，改变K值观测代价函数J，当图形出现“肘部”（拐点），也就说明在该位置为最佳聚类数，但在平滑曲线该方法不适用。
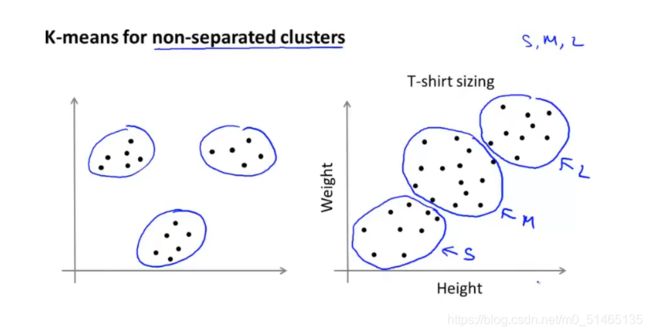
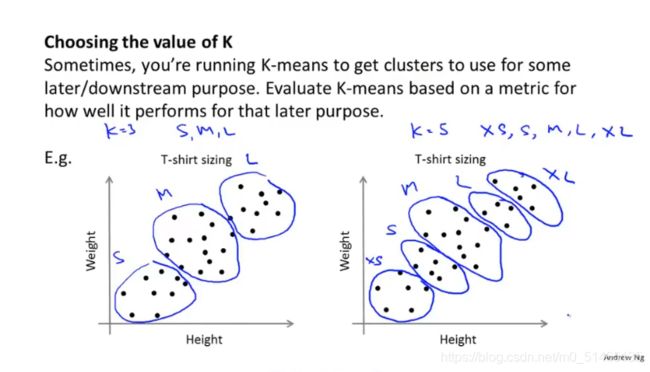
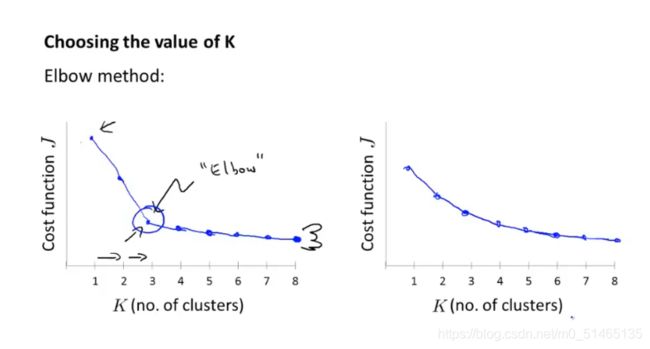2.通常使用k均值聚类是为了得到一些聚类用于后面的目的，举例：T恤尺寸的分类是否很好的满足顾客的需求？

九、降维

13.1数据压缩（降维的第一个应用）

假设一个数据集有许多特征，且有高度冗余的特征，例如厘米与英尺就是两个高度冗余的特征。

2D to 1D :通过把这些样本投影到同一直线上，这就是对原始数据的一种降维。
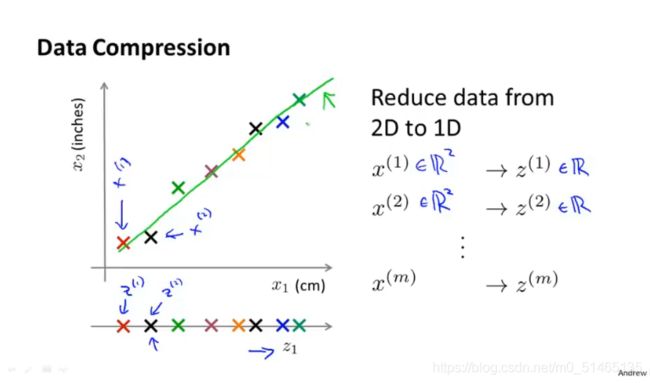3D to 2D:将三维上的数据投影到二维平面

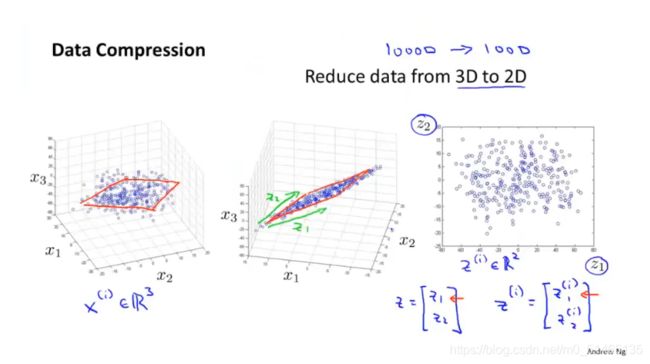
13.2数据可视化（降维的第二个应用）

假设有一个大的统计数据集，如何可视化这些数据？
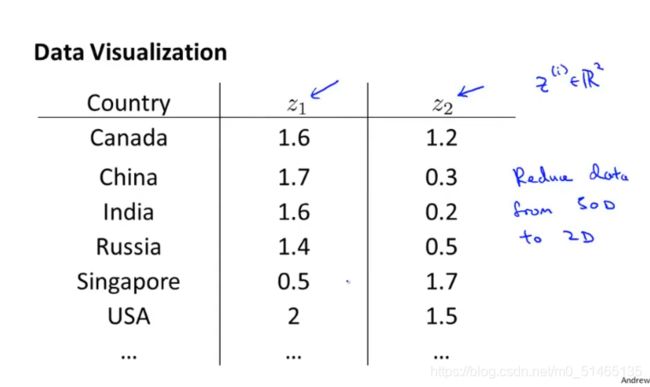
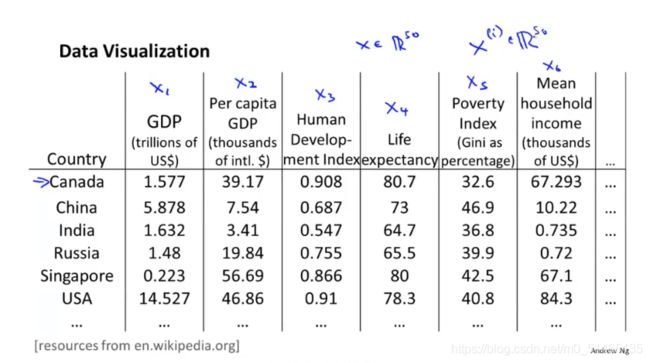利用降维的方法，用两个特征向量z代替多个特征x，并将它们在二维平面上表示出来，但它们不是直接合适的物理特征，需要了解这些特征大致意味着什么

13.3什么是主成分分析（PCA）

对于降维问题，最流行的算法叫做主成分分析法（PCA）

假设对如下数据集降维，即找到一个投影直线，将二维降为一维。PCA就是找到一个更低维的平面，然后将数据投影在上面，并且优化使得数据点到投影后的点之间的距离最小（投影误差最小）。因此在应用PCA之前先进行均值归一化和特征规范化,使x1,x2其均值为0。
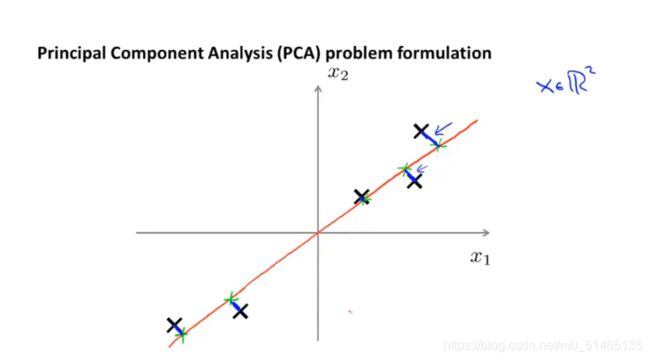如果将数据从二维降到一维，PCA要做的是试着找一个向量ui，进行数据投影后能够最小化投影误差的方向；进而在n维数据中，则不只是想找单个向量来对数据进行投影，而是寻找k个方向，在这k个向量展开的线性子空间上来对数据进行投影，来最小化投影误差
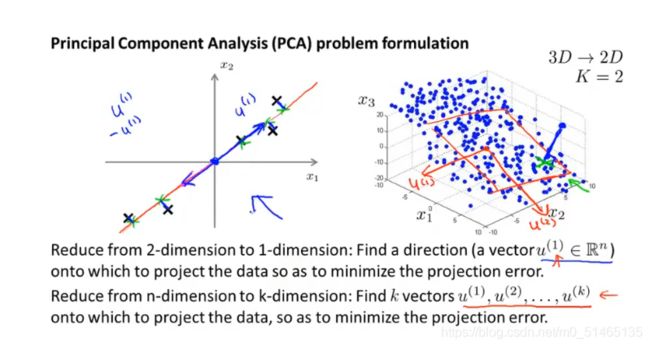PCA不是线性回归——在线性回归中，是最小化点和直线之间的平方误差；在PCA中，是
最小化正交距离，即点与直线的最短距离

13.4如何使用主成分分析法

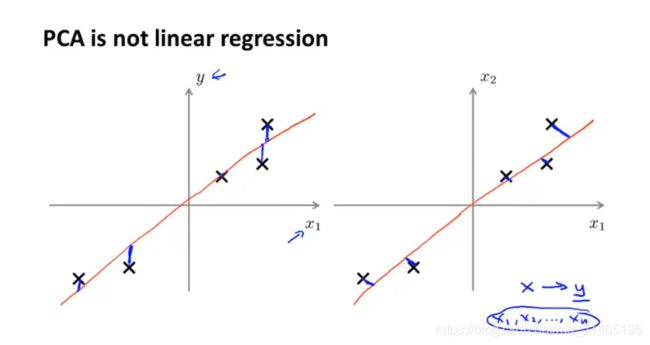
第一步先进行数据预处理（特征缩放/均值归一化：取数据的均值ui，将数据x用x-ui代替，使得数据的均值为零），接下来，如果不同的特征有不同的缩放，则缩放每一个特征到一个相对的价值范围
PCA的数学推导——如何找到你想要的u(i)的值
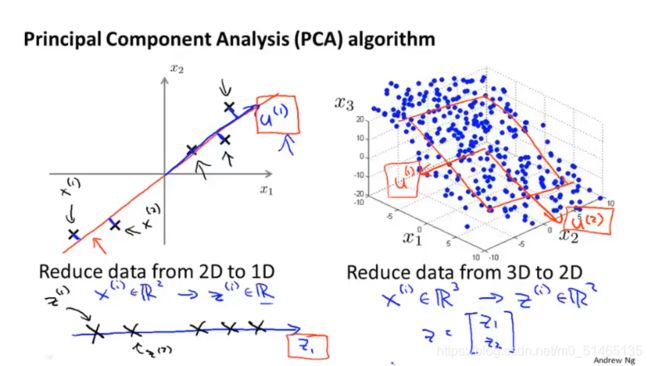要想使n维降低到k维，首先计算协方差矩阵，用SVD函数计算出协方差矩阵的特征向量，取前k个向量，这给了我们k个方向，即投影数据的方向
第二步计算sigma矩阵，利用SVD函数计算出协方差矩阵的向量化，然后得到要降维度矩阵U的前k列，最终定义了如何从一个特征向量x降维到z的表示

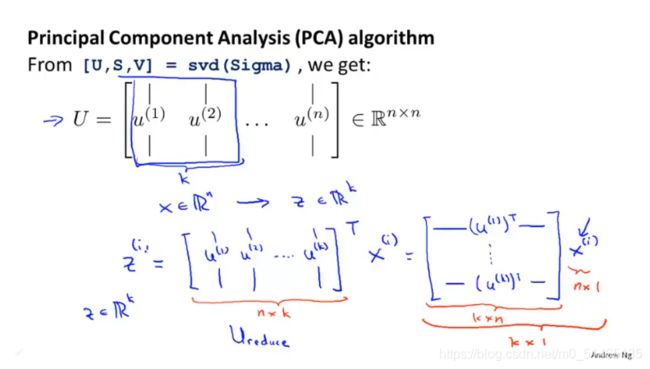
13.5主成分数量k的选择

在PCA中，我们把n维特征压缩为k维，这个k同样被称作数据主要成分保留数量，那么如何选择PCA算法中的k？
均方投影误差和数据总变化的计算方法；
选择k的值来最小化下式以至于小于等于0.01，换一种说法就是选的k能使得百分之99的方差被保留下来
从k=1开始，使用PCA计算这些值，检查不等式是否成立，若不成立k就换成2以此类推，选择最小的能够满足不等式的k，由此可见算法效率不高，好在svd分解会让这事儿好算很多。svd计算过程中，还给出一个对角矩阵S；对于k而言，只要判断右边的式子是不是小于0.01就可以了
总结：先求Svd分解，选择满足下面不等式的最小k值

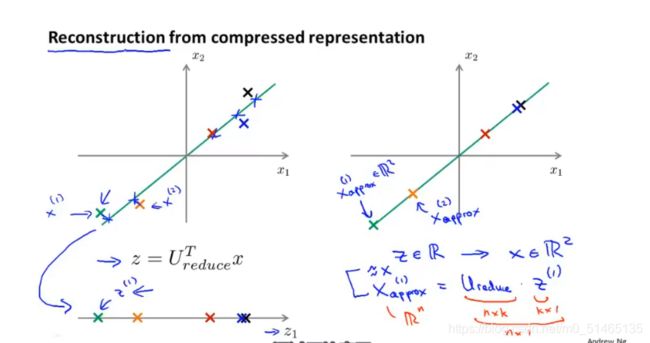
13.6PCA的压缩重现（原始数据重构）

13.7如何应用PCA

监督学习加速算法：对于监督学习，假设选取特征x进行降维，在进行PCA降维时应在训练集上运行，不能用在交叉验证集和测试集，在定义x到z的映射后，可将这个映射到交叉验证集和测试集中
PCA的应用：加快算法运算速度，压缩数据，节省内存，可视化。
用PCA防止过拟合是错误使用，而正则化的方法防止过拟合效果会更好。
通常人们在做机器学习系统时会列如下清单，但是没有使用PCA情况会怎么样？
建议：在实现PCA之前，首先使用最原始的数据来直接做你想做的事，只有当这么做不能达到目的的情况下，才考虑使用PCA。

十、异常检测问题

14.1问题动机

举例飞机引擎的异常特征：
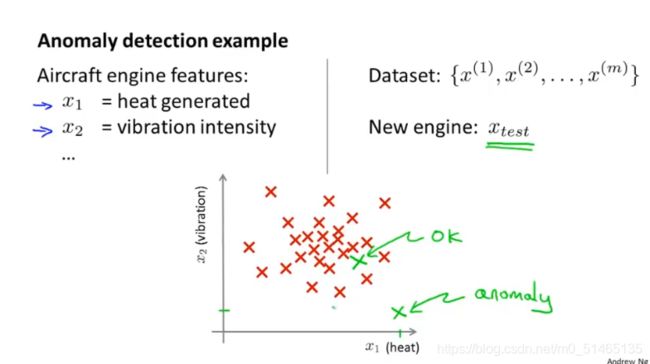建立一个概率模型p(x),当某点出现的概率小于ε则为异常点，某点出现的概率大于ε则为正常点
异常检测算法应用的例子：
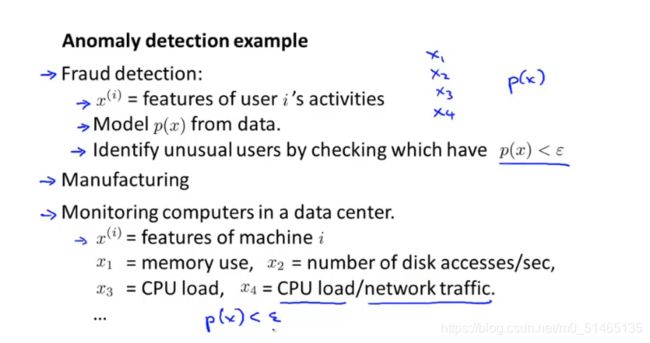
1.例如x为网站用户的行为活动，x1为用户登录的频率，x2为用户交易次数，x3用户发帖次数。。。根据这些数据特征建立模型p(x)，用它来识别网站上行为奇怪的用户。
2.飞机引擎问题，可以找到异常的引擎进一步细察这些引擎的质量。
3.数据中心的计算机监控。

14.2复习高斯分布（正态分布）

其中标准差σ决定了高斯分布概率密度函数的宽度
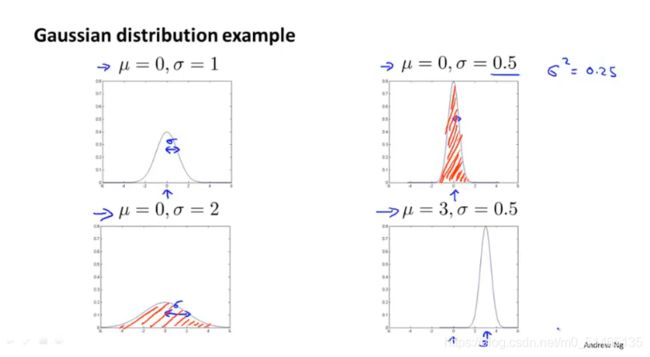
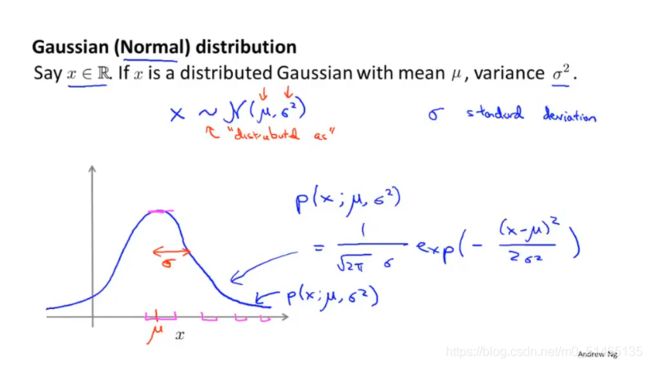高斯分布的例子：因为概率密度函数的面积为1，所以当标准差变小时，概率密度函数会变成“瘦高”，当标准差变大时，概率密度函数会变成“矮胖”。改变μ，将改变概率密度函数的中心。
当给定数据集时μ、σ的参数估计公式——μ为m个样本的平均值，σ^2为所有样本减去平均值的平方再求和。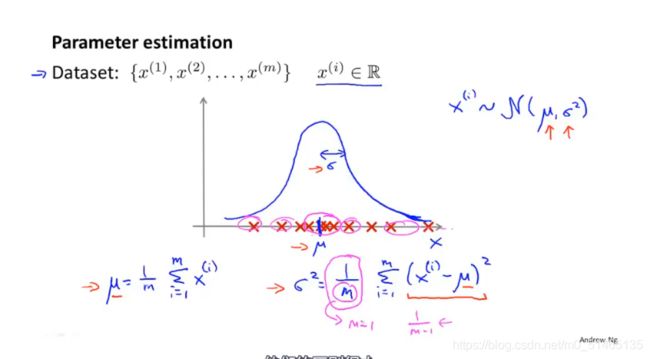

14.3用高斯分布推导异常检测算法

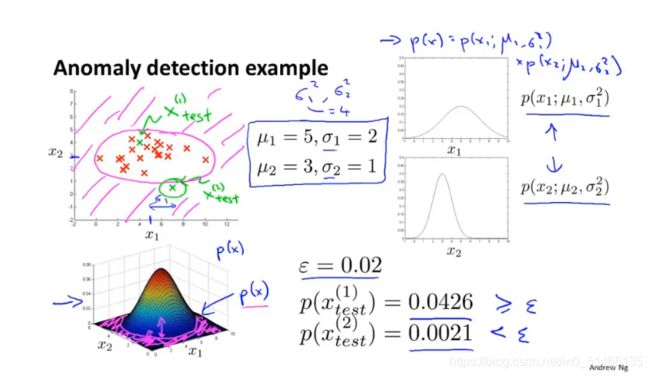
假设特征x无关，p(x)用来估计特征的概率高低，且满足某个高斯分布
☆异常检测算法：第一步选择你认为的异常特征值，第二步找到特征值的平均值μ，求出标准差，第三步：当给定新样本时，计算p(x)的值，如果p(x)的值非常小，则将这一项标注为异常。

14.4开发和评估异常检测系统

飞机引擎的例子：
假如生产出10000个正常的引擎，20个异常的引擎，将其中6000个引擎作为无标签样本来拟合p(x),将剩下的分别设为交叉验证集和测试集中，并且将异常的样本分别放到交叉验证集和
测试集中

14.5异常检测VS监督学习

使用异常检测算法：正常例子数量很少，负样本很多。 经常有不同类型的异常，比如有很多原因导致航空发动机异常，这样将有很少数量的正样本，那么对于一个算法很难从小数量的正样本中去学习异常是什么，以及未来可能出现新的异常，所以要做的是使用大量负样本，让这个算法学到足够多的内容，从那些负样本中学习p(x)的值，并保留小数量的正样本，来评估算法这种情况适用。
使用监督学习算法：有大量的正样本和负样本。有足够数量的样本或者一个已经能识别正样本的算法，假设未来可能出现的正样本与之前训练集中的正样本类似，这种情况下适用，可以观察到大量正负样本学到相应特征，并可以尝试区分正负样本。
异常检测算法适用的例子：1.在欺骗检测中，如果知道人们诈骗时的各种不同的类型，并有一个很小的训练集，对应少量有欺诈行为的用户 2. 引擎制造异常样本少3. 数据中心的机器监视例子。
监督学习算法适用的例子：1.邮件的异常检测2.天气预测3.癌症分类问题有着大量的正负样本。

14.6特征转换以及建立新特征

当应用异常检测时，其中选择使用的特征对运行有很大影响，如何设计或选择异常检测算法的特征？
当数据集出现非高斯特征时，如果使用转换使数据更接近高斯分布的话，算法也许能运行的更好，通常对数据进行一次对数转换，在这么做之后并重新画出直方图，这样就看起来更像高斯分布，这样就能拟合出期望和方差。
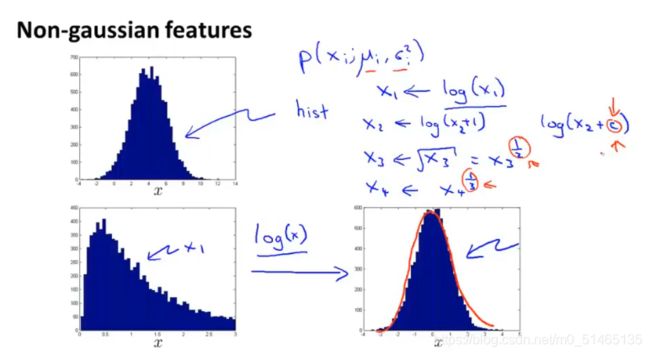
第二件事，如何得到异常检测算法的特征，通常通过一个误差分析步骤，我们希望p(x)的值在正常样本的情况下比较大，在异常样本的情况下比较小。常见的问题是，如果p(x)是可比较的，当样本正常和异常时p(x)都比较大。
下图为假设无标签数据，只有一个特征x1，假设数据拟合出高斯分布，现在假设有一个异常样本，并且这个异常样本x取值为2.5，那么接下来会去看看我的训练样本到底是哪里具体出错了，看看通过这个样本能不能启发想出一个新的特征x2来帮助算法找出异常的样本与剩下正常样本的区别。当重新画数据时，把训练集中的所有正常样本拿出来，就会发现所有的训练样本都是红×了，也希望看到对于异常样本，特征x2能发现不寻常的值，这就是误差分析的过程。
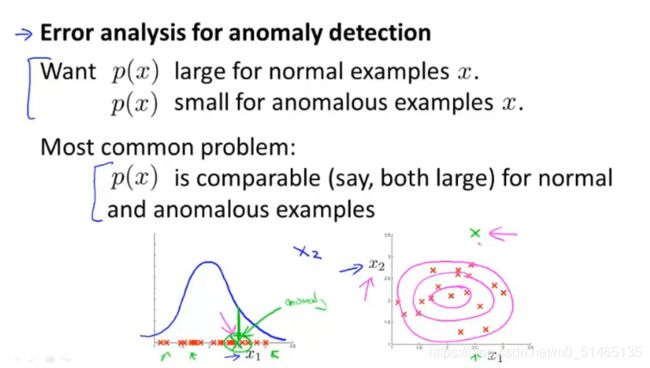平时在为异常检测算法选择特征变量时的一些思考：通常选择特征的方法是选那些既不会特别大也不会特别小的特征，对于那些可能异常的样本，假设在一个数据中心里有很多台电脑，如果想知道哪一台出现故障，如下特征包括占用内存、磁盘每秒访问次数、CPU负载、网络流量等，现在假设某个出错的情况，在我的数据集中CPU负载和网络流量应该互为线性关系，但进入了死机状态CPU负载极具上升，因此可以建立一个新的特征x5，如果一台机器有较大的CPU负载，但是网络流量正常的话，那么将会是一个特征，能够捕捉某种类型的异常情况。也可以创建别的特征x6等等仍然去捕捉机器是否有很高的CPU负载但却没有很高的网络流量这种异常情况。
通过像这种建立特征的方法，就可以捕捉到这些特殊的特征组合所出现的异常值。

14.7多变量高斯分布

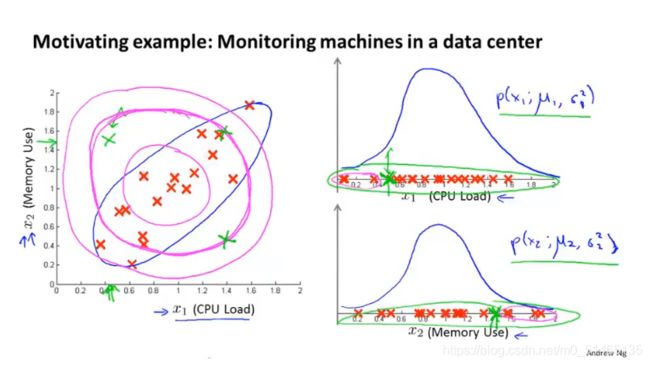改良版的异常检测算法：用到多元高斯分布或者叫做多元正态分布，不要对p(x1)、p(x2)分别建模，而要为所有的p(x)建立一个整体的模型
二元高斯分布的例子，n=2,特征变量x1,x2，如果让μ等于0，对于特定x1x2的值，这个面的高度就是p(x)的值，在这个参数设定下，p(x)在x1和x2都等于0时，取到最高值。当改变一些参数时，Σ协方差矩阵缩小时，它衡量的是方差（特征x1,x2的变化量），结果是鼓包的宽度会减小，高度会增加，相反Σ变大时，方差会相反变化。

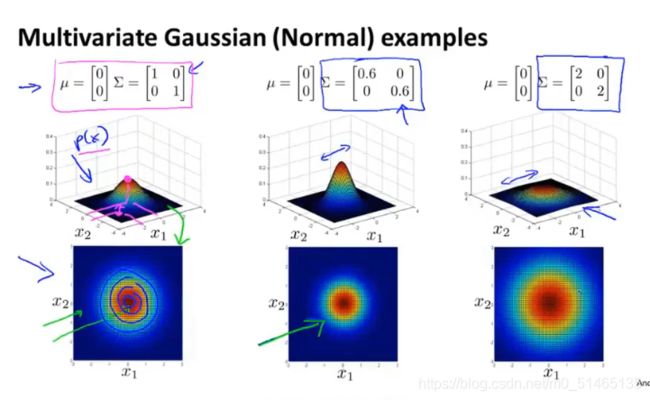当一次改变一个特征变量时;当缩小x1的方差，保持x2特征变量不变，在这个参数设置下，这时x1的方差较小，x2的方差较大。
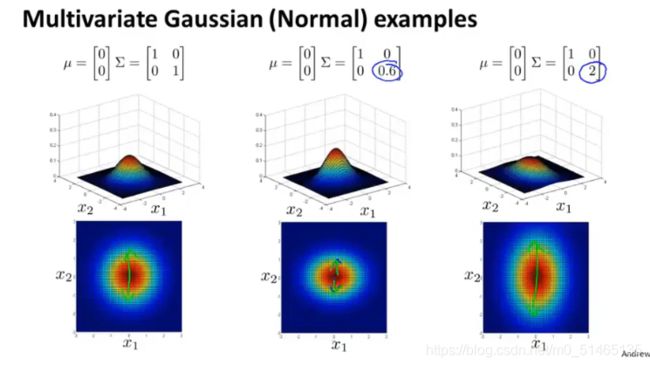给x1x2高度相关的情况建立模型，当改变协方差矩阵非对角线上的元素，会得到一种不同的高斯分布。
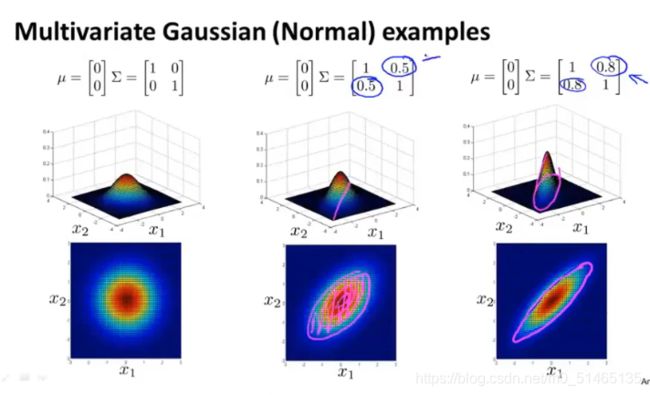
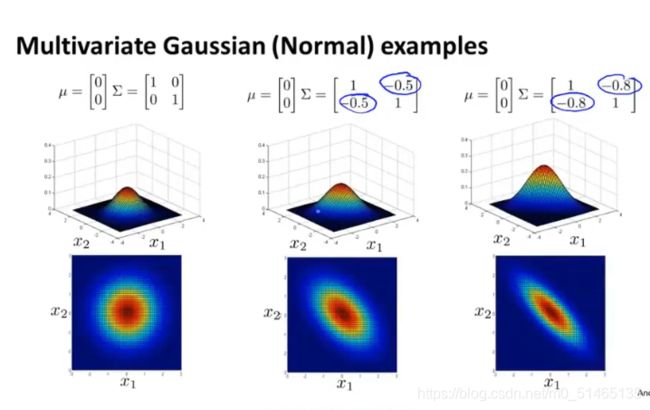当改变μ的值，就会移动整个分布的中心

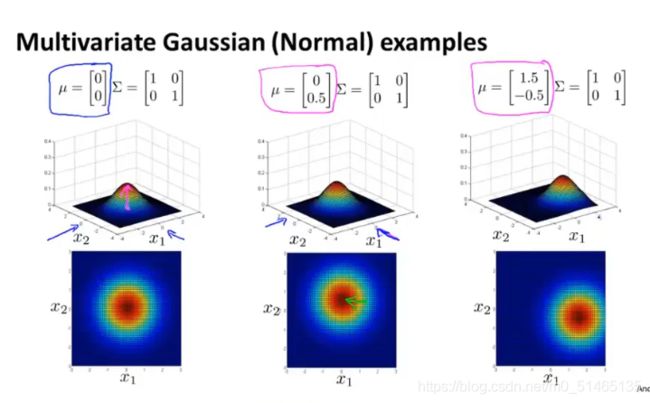
14.8多变量高斯分布的异常检测

回顾多元高斯分布：μ为n维变量，Σ为协方差矩阵，可通过改变μ和Σ来得到范围内一个不同的分布。
参数拟合问题（参数估计问题）：假设一组样本x1到xm，这里的样本都是n维向量，并且样本服从多元高斯分布，那么在给定数据集后如何估计参数μ和Σ？
估计参数有一个标准公式如下，所以只需代入公式就能估计参数μ和Σ
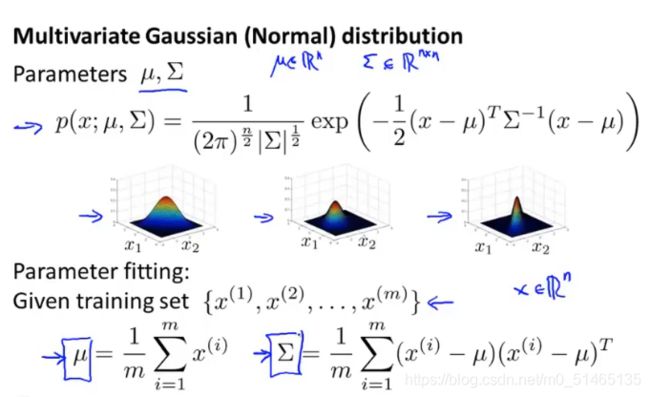综合起来，来开发一个异常检测算法：
1.首先用我们的数据集来拟合模型，通过设定μ和Σ来拟合p(x);2.接下来，如果当有新样本x（即一个测试样本）时，用多元高斯分布的公式来计算p(x),如果得到p(x)很小，就标记该样本为异常，如果p(x)大于参数ε，就不进行异常标记
多元高斯分布模型与原始模型有着怎样的关系呢？
原始高斯模型为p(x)=p(x1)p(x2)p(x3)…p(xn),原始模型相比多元高斯模型的轮廓（等高线）,原始模型总是轴对齐的，而多元高斯模型只有在Σ非对角线上都是0的时候，模型的等高线轮廓也是轴对齐的。所以原始高斯模型是多元高斯模型的一种特殊情况。
那么什么时候用原始模型，什么时候又该用多元高斯模型？
1.原始模型通常比多元高斯模型使用的多些，多元高斯模型在捕捉特征之间的关系方面有着很多优点。当用原始模型判断异常点时候，通常需要创建新特征x 来捕捉异常的组合值，而高斯模型能够自动捕捉不同特征之间的关系。
2.不过原始模型也有自己的优点，它的计算成本比较低，能够适应数量巨大的特征，而多元高斯模型计算成本非常大，即它能适应的特征数量少。
3.对于原始模型，即使有一个较小的有一定相关性的训练集，它也能顺利运行用来拟合模型p(x),而对于多元高斯分布，该算法有一些数学性质，就是必须保证样本的数量要大于特征的数量，如果在估计参数时不能满足该条件，那么这个Σ矩阵就是不可逆的（奇异矩阵），就无法使用多元高斯模型。

十一、推荐系统

15.1推荐系统的问题规划

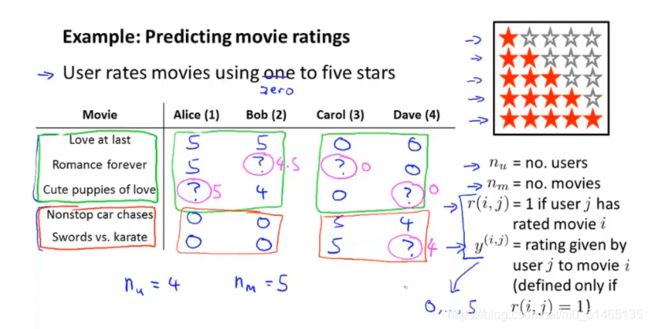
推荐系统的组成：接下来的例子中将观测电影评分的问题，假设让用户从零星到五星评价不同的电影，其中有五部电影和四个用户，下图为各用户所给评分，可以看出前两人喜爱爱情喜剧片，后两人喜欢看动作片，将nu表示用户数量，nm表示电影数量，r(i,j)=1代表用户j给电影i进行了评价，y(i,j)表示用户j对电影i所给出的评分，通过给出的r(i,j)和y(i,j)，去查找用户那些没有看的电影，并且试图预测这些电影的评价星级。

15.2基于内容的推荐算法

基于上个例子，如何才能预测这些未知量的值呢？
假设对于每一部电影，都有一个对应的特征集和两个特征x1和x2，其中x1衡量一部电影为爱情片的程度，x2来衡量一部电影为动作片的程度，那么每一部电影就可以用一个特征向量来表示，例如第一部电影有两个特征值x1=0.9和x2=0,再增加一个特征x0，因此x(1)向量就可以表示出来，x(2)x(3)依次类推。
为了做出预测，可以把每个用户的评价预测值，看作是一个线性回归问题，规定对于每一个用户j，要学习参数向量θj(一个n+1维向量），预测用户j评价电影i的值就是参数向量θ与特征量x(i)的内积
具体的系统推荐步骤：如果用户j评价了电影i，我们就将r(i,j)记为1，y(i,j)如果存在的话是对该电影的评价，其中xi是特定电影的一个特征向量，θj，它是每个用户xi的一个参数，对于每一个用户和电影通过内积的方式进行预测，用mj来表示评价电影j的用户数量，那么怎么学习θj？如下为计算θj的估计值的公式

使用梯度下降算法，最小化该函数来学习参数

15.3协同过滤

一种构建推荐系统的方法叫做协同过滤，协同过滤要观察大量的用户，观察这些用户的实际行为，来协同地得到更佳的每个人对电影的评分值，因为如果每用户都对一部分电影做出评价，那么每个用户都在帮助算法学习出更合适特征，这是协同过滤的意思，特征学习算法能够自行学习所要使用的特征。
假定每一部电影都有一些人来评价并告诉我们这部电影爱情的程度是多少又包含多少动作成分，但很难让每个人在看完每一部电影后告诉你这部电影包含多少爱情或动作，而且你通常还想要这两个特征之外的其他特征，那么该怎样得到这些特征呢？
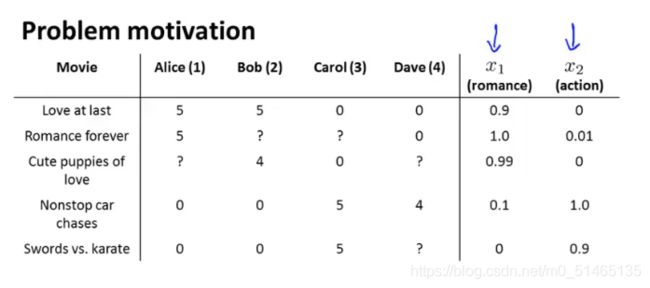首先假设有一个数据集，但不知道这些特征的值是多少，比如不知道一些用户对电影的评分，不知道每部电影的爱情、动作指数。但现在假设采访了每一位用户，而且每一位用户都告诉他们喜欢爱情或动作电影的程度，这样得到他们各自的θ，例如Alice非常喜欢爱情片，不喜欢动作片，可以得到如下θ1矩阵，依次类推。通过用户的喜好程度，这样可以推断得到大致的特征x1x2的值
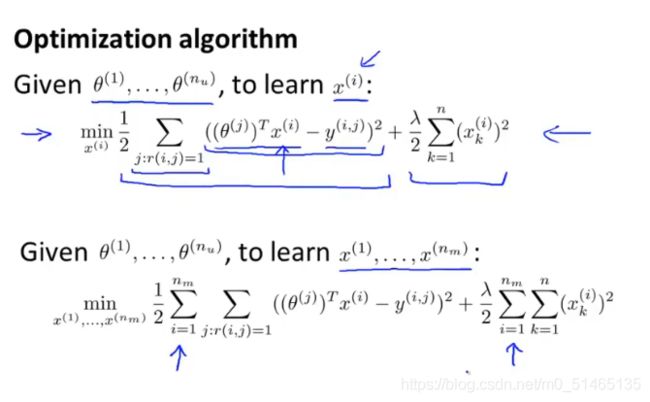
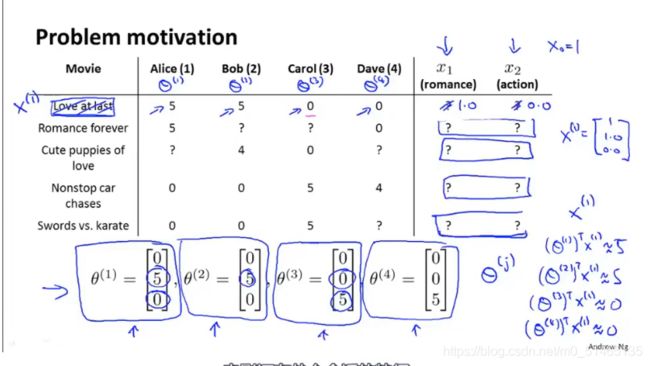接下来假设用户告诉了偏好，也就是用户提供了θ的值，而想要学习特征向量xi，首先提出下列优化问题，要做的就是选择特征xi

15.4协同过滤算法

假如你有了电影的特征xi，就可以解出如下最小化问题，找到用户参数θ。同样如果拥有参数θ，也可以用参数θ估计特征xi，办法就是通过解决如下最小化问题的到xi.不停的重复以上步骤计算x和θ。而现在介绍的算法可以将x和θ同时计算出来，方法就是将这两个优化目标函数结合为一个。
定义这个新的优化目标函数J,它是一个关于特征x和参数θ的代价函数
协同算法步骤：
1.首先把x和θ初始为小的随机值2.接下来用梯度下降或其他高级优化算法把这个代价函数最小化3.最后给出一个用户，该用户具有一些参数θ以及给出一部电影带有已知的特征x，可以预测该用户给出这部电影的评分

15.5低秩矩阵分解

如何推荐给定商品的与之相关的其他商品？
如下图，先得到所有用户对所有电影的评分，然后把他们分组写入矩阵
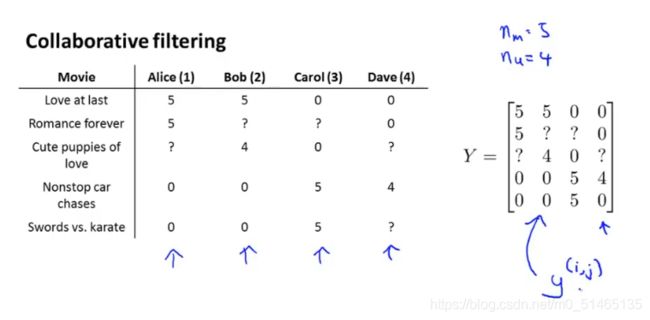低秩矩阵分解算法：Xθ^T
找到相关电影：对于每个商品（电影）i，学到若干个属性向量x^(i)，那么如何找到与之相关的电影呢？只需找到和该电影拥有最相似的特征的电影。

15.5均值归一化

从上节表格中加入第五个用户Eve，他没有给任何电影评分，那么如何推出他的评分呢？
μ取每一行的均值，再将Y减去均值重新得到Y，这样把每个电影评分都归一化，使得均分为零。接着对这个评分数据集使用协同过滤算法，用它来学习参数θ和特征xi.对于第五个用户Eve，可以得到其预测评分值向量为0+μ

十二、处理大数据集

16.1学习大数据集

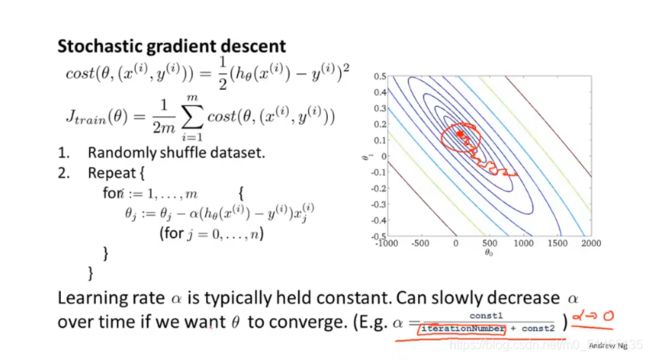
16.2随机梯度下降

梯度下降训练一个线性回归模型（逻辑回归、神经网络模型或者其他）
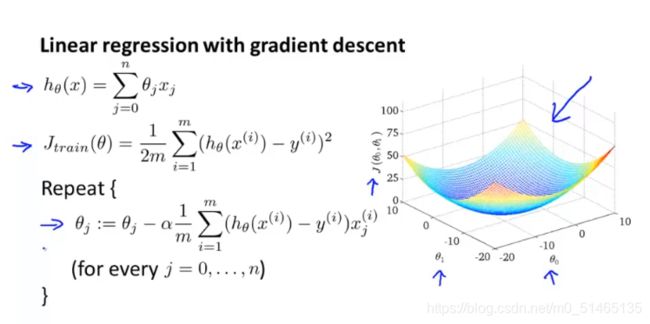但是当m相当大的时候，使用梯度下降时对m个样本进行求和，计算量就太大了。随机梯度下降不需要每次考虑全部的训练样本，仅需要将数据集打乱，且考虑一个训练样本，然后把参数稍微修改一下，使其对于该训练样本拟合得更好一些，完成后然后继续进行第二个训练样本，使得对于第二个训练样本拟合得更好一些，依次类推遍历整个数据集。（下图右边）

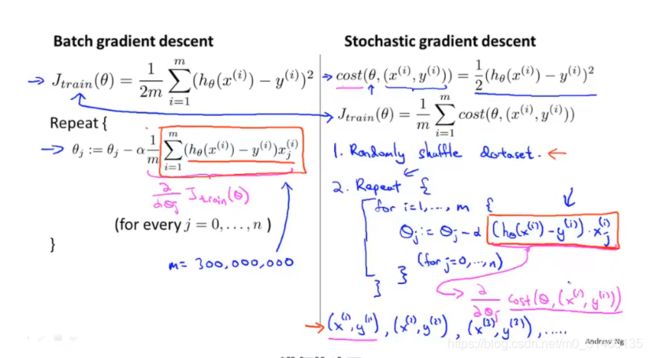
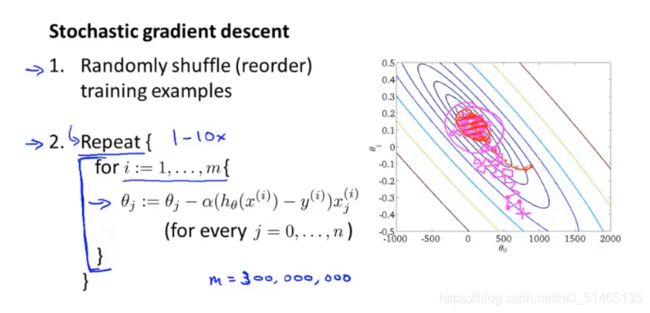
16.3Mini-Batch梯度下降

回顾：Batch梯度下降，每次迭代都要用到所有的m个样本；随机梯度下降每次迭代只需要使用一个样本；Mini-Batch梯度下降，介于二者之间，该算法每次迭代会使用b个样本，b是一个称为mini-batch大小的参数，通常b=10(2

16.4随机梯度下降收敛

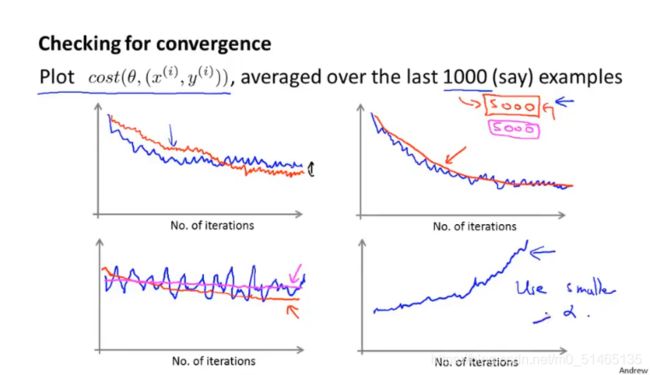
当使用随机梯度下降时如何确保调试过程已经完成，并且已经收敛到合适的位置呢，以及怎样调整随机梯度下降中学习速率α的值呢？
检查随机梯度下降算法收敛：每1000次迭代运算，求出前1000个cost函数的平均值，然后把它画出来，通过观察所画的图就能检查出随机梯度下降是否在收敛

十三、在线学习机制

17.1在线学习

例如：假设你提供运输服务，用户们来向你询问把包裹从A地运到B地的服务，假定你有一个网站，用户们登录网站来告诉你，他们想将包裹从哪里寄到哪里，然后你的网站开出运输包裹的服务价格，然后根据开出的服务价格，用户有时候会接收这个运输服务，则记为正样本，也有可能他们会走掉，此时记为负样本。我们假定想要一个学习算法来帮助优化我们想给用户开出的价格。假设我们获取了描述用户特点的特征（用户的数量、用户邮寄包裹的起始地及目的地、运送包裹的价格），用这些特征学习他们将会选择我们的服务来运输包裹的几率，以及给出他们会选择运输的价格。最后估计出在每种价格下用户选择使用我们服务的概率，因此可以估计出最合适的价格以达到最优化的选择服务次数和利润率。
假定一个连续运行的网站，以下就是在线学习算法所做的：获取与用户相关的特征xi，以及预测值y，利用得到的（x,y)数据来更新θ，以满足不断变化的用户群体

17.2Map-reduce（减少映射与数据并行）

比如我们想要拟合一个线性回归模型或者逻辑回归模型等等，首先从批量梯度下降开始，根据map-reduce的思想，我们把训练集分割成不同的子集，假定有四台电脑并行处理训练集数据，因此把数据分成4份，其中每一台机器用四分之一的训练集，这使得运算速度提高到原来的四倍，最后完成这些计算后，将这些temp变量重新整合在一起
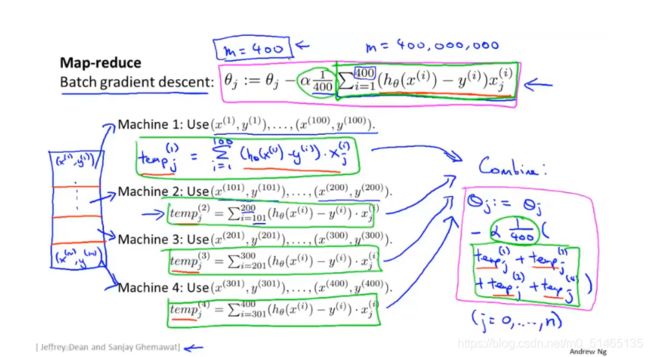Map-reduce技巧示意图
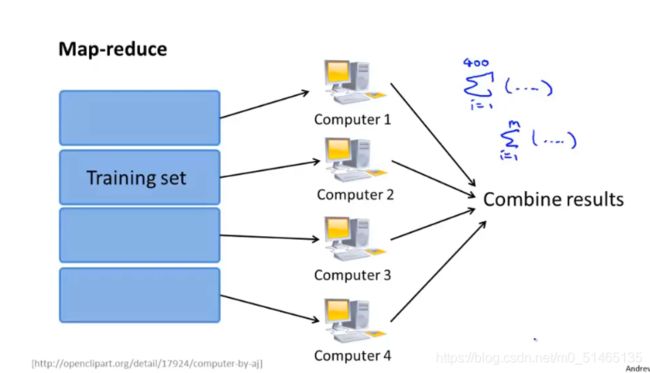如果想把Mapreduce应用在某种学习算法上通过多台电脑并行计算来实现加速，则需要考虑一个关键问题，你的学习算法是否可以表示成对训练集的一种求和，实际上很多学习算法都可以表示成对训练集的函数求和，而在大数据集上运行所消耗的计算量就在于需要对非常大的训练集进行求和，所以只要你的学习算法可以表示为对训练集的求和，那么就可以用Mapreduce将你的学习算法适用范围扩大到非常非常大的数据集
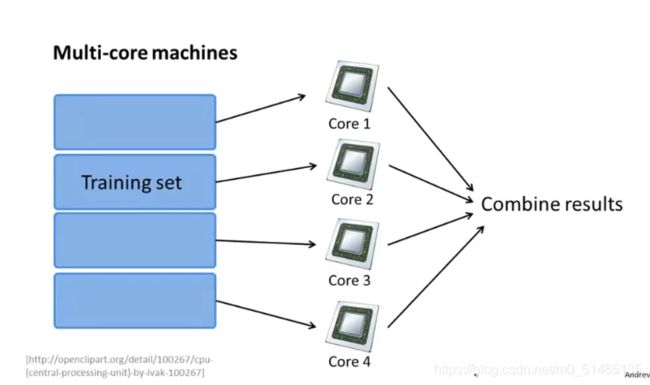
在单台电脑（四核）进行Maoreduce计算：

十四、OCR

18.1照片OCR技术与机器学习流水线

一个复杂的机器学习系统是如何组织起来的？机器学习流水线是怎样的？如何分配资源，来对下一步计划做出决定？
照片OCR全称为照片光学字符识别（Photo Optical Character Recognition),如何让计算机更好地理解这些照片的环境，读出图片中的文字信息，之后你如果想找到这个照片，只需要输入照片中的文字，计算机就能自动找出这张照片。
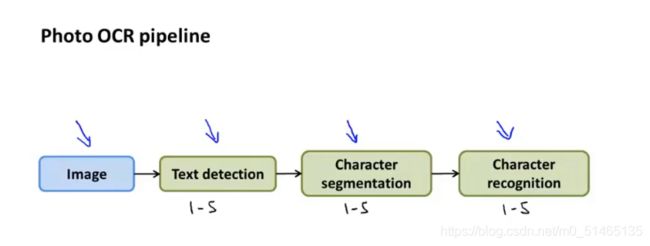
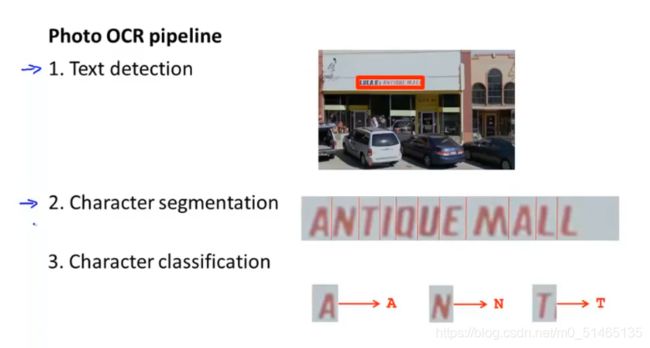
OCR机器学习流水线的几个步骤：1.将图像扫描一遍，找出照片中的文字信息，完成这一步后，将重点关注这些文字区域，并对区域中的文字进行识别，将这些文字显示并且记录下来。2.进行文字分离，将其分成一个个独立的字符区域3.分割好之后，用一个分类器，对这些可见的字符进行识别，这样就能识别出这句话。
照片OCR流水线

18.2滑动窗口分类器

建立一个行人检测系统：把比例的标准定为82*36，从数据集中收集一些正样本和负样本，然后可以将这些数据集在你的网络中训练或者使用其他学习算法，向其中输入一个82-36的图块，来对y进行分类，来划分每个图块是否包含行人，这就是一个应用监督学习的方法，来对图块进行处理。
现在假设得到一张新图作为一个测试集，尝试在图片中找到行人，首先在图片中选取一个矩形块，把这个矩形块传给分类器，来检测图块是否有行人，得到分类值y（1/0）后，接着将矩形块稍稍移动一点，再把这个矩形块传递给分类器，判断是否有人，依次类推。然而这样的矩形块只能识别某个特定大小的行人，因此将矩形块放大，以更大的矩形块，同样的放到分类器中，来检测行人。这就是如何训练一个监督学习，然后使用一个滑动窗口分类器，来找出图中的所有行人
矩形块每次移动的距离称为步长或者滑动参数，如果一次移动一个像素那么步长就为1，这样效果最好，但是计算成本较高，一般将步长设置为4像素或者更大像素，这就意味着矩形块每次移动的距离会多一些。
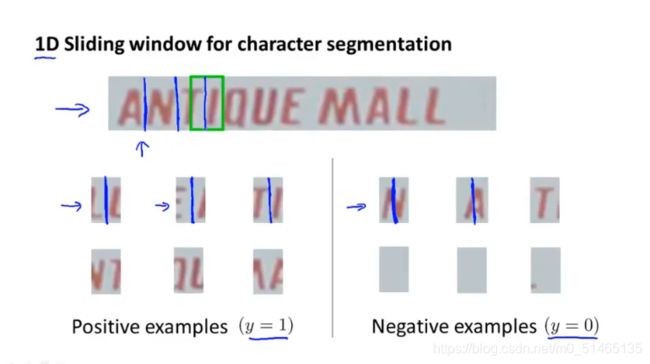
1维滑动窗口的特征分割

18.3获取大量数据和人工数据

从哪获取大量的训练数据集呢？人工数据合成可以得到大规模的训练集，第一种是自己创造数据，第二种已经有小的标签数据集，然后以某种方式扩充训练集，将较小的训练集转化为一个较大的训练集。
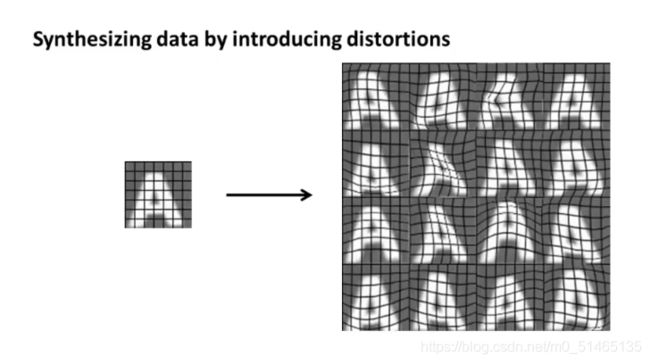
为了引入人工数据合成这个概念，用字符识别这个例子来讲解，假如我们收集到了一个大的标签数据集，要对正方形图像块进行识别，目标是输入一个图像块然后识别出图像块中央的字符，为了简化步骤将图像处理成灰度图像而不是彩色图像，例如用不同的字体生成字符，将其黏贴到任意不同的背景中，操作完成后现在就合成能以假乱真的数据，得到一个人造训练集。
另一个生成人工数据的方法是，使用现有的样本生成数据，进行人工拉伸（人工扭曲），这样就可以将一个数据集变成16个新的样本，采用这种办法你就能将一个小的标签训练集扩充为一个更大的训练集。
语音识别的例子，假定你有一些音频片段，从语音片段中识别出现的单词，假定有一个原始带标签的训练样本，那么如何扩充数据集呢，那就是引入额外的语音失真到数据集中，例如加入背景音来模拟手机通话信号不好的情况。
当引入失真合成数据时，如果试图让自己合成的数据合理。
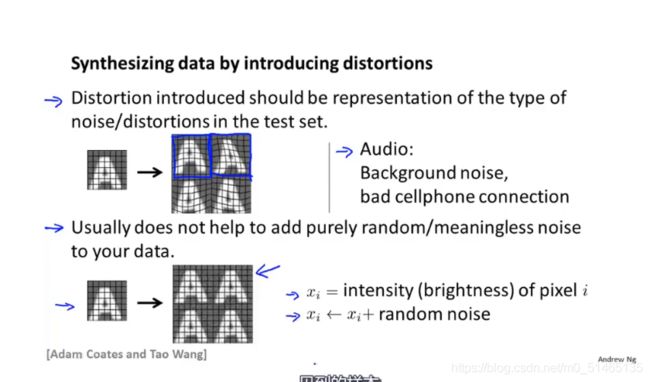1.在花大力气想办法生成人工训练样本之前通常最好先确保你的分类器偏差较低，这样更多的训练数据才会真正起作用，标准的做法是绘制一个学习曲线来确保有一个低偏差高方差的分类器，如果分类器偏差太高那么可以尝试持续增加分类器的特征数量或者增加神经网络隐藏单元的数量，直到偏差值降低，然后再花精力到生成大量的人工训练集上
2.获得当前数据集数量的10倍，需要花费多大努力？1.人工合成数据集2.自己收集数据或者添加标签3.使用“众包”

18.4上限分析

在设计机器学习项目的时候，通常会制定一条流水线（数据预处理、特征提取、…之类），根据流水线完成项目。

在完成项目的时候，通常对其精确率进行优化，可采取上限分析（Ceiling analysis），分析最有可能提高精确率的地方。

流水线：
如下图所示为OCR（光学字符识别）的流水线：

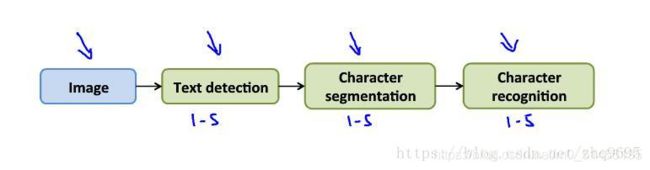
上限分析作用是在于发现流水线中哪个步骤优化以后，会给整个模型带来最大的优化

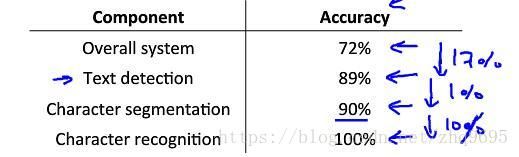
在上述例子中，整体的精确率为 72% ，如果人为进行文本识别（将文本识别的精确率提高至 100% ），则整体精确率为 89% ，提高了 17% ，如果继续人为进行字符分割（将字符分割的精确率提高至 100% ），则整体精确率为 90% ，提高了 1% ，如果继续人为进行字符识别（将字符识别的精确率提高至 100% ），则整体精确率为 100% ，提高了 10% 。由此可见，优化文本识别，会给整个模型带来最大的优化。

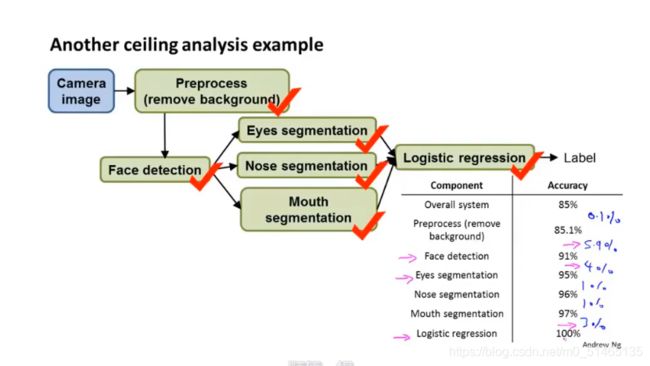
上限分析的实例：假如设计了如下工作流：图像预处理（将背景去除）→人脸检测（通常运用滑动窗口分类器）→眼睛检测、鼻子检测、嘴巴检测→输入给某个逻辑回归分类器→分类器给出标签y
假如整个系统的准确率为85%，首先还是找到测试集，人工地标记出哪些是背景，然后手动把背景删掉，然后观察准确率提高多少，发现提升并不大，所以不需要花费大量的时间进行背景移除上。接下来再遍历测试集，给出正确的脸部识别图案，依次进行眼睛鼻子嘴巴的分割，发现提升较大 。

完结