(学习笔记)人工神经网络——感知器
概述
感知器模型由心理学家Rosenblatt于1958年提出,并发表在论文“The Perceptron: A Probabilistic model for information storage and organization in the brain"中。1962年他又出版了著作《principles of neurodynamics: perceptrons and thr theory of brain mechanisms》,本书详细地阐述了感知器的基本理论及假设背景,并介绍了如感知器收敛定理等一些重要的概念及定理证明。
作为人工神经网络中的一种典型结构,感知器的神经元采用的是MP模型,在研究中还发现单层感知器只能在线性可分情况下进行模型分类,而且只能解决数据本身是线性可分的二分类问题。
1961年minsky指出了单层神经网络不能解决异或问题,也就证明感知器的运算能力有限。后来他与papert一同出版了《perceptrons: an introduction to computational geometry》,对单层感知器的局限性作了严格的数学证明和分析。
指导1987年,书中的错误才得到了校正,并更名《perceptrons: expanded edition》。
感知器
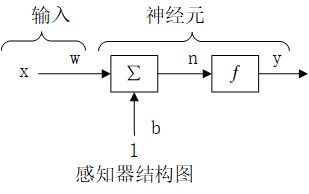
结构:感知器即单层神经网络,也即神经元,是组成神经网络的最小单元。
其中,w和b为感知器模型参数,w表示全权值,b表示偏置,wx表示w和x的内积。
在感知层进行学习时,每一个样本都将作为一个刺激输入神经元。输入信号是每一个样本的特征,期望的输出是该样本的类别。当输出与类别不同时,可以通过调整突触权值和偏置值,直到每个样本的输出与类别相同。
原理:输入向量X=(x1,x2,xr)T为样本的特征维,对应权值向量W=(w1,w2,wr)为一组参数。因此线性方程WX+b=0对应于空间中的一条直线。Wi是该直线法向分量,也是权值矩阵的某一行向量;b为直线的截距。该直线确定的判定边界将空间内的不同元素划分为正负两类,通过学习得到感知器模型,对于新的新输入向量可预测其输出类别。
学习策略:选取使损失函数值最小的模型参数w和b。损失函数及所有误分类点到超平面的距离之和即为: L = − 1 ∥ w ∥ y i ( w ∙ x i + b ) L=-\frac{1}{\parallel w\parallel}y_i(w\bullet x_i+b) L=−∥w∥1yi(w∙xi+b) ,其中,C为误分类点组成的训练集,||w||为w的二范数,不影响感知学习算法的最终结果,因此在不考虑的情况下损失函数为: L ( w , b ) = − ∑ x i ∈ C y i ( w ∙ x i + b ) L(w,b)=-\sum_{{x}_{i\in C}}{y_i(w\bullet x_i+b)} L(w,b)=−∑xi∈Cyi(w∙xi+b)。
对于给点训练集C,损失函数L(w,b)是w和b的连续可导的非负函数。如果没有误分类点则损失函数的值为零,且当误分类点越少时,误分类点到超平面的总距离就越少,即损失函数的值就越小。
单层感知器
模型: 单层感知器是最简单的一种人工神经网络结构,包含输入层和输出层。输入层只负责接受外部信息,每个输入节点接收一个输入信号。输出层也称为处理层,具有信息处理能力以及向外部输出处理信息。
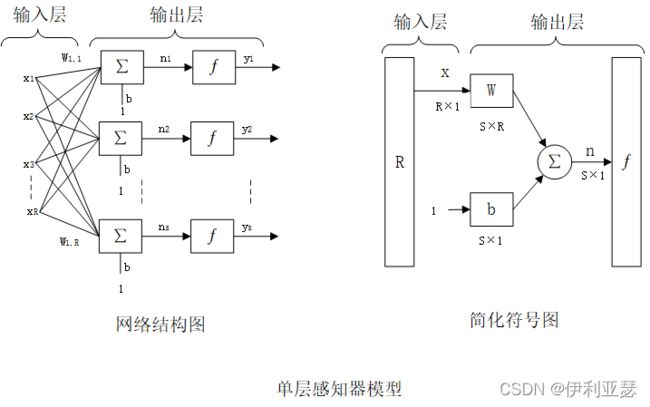
网络中有S个感知器神经元,R个输入元素,W为S*R权值矩阵。输出层第i个神经元的输出为 y i = f ( n i ) = f ( ∑ j = 1 R w i , j x j + b ) y_i=f(n_i)=f(\sum_{j=1}^{R}{w_{i,j}x_j+b}) yi=f(ni)=f(∑j=1Rwi,jxj+b) 。
功能:
1.两输入情况:
输入向量x=(x1,x2)T,该向量在空间上形成一个二维的平面,用该平面来表示输入的样本数据,则输出为
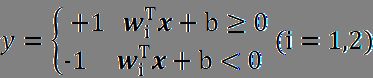
直线方程 w i T x + b = 0 {w}_i^T{x}+b=0 wiTx+b=0 将二维平面内的样本数据分为两部分,处在直线上方的数据输出结果为+1,下方的为-1。
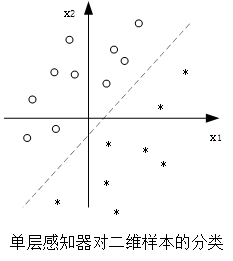
直线的斜率和截距决定了直线在二维平面内的位置,即感知器的全职和偏置值确定了分界线在样本空间的位置。通过调节感知器的权值和偏置值,总是可以找到一条分界线将二维空间内的样本分为两类。
2.三输入情况:
此时 w i T x + b = 0 {w}_i^T{x}+b=0 wiTx+b=0 在三维空间内形成一个分界面,钙粉界面将三维空间内的样本数据分为两类,分界面左下方的输出结果为+1,右上方的输出为-1。同理,通过改变感知器的权值和偏置值的大小可以找到一个平面将三维空间内的样本数据分类。
3.n输入情况:
n个输入向量在几何上构成了一个n维空间,方程 w i T x + b = 0 {w}_i^T{x}+b=0 wiTx+b=0 在空间内形成了一个超平面,通过改变感知器的权值和偏置值的大小,从而改变该超平面的位置,最终可将输入的样本数据分为两类。
总之,单层感知器具有分类功能,其思想就是通过改变感知器的权值和偏置值的大小,改变分界线或分界面的位置,将输入样本分为两类。
学习算法:
基本思想是逐步地将样本输入到网络中,根据输出的结果和理想输出之间的差值来调整网络中的权值矩阵,也就是求解损失函数L(w,b)的最优化问题。采用随机梯度下降法,然后用梯度下降法不断地逼近目标函数的极小值。
极小化目标函数为: m i n L ( W , b ) = − ∑ x i ∈ C y i ( W ∙ x i + b ) minL({W},b)=-\sum_{{x}_{i\in C}}{y_i({W}\bullet{x}_i+b)} minL(W,b)=−∑xi∈Cyi(W∙xi+b) ,C为误分类集合。极小化过程不是一次使C中所有误分类点的梯度下降,而是通过迭代实现。其规则为 h ( t + 1 ) = h ( t ) − η ∇ ( h ) h(t+1)=h(t)-\eta\nabla(h) h(t+1)=h(t)−η∇(h) , η ( 0 < η < 1 ) \eta(0<\eta<1) η(0<η<1) 为步长,也称其为学习率,t为迭代次数, ∇ ( h ) \nabla(h) ∇(h) 是梯度, h ( t + 1 ) h(t+1) h(t+1)是更新后的值。
假设误分类点集合C是固定的,则损失函数L(W,b)的梯度为: ∂ L ( W , b ) ∂ W = − ∑ x i ∈ C y i x i \frac{ \partial L( {W},b)}{\partial{W}}=-\sum_{{x}_i\in C}{y_i{x}_i} ∂W∂L(W,b)=−∑xi∈Cyixi , ∂ L ( W , b ) ∂ b = − ∑ x i ∈ C y i \frac{\partial L(W,b)}{\partial b}=-\sum_{ {x}_i\in\ C}y_i ∂b∂L(W,b)=−∑xi∈ Cyi
按梯度下降法得到新的W和b,对其进行更新,即 W ( t + 1 ) = W ( t ) + η y i x i W(t+1)=W(t)+\eta y_i{x}_{i} W(t+1)=W(t)+ηyixi, b ( t + 1 ) = b ( t ) + η y i b(t+1)=b(t)+\eta y_i b(t+1)=b(t)+ηyi 。通过不断迭代更新W和b的值,使损失函数不断减小,直至为0。此时,训练集中没有误分类点,分类过程结束。
直观解释: 当误分类集合中有一元素被误分类,即该元素位于分离超平面的错误一侧是,即调整感知器的权值W和偏置b的值,使分离超平面向该误差分类点的一侧移动,以减少该误差分类点与超平面的距离,直至超平面越过该误差分类点使其被正确分类。
局限性:
单层感知器的分类判决方程是线性方程,所以单层感知器是无法解决线性不可分的问题,只能解决线性可分问题。因此,在单层的基础上提出了多层感知器理论。
案例展示:
给定输入向量P=[-0.6 -0.4 0.4;0.6 0 0.3;0.6 -0.3 0.2]和目标向量T=[1 1 0],设计一个单层感知器对输入向量组Q=[0.5 0.7 -0.4; -0.6 -0.7 0.5; 0.6 0.1 -0.3]进行分类。
%%创建,训练,存储神经网络
clear all %清除所有原内存变量
clc %清屏
P=[-0.6 -0.4 0.4;0.6 0 0.3;0.6 -0.3 0.2] %输入训练向量
T=[1 1 0] %目标向量
pr=[-1 1;-1 1;-1 1;] %设置感知器网络输入向量每个元素的值域,也即每个坐标轴的值域
net=newp(pr,1) %建立感知器网络
handle=plotpc(net.iw{1},net.b{1}) %返回划线的空点,绘制分类线时将旧线删除
net.trainParam.epochs=50 %设置训练次数最大为50次
net=train(net,P,T) %训练感知器网络
save net41 net %储存训练后的网络
%%网络仿真
load net41 net %加载训练后的网络
Q=[0.5 0.7 -0.4; -0.6 -0.7 0.5; 0.6 0.1 -0.3] %测试样本
Y=sim(net,Q) %仿真结果
iw1=net.iw{1} %输出训练后的权值
b1=net.b{1} %输出训练后的偏置值
plotpv(Q,Y) %绘制分类结果
plotpc(iw1,b1) %绘制分类线
title('样本分类')
多层感知器
结构:
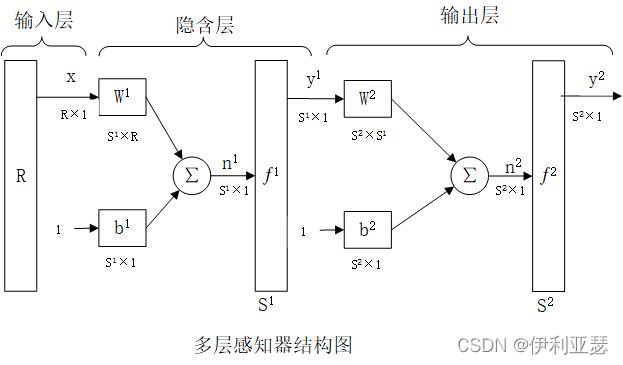
多层感知器包含隐含层和输出层,这两个网络是全连接的,即在任意层上的一个神经元可以与他之前的层上的所有节点或神经元连接起来。隐含层单元是“隐含”于神经网络输入层和输出层之间的感知器层其信息来源于输入层,其输出作为下一隐含层的输入,以此类推,一直传递到输出层。
1.每个神经元都包含一个可微的非线性传递函数。
2.在输入层和输出层之间有一个或多个隐含神经元,这些神经元不断地从输入向量中提取有用的特征值,使网络可以完成更加复杂的任务。
3.网络表现出高度的连续性,其强度是由网络的权值决定的。可以通过改变突触连接数量和权值改变网络的连续性。
功能:
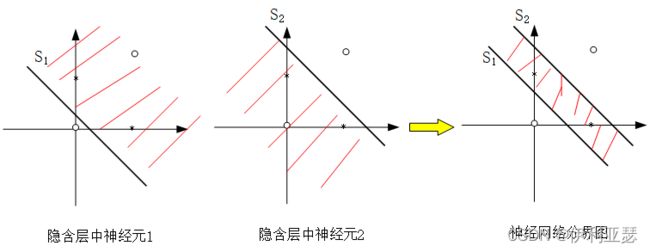
1.模式分类
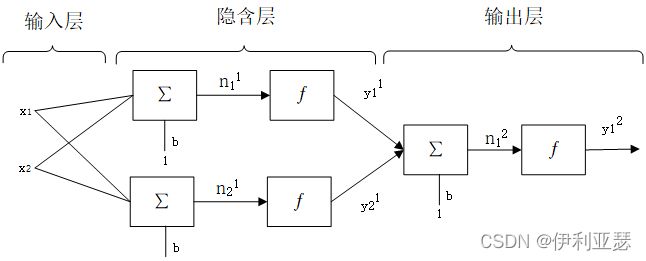
以隐含层两个神经元为例,两个神经元分别产生两个边界S1和S2。输出层执行一个AND操作,将两边界结合起来。如图所示
构建一个如图的网络结构来说明多层感知器的逼近功能,该网络中的传递函数选用对数S型函数,输出层中的传递函数选用线性函数。
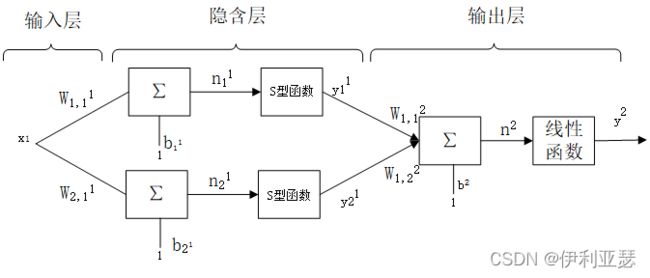
则隐含层的输出为 y 1 = f 1 ( n 1 ) = 1 1 + e − n 1 y^1=f^1(n^1)=\frac{1}{1+e^{-n^1}} y1=f1(n1)=1+e−n11 ,输出层的输出为 y 2 = f 2 ( n 2 ) = n 2 y^2=f^2(n^2)=n^2 y2=f2(n2)=n2 。在一定的权值与偏置值之下输出如下响应
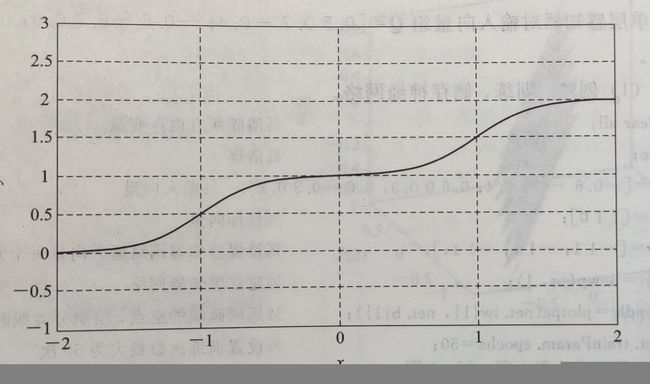
在神经网络响应的过程中,通过调整网络的权值和偏置值,可以使图中的曲线陡度和位置发生改变,直到达到期望的曲线。在网络结构中,隐含层选用对数S型传递函数,输出层选用线性传递函数,就几乎可以在任意精度逼近期望函数。
学习算法:
在训练多层感知器学习的时候,通常使用在监督学习方式下的误差反向传播算法。误差反向传播学习过程由信号的正向传播与误差的反向传播两个过程组成。
1.正向传播:输入向量作用于网络的感知节点上,经过神经网络一层接一层的传播,最后产生的一个输出作为网络的实际响应。在前向通过时,神经网络的突触权值保持不变。
2.反向传播:突触权值全部根据误差修正规则来调整,误差信号由目标响应减去网络的实际响应而产生。通过调整突出的权值使网络的实际相应接近目标响应。
随着信号的正向传播过程与误差的反向传播过程的交替反复进行,网络的实际输出逐渐向各自所对应的期望输出逼近,网络对输入模式响应的正确率也不断上升。
案例展示:
异或问题:
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
%%创建,训练,存储神经网络
clear all %清除所有原内存变量
clc %清屏
pr1=[0 1;0 1] %设置随机感知器层输入向量每个元素的值域
net=newp(pr1,3) %设置随机感知器层的值域和神经元数
net1.inputweights{1}.initFcn='rands' %指定随机感知器层权值初始化函数为随机函数
net1.biases{1}.initFcn='rands' %指定随机感知器层偏置值初始化函数为随机函数
net1=init(net1) %初始化随机感知器层
iw1=net1.iw{1} %给随机感知器层的权值向量赋值
b1=net1.b{1} %给随机感知器层的偏置值赋值
%%随机感知器层仿真
x1=[0 0;0 1;1 0;1 1] %随机感知器层的输入向量
[y1,pf]=sim(net,x1) %随机感知器层仿真
%%初始化第二感知器层
pr2=[0 1;0 1;0 1] %设置输出层输入向量每个元素的值域
net2=newp(pr2,1) %s设置输出层的值域和神经元数
net2.trainParam.epochs=10 %设置最大训练次数为10次
net2.trainParam.show=1 %每间隔一步显示一次训练结果
x2=ones(3,4) %初始化输出层的输入向量
x2=x2.*y1 %随机感知器的输出结果作为输出层的输入向量
t2=[0 1 1 0] %输出层的目标向量
[net2,tr2]=train(net2,x2,t2) %训练输出层
epoch2=tr2.epoch %输出训练过程经过的每一步长
perf2=tr2.perf %输出层每一步长训练结果的误差
iw2=net2.iw{1} %输出层的权值向量
b2=net2.b{1} % 输出层的偏置值
save net42 net1 net2 %存储训练后的网络
%%网络仿真
load net42 net1 net2 %加载训练后的网络
x1=[0 0;0 1;1 0;1 1] %随机感知器层输入向量
y1=sim(net1,x1) %随机感知器层仿真结果
y2=ones(3,4) %初始化输出层的输出向量
x2=x2.*y1 %随机感知器层输出结果作为输出层的输入向量
y2=sim(net2,x2) %输出层仿真结果