第27期 Datawhale 组队学习 吃瓜教程——西瓜书+南瓜书第六章 / 周志华《机器学习》
前言
支持向量机(SVM)个人理解是建立在线性空间的基础之上,提供一种算法,使得分开的曲线距离正负样本距离较远,以增加其泛化性能。
目录
- 前言
- 1. 支持向量机
-
- 1.0 须知知识点
-
- 1.0.1 超平面
-
- 1.0.1.1 基础知识
- 1.0.1.2 数学推导
- 1.0.1.3 可参考文献:
- 1.0.2 几何间隔
-
- 1.0.2.1 基础知识
- 1.0.2.2 可参考文献
- 1.0.3 sign函数
-
- 1.0.3.1 定义
- 1.0.3.2 可参考文献
- 1.1 算法原理
- 1.2 对偶原理及KTT
-
- 1.3 软间隔与支持向量回归
-
- 1.3.1软间隔
-
- 1.3.1.1软间隔与硬间隔的区别
- 1.3.1.2 核函数
- 1.3.2 支持向量机
- 参考文献
1. 支持向量机
1.0 须知知识点
1.0.1 超平面
1.0.1.1 基础知识
1.0.1.2 数学推导
1.0.1.3 可参考文献:
- 超平面详解
- SVM超平面的理解
1.0.2 几何间隔
1.0.2.1 基础知识
1.0.2.2 可参考文献
- 斯坦福《机器学习》Lesson6感想———1、函数间隔和几何间隔
1.0.3 sign函数
1.0.3.1 定义
1.0.3.2 可参考文献
什么是sign函数(符号函数)
1.1 算法原理
定义:从几何角度,对线性可分数据集,支持向量机就是找距离正负样本都最远的超平面,相比于感知机,其解是唯一的,且不偏不倚,泛化性能更好。


1.2 对偶原理及KTT
遇到等式和不等式约束优化问题怎么办:
1.引入拉格朗日函数和KKT条件,转为无约束优化问题
求导不好解怎么办:
2.转为求对偶问题,更换求导代入再求导的顺序(即先极小再极大)
注意:求解时需要满足KKT条件
普通同学的解法:消元求导
聪明同学的解法:建立梯度关系,求导,解多元方程
天才同学的解法:转为对偶问题,消元求导
在SVM的应用
SVM不就是在一大堆不等式的约束的最优化问题吗,所以当然用天才同学的解法,转为对偶问题,消元求导,可以带来以下好处:
1.方便求解
2.自然的引入核函数
在最大熵模型的应用
最大熵原理认为,学习概率模型时,在所有可能的概率模型中,熵最大的模型是最好的模型,简单说就是,在没有更多信息下,那些不确定的部分是“等可能的”。
也就是约束等式下,熵最大问题,可等价转为拉格朗日对偶问题。
从放弃到再入门之拉格朗日对偶问题推导
1.3 软间隔与支持向量回归
1.3.1软间隔
1.3.1.1软间隔与硬间隔的区别
硬间隔:所有的样本都满足约束条件
软间隔:允许一定量的样本不满足约束条件
1.3.1.2 核函数
如果在一个二维平面上有[(0,0),(0,1),(1,0),(1,1)],其中[(0,0),(1,1)]属于一类,[(0,1),(1,0)]属于另
外一类,那么我们用支持向量机就不能进行划分。所以在此我们引入核函数。
核函数的定义:支持向量机通过某非线性变换 φ( x) ,将输入空间映射到高维特征空间。特征空间的维数可能非常高。如果支持向量机的求解只用到内积运算,而在低维输入空间又存在某个函数 K(x, x′) ,它恰好等于在高维空间中这个内积,即K( x, x′) =<φ( x) ⋅φ( x′) > 。那么支持向量机就不用计算复杂的非线性变换,而由这个函数 K(x, x′) 直接得到非线性变换的内积,使大大简化了计算。这样的函数 K(x, x′) 称为核函数。
数学上可以证明,如果原始空间是有限维,即属性数有限,则一定存在一个高维特征空间使样本可分。将样本从原始空间映射到一个更高维的特征空间 , 使样本在这个特征空间内线性可分。
二维变三维
核函数在这里的作用是将样本数据扩展到高维。
每一个核函数都隐式的定义了一个特征映射函数。
1.3.2 支持向量机
不管直接在原特征空间,还是在映射的高维空间,我们都假设样本是线性可分的。虽然理论上我们总能找到一个高维映射使数据线性可分,但在实际任务中,寻找一个合适的核函数核很困难。此外,由于数据通常有噪声存在,一味追求数据线性可分可能会使模型陷入过拟合,因此,我们放宽对样本的要求,允许少量样本分类错误。这样的想法就意味着对目标函数的改变,之前推导的目标函数里不允许任何错误,并且让间隔最大,现在给之前的目标函数加上一个误差,就相当于允许原先的目标出错,引入松弛变量 ξ i ≥ 0 \xi_i\geq0 ξi≥0 ,公式变为:
那么这个松弛变量怎么计算呢,最开始试图用0,1损失去计算,但0,1损失函数并不连续,求最值时求导的时候不好求,所以引入合页损失(hinge loss):
但这个代价需要一个控制的因子,引入C>0,惩罚参数,即:
可以想象,C越大说明把错误放的越大,说明对错误的容忍度就小,反之亦然。当C无穷大时,就变成一点错误都不能容忍,即变成硬间隔。实际应用时我们要合理选取C,C越小越容易欠拟合,C越大越容易过拟合。
所以软间隔的目标函数为:
其中:
参考文献
- 什么是sign函数(符号函数)
- 从放弃到再入门之拉格朗日对偶问题推导





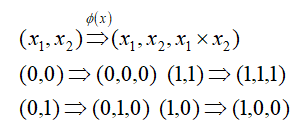
![[公式]](http://img.e-com-net.com/image/info8/5d6835927eff48ef9dad2e295e3dad35.png)
![[公式]](http://img.e-com-net.com/image/info8/a0602ce0889b4de0924d9b792a24d114.jpg)

![[公式]](http://img.e-com-net.com/image/info8/b3e4c2aee77341bf86d4a99982863da8.png)
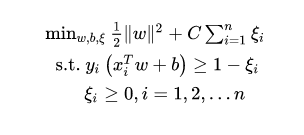
![[公式]](http://img.e-com-net.com/image/info8/1256b649f3a64aafacbf8116b07819c2.png)