tensorflow学习（一）基础数学

前言：
上章讲述了环境搭建，这章主要讲述需要的数字基础
矩阵，编导数 ,最小二乘法,梯度,学习率,交叉熵等

1:矩阵
1> 矩阵的加减法
这个好理解 ，对应位置一一加减

2>矩阵的乘法

A矩阵= MP (M行P列) B矩阵= PN (P行N列) C=AB = MN (M行N列）
计算规则: A的第一行 分别 乘 B的第一列 做位结果的第一行第一列 （C11 = SUM(A1? * B?1) ）


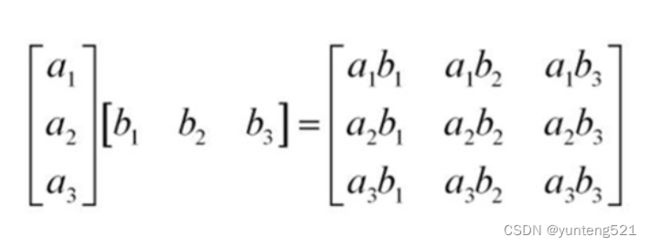
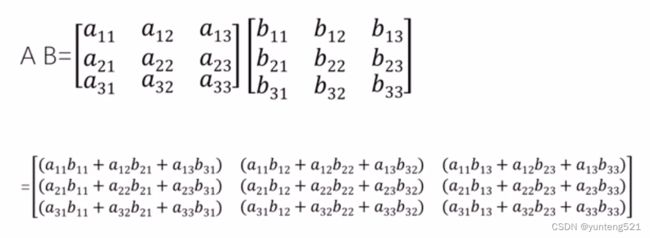
2>矩阵求逆（矩阵的除法）
A/B = A*(1/B)= A*(B的逆矩阵)
先求B得可逆矩阵 再 A* B的可逆矩阵
设A是数域上的一个n阶矩阵，若在相同数域上存在另一个n阶矩阵B，使得： AB=BA=E (E为单位矩阵)，则我们称B是A的逆矩阵，而A则被称为可逆矩阵
参考：https://www.bilibili.com/read/cv2920478
单位矩阵:

第一种 待定系数法

第二种 初等变换法

第三种 伴随阵法

2:最小二乘法
参考：https://blog.csdn.net/ccnt_2012/article/details/81127117


3:梯度和学习率
参考：https://blog.csdn.net/ISMedal/article/details/87893200

上文已经提及，梯度就是对损失函数求导的导数值，它表示“如果稍稍改变权重参数的值，损失函数的值会如何变化”。我们想要损失函数往最小的方向走，那么梯度的方向就是各点处函数值减小最多的方向。注意，梯度的方向并不一定指向最小值，但在每一点处，沿着梯度可以最大限度地减小损失函数的值。
像这样，通过不断沿着梯度方向前进，逐渐减小函数值的过程，就是梯度法。梯度法是解决机器学习最优化问题的常见方法。我们通过公式来描述梯度法，参数的迭代过程可以描述为
​
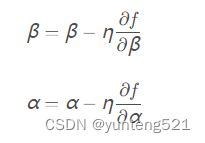
其中，η 表示每次迭代的更新量，被称为学习率。它决定在一次学习中应该学习多少，以及在多大程度上更新参数。学习率是一个超参数（不能通过数据训练得到，而需要人工设定的参数），一般这个值过大或过小都无法抵达一个“好的位置”。

学习率 设置 参考:https://zhuanlan.zhihu.com/p/390261440
初始学习率的范围一般在1e-6(0.000001)到1之间。可以根据经验或直觉，拍脑袋设定一个初始学习率。不过，还有更科学的方法来寻找初始学习率。
大致思想是，观察损失或准确率随学习率变化的曲线，然后根据一定策略选择最好的学习率作为初始学习率。

4:交叉熵
参考：https://zhuanlan.zhihu.com/p/530496055
1>对数换底公式
参考：https://blog.csdn.net/Gou_Hailong/article/details/122829929

2>熵
参考:https://zhuanlan.zhihu.com/p/465760651
https://www.itdaan.com/blog/2018/01/25/604818a492c15cd6bcb7a6790ca0ace7.html

对于某个事件，有 n 种可能性，每一种可能性都有一个概率 p(xi); p ( x i )
这样就可以计算出某一种可能性的信息量。举一个例子，
假设你拿出了你的电脑，按下开关，会有三种可能性，
下表列出了每一种可能的概率及其对应的信息量
序号 事件 概率p 信息量I
A 电脑正常开机 0.7 -log(p(A))=0.36
B 电脑无法开机 0.2 -log(p(B))=1.61
C 电脑爆炸了 0.1 -log(p©)=2.30
注：文中的对数均为自然对数 e 2.78…
公式如上面 1 所示
电脑开机问题计算如下
H ( X ) = − [ p ( A ) l o g ( p ( A ) ) + p ( B ) l o g ( p ( B ) ) + p ( C ) ) l o g ( p ( C ) ) ] = 0.7 × 0.36 + 0.2 × 1.61 + 0.1 × 2.30 = 0.804

然而有一类比较特殊的问题，比如投掷硬币只有两种可能，字朝上或花朝上。买彩票只有两种可能，中奖或不中奖。我们称之为0-1分布问题（也叫二项分布），对于这类问题，熵的计算方法可以简化为如下算式：

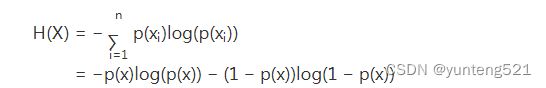
3>相对熵（KL 散度）
相对熵（Relative Entropy），也叫 KL 散度 (Kullback-Leibler Divergence)，具有非负的特性。用于衡量两个分布之间距离的指标，用 分布近似 的分布，相对熵可以计算这个中间的损失，但是不对称（ 对 和 对 不相等），因此不能表示两个分布之间的距离，这种非对称性意味着选择 还是 影响很大。当 时， 相对熵（ 散度）取得最小值 。
相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异
即如果用P来描述目标问题，而不是用Q来描述目标问题，得到的信息增量。

在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]
直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

KL散度的计算公式：

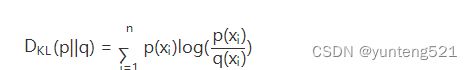
n为事件的所有可能性。
DKL D K L 的值越小，表示q分布和p分布越接近

4>交叉熵

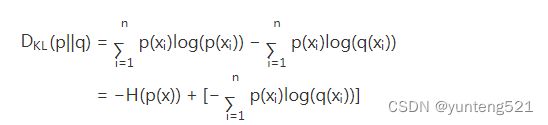
等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：
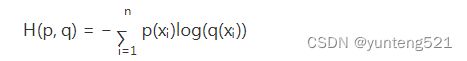在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即 DKL(y||ŷ ) D K L ( y | | y ^ ) ，由于KL散度中的前一部分 −H(y) − H ( y ) 不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。