情感分类与朴素贝叶斯
本文介绍一种机器学习分类算法——朴素贝叶斯算法及其在NLP中的应用。具体实现部分可参考朴素贝叶斯用于情感分类的实现
NLP中的分类
许多自然语言处理任务涉及分类,分类也是人类和机器智能的核心。
- 文本分类
文本分类是将整个文本或文档赋值标签或类别的任务。文本分类的应用包括,主题分类(subject category classification)、情感分析(sentiment analysis)、垃圾邮件检测(spam detection)等。 - 其他分类任务
分类对于文档级别以下的任务也很重要。比如句号消歧(period disambigution)用来判断句号是否代表句子结束还是单词的一部分、分词(word tokenization)用来判断某个字母是否为单词的边界、词性标注(part-of-speech tgger)等。 - 分类方法
对文本进行分类的一种方法是使用手写规则。在语言处理的许多领域中,基于规则的分类器构成了最先进的系统,或者至少是系统的一部分。然而规则可能会很脆弱,而且对于某些任务,人类不一定擅长制定规则。语言处理中的大多数分类都是通过监督机器学习来完成的。有许多机器学习算法用来构造分类器,可以分为生成分类器如朴素贝叶斯和判别分类器如逻辑回归。生成分类器是从输入中学习特征,返回最有可能产生这种输入的类别,而判别分类器是对不同类别进行区分。尽管判别方法通常更准确也更常用,但生成分类器仍占有一席之地,值得进行探讨。
朴素贝叶斯算法
朴素贝叶斯是概率分类器,也就是给定文档 d d d,所有类别 c ∈ C c \in C c∈C,分类器产生有最大后验概率的类别 c ^ \hat{c} c^。 c ^ = a r g m a x c ∈ C P ( c ∣ d ) (1.1) \hat{c} = argmax_{c \in C}P(c|d) \tag{1.1} c^=argmaxc∈CP(c∣d)(1.1)
根据贝叶斯推导,上式可转化为: c ^ = a r g m a x c ∈ C P ( c ∣ d ) = a r g m a x c ∈ C P ( d ∣ c ) P ( c ) P ( d ) (1.2) \hat{c} = argmax_{c \in C}P(c|d)=argmax_{c \in C}\frac{P(d|c)P(c)}{P(d)} \tag{1.2} c^=argmaxc∈CP(c∣d)=argmaxc∈CP(d)P(d∣c)P(c)(1.2)
我们可以将等式(1.2)进行简化,丢掉分母 P ( d ) P(d) P(d)。因为每次计算时 P ( d ) P(d) P(d)是不变的。 c ^ = a r g m a x c ∈ C P ( d ∣ c ) ⏞ l i k e l i h o o d P ( c ) ⏞ p r i o r (1.3) \hat{c} = argmax_{c \in C}\overbrace{P(d|c)}^{\rm likelihood} \overbrace{P(c)}^{\rm prior} \tag{1.3} c^=argmaxc∈CP(d∣c) likelihoodP(c) prior(1.3)
将文档 d d d表示为一系列特征 f 1 , f 2 , . . . f n f_1,f_2,...f_n f1,f2,...fn: c ^ = a r g m a x c ∈ C P ( f 1 , f 2 , . . . f n ∣ c ) ⏞ l i k e l i h o o d P ( c ) ⏞ p r i o r (1.4) \hat{c} = argmax_{c \in C}\overbrace{P(f_1,f_2,...f_n|c)}^{\rm likelihood} \overbrace{P(c)}^{\rm prior} \tag{1.4} c^=argmaxc∈CP(f1,f2,...fn∣c) likelihoodP(c) prior(1.4)
然而,等式1.4还是很难直接计算:如果没有某些简化的假设,估计每一个可能的特征组合的概率(例如,每一个可能的单词和位置集)将需要大量的参数和不可思议的大训练集。朴素贝叶斯分类器因此做了两个简化假设。
-
词袋假设
词袋假设(bag of words assumption:position doesn’t matter)举例来说,单词“love”不管是文档中的第一个单词,第100个单词对于分类的结果都是没有影响的。 -
朴素贝叶斯假设
也就是条件独立假设(conditional independence assumption:words are conditionally independent of each other given the class), P ( f i ∣ c ) P(f_i|c) P(fi∣c)在给定类别 c c c的情况下是独立的,可以“naively”表示为乘积的形式: P ( f 1 , f 2 , . . . f n ) = P ( f 1 ∣ c ) P ( f 2 ∣ c ) . . . P ( f n ∣ c ) (1.5) P(f_1,f_2,...f_n) = P(f_1|c)P(f_2|c)...P(f_n|c) \tag{1.5} P(f1,f2,...fn)=P(f1∣c)P(f2∣c)...P(fn∣c)(1.5)
最后的朴素贝叶斯分类器等式为: c N B = a r g m a x c ∈ C P ( c ) ∏ f ∈ F P ( f ∣ c ) (1.6) c_{NB} = argmax_{c \in C}P(c)\prod_{f \in F}{P(f|c)} \tag{1.6} cNB=argmaxc∈CP(c)f∈F∏P(f∣c)(1.6)
训练朴素贝叶斯分类器
如何学习 P ( c ) P(c) P(c)和 P ( f i ∣ c ) P(f_i|c) P(fi∣c)呢?
- 对于先验概率 P ( c ) P(c) P(c),用每个c类的文档在训练集中所占的百分比来计算。其中, N c N_c Nc是训练集中 c c c类文档数, N d o c N_{doc} Ndoc是训练集文档总数。 P ^ ( c ) = N c N d o c (1.7) \hat P(c) = \frac{N_c}{N_{doc}} \tag{1.7} P^(c)=NdocNc(1.7)
- 对于概率 P ( f i ∣ c ) P(f_i|c) P(fi∣c),我们假设一个特征就是文档中单词的存在,也就是 P ( w i ∣ c ) P(w_i|c) P(wi∣c),将其计算为单词 w i w_i wi在类别 c c c的所有文档的所有单词中出现次数的比例。所以首先将类别 c c c中的所有文档串联到一个“大”的“类别 c c c”文档中,然后通过计算 w i w_i wi在这个大的串联文档中的频率进行最大似然估计。 P ^ ( w i ∣ c ) = c o u n t ( w i , c ) ∑ w ∈ V c o u n t ( w , c ) (1.8) \hat P(w_i|c) = \frac{count(w_i,c)}{\sum_{w\in V}count(w,c)} \tag{1.8} P^(wi∣c)=∑w∈Vcount(w,c)count(wi,c)(1.8)
注意这里的 V V V指的是所有类别中所有单词的 v o c a b u l a r y vocabulary vocabulary,而不是类别 c c c的。
测试朴素贝叶斯分类器
那么将朴素贝叶斯分类器应用到文本中,我们需要考虑单词的位置,只需简单地通过索引遍历文档中每个单词的位置: p o s t i o n s ← a l l w o r d p o s i t i o n s i n t e x t d o c u m e n t c N B = a r g m a x c ∈ C P ( c ) ∏ i ∈ p o s i t i o n s P ( w i ∣ c ) (1.9) postions \leftarrow {all\,word\,positions\,in\,text\,document}\\c_{NB} = argmax_{c \in C}P(c)\prod_{i \in positions}{P(w_i|c)} \tag{1.9} postions←allwordpositionsintextdocumentcNB=argmaxc∈CP(c)i∈positions∏P(wi∣c)(1.9)
为了避免下溢和计算更快,我们选择对数运算: c N B = a r g m a x c ∈ C l o g P ( c ) + ∑ i ∈ p o s i t i o n s l o g P ( w i ∣ c ) (1.10) c_{NB} = argmax_{c \in C}logP(c) + \sum_{i \in positions}log{P(w_i|c)} \tag{1.10} cNB=argmaxc∈ClogP(c)+i∈positions∑logP(wi∣c)(1.10)
完善
在最大似然估计训练的过程中有些问题需要关注下。假设我们试图在给定类别为 p o s i t i v e positive positive的情况下估计单词“fantastic”的可能性,但是假设没有同时包含单词“fantastic”又被归类为 p o s i t i v e positive positive的训练文档。也许“fantastic”这个词碰巧在 n e g a t i v e negative negative出现(讽刺地?)。在这种情况下,该特征的概率为零:
P ^ ( " f a n t a s t i c " ∣ p o s i t i v e ) = c o u n t ( " f a n t a s t i c " , p o s i t i v e ) ∑ w ∈ V c o u n t ( w , p o s i t i v e ) = 0 \hat P("fantastic"|positive) = \frac{count("fantastic",positive)}{\sum_{w \in V}count(w,positive)} = 0 P^("fantastic"∣positive)=∑w∈Vcount(w,positive)count("fantastic",positive)=0
但是由于朴素贝叶斯是所有特征概率“naively”乘积,上述的零概率就会导致整个的零概率。最简单的解决方法是 a d d − o n e ( L a p l a c e ) s m o o t h i n g add-one(Laplace) smoothing add−one(Laplace)smoothing。
P ^ ( w i ∣ c ) = c o u n t ( w i , c ) + 1 ∑ w ∈ V ( c o u n t ( w , c ) + 1 ) = c o u n t ( w i , c ) + 1 ∑ w ∈ V c o u n t ( w , c ) + V (1.11) \hat P(w_i|c) = \frac{count(w_i,c)+1}{\sum_{w \in V}(count(w,c)+1)} = \frac{count(w_i,c)+1}{\sum_{w \in V}count(w,c)+ \color{red}{V}} \tag{1.11} P^(wi∣c)=∑w∈V(count(w,c)+1)count(wi,c)+1=∑w∈Vcount(w,c)+Vcount(wi,c)+1(1.11)
另外,该如何处理出现在测试数据但不在训练数据 v o c a b u l a r y vocabulary vocabulary中的单词呢?对于这种未知单词 u n k n o w n w o r d s unknown words unknownwords的解决方法就是忽略掉它们——将它们从测试文本中移除。还有一类单词可以选择移除:停止词(stop word),也就是非常频繁的词如the和a。这里我们可以选择对训练集 v o c a b u l a r y vocabulary vocabulary进行频率排序,将前10-100中的词定义为停止词。或者也可以使用某个预定义停止词表。在大多数的文本分类应用中,前者这种方法更常见。然后停止词就会在训练文本和测试文本中全被移除就像它们从未出现过。

朴素贝叶斯分类器类型
根据对数据集 P ( f e a t u r e s ∣ l a b e l ) P(features|label) P(features∣label)分布的不同假设,朴素贝叶斯分类器可分为不同的类型,以下是三种常见的类型:
- 高斯朴素贝叶斯(Gausian Naive Bayes)
假设特征是连续值,且符合高斯分布,单个特征条件概率的计算公式为:
p ( x ∣ C k ) = 1 2 π σ k 2 e − ( v − μ k ) 2 2 σ k 2 p(x|C_k) = \frac{1}{\sqrt{2\pi{\sigma_k^2}}}e^{-\frac{(v-\mu_k)^2}{2\sigma_k^2}} p(x∣Ck)=2πσk21e−2σk2(v−μk)2 - 多项式朴素贝叶斯(Multinominal Naive Bayes)
假设特征由多项分布生成,单个特征条件概率的计算公式为(这也是用于文本分类经典朴素贝叶斯算法之一):
p ( x ∣ C k ) = ( Σ i x i ) ! ∏ i x i ! ∏ p k i x i p(x|C_k) = \frac{(\Sigma_ix_i)!}{\prod_ix_i!}\prod p_{ki}^{x_i} p(x∣Ck)=∏ixi!(Σixi)!∏pkixi
MultinomialNB分布参数由每个类别 c c c的 θ c = ( θ c 1 , θ c 2 , θ c 3 , . . . θ c n ) \theta_c=(\theta_{c_1},\theta_{c_2},\theta_{c_3},...\theta_{c_n}) θc=(θc1,θc2,θc3,...θcn)向量决定,其中 n n n是特征的数量(对于文本分类是词汇量的大小), θ c i \theta_{c_i} θci是样本中属于类 c c c中特征 i i i概率 P ( x i ∣ c ) P(x_i|c) P(xi∣c)。参数 θ c \theta_c θc使用平滑过的最大似然估计法来估计,即相对频率计数,也就是上述的内容不再赘述。 - 伯努利朴素贝叶斯(Bernoulli Naive Bayes)
假设特征是独立的布尔模型,单个特征条件概率的计算公式为:
p ( x ∣ C k ) = ∏ i = 1 n p k i x i ( 1 − p k i ) ( 1 − x i ) p(x|C_k) = \prod^n_{i=1} p_{ki}^{x_i}(1-p_{ki})^{(1-x_i)} p(x∣Ck)=i=1∏npkixi(1−pki)(1−xi)
情感分析中的优化
尽管标准的朴素贝叶斯文本分类对于情感分析已经表现不错,但仍可对原始算法进行某些改进使之表现更佳,下面进行举例。
-
对于情感分析和许多文本分类任务来说,一个单词是否出现比它出现的次数多少更为重要。因此,可以通过将每篇文本中的单词计数减为1(clip the word counts in each document at 1)来提高性能,这种也叫做二类多项朴素贝叶斯(binary multinominal naive Bayes or binary NB)。与朴素贝叶斯唯一的不同是将类别 c c c中的所有文档串联到一个“大”的“类别 c c c”文档之前,先把每个文档的重复词去掉。如下图所示。
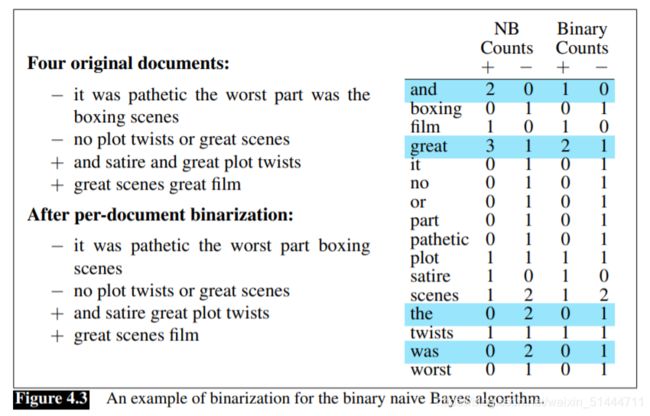
-
在做情感分析的文本分类时,一个非常简单的处理否定词的基准(baseline)就是:文本正则化时,在逻辑否定标志词(n’t,not,no,never)后的每个词加上前缀*NOT_*直到出现。所以 d i d n t l i k e t h i s m o i v e , b u t I didnt\,like\,this\,moive,but\,I didntlikethismoive,butI变成 d i d n t N O T _ l i k e N O T _ t h i s N O T _ m o v i e , b u t I didnt\,NOT\_like\,NOT\_this\,NOT\_movie,but\,I didntNOT_likeNOT_thisNOT_movie,butI
因此,新形成的“单词”,比如“NOT_like”、“NOT_recommend”,会更多地出现在负面文档中,成为负面情绪的线索,而像“NOT_bored”、“NOT_dismiss”这样的单词会成为正面情绪的线索。虽然句法解析以更准确地处理这些否定词和它们所修改的谓词之间的范围关系,但是这个简单的基线在实践中已经工作得很好。 -
在某些情况下我们可能没有充足的标注训练数据来训练准确的朴素贝叶斯分类器,可以利用情感词典(sentiment lexicons,)生成正面情绪和负面情绪的词。有四个比较流行的词典:General Inquirer(Stone et al.,1966)、LIWC(Pennebaker et al.,2007)、Hu和Liu(2004)的opinion lexicon还有MPQA Subjectivity Lexicon(Wilson et al.,2005)。
例如,MPQA主观性词汇有6885个词,2718个阳性词和4912个阴性词,每个词都标记为强偏差或弱偏差(这些词汇是可以自动学习的)。举例MPQA词典中一些积极和消极的词汇包括:+ : admirable, beautiful, confident, dazzling, ecstatic, favor, glee, great − : awful, bad, bias, catastrophe, cheat, deny, envious, foul, harsh, hate
延伸
在看朴素贝叶斯法的时候常看到贝叶斯估计等,实际上他们是不同的概念。整理参考https://www.cnblogs.com/HuZihu/p/9549479.html。
频率派 vs 贝叶斯派
-
Frequentist: Parameters are fixed
♦ Data are a repeatable random sample——there is a frequency
♦ Underlying parameters remain constant during this repeatable process -
Bayesian:Data are fixed
♦ Data are observed from the realized sample
♦ Parameters are unknown and described probabilistically

-
MLE:就是给定参数的情况下看到样本集的概率,从而最大化 P ( D ∣ 参 数 ) P(D|参数) P(D∣参数)
-
MAP:最大化 P ( 参 数 ∣ D ) P(参数|D) P(参数∣D)
-
Bayesian:预测时考虑所有可能的参数(参数的分布)
频率派:最大似然估计
首先介绍下似然函数。对于 P ( x ∣ θ ) P(x|\theta) P(x∣θ),若 θ \theta θ已知, x x x为变量,则此函数为概率函数(probabilty function);若 x x x已知, θ \theta θ为变量,则此函数为似然函数(likelihood function)。所以似然(likelihood)和概率(probability)表示的意义是完全不同的 ———— 在给定参数值的情况下,概率是用于描述未来出现某种情况的观测数据的可信度;在给定观测数据的情况下,似然用于描述参数值的可信度。

♦ MLE属于频率派,认为存在唯一真值 θ \theta θ。
♦ MLE只适用于数据量大的情况。如果数据量小,结果很可能产生偏差。举个简单的例子,假如把一个均匀的硬币抛10次,有7次正面朝上,3次反面朝上(假设数据服从伯努利分布)。那么这个伯努利概率分布函数就是 P ( D ∣ H e a d ) = P ( H e a d ) 7 ∗ ( 1 − P ( H e a d ) ) 3 P(D|Head)=P(Head)7*(1-P(Head))3 P(D∣Head)=P(Head)7∗(1−P(Head))3,函数在 P ( H e a d ) = 0.7 P(Head)=0.7 P(Head)=0.7时达到最大。那么我们能说 P ( H e a d ) = 0.7 P(Head)=0.7 P(Head)=0.7吗?这个结果肯定不准,因为我们都知道 P ( H e a d ) = P ( T a i l ) = 0.5 P(Head)=P(Tail)=0.5 P(Head)=P(Tail)=0.5。但是如果我们把这个硬币抛1000次,得出的结果就会较准确了。但是现实中很多时候无法做那么多次实验。
并且MLE不会把先验知识考虑进去,这样也很容易造成过拟合现象。比如对癌症的估计,一个医生一天可能接到了100名患者,但最终被诊断出癌症的患者为5个人,在MLE的模式下我们得到的得到癌症的概率为0.05。这显然是不太切合实际的,因为我们根据已有的经验,知道这种概率会低很多。然而MLE并没有把这种知识融入到模型里。
贝叶斯派:最大后验估计
♦ 通过上面的推导可以发现,MAP和MLE最大的不同在于 P ( θ ) P(\theta) P(θ)项,所以可以说MAP正好可以解决缺乏先验知识的缺点。这里 P ( θ ) P(\theta) P(θ)项正好起到了正则化的作用,如:若假设 P ( θ ) P(\theta) P(θ)服从高斯分布,则相当于加了个L2 norm;若假设 P ( θ ) P(\theta) P(θ)服从拉普拉斯分布,则相当于加了个L1 norm。
贝叶斯派:贝叶斯估计
♦ Bayesian属于贝叶斯派,认为 θ \theta θ是一个随机变量,符合一定的概率分布。
♦ MLE和MAP只会给出一个最优的解, 然而贝叶斯模型会给出对参数的一个分布,比如对模型的参数, 假定参数空间里有参数1,参数2, 参数3,…参数N,贝叶斯模型学出来的就是这些参数的重要性(也就是分布),然后当我们对新的样本预测的时候,就会让所有的模型一起去预测,但每个模型会有自己的权重(权重就是学出来的分布)。最终的决策由所有的估计根据其权重做出决策。
♦ 可以看到贝叶斯的核心就是要近似的计算 P ( θ ∣ D ) P(\theta|D) P(θ∣D),那这个积分是很复杂的。

一种解决方法就是使用蒙特卡洛算法。比如我想计算一个公司所有员工的平均身高,这个时候最简答粗暴的方法就是让行政去一个一个去测量,然后计算平均值。但想计算所有中国人的平均身高,怎么做?(显然一个个测量是不可能的)即采样。我们随机的选取一些人测量他们的身高,然后根据他们的身高来估计全国人民的审稿。当然采样的数目越多越准确,采样的数据越有代表性越准确。
再例:假设我们不知道π,但是想计算圆的面积。也可以通过采样的方法近似得到。随机再下图所示的正方形中撒入一些点,记落入红色区域的点的个数为 n 1 n_1 n1,落入白色区域的个数为 n 2 n_2 n2,则四分之一圆的面积就为 n 1 / ( n 1 + n 2 ) n_1/(n_1+n_2) n1/(n1+n2)。—————— 蒙特卡洛思想
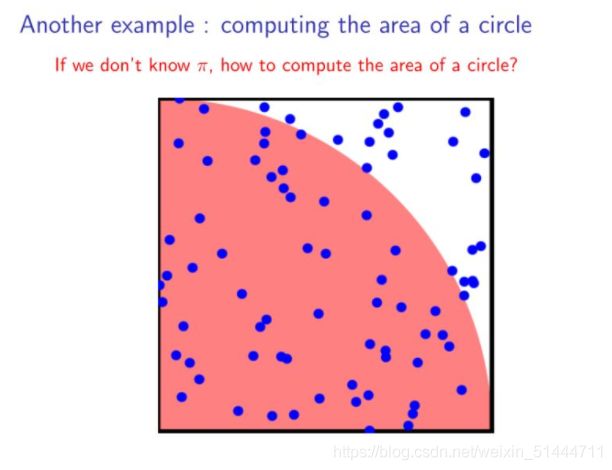
那如何对连续函数估计呢?采样 n n n多个数据,逼近最后的积分值。

假设我们要计算 f ( x ) f(x) f(x)的期望值, 我们也有 p ( x ) p(x) p(x)这种分布,这个时候我们就可以不断的从 p ( x ) p(x) p(x)这个分布里做一些采样,比如 x 1 , x 2 , . . . x n x_1,x_2,...x_n x1,x2,...xn, 然后用这些采样的值去算 f ( x ) f(x) f(x), 所以最后得到的结果就是 ( f ( x 1 ) + f ( x 2 ) . . . + f ( x n ) ) / n (f(x_1) + f(x_2)... + f(x_n))/n (f(x1)+f(x2)...+f(xn))/n
上面例子中提到的采样都是独立的。也就是每个样本跟其他的样本都是独立的,不影响彼此之间的采样。然而,在现实问题上,有些时候我们想加快有效样本的采样速度。这个问题讨论的就是怎么优化采样过程了,也是机器学习里一个比较大的话题了。
重申一下,用上面提到的采样方式我们可以去近似估计复杂的积分,也可以计算圆的面积,也可以计算全国人口的平均身高。但这个采样方式是独立的,有些时候,我们希望我们用更少的样本去更准确的近似某一个目标,所以就出现了sampling这种一个领域的研究,就是在研究以什么样的方式优化整个采样过程,使得过程更加高效。
♦ MCMC

每个采样的样本都是互相有关联性的。但是MCMC算法需要在整个数据集上计算。也就是说为了得到一个样本,需要用所有的数据做迭代。这样当N很大时,显然不适用。而且限制了贝叶斯方法发展的主要原因就是计算复杂度太高。因此现在贝叶斯领域人们最关心的问题是:怎么去优化采样,让它能够在大数据环境下学习出贝叶斯模型?
降低迭代复杂度的一个实例:
对于逻辑回归,使用梯度下降法更新参数时,有批量梯度下降法(即使用整个数据集去更新参数),为了降低计算复杂度,人们使用了随机梯度下降法,即随机从数据集中选取样本来更新参数。
所以,能否将此思想用于MCMC采样中呢?
Yes!langevin dynamic(MCMC算法中的一种),和stochastic optimizaiton(比如随机梯度下降法)可以结合在一起用。这样,我们就可以通过少量的样本去做采样,这个时候采样的效率就不在依赖于N了,而是依赖于m, m是远远小于N。

