pycharm动手学深度学习笔记-01预备知识

笔记参考：
B站橘子
CSDNpycharm版（简略版笔记）
核心的不懂的地方参考沐神的课程主页

本地python环境 python3.8
改成了深度学习专用的

预备知识

数据操作和数据预处理

dim啥意思查了一下

torch.cat((x,y),dim=0) :张量 X,Y按照列堆起来
torch.cat((x,y),dim=1) :张量 X,Y按照行并排起来

广播机制
具体看他如何填充的
tensor([[1, 2]])

1 2
1 2
1 2

tensor([[1],
[2],
[3]])

    1 1
    2 2 
    3 3

tensor([[2, 3],
[3, 4],
[4, 5]])
数据预处理

inputs = inputs.fillna(inputs.mean())  # 用均值填充NaN
print(inputs)
print(outputs

后面data 的iloc方法解释的很清楚。

inputs, outputs = data.iloc[:, 0: 2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean())  # 用均值填充NaN
print(inputs)
print(outputs)

切片搞明白之后
来看输出。
注意他的

data.iloc[:, 0: 2]

的区间 左开右闭。

data = pd.read_csv(datafile)  # 可以看到原始表格中的空值NA被识别成了NaN
print('1.原始数据:\n', data)

inputs, outputs = data.iloc[:, 0: 2], data.iloc[:, 2]
print(inputs)

运行结果的切片

1.原始数据:
    NumRooms Alley   Price
0       NaN  Pave  127500
1       2.0   NaN  106000
2       4.0   NaN  178100
3       NaN   NaN  140000
   NumRooms Alley
0       NaN  Pave
1       2.0   NaN
2       4.0   NaN
3       NaN   NaN

上面代码output的切片表示
所有行的第二列

切片搞明白之后看特征的提取

这一篇介绍的很详细。包括前后缀。

佬们这个函数 怎么感觉 顺序丝毫没有逻辑性 咋还能自动排序专科本科硕士呢

其实就是独热编码，顺序不要太纠结，上面的文档可以指定某个列。

print(df2.fillna(method='bfill', limit=2))  # 限制填充个数,
print(df2.fillna(method="ffill", limit=1, axis=1))  #

第一句话：用矩阵竖着来看后面的那个值来填充，限制个数 指的是：
限制连续填充了多少个，
连续填充的limit不能超过指定的值，
总数是可以的，
所以才会有代码里面的输出。

线性代数

A.sum(axis=0): tensor([40., 45., 50., 55.])
A.sum(axis=1): tensor([ 6., 22., 38., 54., 70.])

A: tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.],
        [12., 13., 14., 15.],
        [16., 17., 18., 19.]])
A.shape: torch.Size([5, 4])
A.sum(): tensor(190.)
A.sum(axis=0): tensor([40., 45., 50., 55.])
A.sum(axis=1): tensor([ 6., 22., 38., 54., 70.])

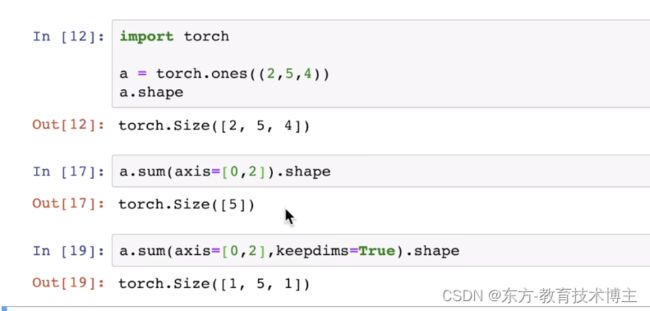
axis=0/1其实就是把二维数组沿着行的方向求和或者沿着列的方向求和

这个就是 axis来降维，axis写的是几，
shape的第几维度就变成1，所谓变成一，的意思就是 直接去掉，
所以称之为降维。
加入keepdims之后size变成1

向量的点积
关于torch.ones
这里面有线代本质的笔记
矩阵相乘，左列右行。

范数
代码：

print('9.范数')
u = torch.tensor([3.0, -4.0])
print('向量的2范数:', torch.norm(u))  # 向量的2范数
print('向量的1范数:', torch.abs(u).sum())  # 向量的1范数
v = torch.ones((4, 9))
print('v:', v)
print('矩阵的2范数:', torch.norm(v))  # 矩阵的2范数

运行结果
3和4的绝对值相加是7，
最后一个每个元素平方和是36，开根号以后就是6.

9.范数
向量的2范数: tensor(5.)
向量的1范数: tensor(7.)
v: tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1., 1., 1., 1.]])
矩阵的2范数: tensor(6.)

根据索引访问矩阵

print('10.根据索引访问矩阵')
y = torch.arange(10).reshape(5, 2)
print('y:', y)
index = torch.tensor([1, 4])
print('y[index]:', y[index])

根据索引访问矩阵
y: tensor([[0, 1],
        [2, 3],
        [4, 5],
        [6, 7],
        [8, 9]])
y[index]: tensor([[2, 3],
        [8, 9]])

没什么难点就是把第几行给打印出来了。

二维矩阵上gather()函数

顶级理解：

torch.gather的理解
index=[ [x1,x2,x3],
[y1,y2,y2],
[z1,z2,z3] ]

如果dim=0
填入方式
[ [(x1,0),(x2,1),(x3,2)]
[(y1,0),(y2,1),(y3,2)]
[(z1,0),(z2,1),(z3,2)] ]

如果dim=1
[ [(0,x1),(0,x2),(0,x3)]
[(1,y1),(1,y2),(1,y3)]
[(2,z1),(2,z2),(2,z3)] ]

理解pytorch中的max()和argmax()函数

argmax
max
返回最大值和索引。
链接里面的例子很容易懂。
item函数
本质是用索引
从tensor中
返回python的类型的数据

print('13.item()函数')
a = torch.Tensor([1, 2, 3])
print('a[0]:', a[0])  # 直接取索引返回的是tensor数据
print('a[0].item():', a[0].item())  # 获取python number

13.item()函数
a[0]: tensor(1.)
a[0].item(): 1.0

微积分

微分和积分是微积分的两个分支，前者可以应用于深度学习中的优化问题。

导数可以被解释为函数相对于其变量的瞬时变化率，它也是函数曲线的切线的斜率。

梯度是一个向量，其分量是多变量函数相对于其所有变量的偏导数。

链式法则使我们能够微分复合函数
似乎想明白了，记录一下我的理解：偏导矩阵的结构取决于我们如何约定摆放的位置。在相同的约定规则之下，由于Ax的偏导值：dy(i)/dx(j)
= Ai,j与x^TA的偏导值：dy(i)/dx(j) = Aj,i在行列上刚好相反，因此它俩的矩阵结构必定互为转置。这样的约定有利于我们在形式上实现一个统一的函数f(i,j)，用来计算dy(i)/dx(j)的偏导结果

找个数学大佬问清楚，留个坑。
填坑：
微信群gordon大佬给手算了一下

G佬

这不高等代数里面的 nubla算子吗，然后组成向量的形式

自动求导

torch.dot 函数：与 NumPy 的 dot 不同，torch.dot 有意仅支持计算两个具有相同数量元素的 1D 张量的点积。

知乎：Pytorch autograd,backward详解
大佬手写的很详细，基本上能看到。评论区的讨论质量也很不错，
不得不说知乎的社区氛围是要比CSDN高一个层次的。
用大佬的话说：

我们再仔细想想，对z求和不就是等价于z 点乘一个相同维度的全为1的矩阵吗？即 ,而这个I也就是我们需要传入的grad_tensors参数。(点乘只是相对于一维向量而言的，对于矩阵或更高为的张量，可以看做是对每一个维度做点乘
说了这么多，grad_tensors的作用其实可以简单地理解成在求梯度时的权重，因为可能不同值的梯度对结果影响程度不同，所以pytorch弄了个这种接口，而没有固定为全是1。引用自知乎上的一个评论：如果从最后一个节点(总loss)来backward，这种实现(torch.sum(y*w))的意义就具体化为 multiple loss term with difference weights 这种需求了吧。

代码如下：

import torch

print('1.自动梯度计算')
x = torch.arange(4.0, requires_grad=True)  # 1.将梯度附加到想要对其计算偏导数的变量
print('x:', x)
print('x.grad:', x.grad)
y = 2 * torch.dot(x, x)  # 2.记录目标值的计算 计算点积
print('y:', y)
y.backward()  # 3.执行它的反向传播函数
print('x.grad:', x.grad)  # 4.访问得到的梯度
print('x.grad == 4*x:', x.grad == 4 * x)

## 计算另一个函数
x.grad.zero_()
y = x.sum()
print('y:', y)
y.backward()
print('x.grad:', x.grad)

# 非标量变量的反向传播
#为什么要有非标量，因为矩阵会报错 详见知乎
x.grad.zero_()
print('x:', x)
y = x * x
y.sum().backward()
print('x.grad:', x.grad)


def f(a):
    b = a * 2
    print('b.norm')
    print(b.norm)
    while b.norm() < 1000:  # 求L2范数：元素平方和的平方根
        print(b.norm())
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c


print('2.Python控制流的梯度计算')
a = torch.tensor(2.0)  # 初始化变量 初值为2 的标量
a.requires_grad_(True)  # 1.将梯度赋给想要对其求偏导数的变量
print('a:', a)
d = f(a)  # 2.记录目标函数
print('d:', d)
d.backward()  # 3.执行目标函数的反向传播函数
#公式 相当于是  f（x）= 512x
print('a.grad:', a.grad)  # 4.获取梯度

运行结果：

1.自动梯度计算
x: tensor([0., 1., 2., 3.], requires_grad=True)
x.grad: None
y: tensor(28., grad_fn=<MulBackward0>)
x.grad: tensor([ 0.,  4.,  8., 12.])
x.grad == 4*x: tensor([True, True, True, True])
y: tensor(6., grad_fn=<SumBackward0>)
x.grad: tensor([1., 1., 1., 1.])
x: tensor([0., 1., 2., 3.], requires_grad=True)
x.grad: tensor([0., 2., 4., 6.])
2.Python控制流的梯度计算
a: tensor(2., requires_grad=True)
b.norm
<bound method Tensor.norm of tensor(4., grad_fn=<MulBackward0>)>
tensor(4., grad_fn=<CopyBackwards>)
tensor(8., grad_fn=<CopyBackwards>)
tensor(16., grad_fn=<CopyBackwards>)
tensor(32., grad_fn=<CopyBackwards>)
tensor(64., grad_fn=<CopyBackwards>)
tensor(128., grad_fn=<CopyBackwards>)
tensor(256., grad_fn=<CopyBackwards>)
tensor(512., grad_fn=<CopyBackwards>)
d: tensor(1024., grad_fn=<MulBackward0>)
a.grad: tensor(512.)