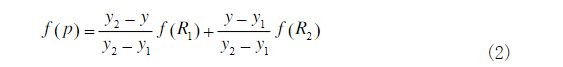python数字图像处理笔记07 双线性插值法 ~~~这就是为什么要学数学的例子！

大家都是怎么学习图像处理，这些公式和图形，有什么书能讲解这些知识？推荐一些吧！！！！

单线性插值

已知P1点和P2点，坐标分别为(x1, y1)、(x2, y2)，要计算 [x1, x2] 区间内某一位置 x 在直线上的y值

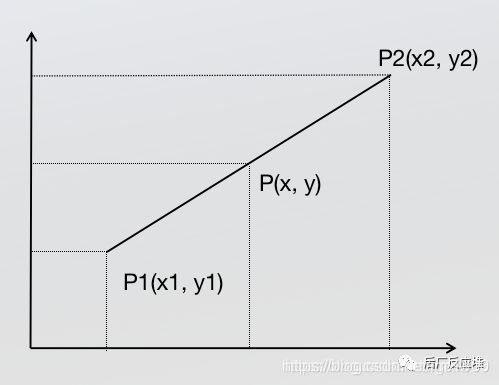
2点求一条直线公式

由于 x 值已知，所以可以从公式得到 y 的值

已知 y 求 x 的过程与以上过程相同，只是 x 与 y 要进行交换。

由于像素间距离 x2-x1=1

所以设 a=x2-x 那么 x-x1=1-a;

y=ay1+(1-a)y2

双线性插值

在两个方向分别进行一次线性插值。

我们以一个例子来介绍双线性插值原理:假如我们想得到未知函数f在点P=f(x, y)的值,设f在Q11=(x1, y1),Q12=(x1, y2),Q21=(x2,y1),Q22=(x2,y2)四个点的值。

首先在x方向上面线性插值，得到R2、R1：

然后以R2,R1在y方向上面再次线性插值：

这样就得到所要的结果 f(x, y)

因为双线性插值只会使用相邻的4个点，因此分母总是为1，故可以约去；那么插值公式就可以化简为

由于插值点不一定是整数，例如点（1.2, 3.4），其相邻的四个点分别为(1,3),(2,3),(1,4),(2,4)；故可设插值点(x,y)由（i+u,j+v）点表示，其中的u，v为坐标的小数部分，取值为[0,1)。写成 f(i+u,j+v)的形式，则 u=0.2,v=0.4, i=1, j=3

可知其相邻点坐标分别为(i,j)、(i,j+1)、(i+1,j)、(i+1,j+1)四点。可得

例

给定一个矩阵（图片本身就是一种矩阵），将1个 3 ∗ 3 尺寸的矩阵使用最近邻插值法到 4 ∗ 4

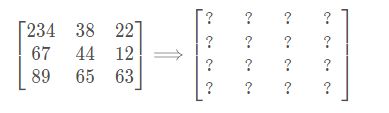
源图像与目标图像坐标的对应关系如下式

dst[0,1]对应的src位置如下：

src_x = 0 * (3 / 4) = 0
src_y = 1 * (3 / 4) = 0.75
u=0,v=0.75

得到的对应于源图的坐标是（0 , 0.75）, 这其实只是一个概念上的虚拟象素,实际在源图中并不存在这样一个象素,那么目标图的象素（0，1）的取值不能够由这个虚拟象素来决定，而只能由源图的这四个象素共同决定：（0，0）（0，1）（1，0）（1，1），
而由于（0,0.75）离（1，0）要更近一些，那么（1,0）所起的决定作用更大一些。

dst[0,1]=(1−0)(1−0.75)∗src[1,1]+(1−0)∗0.75∗src[1,0]+0∗(1−0.75)∗src[0,1]+0∗0.75∗src[0,0]
= 11 + 50 = 61

算法优化（待了解）

源图像和目标图像几何中心的对齐

SrcX=(dstX+0.5) * (srcWidth/dstWidth) -0.5

SrcY=(dstY+0.5) * (srcHeight/dstHeight)-0.5

代码实现

图像中的每个值都是通过双线性插值的方法得到的，首先生成一个空的目标图像大小的矩阵，然后往里面填值。

计算在源图上四个近邻点的位置

src_x = (dst_x + 0.5) * scale_x - 0.5
src_y = (dst_y + 0.5) * scale_y - 0.5

计算在源图上四个近邻点的位置

src_x_0 = int(np.floor(src_x))
src_y_0 = int(np.floor(src_y))
src_x_1 = min(src_x_0 + 1, src_w - 1)
src_y_1 = min(src_y_0 + 1, src_h - 1)

def bl_interpolate2(src , ax=1., ay=1.):
    src_h, src_w, C = src.shape

    # 目标图像宽高
    dst_h = int(ay * src_h)
    dst_w = int(ax * src_w)

    # dst_w, dst_h = new_size # 目标图像宽高
    # src_h, src_w = src.shape[:2] # 源图像宽高
    if src_h == dst_h and src_w == dst_w:
        return src.copy()
    scale_x = float(src_w) / dst_w # x缩放比例
    scale_y = float(src_h) / dst_h # y缩放比例

    # 遍历目标图像，插值
    dst = np.zeros((dst_h, dst_w, 3), dtype=np.uint8)
    for n in range(3): # 对channel循环
        for dst_y in range(dst_h): # 对height循环
            for dst_x in range(dst_w): # 对width循环
                # 目标在源上的坐标
                src_x = (dst_x + 0.5) * scale_x - 0.5
                src_y = (dst_y + 0.5) * scale_y - 0.5
                # 计算在源图上四个近邻点的位置
                src_x_0 = int(np.floor(src_x))
                src_y_0 = int(np.floor(src_y))
                src_x_1 = min(src_x_0 + 1, src_w - 1)
                src_y_1 = min(src_y_0 + 1, src_h - 1)

                # 双线性插值
                value0 = (src_x_1 - src_x) * src[src_y_0, src_x_0, n] + (src_x - src_x_0) * src[src_y_0, src_x_1, n]
                value1 = (src_x_1 - src_x) * src[src_y_1, src_x_0, n] + (src_x - src_x_0) * src[src_y_1, src_x_1, n]
                dst[dst_y, dst_x, n] = int((src_y_1 - src_y) * value0 + (src_y - src_y_0) * value1)
    return dst
    
# 输出图片    
out = bl_interpolate2(img, ax=1.5, ay=1.5)
XImage.imShow(out, self.lb2)

图像处理100问例子

def bl_interpolate(img, ax=1., ay=1.):
    H, W, C = img.shape

    aH = int(ay * H)
    aW = int(ax * W)

    # get position of resized image
    y = np.arange(aH).repeat(aW).reshape(aW, -1)
    x = np.tile(np.arange(aW), (aH, 1))

    # get position of original position
    y = (y / ay)
    x = (x / ax)

    ix = np.floor(x).astype(np.int)
    iy = np.floor(y).astype(np.int)

    ix = np.minimum(ix, W-2)
    iy = np.minimum(iy, H-2)

    # get distance
    dx = x - ix
    dy = y - iy

    dx = np.repeat(np.expand_dims(dx, axis=-1), 3, axis=-1)
    dy = np.repeat(np.expand_dims(dy, axis=-1), 3, axis=-1)

    # interpolation
    out = (1-dx) * (1-dy) * img[iy, ix] + dx * (1 - dy) * img[iy, ix+1] + (1 - dx) * dy * img[iy+1, ix] + dx * dy * img[iy+1, ix+1]

    out = np.clip(out, 0, 255)
    out = out.astype(np.uint8)

    return out

参考链接:https://zhuanlan.zhihu.com/p/49832048
参考链接:https://blog.csdn.net/siyue0211/article/details/92660001
参考链接:https://blog.csdn.net/m0_37799466/article/details/103890049