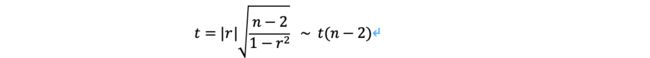相关性分析

1、方差分析

参考：https://zhuanlan.zhihu.com/p/99123384

方差分析（analysis of variance）：检验多个总体均值是否相等，研究一个或多个分类型自变量对一个数值型应变量的影响。

1.1、相关术语：

• 因素/因子：检验的对象
• 水平/处理：因素的不同表现
• 观测值：每个因子水平下的样本数据
• 总平方和SST：是全部观测值与总均值的误差平方和
• 组间平方和SSA：是各组均值与总均值的误 差平方和，反映各样本均值之间的差异程度
• 组内平方和SSE：是每个水平的样本数据与其组均值的误差平方和，反映了随机误差的大小
• 组间均方/组间方差MSA：等于SSA/(k-1)，k为因素水平的个数
• 组内均方/组内方差MSE：等于SSE/(n-k)，n为全部观测值的个数
• 判定系数R² = SSA/SST ，用来衡量自变量与因变量的关系强度

1.2、方差分析基本假定：

每个总体相互独立且都服从正态分布，各个总体的方差相同。

1.3、原理：

方差分析，听名字就知道，需要考察分析数据误差的来源。

组内误差SSE，是水平内部的误差，是抽样的随机性造成的随机误差。它放映了除自变量的影响之外，其他因素对因变量的总影响，因此也称为残差变量。

组间误差SSA，是不同水平间的误差，既可能是抽样的随机性造成的随机误差，也可能是各水平间的系统性因素造成的系统误差。它放映了自变量对因变量的影响，也称为自变量效应或因子效应。

总误差SST=组内误差SSE+组间误差SSA，反应了全部观测值的离散状况。

如果不同的水平对于因变量的没有影响，那么组间误差就只包括随机误差，而没有系统误差。此时，组间误差与组内误差的均方（方差）就应该非常接近，其比值接近1。反之，如果不同的水平对于因变量有影响，它们均方比值会大于1。

1.4、实例：

为了对几个行业的服务质量进行评价，消费者协会在零售业、旅游业、航空公司、家电制造业分别抽取了不同的企业作为样本。其中零售业抽取7家，旅游业抽取6家，航空公司抽取5家，家电制造业抽取5家。每个行业中所抽取的这些企业，假定它们在服务对象、服务内容、企业规模等方面基本上是相同的。然后统计出最近一年中消费者对总共23家企业投诉的次数，结果如下表所示。
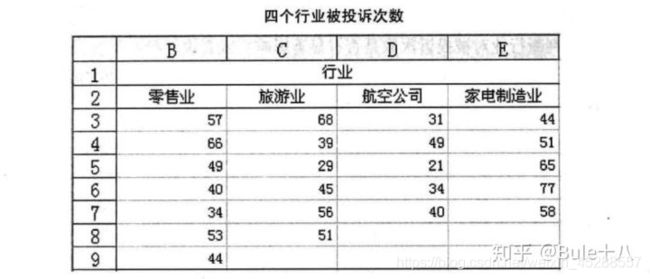在上面的实例中，行业是要检验的对象，称为因素或因子；零售业、旅游业、航空公司、家电制造业是行业这一因素的具体变现，称为水平或处理；每个行业下得到的样本数据称为观测值。该实例为单因素4水平试验。因素的每一个水平是一个总体，如零售业、旅游业、航空公司、家电制造业可以看成4个总体，上面的数据是从这4个总体中抽取的样本数据。

单因素方差分析中，涉及两个变量：分类型自变量，数值型因变量。该实例中，要研究行业对被投诉次数是否有影响，这里的分类型数据行业就是自变量，数字型数据被投诉次数就是因变量。

1.4.1、解题第一步：提出假设

设：1-零售业、2-旅游业、3-航空公司、4-家电制造业

H₀：μ₁=μ₂=μ₃=μ₄，行业对被投诉次数没有显著影响

H₁：μ₁、μ₂、μ₃、μ₄不全相等，行业对被投诉次数有显著影响

1.4.2、解题第二步：构造检验统计量

• （1）计算各误差平方：
  总平方和SST = (57-47.869565)²+(66-47.869565)²+…+(58-47.869565)² =4164.608696
  组间平方和SSA = 7*(49-47.869565)²+6*(48-47.869565)²
  +5*(35-47.869565)²+5*(59-47.869565)²
  =1456.608696
  组内平方和SSE = (57-49)²+(66-49)²+…+(44-49)²+ (68-48)²+(39-48)²+…+(51-48)²+ (31-35)²+(49-35)²+…+(40-35)²+ (44-59)²+(51-59)²+…+(58-59)²
  = 2708
  上面得出的结果也可以验证：SST = SSA+SSE

• （2）计算统计量：
  由于各误差平方和的大小与观测值的多少有关，为消除观测值多少对误差平方和大小的影响，需要将其平均，也就是用各平方和除以它们所对应的自由度，这一结果称为均方，也称方差。
  由于是要比较组间均方和组内均方之间的差异，所以只需计算SSA和SSE的均方。
  MSA = SSA/(k-1) = 1456.608696/(4-1) = 485.536232
  MSE = SSE/(n-k) = 2708/(23-4) = 142.526316
  H₀为真时，则表示每个样本都是来自于均值为μ，方差为σ²的同一个正态总体，则
  MSA/σ² ~ ²(k-1)
  MSE/σ² ~ ²(n-k)
  进一步得到F = MSA/MSE ~ F(k-1,n-k)
  计算结果F = MSA/MSE = 3.406643

1.4.3、解题第三步：统计决策

取显著性水平 =0.05，F₀₀₅(3，19)=3.13

由于F>F₀₀₅，因此拒绝原假设H₀，即认为行业对被投诉次数有明显影响

1.4.4、解题第四步：关系强度测量

R² = SSA/SST = 1456.608696/4164.608696=34.98%

R = 0.59

行业对被投诉次数的影响效应占总效应的34.98%，残差效应则占65.02%。R = 0.59，表明行业与被投诉次数之间有中等以上的关系。

2、相关与回归分析

参考：https://zhuanlan.zhihu.com/p/99123384

数值型自变量与数值型因变量之间的分析方法，相关与回归分析。

2.1、相关分析

相关关系就是对两个变量间线性关系的描述与度量。

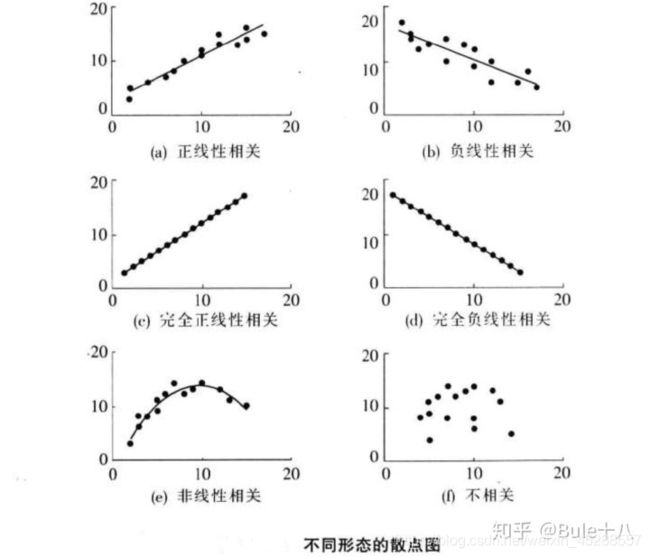
2.1.1 、散点图

绘制散点图来判断变量之间的关系形态

2.1.2、相关系数

相关系数（correlation coefficient）是根据样本数据计算的度量两个变量之间线性关系强度的统计量。

r = Cov(x,y) / σᵪσ ，也称线性相关系数或Pearson相关系数

2.1.3、显著性校验

对相关系数进行显著性校验，以判断样本所反应的关系是否能够代表两个变量总体的关系，具体步骤如下:

2.1.3.1、提出假设：

H₀：ρ=0(ρ总体相关系数)，即两个变量没有线性相关性

H₁：ρ<>0

2.1.3.2、计算统计量：

2.1.3.3、进行决策：

上面计算的t值与显著性水平 对应的t值比较

2.2、回归分析

回归分析侧重于考察变量间的数量关系，并通过数学表达式将这种关系表达出来。

2.2.1 、一元线性回归

回归模型： = β₀+β₁ +ε

β₀+β₁ 反映了由于 的变化而引起的 的线性变化；ε是被称为误差项的随机变量，放映了除 和 之间的线性关系之外的随机因素对 的影响。

…

根据样本数据拟合回归方程时，实际上已经假定变量x与y之间存在着线性关系，即y=β₀+β₁ +ε，并且假定误差项ε是一个服从正态分布的随机变量，且对不同的x具有相同的方差。

回归方程：E( )= β₀+β₁

2.2.1.1 、估算回归方程

利用最小二乘法使因变量的观测值yᵢ与估计值ŷᵢ的离差平方和达到最小，用来估计回归模型参数β₀和β₁。

2.2.1.2、直线的拟合优度

1）判定系数R²，测度回归直线对观测数据的拟合程度。

总平方SST = ∑(yᵢ-ȳ)²
∑(yᵢ-ȳ)² = ∑(ŷ-ȳ)²+∑(yᵢ-ŷ)²+2∑(ŷ-ȳ)(yᵢ-ŷ)
由于，2∑(ŷ-ȳ)(yᵢ-ŷ)=0，则
∑(yᵢ-ȳ)² = ∑(ŷ-ȳ)²+∑(yᵢ-ŷ)²

总平方和(SST) = 回归平方和(SSR)+残差平方和(SSE)

回归平方和SSR，∑(ŷ-ȳ)²放映了x与y之间的线性关系引起的y的变化，是可以由回归直线来解释的yᵢ的变差部分。

残差平方和/误差平方和SSE，∑(yᵢ-ŷ)²是不能由回归直线解释的yᵢ的变差部分。

判定系数R² = SSR/SST

2）估计的标准误差 ，反映了用估计的回归方程预测因变量y时预测误差的大小，是对误差项ε的标准差的估计，可以看做是在排除x对y的线性影响后，y随机波动大小的一个估计量。

= √SSE/n-2 = √MSE

2.2.1.3、显著性检验

1）线性关系检验

H₀：β₁=0,两个变量之间的线性关系不显著，则

2）回归系数检验

检验自变量对因变量的影响是否显著，一元线性回归中，检验β₁是否为0。

回归系数β₁的抽样分布服从正态分布

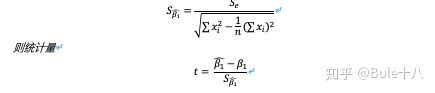
*在一元线性回归中，上面的F检验和检验等价。但是在多元回归分析中，F检验是用来检验总体回归关系的显著性，t检验则是检验各个回归系数的显著性。

3、简单相关性分析(两个连续型变量)

参考：https://zhuanlan.zhihu.com/p/36441826

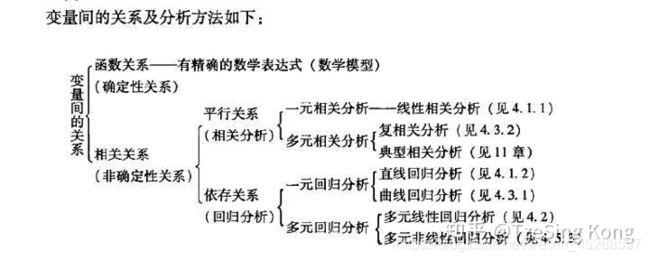
3.1、变量间的关系分析

变量之间的关系可分为两类：

• 存在完全确定的关系——称为函数关系
• 不存在完全确定的关系——虽然变量间有着十分密切的关系，但是不能由一个或多各变量值精确地求出另一个变量的值，称为相关关系，存在相关关系的变量称为相关变量

相关变量的关系也可分为两种：

• 两个及以上变量间相互影响——平行关系
• 一个变量变化受另一个变量的影响——依存关系

它们对应的分析方法：

• 相关分析是研究呈平行关系的相关变量之间的关系
• 回归分析是研究呈依存关系的相关变量之间的关系

回归分析和相关分析都是研究变量之间关系的统计学课题，两种分析方法相互结合和渗透

3.2、简单相关分析

• 相关分析：就是通过对大量数字资料的观察，消除偶然因素的影响，探求现象之间相关关系的密切程度和表现形式
• 主要研究内容：现象之间是否相关、相关的方向、密切程度等，不区分自变量与因变量，也不关心各变量的构成形式
• 主要分析方法：绘制相关图、计算相关系数、检验相关系数

3.2.1、计算两变量之间的线性相关系数

所有相关分析中最简单的就是两个变量间的线性相关，一变量数值发生变动，另一变量数值会随之发生大致均等的变动，各点的分布在平面图上大概表现为一直线。
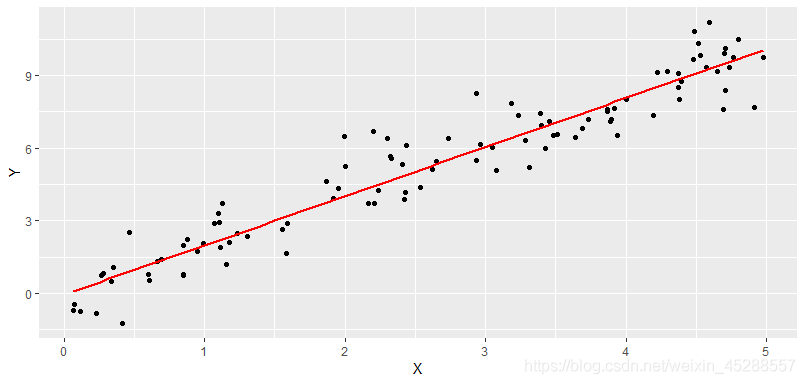线性相关分析，就是用线性相关系数来衡量两变量的相关关系和密切程度

例子：研究身高与体重的关系

import numpy as np
import matplotlib.pyplot as plt
x = np.array([171,175,159,155,152,158,154,164,168,166,159,164])
y = np.array([57,64,41,38,35,44,41,51,57,49,47,46])

xishu=np.corrcoef(x, y)
print(xishu)
plt.scatter(x, y)
plt.show()

结果：

array([[1.        , 0.95930314],
       [0.95930314, 1.        ]])

3.2.2、相关系数的假设检验

在 R语言 中有 cor.test() 函数

# r的显著性检验,参数alternative默认是"two.side"即双侧t检验
# method默认"pearson"
> cor.test(x1, x2)


	Pearson's product-moment correlation

data:  x1 and x2
t = 10.743, df = 10, p-value = 8.21e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.8574875 0.9888163
sample estimates:
      cor 
0.9593031

4、多变量相关性分析(一个因变量与多个自变量)

参考：https://zhuanlan.zhihu.com/p/37605060

4.1、前言：

继上一篇文章，继续探讨相关性分析，这次不再是两个变量，而是3个或者以上的变量之间的相关关系分析。

4.2、偏相关或复相关

简单相关：研究两变量之间的关系

偏相关或复相关：研究三个或者以上变量与的关系

在这里仍然是选择最简单的线性相关来解释。

4.3、意义与用途：

有些情况下，我们只想了解两个变量之间是否有线性相关关系，并不想拟合建立它们的回归模型，也不需要区分自变量和因变量，这时可用相关性分析。

4.4、分析方法：

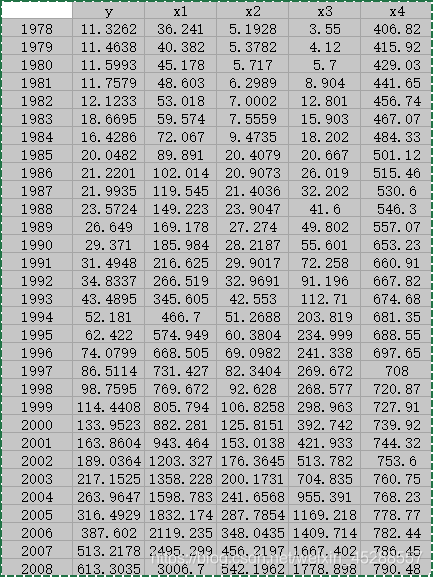
4.4.1、样本相关阵

例子：

> X <- read.table("clipboard", header = T)
> cor(X)  # 相关系数矩阵
           y        x1        x2        x3        x4
y  1.0000000 0.9871498 0.9994718 0.9912053 0.6956619
x1 0.9871498 1.0000000 0.9907018 0.9867664 0.7818066
x2 0.9994718 0.9907018 1.0000000 0.9917094 0.7154297
x3 0.9912053 0.9867664 0.9917094 1.0000000 0.7073820
x4 0.6956619 0.7818066 0.7154297 0.7073820 1.0000000

再看看矩阵散点图：

> pairs(X, ...)  # 多元数据散点图

相关系数检验：

> install.package('psych')  # 先安装一个'psych'的包
> library(psych)
> corr.test(X)

Call:corr.test(x = yX)
Correlation matrix 
      y   x1   x2   x3   x4
y  1.00 0.99 1.00 0.99 0.70
x1 0.99 1.00 0.99 0.99 0.78
x2 1.00 0.99 1.00 0.99 0.72
x3 0.99 0.99 0.99 1.00 0.71
x4 0.70 0.78 0.72 0.71 1.00
Sample Size 
[1] 31
Probability values (Entries above the diagonal are adjusted for multiple tests.) 
   y x1 x2 x3 x4
y  0  0  0  0  0
x1 0  0  0  0  0
x2 0  0  0  0  0
x3 0  0  0  0  0
x4 0  0  0  0  0

 To see confidence intervals of the correlations, print with the short=FALSE option

4.4.2、复相关分析

https://zhuanlan.zhihu.com/p/55240092

4.4.3、决定系数 R²

https://zhuanlan.zhihu.com/p/55240092

在 线性回归 中的 3.4 决定系数

# 先建立多元线性回归模型
> fm = lm(y~x1+x2+x3+x4,data = X)

# 计算多元线性回归模型决定系数
> R2 = summary(fm)$r.sq
> R2
[1] 0.9997162

# 计算复相关系数
> R = sqrt(R2)
> R
[1] 0.9998581

多变量相关分析能为回归分析服务

可以看出多变量相关分析跟回归分析的关系很密切，多变量相关分析能为回归分析服务，因为要具有相关性才有做线性回归拟合的价值。

具有相关性才有做线性回归拟合的价值

5、Python代码

参考：https://www.cnblogs.com/shengyang17/p/9649819.html

5.1.图示初判

（1）变量之间的线性相关性

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
% matplotlib inline

# 图示初判
# （1）变量之间的线性相关性

data1 = pd.Series(np.random.rand(50)*100).sort_values()
data2 = pd.Series(np.random.rand(50)*50).sort_values()
data3 = pd.Series(np.random.rand(50)*500).sort_values(ascending = False)
# 创建三个数据：data1为0-100的随机数并从小到大排列，data2为0-50的随机数并从小到大排列，data3为0-500的随机数并从大到小排列，

fig = plt.figure(figsize = (10,4))
ax1 = fig.add_subplot(1,2,1)
ax1.scatter(data1, data2)
plt.grid()
# 正线性相关

ax2 = fig.add_subplot(1,2,2)
ax2.scatter(data1, data3)
plt.grid()
# 负线性相关

（2）散点图矩阵初判多变量间关系

# 图示初判
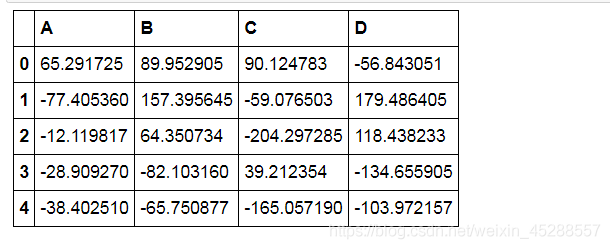
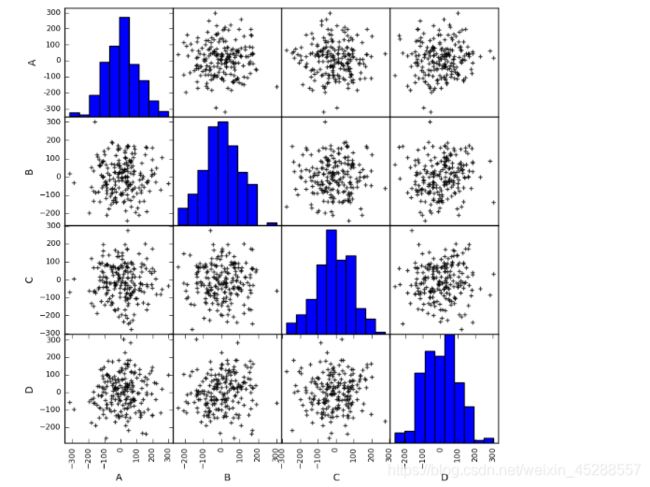
# （2）散点图矩阵初判多变量间关系

data = pd.DataFrame(np.random.randn(200,4)*100, columns = ['A','B','C','D'])
pd.scatter_matrix(data,figsize=(8,8),
                  c = 'k',
                 marker = '+',
                 diagonal='hist',
                 alpha = 0.8,
                 range_padding=0.1)
data.head()

5.2.Pearson相关系数（皮尔逊相关系数）

建立在正态分布之上的

分子是第一个变量X - 它的均值，第二个变量Y - 它的均值的求和，分母是两个平方根的积

# Pearson相关系数  

data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({'value1':data1.values,
                     'value2':data2.values})
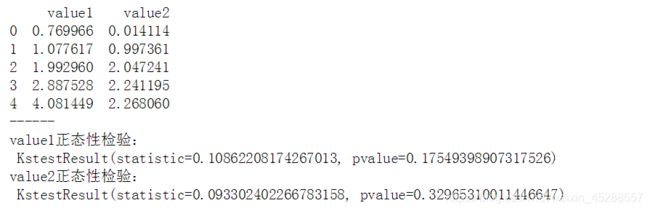
print(data.head())
print('------')
# 创建样本数据

u1,u2 = data['value1'].mean(),data['value2'].mean()  # 计算均值
std1,std2 = data['value1'].std(),data['value2'].std()  # 计算标准差
print('value1正态性检验：\n',stats.kstest(data['value1'], 'norm', (u1, std1)))
print('value2正态性检验：\n',stats.kstest(data['value2'], 'norm', (u2, std2)))
print('------')
# 正态性检验 → pvalue >0.05

data['(x-u1)*(y-u2)'] = (data['value1'] - u1) * (data['value2'] - u2)
data['(x-u1)**2'] = (data['value1'] - u1)**2
data['(y-u2)**2'] = (data['value2'] - u2)**2
print(data.head())
print('------')
# 制作Pearson相关系数求值表  

r = data['(x-u1)*(y-u2)'].sum() / (np.sqrt( data['(x-u1)**2'].sum() * data['(y-u2)**2'].sum() ))
print('Pearson相关系数为：%.4f' % r)
# 求出r
# |r| > 0.8 → 高度线性相关

# Pearson相关系数 - 算法   

data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({'value1':data1.values,
                     'value2':data2.values})
print(data.head())
print('------')
# 创建样本数据

data.corr() 
# pandas相关性方法：data.corr(method='pearson', min_periods=1) → 直接给出数据字段的相关系数矩阵
# method默认pearson

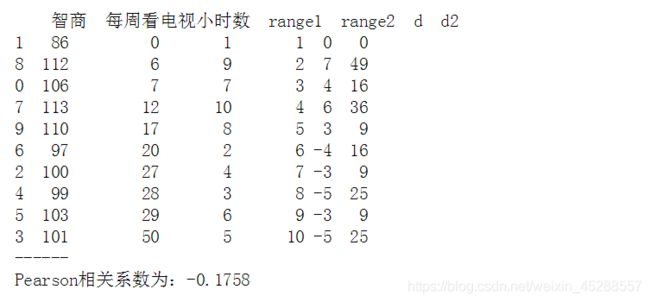
5.3.Sperman秩相关系数（斯皮尔曼相关系数）

# Sperman秩相关系数

data = pd.DataFrame({'智商':[106,86,100,101,99,103,97,113,112,110],
                    '每周看电视小时数':[7,0,27,50,28,29,20,12,6,17]})
print(data)
print('------')
# 创建样本数据

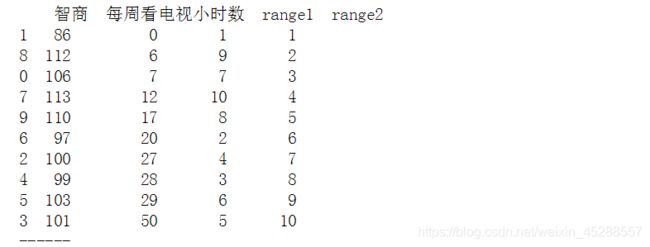
data.sort_values('智商', inplace=True)
data['range1'] = np.arange(1,len(data)+1)
data.sort_values('每周看电视小时数', inplace=True)
data['range2'] = np.arange(1,len(data)+1)
print(data)
print('------')
# “智商”、“每周看电视小时数”重新按照从小到大排序，并设定秩次index

data['d'] = data['range1'] - data['range2']
data['d2'] = data['d']**2 
print(data)
print('------')
# 求出di，di2
n = len(data)
rs = 1 - 6 * (data['d2'].sum()) / (n * (n**2 - 1))
print('Pearson相关系数为：%.4f' % rs)
# 求出rs

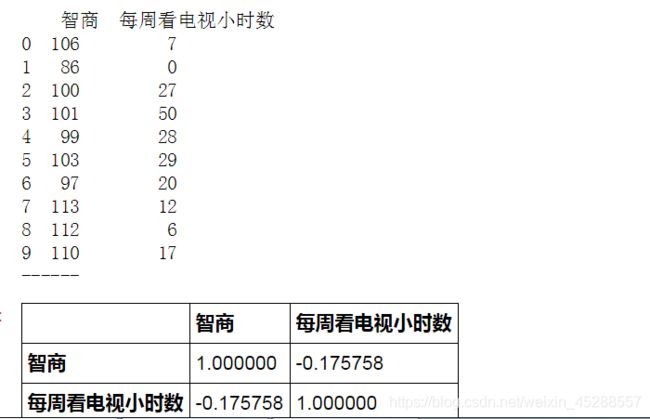
Pearson相关系数 - 算法

# Pearson相关系数 - 算法

data = pd.DataFrame({'智商':[106,86,100,101,99,103,97,113,112,110],
                    '每周看电视小时数':[7,0,27,50,28,29,20,12,6,17]})
print(data)
print('------')
# 创建样本数据

data.corr(method='spearman')
# pandas相关性方法：data.corr(method='pearson', min_periods=1) → 直接给出数据字段的相关系数矩阵
# method默认pearson