Scikit-Learn （从入门到放弃）一篇全解

目录

一、基础概念

 1、评估器（estimator）

2、实用函数

3、模型实例化

二、Scikit-Learn基础功能

1、数据集读取

2、数据集切分

3、标准化和归一化

（1）标准化（Standardization）

（2）归一化

三、sklearn中的逻辑回归评估器

使用逻辑回归评估器建模

四、sklearn中构建机器学习流

五、sklearn中保存模型

六、特征衍生，正则化（Regularization）

1、什么是正则化

2、经验风险与结构风险

3、特征衍生

4、加入正则项，降低结构风险，缓解过拟合

（1）岭回归（Ridge）

 （2）Lasso

 5、总结

 七、sklearn中的逻辑回归

相关概念​

官网连接：https://scikit-learn.org

一、基础概念

 1、评估器（estimator）

sklearn中的线性回归评估器LinearRegression是在sklearn包中的linear_model模块下

调用方法：

from sklearn.linear_model import LinearRegression

np.random.seed(9)   #设置随机数种子

features, labels = arrayGenReg(delta = 0.01)     #生成扰动值为0.01的数据
#调用模型需要进行实例化
model = LinearRegression()    #调用线性回归模型

X = features[:,:2]      #取前两列构造特征
y = labels      #构造标签

model.fit(X,y)      #调用模型进行训练

print(model.coef_)      #查看训练后的参数
print(model.intercept_) #查看训练后的截距

2、实用函数

调用sklearn中的MSE（方差）计算函数，用过程不需要进行实例化，直接导入相关模块即可。

#在metrics模块下导入MSE计算函数
from sklearn.metrics import mean_squared_error

mse=mean_squared_error(model.predict(X),y)
print(mse)

3、模型实例化

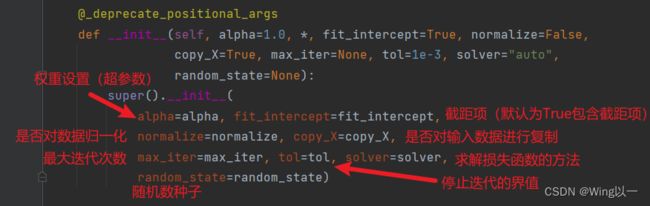
pycharm中右击评估器LinearRegression，如下图，进行查看：

 各项超参数的解释：

model.get_params()可以直接查看model的各项默认超参数取值。

model.get_params()可以修改已经实例化好的超参数。

 对于线性方程来说，模型训练后可查看如下属性：

 如果你想对线性回归了解更多，请看官网： 官网连接：https://scikit-learn.org/stable/

二、Scikit-Learn基础功能

1、数据集读取

Scikit-Learn提供内置数据集和创建数据集的方法，sklearn中的数据集相关功能都在datasets模块。下图为官网API截图：

 

 读取鸢尾花数据集：

from sklearn.datasets import load_iris

iris_data = load_iris()

#如果希望只返回特征矩阵和标签数组这两个对象，则可以通过在读取数据集时设置参数return_X_y为True来实现
X, y = load_iris(return_X_y=True)

2、数据集切分

train_test_split来进行数据集切分。`stratify`参数则是控制训练集和测试集不同类别样本所占比例的参数。令stratify=y，则测试集中0，1比例和训练集完全相同。

from sklearn.model_selection import train_test_split

#数据集切分
X = np.arange(16).reshape((8, 2))
y = np.array([0, 0, 0, 0, 1, 1, 1, 1])
#train_test_split(X, y, random_state = 24)     #random_state相当于一个随机数种子，设置不同切分结果不同，默认情况按照0.75：0.25切分
print(train_test_split(X, y, stratify=y, random_state=24))

3、标准化和归一化

（1）标准化（Standardization）

Z-Score标准化和0-1标准化，都属于Standardization。在sklearn中的Preprocessing data模块下。

Z-Score标准化函数调用：

from sklearn import preprocessing

X = np.arange(16).reshape((8, 2))
print(X)
print(preprocessing.scale(X))

Z-Score标准化评估器调用：

from sklearn.preprocessing import StandardScaler

#标准化(评估器调用）
scaler = StandardScaler()       #评估器实例化为对象
X = np.arange(16).reshape((8, 2))
X_train, X_test = train_test_split(X)

scaler.fit(X_train)

print(scaler.scale_)        #标准化后每一列的标准差
print(scaler.mean_)        #标准化后每一列的均值
print(scaler.var_)          #标准化后每一列的方差
print(scaler.n_samples_seen_)       #类似于稀疏矩阵中

#利用训练集的均值和方差对训练集进行标准化处理
X_train_standar = scaler.transform(X_train)
#利用训练集的均值和方差对测试集进行标准化处理
X_test_standar = scaler.transform(X_test)

print(X_train_standar)
print(X_test_standar)

#合并fit和transform
result_X_train = scaler.fit_transform(X_train)

print(result_X_train)

 一个算法模型的评估器在训练完成后，我们使用predict来进行预测。而一个标准化的评估器是利用transform进行数据的数值转化。

0-1标准化函数调用：

函数preprocessing.minmax_scale不仅可以做0-1标准化，还可以进行任何给定范围的标准化。

from sklearn import preprocessing

X = np.arange(16).reshape((8, 2))
print(preprocessing.minmax_scale(X))

0-1标准化评估器调用：

from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler()
print(scaler.fit_transform(X))
print(scaler.data_max_)
print(scaler.data_min_)

 sklearn中还有i对稀疏矩阵的标准化（MaxAbsScaler）、针对存在异常值点特征矩阵的标准化（RobustScaler）、以及非线性变化的标准化（Non-linear transformation）。

（2）归一化

sklearn中的归一化特指将单个样本（一行数据）放缩为单位范数（1范数或者2范数为单位范数）的过程。常见于核方法或者衡量样本之间相似性的过程中。

范数的基本概念，假设向量$x = [x_1, x_2, ..., x_n]^T$，则向量x的1-范数的基本计算公式为：

向量x的2-范数计算公式为： 

归一化的函数调用：

# 1-范数归一化过程
l1_norm = preprocessing.normalize(X, norm='l1')
# 2-范数归一化过程
l2_norm = preprocessing.normalize(X, norm='l2')
print(l1_norm )
print(l2_norm )

归一化的评估器调用：

from sklearn.preprocessing import Normalizer

normlize = Normalizer(norm = 'l1')
normlize.fit_transform(X)

三、sklearn中的逻辑回归评估器

1、使用逻辑回归评估器建模

from sklearn.linear_model import LogisticRegression

#数据准备
iris_data = load_iris()
X, y = load_iris(return_X_y=True)
#实例化模型
iris_Logis = LogisticRegression(max_iter=1000)
#代入全部数据进行训练（此处未进行数据集切分）
iris_Logis.fit(X,y)
#查看线性方程的系数
print(iris_Logis.coef_)
#在全部数据集上进行预测
iris_predict = iris_Logis.predict(X)[:10]       #做输出显示的话加[:10] 只预测前10个看一下
#查看概率判别结果
iris_proba= iris_Logis.predict_proba(X)[:10]
#查看分类模型准确率
iris_acc = iris_Logis.score(X,y)

from sklearn.metrics import  accuracy_score
#准确率计算的函数
iris_acc = accuracy_score(y, iris_Logis.predict(X))

四、sklearn中构建机器学习流

借助make_pipeline类的相关功能，将多个评估器类串联在一起，形成一个机器学习流。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import  accuracy_score
from sklearn.pipeline import make_pipeline
#可直接import sklearn


#实例化过程中输入要构建机器学习流的评估器
pipe = make_pipeline(StandardScaler(),LogisticRegression(max_iter=1000))           #将标准化和逻辑回归构建为一个机器学习流
#数据准备
iris_data = load_iris()
X, y = load_iris(return_X_y=True)
#数据集切分
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=24)
#训练模型
pipe.fit(X_train,y_train)
#在测试集上预测
iris_predict= pipe.predict(X_test)
#查看准确率
iris_acc = pipe.score(X_test,y_test)

五、sklearn中保存模型

使用joblib包里的dump函数来保存模型，用load函数来读取模型。

import joblib

#保存模型
joblib.dump(pipe,'pipe.model')      #如果要指定路径用路径+文件名‘D:/model/pipe.model’，第二个参数可以是str, pathlib.Path, or file object.
#读取模型
pipe_read = joblib.load('pipe.model')
#在训练集上预测
iris_predict2 = pipe_read.score(X_train, y_train)

六、特征衍生，正则化（Regularization）

1、什么是正则化

机器学习中正则化（regularization）的外在形式就是在模型的损失函数中加上一个正则化项（regularizer），有时也被称为惩罚项（penalty term），如下方程所示，其中L为损失函数，J为正则化项。通常来说，正则化项往往是关于模型参数的1-范数或者2-范数，也有可能是这两者的某种结合。

为何需要正则化：正则化核心的作用是缓解模型过拟合倾向；在某些时候，加入了正则化项之后会让损失函数的求解变得更加高效。

2、经验风险与结构风险

经验风险：给定一组参数后计算得出的损失函数的损失值。

结构造风险：可等价为模型复杂程度，模型越复杂，模型结构风险就越大。
正则化后的损失函数来求解最小值的同时，要求正则化项和其本身都能有较小的值，即可达到一个模型的经验风险和结构风险同时可控。

我们构造一个0到1之间等距分布24个点组成的ndarray，，其中r是人为制造的随机噪声。然后我们借助numpy的polyfit函数来进行多项式拟合，polyfit函数会根据设置的多项式阶数，在给定数据的基础上利用最小二乘法进行拟合，并返回拟合后各阶系数。

import numpy as np
import pandas as pd
import math
import sklearn

import matplotlib as mpl
import matplotlib.pyplot as plt

np.random.seed(24)

n_dots = 24
x = np.linspace(0,1,n_dots)     #从0到1等距排布的20个数
y = np.sqrt(x) + 0.3*np.random.rand(n_dots) - 0.2

def plot_polynomial_fit(x,y,deg):
    p = np.poly1d(np.polyfit(x,y,deg))
    t = np.linspace(0,1,100)
    plt.plot(x, y, 'ro',t, p(t),'-', t,np.sqrt(t), 'r--')

plt.figure(figsize=(24,4),dpi = 200)
title = ['Under Fitting','','Fitting','Over fitting']
for index, deg in enumerate([1,2,3,10]):
    plt.subplot(1, 4, index+1)
    plot_polynomial_fit(x, y, deg)
    plt.title(title[index], fontsize=18)
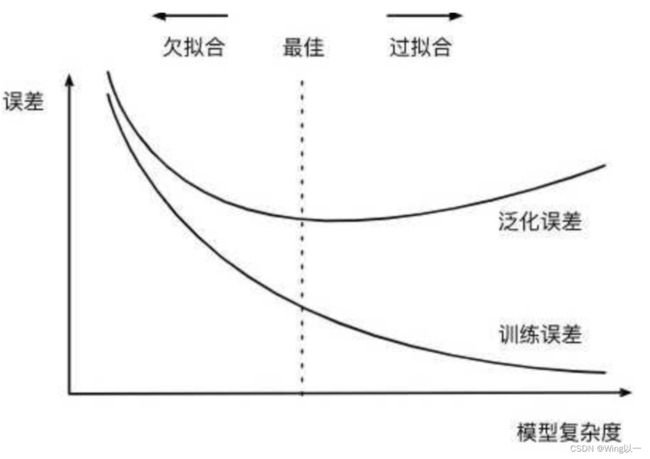
plt.show()

分别用一阶线性方程，二阶、三阶和十阶多项式来拟合我们的数据。结果如下： 

 对比发现在10阶多项式来拟合的时候，因拟合函数过于复杂导致结构风险过高。后续在大的数据集上不能很好的泛化。也就是过拟合，导致训练集上结果较好，而在测试泛化使用时偏差较大。

3、特征衍生

在原始数据中衍生出几个特征，分别是，然后带入线性回归方程进行建模。

手动特征衍生的方法如下：

x_l = []

for i in range (10):
    x_temp = np.power(x,i+1).reshape(-1, 1)
    x_l.append(x_temp)
X = np.concatenate(x_l, 1)

这种特征衍生的方法也可以通过sklearn中的PolynomialFeatures类来实现。

其参数解释如下：

# 二阶特征衍生
PolynomialFeatures(degree=2).fit_transform(x.reshape(-1, 1))[:2]

特征衍生后的新数据来进行线性回归建模

#特征衍生后的新数据来进行线性回归建模
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

lr = LinearRegression()
lr.fit(X, y)

print(lr.coef_)
print(mean_squared_error(lr.predict(X), y))

本来只有一个特征X时，我们进行线性回归的结构应该是一条直线（存在欠拟合的情况）。我们进行了10阶特征衍生后的结构如图（变得过拟合了）。

# 观察建模结果
t = np.linspace(0, 1, 200)
plt.subplot(121)
plot_polynomial_fit(x, y, 1)
plt.title('1-degree')
plt.subplot(122)
plt.plot(x, y, 'ro', x, lr.predict(X), '-', t, np.sqrt(t), 'r--')
plt.title('10-degree')

4、加入正则项，降低结构风险，缓解过拟合

在线性回归的损失函数中引入正则化，来缓解10阶特征衍生后的过拟合问题。

在线性回归中加入l2正则化，实际上就是岭回归（Ridge），而加入l1正则化，则变成了Lasso。

因此，围绕上述模型尝试进行岭回归和Lasso的建模。

（1）岭回归（Ridge）

scikit-learn: machine learning in Python — scikit-learn 0.16.1 documentation

 参数介绍：

from sklearn.linear_model import Ridge,Lasso

#参数较多，模型较简单的情况下，一个小的alpha也会对其产生较大的影响
reg_rid = Ridge(alpha=0.005)
reg_rid.fit(X,y)
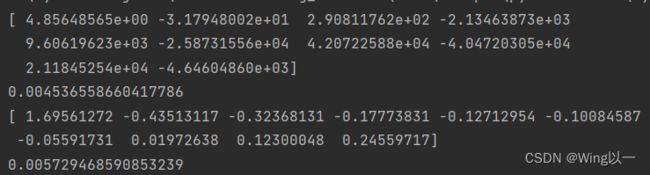
print(reg_rid.coef_)
print(mean_squared_error(reg_rid.predict(X), y))

观察岭回归对于过拟合的缓解情况：

岭回归其实是对所有取值缩小来降低l2范数的值。 

 （2）Lasso

reg_las = Lasso(alpha=0.001)

reg_las.fit(X, y)
print(reg_las.coef_)
print(mean_squared_error(reg_las.predict(X), y))

Lasso是将不重要的特征系数清零，保留更重要的特征系数。

 5、总结

综合以上内容，可以总结一些建模的策略：

• 当模型效果（往往是线性模型）不佳时，可以考虑通过特征衍生的方式来进行数据的“增强”；
• 如果出现过拟合趋势，则首先可以考虑进行不重要特征的筛选，过多的无关特征其实也会影响模型对于全局规律的判断，当然此时可以考虑使用l1正则化配合线性方程进行特征重要性筛选，剔除不重要的特征，保留重要特征；
• 对于过拟合趋势的抑制，仅仅踢出不重要特征还是不够的，对于线性方程类的模型来说，l2正则化则是缓解过拟合非常好的方法，配合特征筛选，能够快速的缓解模型过拟合倾向；

典型的可以通过正则化来进行过拟合倾向修正的模型主要有线性回归、逻辑回归、LDA、SVM以及一些PCA衍生算法（如SparsePCA）。而树模型则不用通过正则化来进行过拟合修正。

 七、sklearn中的逻辑回归

相关概念

 参数解释：

关于损失函数求解方法的选取，官网有如下表格： 

逻辑回归可选的优化方法包括：        

• liblinear，这是一种坐标轴下降法，并且该软件包中大多数算法都有C++编写，运行速度很快，支持OVR+L1或OVR+L2；      
• lbfgs，全称是L-BFGS，牛顿法的一种改进算法（一种拟牛顿法），适用于小型数据集，并且支持MVM+L2、OVR+L2以及不带惩罚项的情况；      
• newton-cg，同样也是一种拟牛顿法，和lbfgs适用情况相同；      
• sag，随机平均梯度下降，随机梯度下降的改进版，类似动量法，会在下一轮随机梯度下降开始之前保留一些上一轮的梯度，从而为整个迭代过程增加惯性，除了不支持L1正则化的损失函数求解以外（包括弹性网正则化）其他所有损失函数的求解；      
• saga，sag的改进版，修改了梯度惯性的计算方法，使得其支持所有情况下逻辑回归的损失函数求解；

 大多数情况，我们会优先根据多分类问题的策略及惩项来选取优化算法，其次，如果有多个算法可选可参考如下：

• Penalize the intercept (bad)，如果要对截距项也进行惩罚，那只能选取liblinear；      
• Faster for large datasets，如果需要对海量数据进行快速处理，则可以选取sag和saga；      
• Robust to unscaled datasets，如果未对数据集进行标准化，但希望维持数据集的鲁棒性（迭代平稳高效），则可以考虑使用liblinear、lbfgs和newton-cg三种求解方法