数据量少又不平衡，机器学习该如何建模（含 Python 代码）

​

A photo by Author

在学术研究与教学中，很多算法都有一个基本假设，那就是数据分布是均匀的。当我们把这些算法直接应用于实际数据时，大多数情况下都无法取得理想的结果。数据量少、不平衡问题，虽然不是最难的，但绝对是最重要的问题之一。

在这篇文章中，我们将分析校园安置数据，以在数据中获取学生被安置的因素。由于数据非常小，而且有点不平衡，我们尝试做 EDA（Electronic Design Automation 电子设计自动化）和机器学习建模以获得更好的结果。

数据集包含百分比、分数、课程专业化、经验等。有两个输出列，即对于回归，我们可以将工资作为输出；对于分类，我们可以将状态作为输出。

让我们导入所有需要的库。

# Import Libraries​

import pandas as pd​

import matplotlib.pyplot as plt

import numpy as np

from sklearn.metrics import log_loss, confusion_matrix

import seaborn as sns​from sklearn.neighbors

import KNeighborsClassifier​from sklearn.metrics

import roc_curve, auc , precision_score , classification_report​

from sklearn.tree

import DecisionTreeClassifier​

import warningswarnings.filterwarnings('ignore')​

from sklearn.metrics

import confusion_matrix​

from sklearn.multiclass

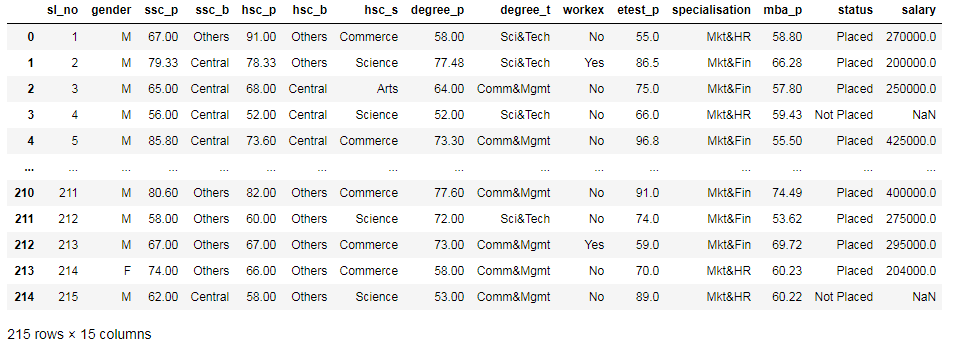
import OneVsRestClassifier

阅读并查看数据集。

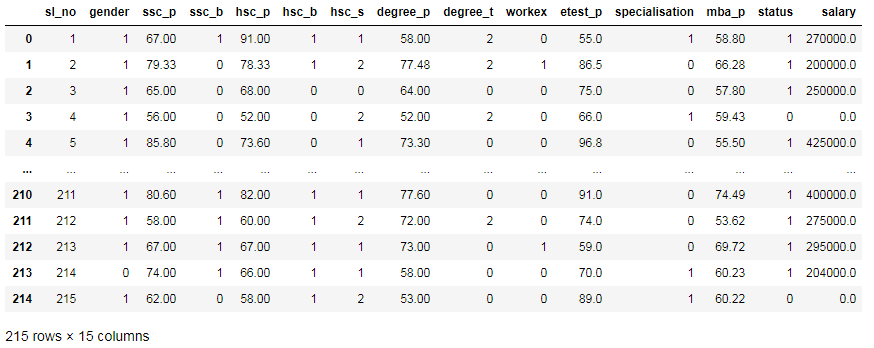
df = pd.read_csv('Placement_Data_Full_Class.csv')
df

A photo by Author

现在，我们将进行一些探索性数据分析。

df.info()

#output:



RangeIndex: 215 entries, 0 to 214

Data columns (total 15 columns):

# Column Non-Null Count Dtype

--- ------ -------------- -----

0 sl_no 215 non-null int64

1 gender 215 non-null object

2 ssc_p 215 non-null float64

3 ssc_b 215 non-null object

4 hsc_p 215 non-null float64

5 hsc_b 215 non-null object

6 hsc_s 215 non-null object

7 degree_p 215 non-null float64

8 degree_t 215 non-null object

9 workex 215 non-null object

10 etest_p 215 non-null float64

11 specialisation 215 non-null object

12 mba_p 215 non-null float64

13 status 215 non-null object

14 salary 148 non-null float64

dtypes: float64(6), int64(1), object(8)

memory usage: 25.3+ KB

映射群集的状态列

#replacing status column categories to 0 and 1

df['status'] = df['status'].map({"Placed":1, "Not Placed":0})​

#filling null values in salary with 0

df.salary.fillna(0,inplace=True)

​df.head()

A photo by Author

检查数据集中的缺失值

#missing values

df.isna().sum()

#output:

sl_no 0

gender 0

ssc_p 0

ssc_b 0

hsc_p 0

hsc_b 0

hsc_s 0

degree_p 0

degree_t 0

workex 0

etest_p 0

specialisation 0

mba_p 0

status 0

salary 0

dtype: int64

检查状态列以进行分类

sns.countplot(x="status", palette="dark", data=df);

A photo by Author

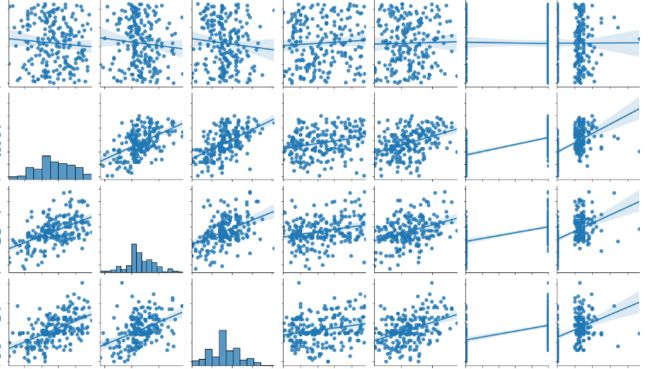
用 seaborn 库的 矩阵图（pairplot）对数据进行可视化检查

sns.pairplot(data=df, kind="reg");

A photo by Author

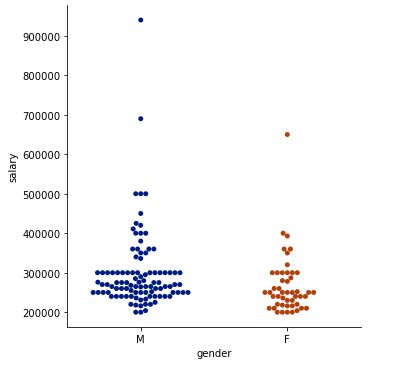
基于性别的工资核算

placed = df[df["status"]==1][["gender","salary", "workex"]]​

sns.catplot(y="salary", x="gender", kind="swarm", palette="dark" ,data=placed);

catplot. A photo by Author

似乎男性比女性的薪水更高。

数据预处理

需要对分类特征做标签编码

from sklearn.preprocessing

import LabelEncoderle=LabelEncoder()

for i in categorical:

df[i]=le.fit_transform(df[i])

df

A photo by Author

我们可以在上面的数据中看出，这些特征已被标记，并准备进入机器学习建模。

回归

df_reg_x = df.drop(['sl_no','salary'],1)

df_reg_y = df.salary

from sklearn.model_selection

import train_test_split

X_train, X_test, y_train, y_test = train_test_split(df_reg_x, df_reg_y, test_size = 0.15)

from sklearn.preprocessing

import StandardScalersc = StandardScaler()

X_train = sc.fit_trans

form(X_train)X_test = sc.trans

form(X_test)sc_y = StandardScaler()

y_train = sc_y.fit_trans

form(np.array(y_train).reshape(-1,1))

y_test = sc_y.trans

form(np.array(y_test).reshape(-1,1))

1. 线性回归（Linear Regression）

from sklearn.linear_model import LinearRegression

model1 = LinearRegression()

model1.fit(X_train,y_train)

y_pred = model1.predict(X_test)

from sklearn.metrics

import mean_squared_error, r2_score

print('MSE of Linear Regressor Model--->' , mean_squared_error(y_test,y_pred))

print('r2_score of Linear Model--->' , r2_score(y_test,y_pred))

#output:

MSE of Linear Regressor Model---> 0.06942385507687932

r2_score of Linear Model---> 0.9073385898967523

2. K 近邻回归（KNeighbors Regressor）

from sklearn.neighbors

import KNeighborsRegressor

neigh = KNeighborsRegressor(n_neighbors=11)

neigh.fit(X_train, y_train)

y_pred = neigh.predict(X_test)

from sklearn.metrics import mean_squared_error, r2_score

print('MSE of KNeighbors Regressor Model--->' , mean_squared_error(y_test,y_pred))

print('r2_score of Linear Model--->' , r2_score(y_test,y_pred))

#output:

MSE of KNeighbors Regressor Model---> 0.29273900427438526

r2_score of Linear Model---> 0.6092753867061032

3. 决策树回归（DecisionTree Regressor）

from sklearn.tree import DecisionTreeRegressor

regressor = DecisionTreeRegressor()

regressor.fit(X_train, y_train)

y_pred = regressor.predict(X_test)

print('MSE of DecisionTree Regressor Model--->' ,                     mean_squared_error(y_test,y_pred))

print('r2_score of Linear Model--->' , r2_score(y_test,y_pred))

#output:

MSE of DecisionTree Regressor Model---> 0.13344250885495113

r2_score of Linear Model---> 0.8218916102466214

分类

df_class_x = df.drop(['salary','sl_no','status'],1)

df_class_y = df.status

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(df_class_x, df_class_y, stratify=df_class_y, test_size = 0.15)

逻辑回归（Logistic Regression）

​

from sklearn.linear_model import LogisticRegression

from sklearn.metrics import roc_auc_score

from sklearn.model_selection import GridSearchCV

parameters = [{'C': [10**x for x in range(-4,5)]}]

K =[10**x for x in range(-4,5)]

K = np.log10(K)​

log= LogisticRegression(penalty='l2')

clf = GridSearchCV(log, parameters, cv=5, scoring='roc_auc',return_train_score=True)

clf.fit(X_train, y_train)​

train_auc= clf.cv_results_['mean_train_score']

train_auc_std= clf.cv_results_['std_train_score']

cv_auc = clf.cv_results_['mean_test_score']

cv_auc_std= clf.cv_results_['std_test_score']

lamb= clf.best_params_lamb = list(lamb.values())[0]

plt.figure(figsize=(10, 7))​

plt.plot(K, train_auc, label='Train AUC')

​plt.gca().fill_between(K,train_auc - train_auc_std,train_auc + train_auc_std,alpha=0.2,color='darkblue')​

plt.plot(K, cv_auc, label='CV AUC')​

plt.gca().fill_between(K,cv_auc - cv_auc_std,cv_auc + cv_auc_std,alpha=0.2,color='darkorange')

plt.scatter(K, train_auc, label='Train AUC points')

plt.scatter(K, cv_auc, label='CV AUC points')

plt.grid(True)

plt.legend()

plt.xlabel("C: hyperparameter")

plt.ylabel("AUC")

plt.title("ERROR PLOTS")

plt.show()

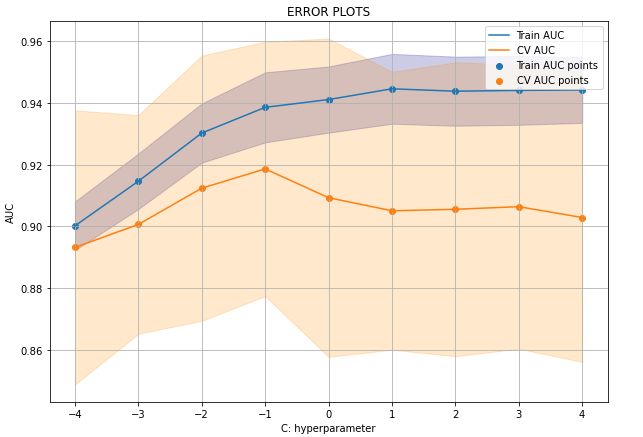
print('The best value of C is : ' , lamb)

Train and test AUR curve. A photo by Author

C 的最佳值为: 0.1

最佳超参数拟合模型（Fitting model）

log= LogisticRegression(penalty='l2',C = 0.001)

log.fit(X_train,y_train)

train_fpr, train_tpr, thresholds = roc_curve(y_train, log.predict_proba(X_train)[:,1])

test_fpr, test_tpr, thresholds = roc_curve(y_test, log.predict_proba(X_test)[:,1])

plt.plot(train_fpr, train_tpr, label="train AUC ="+str(auc(train_fpr, train_tpr)))

plt.plot(test_fpr, test_tpr, label="test AUC ="+str(auc(test_fpr, test_tpr)))

plt.legend()

plt.grid(True)

plt.xlabel("False Positive Rate")

plt.ylabel("True Positive Rate")

plt.title("ROC Curve")

plt.plot([0, 1], [0, 1],'r--')

plt.xlim([0, 1])

plt.ylim([0, 1])

plt.show()

​

ROC curve. A photo by Author

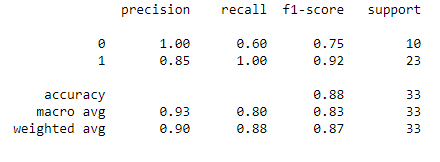
列印分类报告

y_pred = log.predict(X_test)
print (classification_report(y_test,y_pred))

A photo by Author

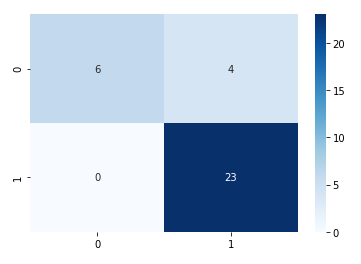
混淆矩阵（Confusion Matrix）

heatmap(confusion_matrix(y_test,y_pred), annot=True,fmt="d",cmap='Blues')

A photo by Author

结语：面对数据少且不平衡时，我们对其进行校正后，可以应用回归和分类算法。

---

作者：Amit Chauhan

出处：https://pub.towardsai.net/machine-learning-modeling-data-with-python-92bfebfe4052

改写：学姐