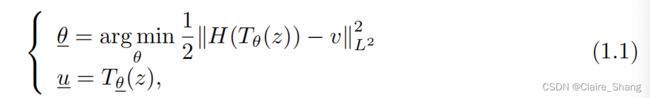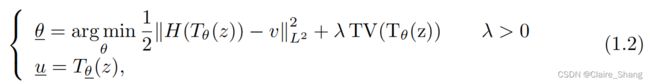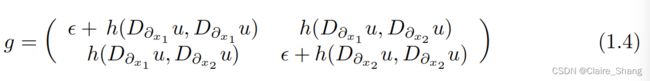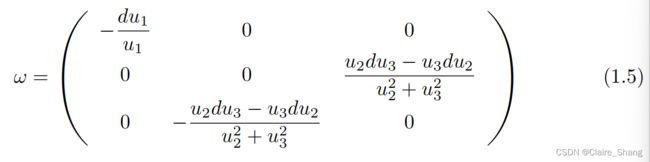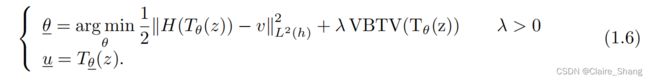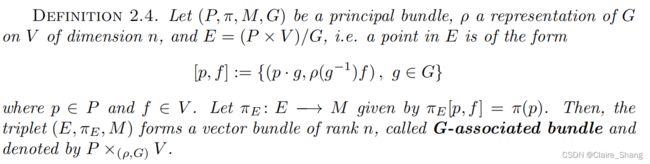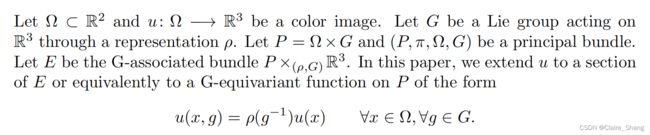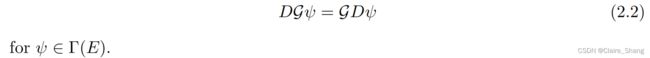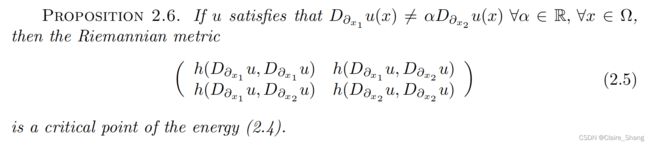DIP-VBTV: Color Image Restoration Model Combining Deep Image Prior and Vector Bundle Total Variation

目录

0 Abstract.

1、Introduction.

1.1. New perspective on image restoration / 图像恢复的新视角

1.2. Related work.

1.2.1. VBTV priors to express perceptual invariance / VBTV先验表示感知不变性

1.2.2. Deep Image Prior.

1.3. Contribution. 我们在本文中的贡献有三个方面

1.3.1. Construction of an optimal geometric triplet / 最优几何三元组的构造

1.3.2. Perceptual invariance associated to the minimization of VBTV induced by well-chosen geometric triplets. / 感知不变性与精心选择的几何三元组诱导的VBTV最小化相关

1.3.3. A variational model for color image restoration combining DIP and VBTV priors / 一种结合DIP和VBTV先验的彩色图像恢复的变分模型

2. 彩色图像恢复的几何三联体构造

2.1 G-相关束上几何三重态的概念和引入的向量束全变分

2.1.1. 彩色图像作为G-相关束的一部分

 2.1.2. G相关束上的几何三元组

 2.1.3. 几何三元组诱导的协变导数和向量束全变分(VBTV)

2.2. 推广结构张量的一个最优黎曼度量

2.3. 在一个R+* × SO(2)相关束上的一个最佳连接1形式及其在彩色成像中的解释

2.3.1.最优连接1型和相应的协变导数的平行截面

3. DIP-VBTV for image restoration

3.1. 关于求解优化问题的数值格式

3.1.1. A boosting numerical scheme.

3.1.2. Stopping criteria.

3.1.3.模型的参数和数值格式

 3.2. DIP-VBTV for denoising. ​编辑​编辑

3.3. DIP-VBTV model for deblurring.  ​编辑

 4. Conclusion.

---

录

• 前言
• 一、pandas是什么？
• 二、使用步骤
  • 1.引入库
  • 2.读入数据
• 总结

---

0 Abstract.

在本文中，我们引入了一种新的彩色图像恢复的变分模型，称为DIP-VBTV，它结合了两种先验：深度图像先验(DIP)，它假设恢复后的图像可以通过神经网络生成，以及一个向量束全变分(Vector Bundle Total Variation，VBTV)，它推广了向量束上的向量向量全变分(VTV)。VBTV由一个几何三元组决定：一个基流形上的黎曼度量，一个协变导数和一个向量束上的度量。VTV先验促使恢复后的图像是分段常数，而VBTV先验促使它们相对于协变导数是分段平行的。对于精心选择的几何三元组，我们证明了VBTV的最小化促使恢复模型的解决方案与干净的图像共享一些视觉内容。然后，我们在实验中表明，DIP-VBTV通过超越DIP-VTV和最先进的无监督方法而受益于这一特性。它证明了结合DIP和VBTV 先验的实用性.

1、Introduction.

1.1. New perspective on image restoration / 图像恢复的新视角

      人们对在图像处理和计算机视觉中设计受人类视觉启发的数学模型越来越感兴趣。处理自然图像的恢复，这种方法是合理的，因为其目的是保持对原始场景的感知，而不是再现其光强度。这是一项具有挑战性的任务，因为在恢复模型中包含的人类视觉系统(HVS)的属性依赖于在输入图像上观察到的退化，而且很可能描述HVS的期望属性的视觉模型必须进行调整，以适应图像处理模型。

    观察到一个干净的图像和它的退化版本(有噪声、模糊、下采样，…)仍然共享一些视觉内容，我们声称图像恢复模型应该考虑到这些信息。这可以通过使模型保留，或最多稍微修改退化图像的一些视觉属性来实现。尽管如此，应该保留的特征取决于退化的性质。例如，在处理噪声时，原始干净图像的颜色被广泛改变（例如，色调被修改），而局部结构（边缘，纹理）仍然可见也不是太高（在现实情况下也是这样）。另一方面，当退化来自于模糊算子时，局部结构比颜色退化更严重。因此，图像恢复模型一方面应该足够通用，编码局部结构和颜色感知的一些不变性，但也能够适应给定的退化算子的不变性。

1.2. Related work.

1.2.1. VBTV priors to express perceptual invariance / VBTV先验表示感知不变性

    在过去的30年里，变分模型已经证明了它们在处理图像恢复方面的效率，如去噪、去模糊、修补、超分辨率等。它们通常表示为一个数据项和一个或多个惩罚项的凸组合，后者由一些图像先验决定。

    在许多图像去噪的方法中，局部结构的感知在(真实的)噪声退化下几乎是不变的，这一事实被隐式编码为惩罚项。在编码这种不变性的重要惩罚项中，我们有全变分(TV)，它们的最小化鼓励通过欧氏梯度的L1范数来保存局部结构。第二个例子是Polyakov作用[26]，它的最小化鼓励通过黎曼梯度的L2范数来保持局部结构，黎曼度量与图像的结构张量有关。这两个惩罚项可以直接推广到彩色图像，用向量值函数的雅可比矩阵代替标量函数的梯度。例如，TV延伸到向量全变分(VTV)。

  TV的一个更基于感知的颜色扩展是饱和值全变分(Saturation-Value Total Variation，SVTV)[20]，该算法考虑了自然图像局部结构的空间变异主要表现在消色差分量上。然后, SVTV惩罚平滑的消色差分量的图像，从而其局部结构。这使得SVTV在彩色图像去噪方面优于VTV。

    在[2]中，提出了一种新的成像几何设置，即将彩色图像视为向量束的一部分。 在这种情况下，向量束总变异(VBTV)作为VTV的自然延伸而出现， 定义为对于u可微段，  VBTV(u) = ||Du||L1(g -1⊗h)。其中g为基流形上的黎曼度l量，D为由连接1型ω确定的协变导数，h为向量束上的定的正度量(VBTV(u)的显式表达式见2.1.3节)，因此，VBTV由几何三重态g, h， ω决定。然后，作者考虑了一个特殊的几何三重态，它编码了噪声退化下局部结构的一些不变性。实验表明，该VBTV比标准VTV具有更好的先验去噪效果，可以提供更好的恢复图像(较高的PSNR和SSIM)。最近，这种方法与SVTV结合，产生了一种局部结构主要在消色差分量的VBTV编码，并提供了更好的结果[29]。

    除去噪外，这些先验/惩罚项也被应用于各种图像恢复问题，如去模糊、修复、超分辨率[14]等.虽然它们确实编码了一些关于噪声退化的感知不变性，但它们并没有编码任何关于其他退化的感知不变性。然后，我们声称一个图像恢复模型将受益于考虑基于退化的惩罚项。

1.2.2. Deep Image Prior.

  在上述图像恢复的变分模型中，最小化是在具有有界变分的函数或截面空间上进行的。最近，一种新的图像恢复先验被引入，称为深度图像先验(DIP)[27]。在这个框架中，最小化是在一个精心选择的神经网络生成的一组函数上执行的。更准确地说，引入了以下最小化问题

 其中Tθ是由θ参数化的神经网络，其输入z是随机多通道图像，v是观察到的退化图像，H是退化算子，u是恢复图像。实验表明，模型（1.1）在去噪和超分辨率上在很大程度上优于基于VTV的标准恢复模型。

  最近，DIP被结合到[22]中的一个（各向异性）TV中，产生了所谓的“DIP-TV模型”

 实验表明，DIP- TV在去噪和去模糊方面优于DIP.

1.3. Contribution. 我们在本文中的贡献有三个方面

1.3.1. Construction of an optimal geometric triplet / 最优几何三元组的构造

     给定一个彩色图像u = (u1, u2, u3): Ω⊂R2−→R3被视为向量束的一部分，我们考虑可微能量

 并在第2节中确定一些临界点。

  最优黎曼度量。固定ω和h，我们证明，对于ɛ>0小，黎曼度量g

 在Ω上的笛卡尔坐标系(x1，x2)诱导的坐标系(∂x1，∂x2)中，近似于能量的一个临界点（1.3）。

  最佳连接1-form. 固定g和h，并假设ω是R×so（2）⇒值，我们证明了能量（1.3）具有一个唯一的临界点，由

 关于最优向量束度量的存在性。确定g和ω，我们表明能量(1.3)不具有临界点。

1.3.2. Perceptual invariance associated to the minimization of VBTV induced by well-chosen geometric triplets. / 感知不变性与精心选择的几何三元组诱导的VBTV最小化相关

    一个向量束度量可以用来为不同的图像分量分配不同的权重。然后，通过VBTV的最小化，矢量束度量可以在比其他图像组件更小的范围内处理一些图像组件。在图像去噪的环境中，这可能是一个理想的属性。事实上，通过将有噪声的图像的消色差分量平滑到比其彩色分量更小的程度，VBTV的最小化使得恢复后的图像的局部结构与退化后的图像相似，从而与干净图像相似。这正是上述SVTV先验的目的。

     VBTV的最小化鼓励生成相对于相应的协变导数分段平行的图像。在第2.3.1节中，我们表明，在假设u是一个在精心选择的消色差空间(如对抗空间)中表达的模糊图像的前提下，由最优连接1-形式(1.5)诱导的协变导数的平行部分与u和干净的原始图像共享一些感知内容。因此，VBTV的最小化鼓励恢复后的图像与干净的图像共享一些感知内容。我们还证明了连接1-形式（1.5）的对偶，在第1节中定义。2.3.2，满足类似的性质。

     形式（1.4）的黎曼度量是对Beltrami框架[26]中使用的黎曼度量的向量束的推广。后者近似于图像的结构张量（尺度为0），已知它可以提供一些关于其局部结构的信息。我们在本文进行的实验中表明，图像恢复得益于黎曼度量(1.4)的使用。

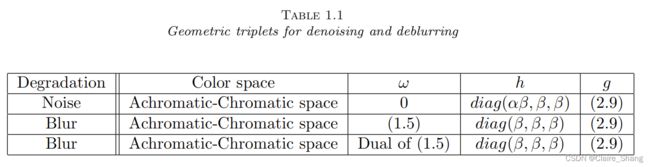
   基于此分析，我们考虑表1.1所描述的几何三联体，对于精心选择的β > 0,0 < α < 1。

1.3.3. A variational model for color image restoration combining DIP and VBTV priors / 一种结合DIP和VBTV先验的彩色图像恢复的变分模型

   为了证实我们的主张，即恢复模型应该考虑到干净的图像和退化的图像共享一些视觉内容，我们将VBTV作为图像恢复变分问题的一个惩罚项，从而得到DIP-VBTV模型

 它推广了DIP(1.1)和DIP- TV(1.2)。

     在第3.2节和第3.4节中，我们测试了DIP-VBTV对带有加性高斯白噪声的彩色图像的恢复。在3.3节和3.4节中，我们测试了DIP-VBTV对被高斯模糊破坏的彩色图像的恢复。

    代码：https://github.com/tombatard/dip_vbtv.

2. 彩色图像恢复的几何三联体构造

2.1 G-相关束上几何三重态的概念和引入的向量束全变分

2.1.1. 彩色图像作为G-相关束的一部分

   首先回顾G-相关束的节与主束上的G-等变函数之间的对应关系。

 相关束的截面与主束上的G等变函数之间存在对应关系。

 接下来，我们用TM表示M的正切束，用T * M表示M的余切束，由G(E)得到作用于G群中矩阵给出的E的纤维上的线性映射束。

 2.1.2. G相关束上的几何三元组

 流形M上g相关束上的几何三元组是一个三元组(g, h， ω)，其中：

• g是基流形上的黎曼度规: 流形上的黎曼度量是其切线束上的正定度量。
• h是束上的一个正定度量: 向量束E上的一个正定度量h是在每个光纤π-1E(x)上的一个正定标量积hx的赋值。
• ω是束上的1形连接: 连接1形式是Γ(T * M⊗g(E))集合中的一个元素，它在运动坐标系变化时满足一定的变换规律。更准确地说，设ω为运动坐标系中连接1形式的表达式，G为另一个运动坐标系。那么，ω在坐标系G中的表达式为

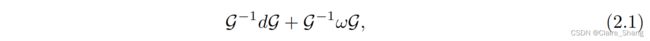
       其中d代表标准微分算子. 注意，根据公式(2.1)，连接1型完全由其在运动框架中的值决定。

 2.1.3. 几何三元组诱导的协变导数和向量束全变分(VBTV)

G相关束上的协变导数E为微分算子D:= d + ω，其中d为标准微分算子，ω为连接1形式.

变换定律(2.1)使D在运动坐标系变化时满足G等变性质，即

 在TM上的黎曼度量g和在E上的正定度量h决定了在T∗M⊗E上的正定度量g-1⊗h和在Γ上的Lp范数(T∗M⊗E)。特别是，我们有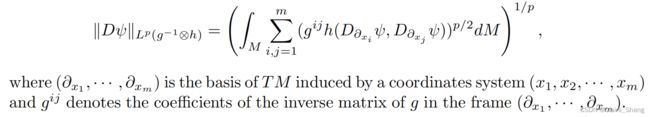

Definition 2.5. ψ∈Γ(E)的向量束全变分(VBTV)是这个量

 我们用BV(E)表示部分ψ的集合使 VBTV（ψ）<∞.   备注：与[2]不同，我们在VBTV的定义中不要求协变导数与向量束度量h兼容。

2.2. 推广结构张量的一个最优黎曼度量

设u是一个彩色图像，被视为G相关束的一段，该束具有连接1-form ω和一个确定的正向量束度量h。我们考虑以下能量  我们得到如下结果.

~ 命题2.6    如果u满足........，那么黎曼度量  (2.5) 是能量（2.4）的一个临界点.（文中有证明）

2.3. 在一个R+* × SO(2)相关束上的一个最佳连接1形式及其在彩色成像中的解释

2.3.1.最优连接1型和相应的协变导数的平行截面

设u是一个彩色图像，它是一个G相关束的一部分，该束具有黎曼度量g和一个正定向量束度量h。在不失一般性的情况下，我们假设u在一个移动的框架中表示，其中h是欧几里得度量||  ||2。我们考虑了能量 在本节中，我们假设李群表示(ρ， G)是通过下面表示  作用于R3上的R+∗× SO(2)

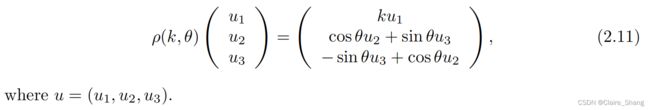能量的临界点(2.10)相对于群体表征(2.11)。我们得到如下结果。 

注意，为了强调它对u的依赖性，我们用ωu表示1-形式(2.12)。

由（2.12）诱导的协变导数的平行截面。设v为一节，而ωv为由v导出的最优连接1-形式（2.12）。我们有以下结果

 太长了太长了，实在是看不下去，我要跳过了！！！

3. DIP-VBTV for image restoration

在本节中，我们将使用表2.1中描述的用于去噪的几何三联体(g、h、ω)(H≡Id)和表2.2中描述的用于去模糊的几何三联体(g、h、ω)进行处理(H是一个模糊运算符) 测试模型DIP-VBTV 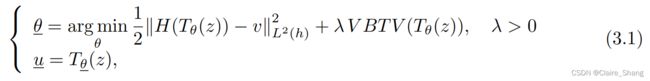本节所有实验均采用相同的Tθ网络。
它是一个编码器-解码器，具有上下两层之间的跳跃连接。它对应于[27]中的默认网络，关于体系结构的详细信息，我们将参考该网络。其中，对于大小为M × N × 3(3表示颜色通道数)的输入图像v，网络的输入z为大小为M × n × 32的随机图像.

3.1. 关于求解优化问题的数值格式

3.1.1. A boosting numerical scheme.

遵循[27]的方法，用E(θ;z)的能量在(3.1)中，我们考虑以下数值格式，以近似模型DIP-VBTV的解

3.1.2. Stopping criteria.

数值格式会出现不稳定的问题。这意味着在迭代过程中，能量E(θk；zk)会显著增加，从而在图像Tθk(zk)中产生模糊. 为了防止失稳，[27]采用的策略是跟踪优化损失，当连续两次检查点迭代的损失差值大于一定阈值时，从前一次检查点迭代返回参数。........在本文的实验中，我们遵循[27]中的策略。

3.1.3.模型的参数和数值格式

我们将这些参数分为两类：

1. 模型DIP-VBTV（3.1）的参数：
2. 数值格式(3.2)的参数:     -基于噪声的正则化的方差σ，学习率lr，指数滑动窗的权重γ，                                                -迭代次数，必须根据3.1.2节仔细选择。

 3.2. DIP-VBTV for denoising.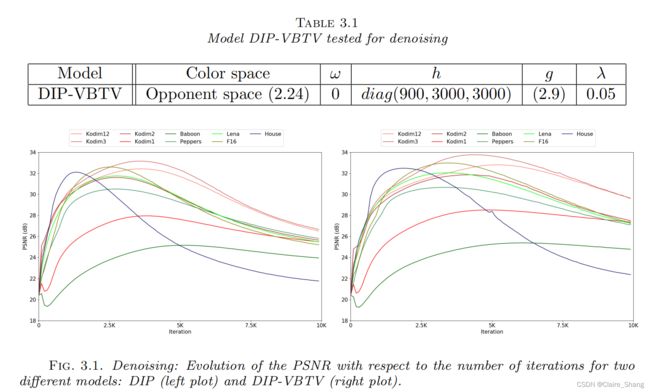

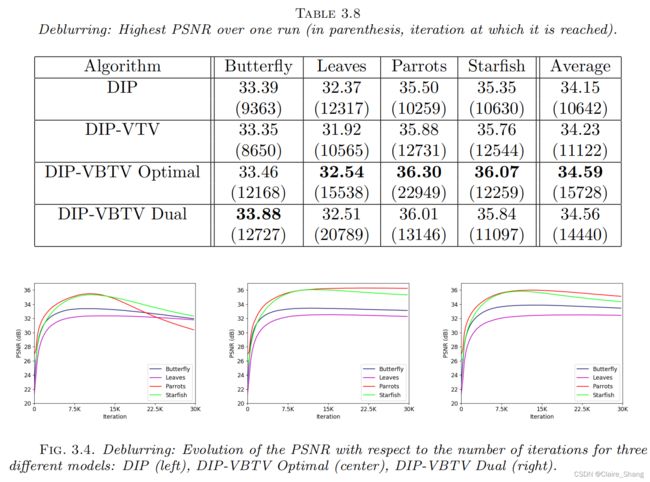
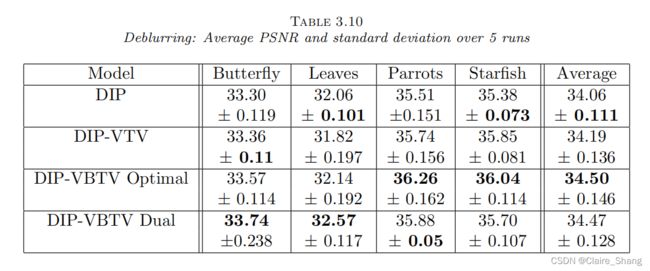
3.3. DIP-VBTV model for deblurring.  

还有好长好长，跳过跳过，决定看别的文章了。勉强把总结写上吧 

 4. Conclusion.

 本文提出了一种彩色图像复原的变分模型DIP-VBTV，该变分模型结合了由几何三元组确定的矢量束总变分(VBTV)和由神经网络确定的深度图像先验(DIP)两种先验。我们表明，对于作为能量临界点的精心选择的几何三联体，VBTV的最小化鼓励DIP-VBTV的解决方案与干净的图像共享一些视觉内容。然后，我们在实验中表明，修复受益于这种特性。事实上，我们用这些几何三元组对DIP- vbtv进行了去噪和去模糊测试，结果表明，它优于其他涉及DIP的方法。结果还表明，能提供最佳效果的几何三元组既依赖于图像本身，也依赖于退化算子。进一步的工作将致力于研究是否存在能提供更好的去噪和去模糊效果的几何三联体，并在其他图像恢复问题上测试DIP-VBTV。