基于朴素贝叶斯算法实现情感分类

互联网外卖以服务、快捷为卖点，用户的评论与反馈对商家、平台都很重要。本文根据数据中的评论，采用朴素贝叶斯算法来分析用户情感，将用户评论划分为“好评”，“差评”。训练数据集的准确率为99.44%，测试数据集的准确率为81.70%。

算法原理

贝叶斯定理

贝叶斯定理是一个计算条件概率的公式。通过已知概率计算未知的概率，比如我们记$A$的概率是$P(A)$，$B$的概率是$P(B)$，则$P(A|B)$表示观察到事件$B$发生时，事件$A$发生的概率，则其数学表达为：
$$P(A|B)=\frac{P(A)P(B|A)}{P(B)}$$
比如我们记$P(A)$为遇见四川人的概率，$P(B)$为遇见爱吃火锅的人的概率，那么$P(A|B)$就是遇见爱吃火锅的人时，他是四川人的概率。
其中，我们把$P(A)$称为先验概率，即我们在不知道$B$事件的前提下，对$A$事件概率的主观判断。在上面的例子中，就是在不知道他是不是喜欢吃火锅的人的前提下，来主观判断他是四川人的概率。
公式里的$P(B|A)/P(B)$称为“可能性函数”，这是一个调整因子，即新信息$B$带来的调整，作用是使得先验概率更接近真实概率。
$P(A|B)$称为“后验概率”，即在事件$B$发生之后，我们对$A$事件的概率的重新评估。在例子里是遇到爱吃火锅的人后，对他是四川人的概率的重新预测。

朴素贝叶斯分类法

朴素贝叶斯分类法是基于贝叶斯定理和特征条件独立假设的分类方法，它通过特征计算分类的概率，选取概率大的情况，是基于概率论的一种机器学习分类（监督学习）方法，被广泛应用于情感分类领域的分类器。
朴素贝叶斯算法可以用一句话来概括：贝叶斯定理+条件独立假设。条件独立假设指的是：在解决分类问题时，会选取很多数据特征，为了降低计算复杂度，假设数据各个维度的特征相互独立。

多项式分布

多项式分布是指满足类别分布的实验，连续做$n$次后，每种类别出现的特定次数组合的概率分布情况。假设，$x_i$表示类别$i$出现的次数，$p_i$表示类别$i$在单次实验中出现的概率。当满足前提条件${\sum }_{i=1}^k{x}_i=n$时，由随机变量$x_i$构成的随机向量$X=[x_1,\cdots ,x_k]$ 满足以下分布函数：
$$f(X,n,P)=\frac{n!}{{\prod }_{i=1}^k{x}_i!}\prod _{i=1}^k{p}_i^{x_i}$$
其中，$P$是由各个类别的概率构成的向量，即$P=[P_1,\cdots ,P_k]$，$k$表示类别的总数，$n$表示实验进行的总次数。也可以把${\prod }_{i=1}^k{p}_i^{x_i}$理解为按照特定顺序，所有类别出现的某个特征的次数组合的概率。二项式分布和多项式分布结合朴素贝叶斯算法，经常被用来实现文章分类算法。例如，有一个论坛需要对用户的评论进行过滤，屏蔽掉不文明的评论。首先需要有一个经过标记的数据集，我们称为语料库。假设使用人工标记的方法对评论进行人工标记，标记为$1$表示包含不文明用语评论，标记为$0$表示正常评论。
假设我们的词库大小为$k$，则文章中出现的某个词可以看成是一次满足$k$个类别的类别分布实验。我们知道一篇评论是由$n$个词组成的，因此一篇文章可以看成是进行$n$次符合类别分布的实验后的产物。由此得知，一篇评论文章服从多项式分布，它是词库里的所有词语出现的次数组合构成的随机向量。一般情况下，词库比较大，评论文章只是由少量词组成，所以这个随机向量很稀疏，即大部分元素为$0$。通过分析语料库，我们容易统计出每个词出现不文明评论及正常评论文章里的概率，即$p_i$的值。
同时，针对待预测的评论文章，我们可以统计出词库里的所有词在这篇文章里的出现次数，即$x_i$的值及评论文章的词语个数$n$。代入多项式分布的概率质量函数：
$$f(X,n,P)=\frac{n!}{{\prod }_{i=1}^k{x}_i!}\prod _{i=1}^k{p}_i^{x_i}$$
我们可以求出，待预测的评论文章构成的随机向量$X$，其为不文明评论的相对概率。同理也可求出其为正常评论的相对概率，通过比较两个相对概率，就可以对这篇文章输出一个预测值。
同理，本文所采用的数据包含评论和标签，标记为$1$表示好评，标记为$0$表示差评。一篇评论由$n$个词组成，因此一条评论可以看成是进行$n$次符合类别分布的实验后的产物。由此得知，一条评论服从多项式分布，它是词库里的所有词语出现的次数组合构成的随机向量。通过分析语料库，我们容易统计出每个词出现在差评及好评评论里的概率，即$p_i$的值。

TF-DIF

TF-IDF是一种统计方法，用以评估一个词语对于一份文档的重要程度。TF表示词频，对一份文档而言，词频是特定词语在这篇文档里出现的次数除以文档的词语总数。
IDF表示一个词的逆向文档频率指数，可以由总文档数目除以包含该词语的文档数目，再将得到的商取对数得到，它表达的是词语的权重指数。
计算出每个词的词频和权重指数后，两者相乘，即可得到这个词在文档中的重要程度。

情感分类的实现

在scikit-learn里，朴素贝叶斯算法在{sklearn.native_bayes}包里实现，本文我们使用MultinomialNB来分析情感，实现评论的分类。

获取数据

数据来自和鲸社区，12k条外卖用户评价。
其中有$4000$好评，$7987$ 为差评。文件里共有$2$列数据，第$1$列label表示评论的标签，即标记为$1$表示好评，标记为$0$表示差评。第$2$列review内容为用户的评论。

data = pd.read_csv("D:/waimai_10k.csv")
review=data['review'].values
label=data['label'].values

我们将数据分成训练集和测试集，其中80%为训练集，20%为测试集。

from sklearn.model_selection import train_test_split
Xtrain, Xtest, Ytrain, Ytest = train_test_split(review, label, test_size=0.20, random_state=2);

t1=Xtrain.tolist()
t2=Ytrain.tolist()
news_train = {'review':t1, 'label': np.array(t2)}

查看一下数据的详细内容，例如第一条评论的文本信息，以及评论所属类别标签。

news_train["review"][0]
news_train["label"]

输出的结果为：
‘鸡翅不是奥尔良味道，排骨不新鲜，送餐慢，披萨还凑合’
array([0, 1, 1, …, 0, 1, 0])
可以看到，第一条评论对应的标签是“0”，也就是差评。

评论的数学表达

把训练用的语料库导入内存，其中news_train[‘review’]是一个数组，里面包含了所有评论的文本信息。

print("summary: {0} documents in 2 categories.".format(len(news_train['review'])))

输出结果为：
summary: 9589 documents in 2 categories.
可以看到，我们的语料库共有$9589$个评论，其中被分成$2$个类别。接下来我们把这些评论全部转换为由TF-IDF表达的权重信息构成的向量。

from sklearn.feature_extraction.text import TfidfVectorizer
t = time()
vectorizer = TfidfVectorizer(encoding='latin-1')
X_train = vectorizer.fit_transform((d for d in news_train["review"]))
print("n_samples: \%d, n_features: \%d" \% X_train.shape)

TfidfVectorizer类是用来把所有评论转化为矩阵，该矩阵每行都代表一条评论，一行中的每个元素代表一个对应的词语的重要性，词语的重要性由TF-IDF来表示。
输出结果为：
n_samples: 9589, n_features: 24992
由程序输出可以知道，我们的词典总共有$24992$个词语，即每条评论都可转换为一个$24992$维的向量。X_train是一个维度为$9589\times 249992$的稀疏矩阵。

模型训练

我们已经把评论数据转化为scikit-learn里典型的训练数据集矩阵：矩阵的每一行表示一个数据样本，矩阵的每一列表示一个特征。然后可以直接使用MultinomialNB对数据集进行训练。

from sklearn.naive_bayes import MultinomialNB
y_train = news_train["label"]
clf = MultinomialNB(alpha=0.0001)
clf.fit(X_train, y_train)
train_score = clf.score(X_train, y_train)
print("train score: {0}".format(train_score))

其中，$\alpha$表示平滑系数，其值越小，越容易造成过拟合，值太大，容易造成欠拟合。
输出结果如下：
train score: 0.9943685472937741
接着我们用测试集的一条评论来预测其是否准确。

t11=Xtest.tolist()
t22=Ytest.tolist()
news_test = {'review':t11, 'label': np.array(t22)}
print("summary: {0} documents in 2 categories.".format(len(news_test['review'])))

可以看到我们测试集的数据共有$2398$条评论。
接下来通过同样的操作对文档进行向量化。查看训练出来的模型能否正确地预测这个评论所属的类别。

pred = clf.predict(X_test[0])
print("predict: {0} is in category {1}".format(
news_test["label"][0], pred[0]))
print("actually: {0} is in category {1}".format(
    news_test["label"][0], [news_test["label"][0]][0]))

输出结果如下。
predict: 0 is in category 0
actually: 0 is in category 0
可以看到，预测结果与实际结果相符，预测准确。

模型评价

通过验证，我们的模型是可用的。接下来我们需要对模型有个全方位的评价。
首先对测试数据集进行预测。

pred = clf.predict(X_test)
test_score = clf.score(X_test, y_test)

输出结果为：
test score: 0.816930775646372
接着使用classification_report()函数来查看一下针对每个类别的预测准确性，在笔者计算机输出结果如下。

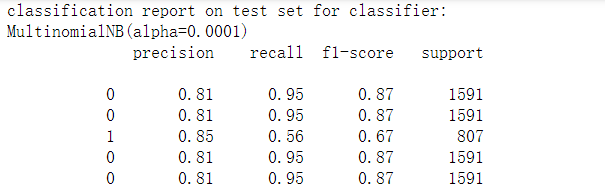
此外还可以通过confusion_matrix()函数生成混淆矩阵，观察每种类别被错误分类的情况。

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, pred)
print("confusion matrix:")
print(cm)

从第一行数据可以看出，类别$0$即差评的评论有$81$个被错误地分类到类别$1$ （好评）的文档里。而类别1即好评的评论有$358$个被错误地分类到类别$0$（差评）的文档里。我们还可以把混淆矩阵进行数据可视化处理。

除对角线外，其他地方颜色越浅，说明此处错误越多。可以看到，测试数据集准确性不高，我们还可以详细分析样本数据，找出为什么某类别会被错误地分类到另一种类别里，从而进一步优化模型。在本文将不做展开。
还有很多待改善的地方。

参考：
[1]: 黄永昌.《scikit-learn机器学习：常用算法原理及编程实战》.