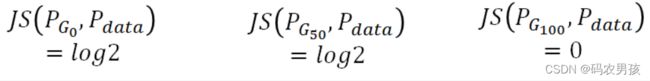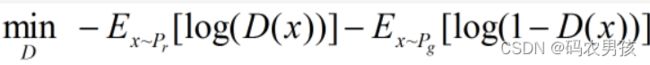WGAN(Wasserstein GAN)看这一篇就够啦，WGAN论文解读

WGAN论文地址：[1701.07875] Wasserstein GAN (arxiv.org)

WGAN解决的问题

原始GAN训练过程中经常遇到的问题：

1. 模式崩溃，生成器生成非常窄的分布，仅覆盖数据分 布中的单一模式。 模式崩溃的含义是生成器只能生成非常相似的样本（例如 ，MNIST中的单个数字），即生成的样本不是多样的。
2. 没有指标可以告诉我们收敛情况。生成器和判别器的 loss并没有告诉我们任何收敛相关信息。当然，我们可以通 过不时地查看生成器生成的数据来监控训练进度。但是， 这是一个手动过程。因此，我们需要有一个可解释的指标 可以告诉我们有关训练的进度。

一句话概括：判别器越好，生成器梯度消失越严重。

      GAN网络训练的重点在于均衡生成器与判别器，若判别器太 强，loss没有再下降，生成器学习不到东西，生成图像的质量 便不会再有提升。

        在最优判别器的下，我们可以把原始GAN定义的生成器loss 等价变换为最小化真实分布与生成分布之间的JS散度。 我们越训练判别器，它就越接近最优，最小化生成器的loss也 就会越近似于最小化真实分布与生成分布之间的JS散度。

关键点就在于如何评价生成图片和真实图片之间的距离

 JS散度存在的问题

如果希望两个分布之间越接近它们的JS散度越小，我们通过 优化JS散度就能将生成分布拉向真实分布，最终以假乱真。 这个希望在两个分布有所重叠的时候是成立的，但是如果两 个分布完全没有重叠的部分，或者它们重叠的部分可忽略， 那它们的JS散度就一直是 log2。

在原始GAN的（近似）最优判别器下，生成器loss面临梯度 消失问题。 也面临优化目标荒谬、梯度不稳定、对多样性与准确性惩罚 不平衡导致mode collapse问题。

原始GAN问题的根源可以归结为两点，

1. 等价优化的距离衡量（JS散度）不合理
2. 生成器随机初始化后的生成分布很难与真实分布有不可 忽略的重叠

Wasserstein GAN（WGAN）就是希望解决上述两个问题

解决原始GAN问题的方法

解决问题的关键在于使用 Wasserstein距离 衡量两个分布之间的距离 Wasserstein距离 优越性在于： 即使两个分布没有任何重叠，也可以反应他们之间的距离。

Wasserstein距离

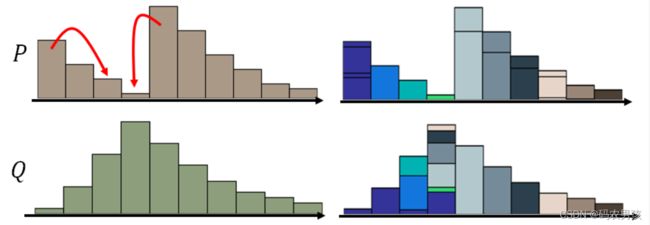
P和Q为两个分布：P分布为一堆土，Q分布为要移到的目标，那么要移动P达到Q，哪种距离更小呢？

最好的移动方案： 

使用Wasserstein距离， 无论两个分布多远，都有梯度，都是可以更新的

WGAN设计 

原始的生成对抗网络，所要优化的目标函数为：

 此目标函数可以分为两部分来看： ①固定生成器 G，优化判别器 D， 则上式可以写成如下形式：

可以转化为最小化形式： 

②固定判别器 D，优化生成器 G，舍去前面的常数，

相当于最小化： 

我们要构建一个判别器 D，使得 D 的参数不超过某个固定的 常数，最后一层是非线性层，并且使下面式子最大化：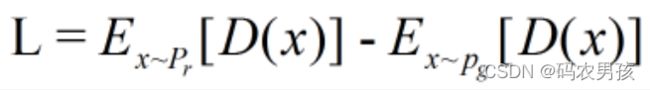

 这是一种数学的近似，同要求梯度变化的不要太猛。那么怎么梯度更新呢？因为D有了限制，无法直接利用SGD。 这里引入一种方法：Weight clipping 就是强制令权重w 限制在c ~ -c之间。在参数更新后，如果 w>c，则令w=c， 如果w<-c，则令w=-c

WGAN的实现

WGAN与原始GAN第一种形式相比，只改了四点：

1. 判别器最后一层去掉sigmoid
2. 生成器和判别器的loss不取log
3. 每次更新判别器的参数之后把它们的值截断到不超过一个 固定常数c
4. 不要用基于动量的优化算法（包括momentum和 Adam），推荐RMSProp

WGAN本作引入了Wasserstein距离，由于它相对KL散度与JS 散度具有优越的平滑特性，理论上可以解决梯度消失问题。接 着通过数学变换将Wasserstein距离写成可求解的形式，利用 一个参数数值范围受限的判别器神经网络来较大化这个形式， 就可以近似Wasserstein距离。

WGAN既解决了训练不稳定的问题，也提供了一个可靠的训 练进程指标，而且该指标确实与生成样本的质量高度相关。