深度学习笔记2之改善神经网络(调参、优化)
目录
- 第二课
-
- week1
-
- 偏差和方差
- 正则化
-
- 为什么L2正则化可以减少过拟合:
- Dropout正则化
- 其他正则化手段
- 归一化输入
- 梯度消失与爆炸
- week2
-
- minibatch梯度下降法
-
- batch size 的选择
- 优化算法
-
- 指数加权平均
- 动量梯度下降
- RMSprop
- Adam
- 学习率衰减
- 局部最优问题
- week3
-
- 调参指导
- BatchNormalization
- softmax
- 个人学习记录,侵删
第二课
week1
偏差和方差
机器学习关键:数据集,选择网络,正则化。来解决偏差和方差
正则化
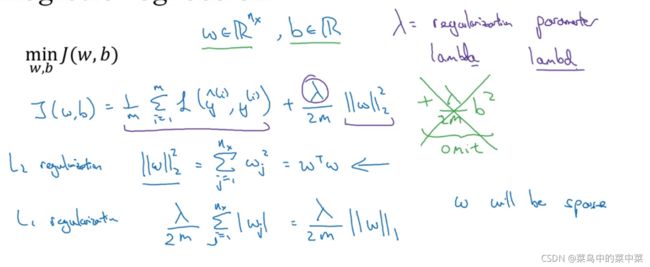
λ \lambda λ 是正则化参数,L2正则化是使用了欧几里德范数(2范数)的平方,L1是加了L1范数,w会是稀疏的,会有很多0,却没有降低太多内存,人们更倾向L2

为什么L2正则化可以减少过拟合:
如果正则化参数变得很大,参数 w 很小, z 也会相对变小,此时忽略 b 的影响, z 会相对变小,
z 的取值范围很小,这个激活函数,也就是曲线函数tanh 会相对呈线性,整个神经网络会计算离线性函数近的值,这个线性函数非常简单,并不是一个极复杂的高度非线性函数(不像前面那个高方差的样子,曲线特别离谱),不会发生过拟合
Dropout正则化
本质: 随机失活
首先要定义向量 d [ 3 ] d^{[3]} d[3]表示一个三层的dropout向量:
d3=np.random.rand(a3.shape[0],a3.shape[1])
然后看它是否小于某数,我们称之为keep-prob,keep-prob是一个具体数字,上个示例中它是0.5,而本例中它是0.8,它表示保留某个隐藏单元的概率,此处keep-prob等于0.8,它意味着消除任意一个隐藏单元的概率是0.2,它的作用就是生成随机矩阵,如果对 a [ 3 ] a^{[3]} a[3]进行因子分解,效果也是一样的。 d [ 3 ] d^{[3]} d[3]是一个矩阵,每个样本和每个隐藏单元,其中 d [ 3 ] d^{[3]} d[3]中的对应值为1的概率都是0.8,对应为0的概率是0.2,随机数字小于0.8。它等于1的概率是0.8,等于0的概率是0.2。
dropout是一种正则化方法,它有助于预防过拟合,因此除非算法过拟合,不然我是不会使用dropout的,所以它在其它领域应用得比较少,主要存在于计算机视觉领域,因为我们通常没有足够的数据,所以一直存在过拟合,这就是有些计算机视觉研究人员如此钟情于dropout函数的原因
缺点: cost函数不再明确。
其他正则化手段
- 数据增强,镜像,旋转裁剪等
- 通过绘制曲线观察,提前停止early stopping
- 不用early stopping,另一种方法就是 L 2 正则化,训练神经网络的时间就可能很长。我发现,这导致超级参数搜索空间更容易分解,也更容易搜索,但是缺点在于,你必须尝试很多正则化参数 λ的值,这也导致搜索大量 λ 值的计算代价太高。
归一化输入
- 零均值化: x − x ˉ x-\bar{x} x−xˉ
- 归一化方差: x / σ 2 x / \sigma^2 x/σ2
为什么归一化输入:将特征值规范化后,使用梯度下降算法,能使cost 更快更好的降低。
如果输入特征处于不同范围内,可能有些特征值从0到1,有些从1到1000,那么归一化特征值就非常重要了。
梯度消失与爆炸
假设激活函数是线性的, y ^ = w l w l − 1 . . . w 1 \hat{y} = w^l w^{l-1}...w^1 y^=wlwl−1...w1
如果w>1,y 的值将爆炸式增长。相反,以指数级递减
权重初始化

梯度的数值逼近(不懂插眼)
梯度检验(不懂插眼)

week2
minibatch梯度下降法
样本太多,让小部分先进行梯度下降。可以把训练集分割为小一点的子集训练,这些子集被取名为mini-batch。
batch是一次性处理所有样本。
使用batch梯度下降法,一次遍历训练集只能让你做一个梯度下降,使用mini-batch梯度下降法,一次遍历训练集,能让你做5000个梯度下降。
实际上你选择的mini-batch大小在二者之间,大小在1和 m 之间,而1太小了, m 太大了,原因在于如果使用batch梯度下降法,mini-batch的大小为 m,每个迭代需要处理大量训练样本,该算法的主要弊端在于特别是在训练样本数量巨大的时候,单次迭代耗时太长。如果训练样本不大,batch梯度下降法运行地很好。
如果等于1,是SGD,效率低,因为每次只是处理一个,不能享受向量化带来的速度提升。
实际上,选择中间大小的合适,当持续靠近底部时,可以降低学习率。
batch size 的选择
一般来说 Batch_Size 越大,其确定的下降方向越准,引起训练震荡越小。但是Batch_Size 增大到一定程度,其确定的下降方向已经基本不再变化。也就说容易陷入局部最优(也可以理解为如果batch_size很大会导致学习到的特征偏向于整体特征,学习到的内容不够)
batchsize和时间、准确率的关系:论文Accurate, Large Minibatch SGD
本文在ImageNet数据集上进行训练实验,一直将batch增加到8192(on 256GPUs),将训练的时间减少到1h。所用到的核心方法就是线性缩放原则。
Linear Scaling Rule: When the minibatch size is multiplied by k, multiply the learning rate by k
优化算法
展示几个优化算法,比梯度下降法快
指数加权平均
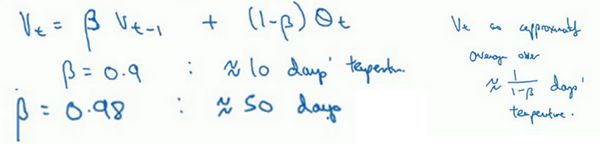
1 1 − β \frac{1}{1-β} 1−β1是平均了多少个样本。
=0.9,就是10个
=0.98 ,就是50个

偏差修正:从紫线变成绿线
在机器学习中,在计算指数加权平均数的大部分时候,大家不在乎执行偏差修正,因为大部分人宁愿熬过初始时期,拿到具有偏差的估测,然后继续计算下去。如果你关心初始时期的偏差,在刚开始计算指数加权移动平均数的时候,偏差修正能帮助你在早期获取更好的估测。
动量梯度下降
Momentum
和指数加权平均异曲同工

效果:纵轴方向的摆动变小了,横轴方向运动更快,因此你的算法走了一条更加直接的路径,在抵达最小值的路上减少了摆动。
紫色变蓝色变红色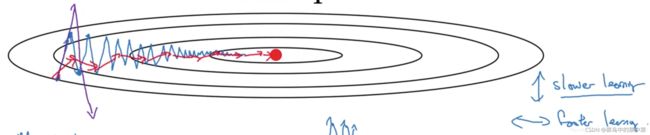
RMSprop
Adam
学习率衰减
加快学习算法的一个办法就是随时间慢慢减少学习率,我们将之称为学习率衰减
1.
2.(1)指数衰减、(2)其他、(3)离散下降
3.手动调整
学习率衰减并不是我尝试的要点,设定一个固定的 α \alphaα ,然后好好调整,会有很大的影响,学习率衰减的确大有裨益,有时候可以加快训练,但它并不是我会率先尝试的内容
局部最优问题
首先,你不太可能困在极差的局部最优中,条件是你在训练较大的神经网络,存在大量参数,并且成本函数 J JJ 被定义在较高的维度空间。
第二点,平稳段是一个问题,这样使得学习十分缓慢,这也是像Momentum或是RMSprop,Adam这样的算法,能够加速学习算法的地方。在这些情况下,更成熟的优化算法,如Adam算法,能够加快速度,让你尽早往下走出平稳段。
原文链接:https://blog.csdn.net/weixin_36815313/article/details/105434823
week3
调参指导
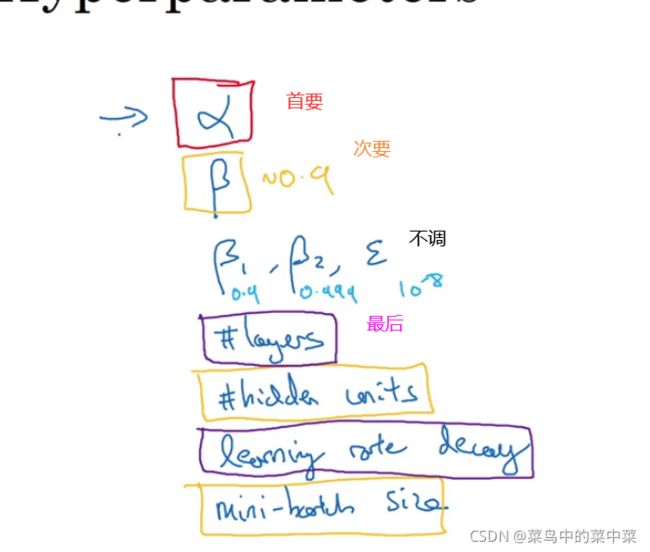
如果你尝试调整一些超参数,该如何选择调试值呢?
推荐采用下面的做法,随机取值,然后采用由粗糙到精细的策略。

在合理的区间不能用线性轴取值,具体动量、学习率、adam等参数调整原文
BatchNormalization
本质是归一化每层后a值,其实是z值。 a = g ( z ) a = g(z) a=g(z)

bn由均值和方差控制,其他学习参数可以是任意。
过程: x w , b − > z γ , β − > z n − > a = g ( z n ) x^{w,b} -> z^{γ,β} ->z^n -> a=g(z^n) xw,b−>zγ,β−>zn−>a=g(zn)

为什么BN奏效:
Batch归一化有效的第二个原因是,它可以使权重比你的网络更滞后或更深层,比如,第10层的权重更能经受得住变化,相比于神经网络中前层的权重,比如第1层
后面需要时在仔细学习。
softmax
从z到a的计算过程中,加入一个临时变量t,是一个C(类别数)x1向量。

然后计算a,a = t/sum(t),算出来是一个向量,代表每个类的概率。


