自动驾驶横向控制 LQR 算法推导及仿真学习笔记

目录

1、车辆动力学模型

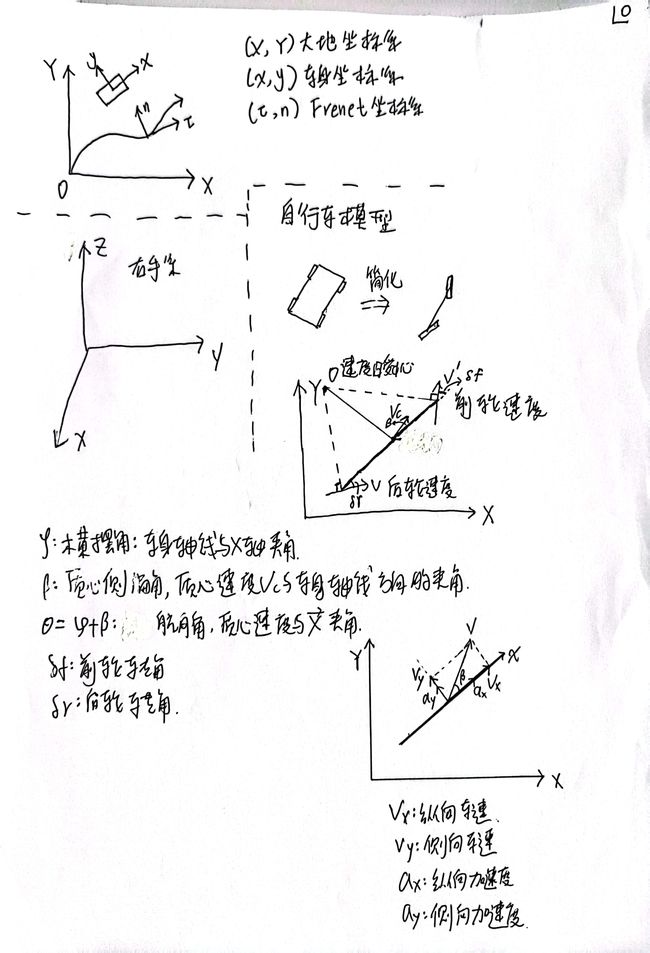
1.1 Frenet 坐标系

1.2 横向误差模型

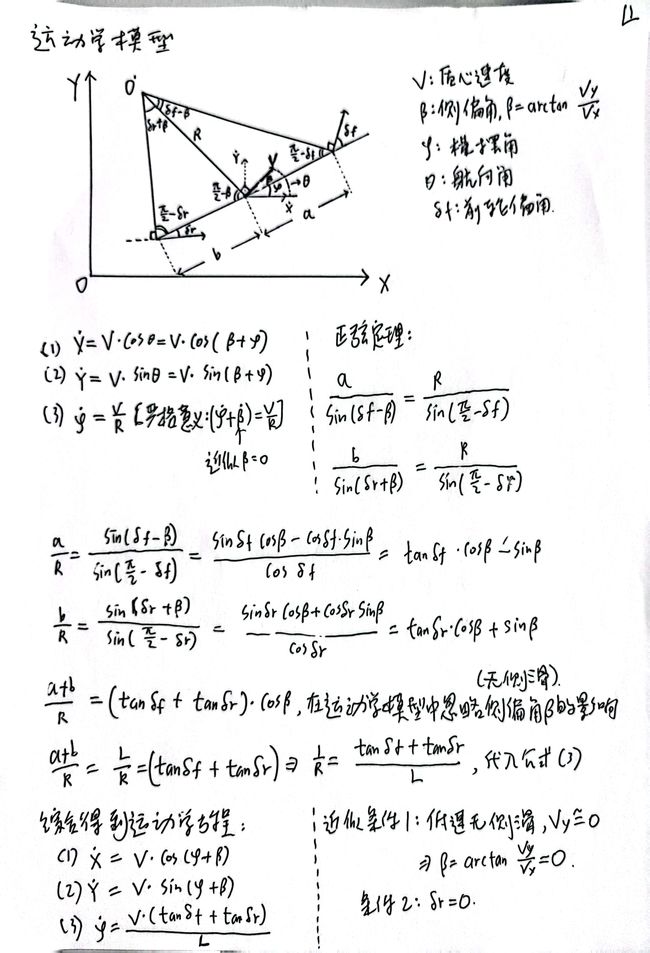
1.2.1 运动学模型

1.2.2 自行车模型

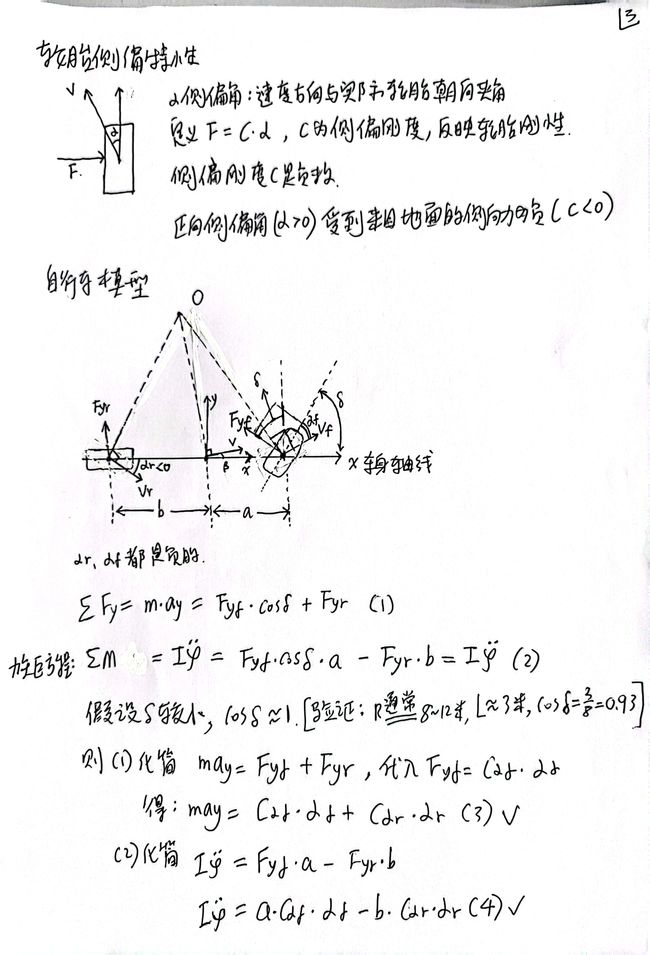
1.2.3 轮胎侧偏特性

2、LQR 及前馈控制算法

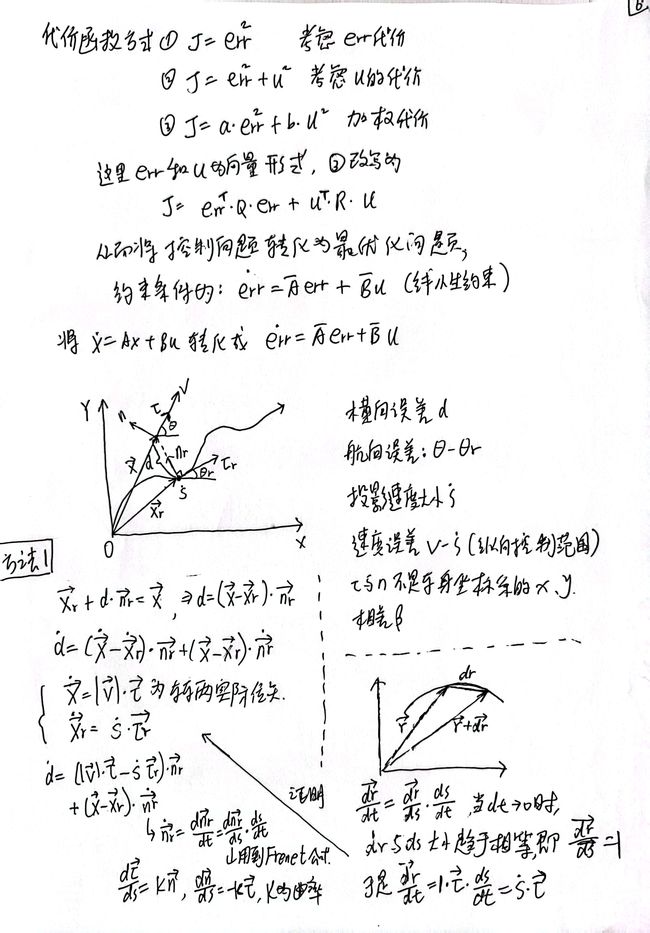
2.1 Frenet 坐标系下的连续 LQR

2.2 离散 LQR

2.2.1 前向欧拉法、中点欧拉法离散化

2.2.2 拉格朗日乘子法 

2.2.3 对 x、u、λ 求偏导

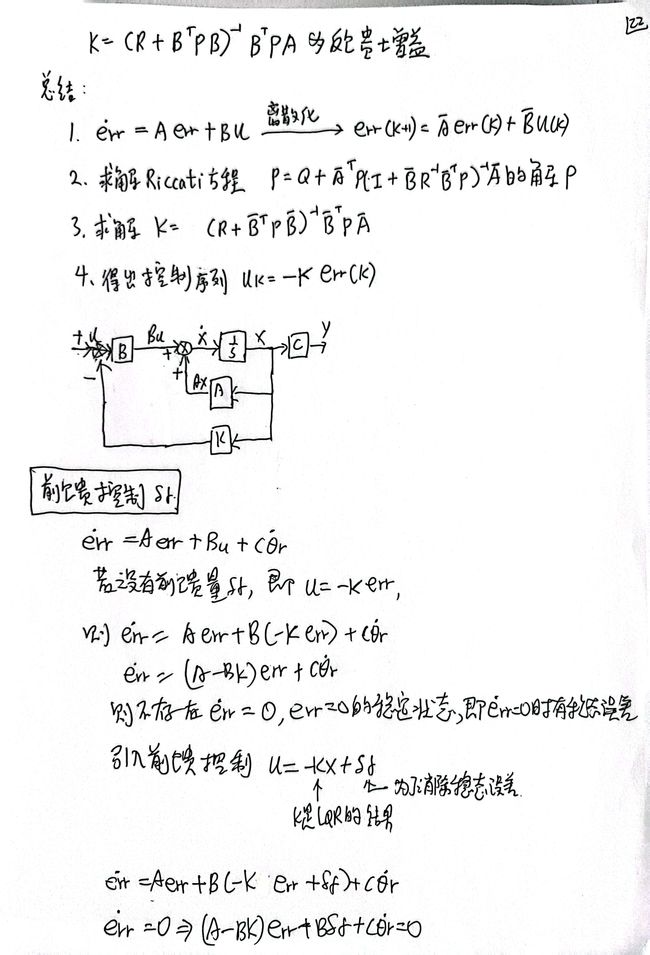
2.2.4 递推得到 Riccati 方程

2.2.5 Riccati 方程求解

2.3 控制序列 uk 整合 

2.3.1 前馈控制量 δf

2.3.2 当前位置与规划路径点间的误差量 err 

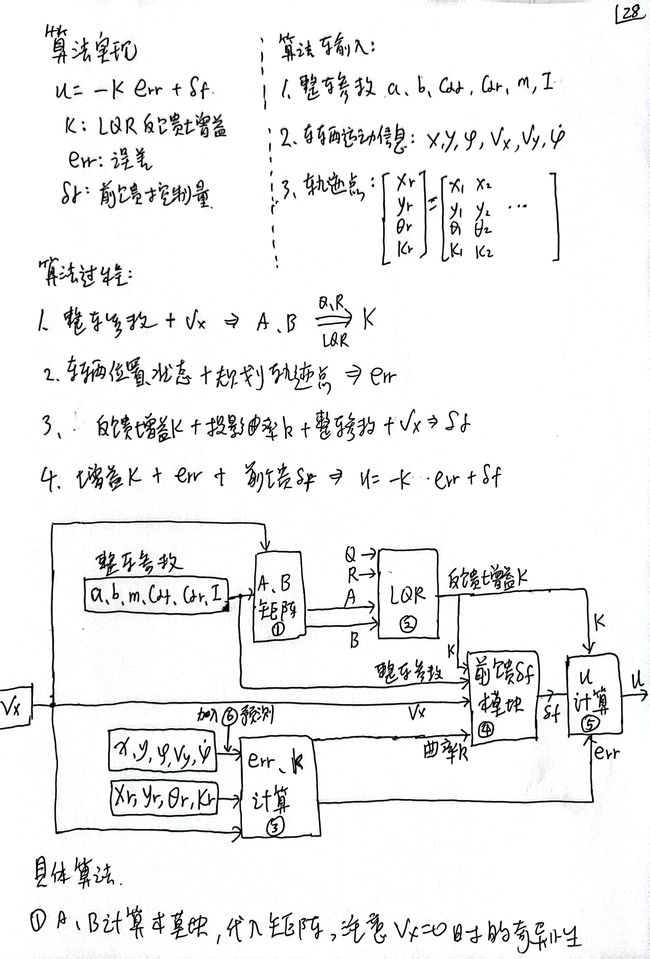
2.4 算法过程总结

3、MATLAB + Carsim 仿真

3.1 Carsim 配置

3.1.1 车辆参数配置

3.1.2 IO 通道

3.1.3 路况设置

3.1.4 规划路径点

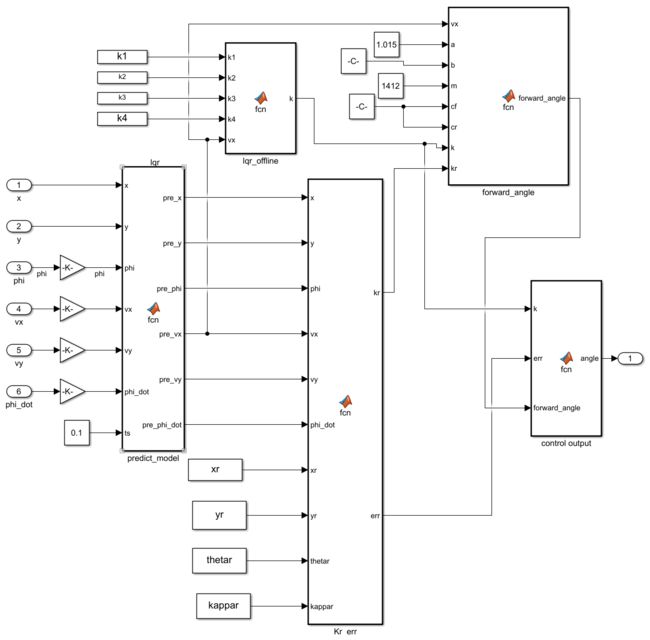
3.2 Simulink 搭建

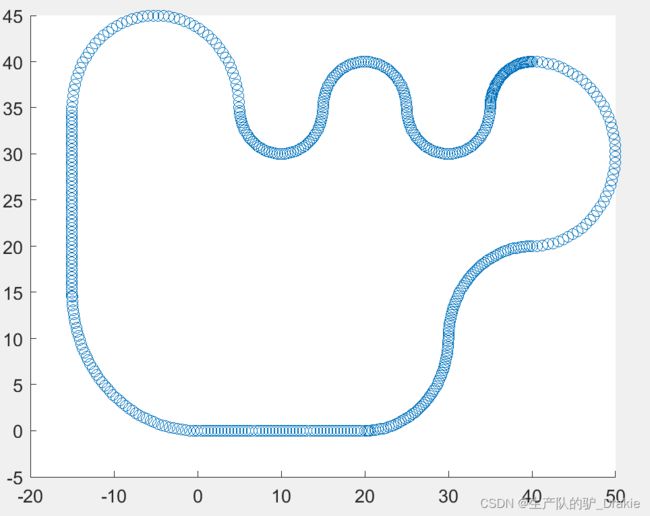
3.2.1 生成轨迹规划点

3.2.2 预瞄路径点 preview 计算模块

3.2.3 误差 err、投影点曲率 k 计算模块

3.2.4 离线计算 LQR 反馈增益 K

3.2.5 dlqr 离线查表

3.2.6 前馈控制量 δf 计算模块

3.2.7 控制序列 uk 整合

3.3 控制效果与优化

3.3.1 Carsim 动画效果

3.3.2 控制量抖动优化

3.3.2 控制量突变优化

---

1、车辆动力学模型

1.1 Frenet 坐标系

1.2 横向误差模型

1.2.1 运动学模型

1.2.2 自行车模型

1.2.3 轮胎侧偏特性

2、LQR 及前馈控制算法

2.1 Frenet 坐标系下的连续 LQR

2.2 离散 LQR

2.2.1 前向欧拉法、中点欧拉法离散化

2.2.2 拉格朗日乘子法 

2.2.3 对 x、u、λ 求偏导

2.2.4 递推得到 Riccati 方程

2.2.5 Riccati 方程求解

2.3 控制序列 uk 整合 

2.3.1 前馈控制量 δf

2.3.2 当前位置与规划路径点间的误差量 err 

2.4 算法过程总结

3、MATLAB + Carsim 仿真

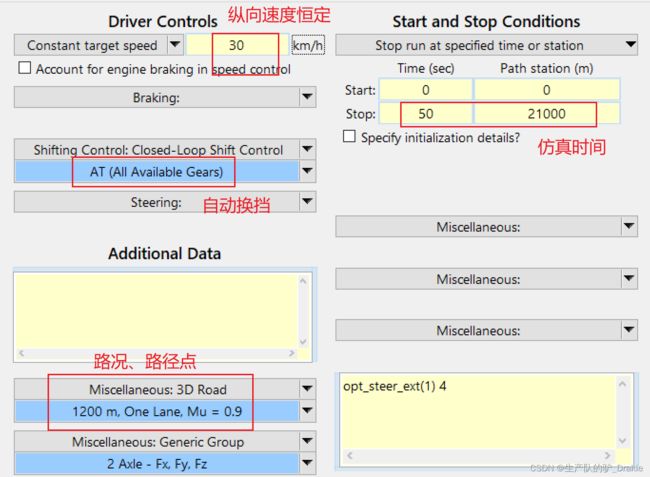
carsim 版本为 2019，MATLAB 版本为 2018a 

3.1 Carsim 配置

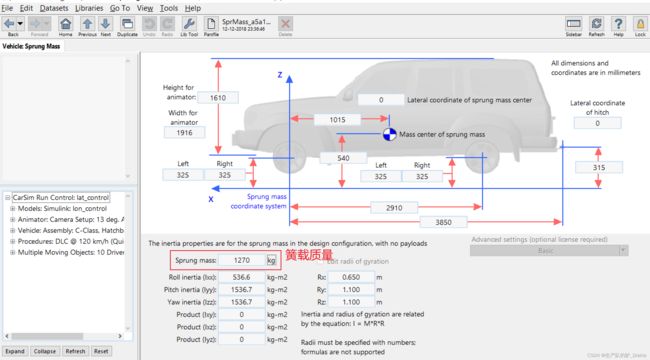
3.1.1 车辆参数配置

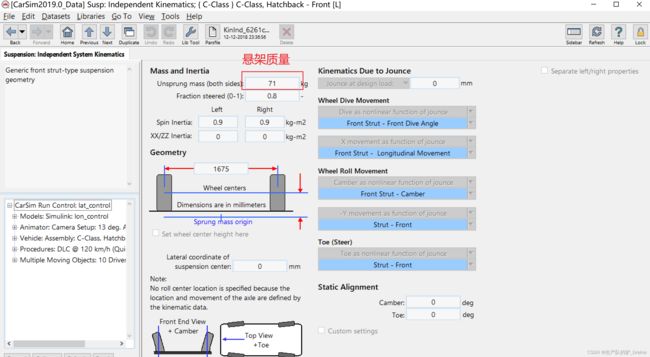
选择 C 级车型

查看悬架质量

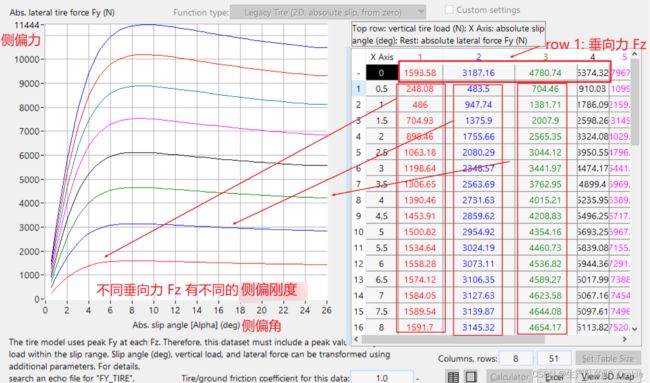
理解轮胎侧偏刚度曲线

3.1.2 IO 通道

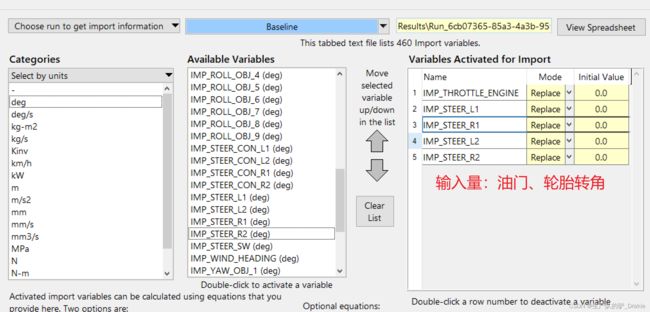
输入通道设置

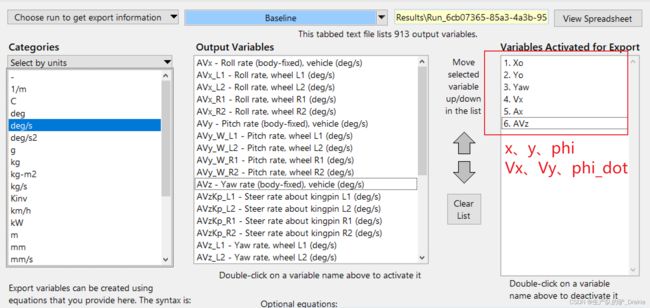
输出通道设置

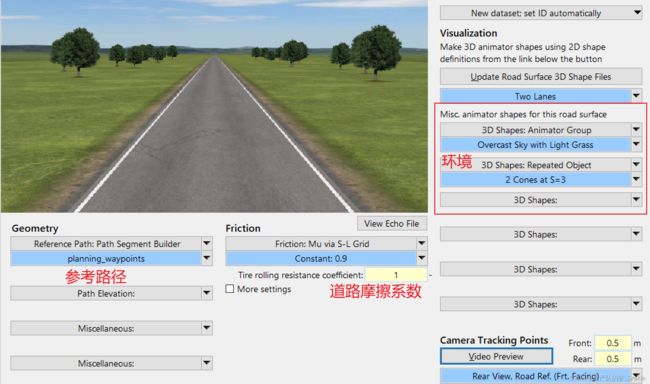
3.1.3 路况设置

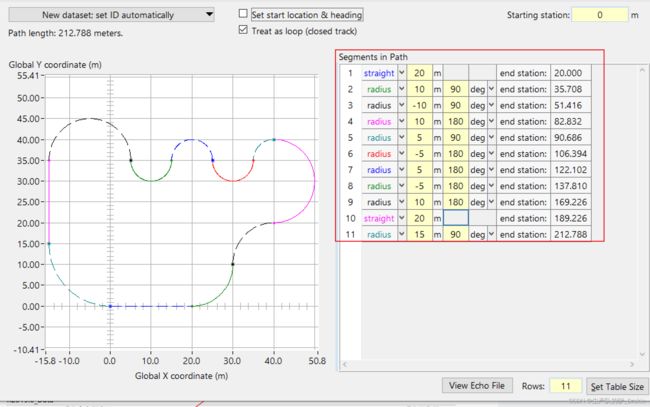
3.1.4 规划路径点

设置路径

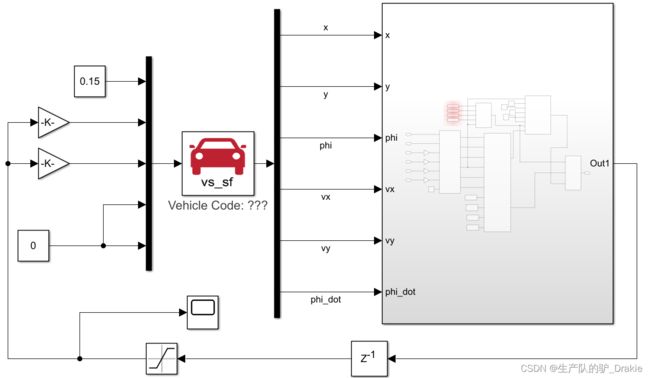
3.2 Simulink 搭建

子模块预览

3.2.1 生成轨迹规划点

count=50;
[x1,y1,theta1,kr1]=straight([0,0],[20,0],0,count);
[x2,y2,theta2,kr2]=arc([20,0],[30,10],0,pi/2,count);
[x3,y3,theta3,kr3]=arc([30,10],[40,20],pi/2,0,count);
[x4,y4,theta4,kr4]=arc([40,20],[40,40],0,pi,count);
[x5,y5,theta5,kr5]=arc([40,40],[35,35],pi,3*pi/2,count);
[x6,y6,theta6,kr6]=arc([35,35],[25,35],3*pi/2,pi/2,count);
[x7,y7,theta7,kr7]=arc([25,35],[15,35],pi/2,3*pi/2,count);
[x8,y8,theta8,kr8]=arc([15,35],[5,35],3*pi/2,pi/2,count);
[x9,y9,theta9,kr9]=arc([5,35],[-15,35],pi/2,3*pi/2,count);
[x10,y10,theta10,kr10]=straight([-15,35],[-15,15],3*pi/2,count);
[x11,y11,theta11,kr11]=arc([-15,15],[0,0],3*pi/2,2*pi,count);
xr=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11];
yr=[y1,y2,y3,y4,y5,y6,y7,y8,y9,y10,y11];
thetar=[theta1,theta2,theta3,theta4,theta5,theta6,theta7,theta8,theta9,theta10,theta11];
kappar=[kr1,kr2,kr3,kr4,kr5,kr6,kr7,kr8,kr9,kr10,kr11];

scatter(xr,yr);

function[xr,yr,thetar,kr]=straight(init_coord,end_coord,init_angle,count)
delta_x=(end_coord(1)-init_coord(1))/(count-1);
delta_y=(end_coord(2)-init_coord(2))/(count-1);
for i=1:count
    xr(i)=init_coord(1)+delta_x*i;
    yr(i)=init_coord(2)+delta_y*i;
    thetar(i)=init_angle;
    kr(i)=0;
end      
end

function[xr,yr,thetar,kr]=arc(init_coord,end_coord,init_angle,end_angle,count)
    L=sqrt((init_coord(1)-end_coord(1))^2+(init_coord(2)-end_coord(2))^2);
    R=L/sqrt(2*(1-cos(end_angle-init_angle)));
    delta_angle=(end_angle-init_angle)/(count-1) ;
  
       for i=1:count
           if delta_angle>0
               xr(i)=init_coord(1)-R*sin(init_angle)+R*sin(init_angle+delta_angle*(i-1));
               yr(i)=init_coord(2)+R*cos(init_angle)-R*cos(init_angle+delta_angle*(i-1));
               thetar(i)=init_angle+delta_angle*i;
               kr(i)=1/R;
           else
               xr(i)=init_coord(1)+R*sin(init_angle)-R*sin(init_angle+delta_angle*(i-1));

               yr(i)=init_coord(2)-R*cos(init_angle)+R*cos(init_angle+delta_angle*(i-1));
               thetar(i)=init_angle+delta_angle*i;
               kr(i)=-1/R;
           end               
       end  
end

执行 m 文件，生成轨迹图像

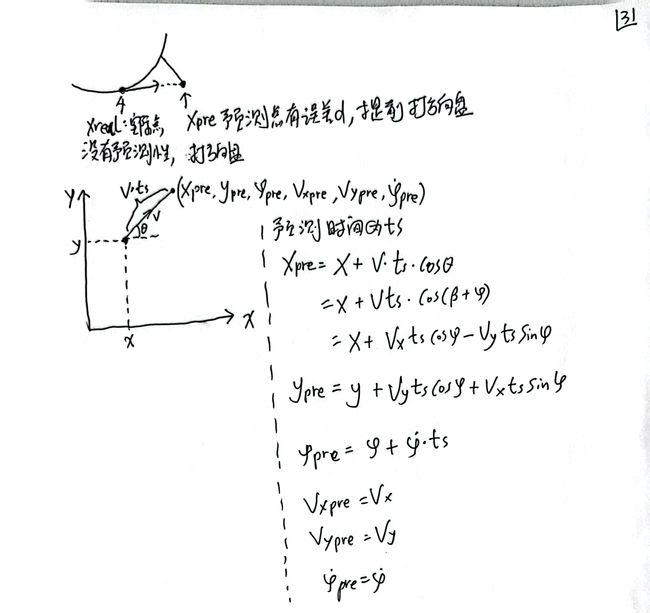
3.2.2 预瞄路径点 preview 计算模块

% 预测模块
function [pre_x, pre_y, pre_phi, pre_vx, pre_vy, pre_phi_dot] = fcn(x, y, phi, vx, vy, phi_dot, ts)
    pre_x = x + vx * ts * cos(phi) - vy * ts * sin(phi);
    pre_y = y + vy * ts * cos(phi) + vx * ts * sin(phi);
  pre_phi = phi + phi_dot * ts;
   pre_vx = vx;
   pre_vy = vy;
 pre_phi_dot = phi_dot; 
end

3.2.3 误差 err、投影点曲率 k 计算模块

function [kr,err] = fcn(x,y,phi,vx,vy,phi_dot,xr,yr,thetar,kappar)
    n=length(xr); % 规划点的长度
    d_min = (x-xr(1))^2 +  (y-yr(1))^2; % 找出最短距离
    min = 1; % 最短点的序号设为 1
    for i=1:n
        d = (x-xr(i))^2 + (y-yr(i))^2;
        if d < d_min
            d_min = d;
            min = i;
        end
    end
   dmin = min;
   tor = [cos(thetar(dmin));  sin(thetar(dmin))];
   nor = [-sin(thetar(dmin)); cos(thetar(dmin))];
   d_err = [x - xr(dmin); y - yr(dmin)];
   ed = nor' * d_err;
   es = tor' * d_err;
   % projection_point_thetar = thetar(dmin);
     projection_point_thetar = thetar(dmin) + kappar(dmin) * es;
   ed_dot = vy * cos(phi - projection_point_thetar) + vx * sin(phi - projection_point_thetar);
   ephi = sin(phi - projection_point_thetar);
   
   s_dot = vx * cos(phi - projection_point_thetar) - vy * sin(phi - projection_point_thetar);
   s_dot = s_dot / (1 - kappar(dmin) * ed);
   ephi_dot = phi_dot - kappar(dmin) * s_dot;
   kr = kappar(dmin);
   err = [ed; ed_dot; ephi; ephi_dot];
end

3.2.4 离线计算 LQR 反馈增益 K

这里需要先执行一次 m 文件，生成 K 值

cf = -110000;
cr = cf;
m = 1412;
Iz = 1537.7;
a = 1.015;
b = 2.910 - a;
k = zeros(5000, 4);
for i=1:5000
    vx = 0.01 + 0.01 *  i;
    A = [0, 1, 0, 0;
        0, (cf+cr)/(m*vx), -(cf+cr)/m, (a*cf-b*cr)/(m*vx);
        0,0,0,1;
        0,(a*cf - b*cr)/(Iz*vx),-(a*cf-b*cr)/Iz,(a*a*cf+b*b*cr)/(Iz*vx)];
    B = [0;
        -cf/m;
        0;
        -a*cf/Iz];
    Q = eye(4);
    R = 100;
    k(i,:) = lqr(A,B,Q,R);
end
k1 = k(:,1)';
k2 = k(:,2)';
k3 = k(:,3)';
k4 = k(:,4)';

3.2.5 dlqr 离线查表

function k = fcn(k1,k2,k3,k4,vx)
  if abs(vx) < 0.01
      k = [0,0,0,0];
  else
      index = round(vx / 0.01);
      k = [k1(index), k2(index), k3(index), k4(index)];
  end
end

3.2.6 前馈控制量 δf 计算模块

function forward_angle = fcn(vx, a, b, m, cf, cr, k, kr)
  forward_angle = kr*(a+b-b*k(3)-(m*vx*vx/(a+b))*((b/cf)+(a/cr)*k(3)-(a/cr)));
end

3.2.7 控制序列 uk 整合

function angle = fcn(k, err, forward_angle)
  angle = -k * err + forward_angle;
end

3.3 控制效果与优化

3.3.1 Carsim 动画效果

鸟瞰视角

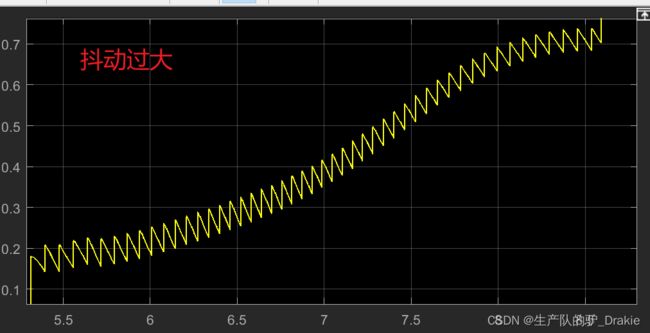
3.3.2 控制量抖动优化

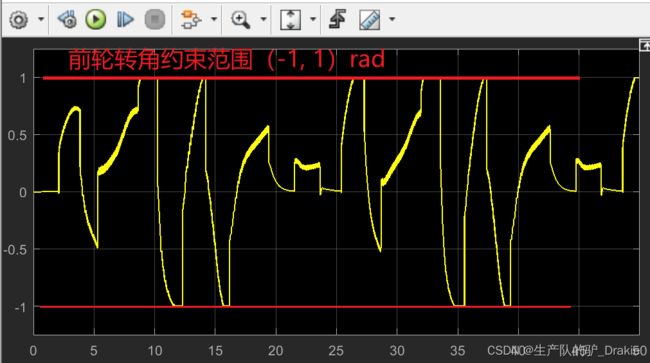
控制量波形受到饱和约束，前轮转角变化范围为 ±1 rad

问题描述：控制量抖动过大，即方向盘不平稳

原因：在 err 和 曲率计算模块中，投影点的航向角用匹配点的航向角近似代替，导致计算结果反复不定，修正后重新执行。

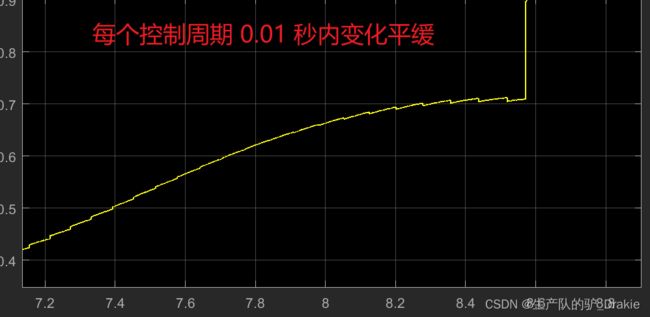
改善结果：控制量 u 抖动明显减少

控制量在每个周期内的变化率较为平缓

3.3.2 控制量突变优化

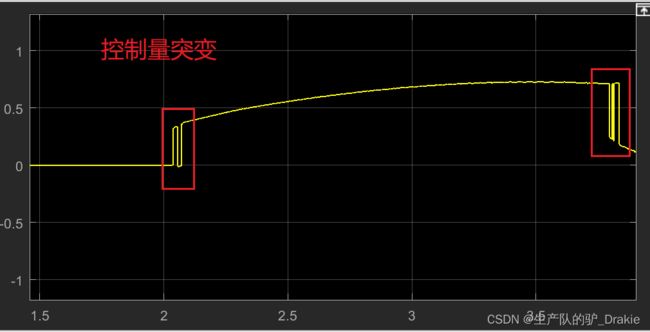
问题描述：在道路曲率变化处的控制量存在突变现象

原因：规划路径的曲率不连续，路径点本身曲率就存在突变，没有过渡曲率

解决方法 1：在曲率突变处进行插值，保证连接处曲率的一阶导数与二阶导数都连续，在实际路况中大多数的公路设计都是连续曲率。

解决方法 2：增大 LQR 控制器中 R 的值，即增大ｕ的惩罚权重，使ｕ变化减缓。