隆华爱读书我不爱读书所以我没书读

基于OpenCV的图像透视变换详解(从理论到实现再到实践)

一、仿射变换与透视变换

一直无法理解两种仿射变换与透视变换的区别，因此详细学习了两种变换的具体细节，重新书写了公式，并给出自己的一些看法。

1.仿射变换

可以认为，仿射变换是透视变换的一种特例。

仿射变换是一种二维坐标到二维坐标之间的线性变换，也就是只涉及一个平面内二维图形的线性变换。

图形的平移、旋转、错切、放缩都可以用仿射变换的变换矩阵表示。

它保持了二维图形的两种性质：

① “平直性”：直线经过变换之后依然是直线。一条直线经过平移、旋转、错切、放缩都还是一条直线。

②“平行性”：变换后平行线依然是平行线，且直线上点的位置顺序不变。

直观的感受就是，我们在电脑上对一张图片进行拖动、翻转、拉伸等等操作，看这一张图片的视角是不会变的。

任意的仿射变换都能表示为一个坐标向量乘以一个矩阵的形式，下面是几种仿射变换的矩阵形式。

放缩：

$\begin{equation} \left[ \begin{array}{c} x'\\ y'\\ \end{array} \right ] = \left[ \begin{array}{c} T_{x}x\\ T_{y}y\\ \end{array} \right ] = \left[ \begin{array}{ccc} T_{x}& 0 \\ 0& T_{y} \\ \end{array} \right ] \left[ \begin{array}{c} x\\ y\\ \end{array} \right ] \end{equation}$

旋转：

$\begin{equation} \left[ \begin{array}{c} x'\\ y'\\ \end{array} \right ] = \left[ \begin{array}{c} xcos\theta-ysin\theta\\ xsin\theta+ycos\theta\\ \end{array} \right ] = \left[ \begin{array}{cc} cos\theta& -sin\theta \\ sin\theta& cos\theta \\ \end{array} \right ] \left[ \begin{array}{c} x\\ y\\ \end{array} \right ] \end{equation}$

错切：

$\begin{equation} \left[ \begin{array}{c} x'\\ y'\\ \end{array} \right ] = \left[ \begin{array}{c} x+ytan\phi\\ y+xtan\varphi\\ \end{array} \right ] = \left[ \begin{array}{cc} 1& tan\phi \\ tan\varphi& 1 \\ \end{array} \right ] \left[ \begin{array}{c} x\\ y\\ \end{array} \right ] \end{equation}$

上面几种变换都可以直接只用2x2矩阵变换，但是平移无法做到，因为在2x2矩阵中无论怎么相乘都无法变换出一个常数量。因此需要将原本的2维坐标向量变成齐次坐标，也就是用3维向量来表示2维向量。

$\left[ \begin{array}{c} x\\ y\\ \end{array} \right ] => \left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ]$

平移：

$\begin{equation} \left[ \begin{array}{c} x'\\ y'\\ \end{array} \right ] = \left[ \begin{array}{c} x+T_{x}\\ y+T_{y}\\ \end{array} \right ] = \left[ \begin{array}{ccc} 1& 0 &T_{x}\\ 0& 1 &T_{y}\\ \end{array} \right ] \left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ] \end{equation}$

变成齐次坐标后，为了实现原本2x2矩阵的放缩、旋转、错切的变换，只需要令 $T_{x}=T_{y}=0$ 即可。

上面的变换都是线性变换，因此仿射变换可以用以下通式来表示，也就是网上常见到的形式：

$\begin{equation} \left[ \begin{array}{c} x'\\ y'\\ \end{array} \right ] = \left[ \begin{array}{c} a_{11}x+a_{12}y+a_{13}\\ a_{21}x+a_{22}y+a_{23}\\ \end{array} \right ] = \left[ \begin{array}{ccc} a_{11}& a_{12}&a_{13}\\ a_{21}& a_{22} &a_{23}\\ \end{array} \right ] \left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ] \end{equation}$

此时仿射变换的变换矩阵 $T= \left[ \begin{array}{ccc} a_{11}& a_{12}&a_{13}\\ a_{21}& a_{22} &a_{23}\\ \end{array} \right ]$ 是2x3矩阵。

因此坐标变换的方程组如下：

$\begin{equation} \left\{ \begin{matrix}{} x'=a_{11}x+a_{12}y+a_{13} \\ y'=a_{21}x+a_{22}y+a_{23} \\ \end{matrix} \right. \end{equation}$

可以看到有6个未知的系数，需要3对映射点（前提是相互独立）才能求解。这不难理解，6个变量自然需要至少列6个等式才可计算，而1对映射点可以提供2个等式。

同时3个点唯一确定一个平面，另外的3个映射点由于是线性变换也必然在同一个平面内，所以可以说仿射变换是平面内的图形变换。

2.透视变换

透视变换是将图片投影到一个新的视平面，也称作投影映射。

它是二维到三维，再到另一个二维空间的映射。

相对于仿射变换，它不仅仅是线性变换。它提供了更大的灵活性，可以将一个四边形区域映射到另一个四边形区域。

透视变换也是通过矩阵乘法实现的，使用的是一个3x3的矩阵，矩阵的前两行与仿射矩阵相同，这意味着仿射变换的所有变换透视变换也可以实现。而第三行则用于实现透视变换。

透视变换也使用了齐次坐标来表示二维向量：

$\begin{equation} \left[ \begin{array}{c} x'\\ y'\\ z'\\ \end{array} \right ] = \left[ \begin{array}{ccc} a_{11}& a_{12} &a_{13}\\ a_{21}& a_{22} &a_{23}\\ a_{31}& a_{32} &a_{33}\\ \end{array} \right ] \left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ] \end{equation}$

此时透视变换的变换矩阵 $T= \left[ \begin{array}{ccc} a_{11}& a_{12} &a_{13}\\ a_{21}& a_{22} &a_{23}\\ a_{31}& a_{32} &a_{33}\\ \end{array} \right ]$ 是3x3矩阵

透视变换得到的 $\left[ \begin{array}{c} x'\\ y'\\ z'\\ \end{array} \right ]$ 不是最后的坐标，需要进一步转化：

$\begin{equation} \left[ \begin{array}{c} x'\\ y'\\ z'\\ \end{array} \right ] = z' \left[ \begin{array}{c} \frac{x'}{z'}\\ \frac{y'}{z'}\\ 1\\ \end{array} \right ] \end{equation}$

$\left[ \begin{array}{c} \frac{x'}{z'}\\ \frac{y'}{z'}\\ 1\\ \end{array} \right ]$ 才是最后转化后的坐标，即：

$\begin{equation} \left[ \begin{array}{c} x''\\ y''\\ 1\\ \end{array} \right ] = \left[ \begin{array}{c} \frac{x'}{z'}\\ \frac{y'}{z'}\\ 1\\ \end{array} \right ] \end{equation}$

事实上这里就可以明白为什么仿射变换是透视变换的一种特例。因为如果仿射变换后的坐标向量也用齐次坐标 $\left[ \begin{array}{c} x'\\ y'\\ 1\\ \end{array} \right ]$ 表示，2x3矩阵转为3x3矩阵可以看作是：

$T_{affine}= \left[ \begin{array}{ccc} a_{11}& a_{12} &a_{13}\\ a_{21}& a_{22} &a_{23}\\ 0& 0 &1\\ \end{array} \right ]$

此时仿射变换与透视变换的形式得到统一，仿射变换过程视为如下：

$\begin{equation} \left[ \begin{array}{c} x'\\ y'\\ 1\\ \end{array} \right ] = \left[ \begin{array}{ccc} a_{11}& a_{12} &a_{13}\\ a_{21}& a_{22} &a_{23}\\ 0& 0 &1\\ \end{array} \right ] \left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ] \end{equation}$

所以仿射变换只是透视变换矩阵第三行为 $\left[ \begin{matrix} 0&0&1\\ \end{matrix} \right ]$ 的一种特殊情况。此时已经扩展到3维向量，其实我们也可以理解为仿射变换是在空间坐标系的平面上进行的平面内的图像变换，即z方向的值无论怎么变都是1，始终都限制在平面内。

再回到透视变换，整个透视变换的过程如下：

$\begin{equation} \begin{aligned} \left[ \begin{array}{c} x''\\ y''\\ 1\\ \end{array} \right ] = \left[ \begin{array}{c} \frac{x'}{z'}\\ \frac{y'}{z'}\\ 1\\ \end{array} \right ] = \frac{1}{z'} \left[ \begin{array}{c} x'\\ y'\\ z'\\ \end{array} \right ] = \frac{1}{z'} \left[ \begin{array}{ccc} a_{11}& a_{12} &a_{13}\\ a_{21}& a_{22} &a_{23}\\ a_{31}& a_{32} &a_{33}\\ \end{array} \right ] \left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ] \\= \frac{1}{a_{31}x+a_{32}y+a_{33}} \left[ \begin{array}{ccc} a_{11}& a_{12} &a_{13}\\ a_{21}& a_{22} &a_{23}\\ a_{31}& a_{32} &a_{33}\\ \end{array} \right ] \left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ] \end{aligned} \end{equation}$

因此坐标变换的方程组如下：

$\begin{equation} \left\{ \begin{matix}{} x''=\frac{x'}{z'}=\frac{a_{11}x+a_{12}y+a_{13}}{a_{31}x+a_{32}y+a_{33}} \\ y''=\frac{y'}{z'}=\frac{a_{21}x+a_{22}y+a_{23}}{a_{31}x+a_{32}y+a_{33}} \\ \end{matix} \right. \end{equation}$

共有9个未知参数，可以进一步简化为8个未知参数，也就是网上常见的形式。

这里我的思路是：证明变换矩阵 $T= \left[ \begin{array}{ccc} a_{11}& a_{12} &a_{13}\\ a_{21}& a_{22} &a_{23}\\ a_{31}& a_{32} &a_{33}\\ \end{array} \right ]$ 与变换矩阵 $T'=kT= \left[ \begin{array}{ccc} ka_{11}& ka_{12} &ka_{13}\\ ka_{21}& ka_{22} &ka_{23}\\ ka_{31}& ka_{32} &ka_{33}\\ \end{array} \right ]$ (k是常数)，所表示的变换是等价的。

将变换矩阵设为，代入运算：

$\begin{equation} \left[ \begin{array}{c} x'\\ y'\\ z'\\ \end{array} \right ] =T' \left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ] =kT \left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ] = \left[ \begin{array}{ccc} ka_{11}& ka_{12} &ka_{13}\\ ka_{21}& ka_{22} &ka_{23}\\ ka_{31}& ka_{32} &ka_{33}\\ \end{array} \right ] \left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ] \end{equation}$

得到方程组如下：

$\begin{equation} \left\{ \begin{matix}{} x''=\frac{k(a_{11}x+a_{12}y+a_{13})}{k(a_{31}x+a_{32}y+a_{33})}=\frac{a_{11}x+a_{12}y+a_{13}}{a_{31}x+a_{32}y+a_{33}} \\ y''=\frac{k(a_{21}x+a_{22}y+a_{23})}{k(a_{31}x+a_{32}y+a_{33})}=\frac{a_{21}x+a_{22}y+a_{23}}{a_{31}x+a_{32}y+a_{33}} \\ \end{matix} \right. \end{equation}$

可以发现最后计算出来的与使用变换矩阵计算出来的结果是一样的。

因此对于 $T= \left[ \begin{array}{ccc} a_{11}& a_{12} &a_{13}\\ a_{21}& a_{22} &a_{23}\\ a_{31}& a_{32} &a_{33}\\ \end{array} \right ]$ ，我们总可以等价为 $\frac{T}{a_{33}}= \left[ \begin{array}{ccc} \frac{a_{11}}{a_{33}}& \frac{a_{12}}{a_{33}} &\frac{a_{13}}{a_{33}}\\ \frac{a_{21}}{a_{33}}& \frac{a_{22}}{a_{33}} &\frac{a_{23}}{a_{33}}\\ \frac{a_{31}}{a_{33}}& \frac{a_{32}}{a_{33}} &1\\ \end{array} \right ]$ 所带来的转换。

对上述变量重新命名即可得到变换矩阵T：

$T= \left[ \begin{array}{ccc} b_{11}& b_{12} &b_{13}\\ b_{21}& b_{22} &b_{23}\\ b_{31}& b_{32} &1\\ \end{array} \right ]$

此时只有8个未知参数，变换方程组也变成如下：

$\begin{equation} \left\{ \begin{matix}{} x''=\frac{x'}{z'}=\frac{b_{11}x+b_{12}y+b_{13}}{b_{31}x+b_{32}y+1} \\ y''=\frac{y'}{z'}=\frac{b_{21}x+b_{22}y+b_{23}}{b_{31}x+b_{32}y+1} \\ \end{array} \right. \end{equation}$

求解8个未知数需要8个等式，1组映射点提供2个等式，所以需要找到4组映射点，这也是为什么我们需要提供变换前后的4个点来表示透视变换。

至此我们也可以理解为什么透视变换是二维到三维，三维又到二维的过程。变换之前的点为 $\left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ]$ ，这是三维空间上的点，但我们认知上它在二维平面上的投影是。通过矩阵变换成三维空间中的点 $\left[ \begin{array}{c} x'\\ y'\\ z'\\ \end{array} \right ]$ ，再通过除以三维中Ｚ轴的值得到三维空间的点 $\left[ \begin{array}{c} \frac{x'}{z'}\\ \frac{y'}{z'}\\ 1\\ \end{array} \right ]$ ，最后投影到二维平面得到点。整个过程就是把二维转到三维，再转映射回之前的二维空间。

透视变换的效果相当于观察者的视角发生改变时所观察到画面产生的变化。

为什么通过一个矩阵可以实现这种视角变化？具体的数学原理在网上没找到，大部分文章也只是止步于变换矩阵，对于具体原因没有深入说明，这困扰了我很长时间。

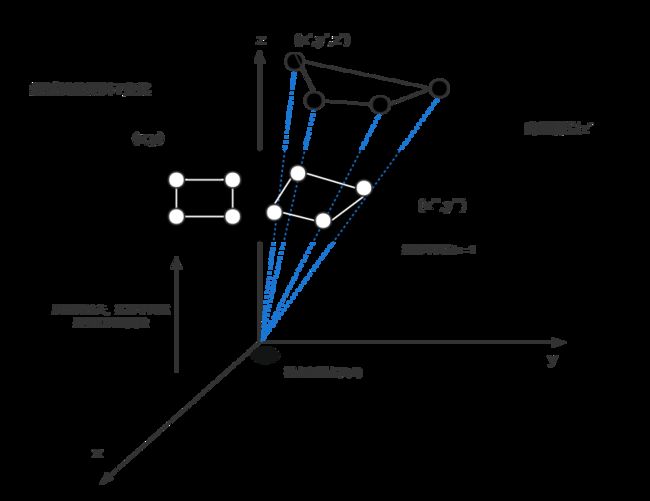
经过推证，我认为透视变换的过程应该是如下我画的图：

首先观察点位于原点，然后往z轴的正方向看去，投影面上就是我们在显示屏看到物体的位置。

经过透视变换矩阵变化，原本的变成(可以证明，变换后的点仍然处于空间中的同一个平面)。此时的坐标已经不仅仅在平面上，而是在整个三维空间中，也就是矩阵会将原本在平面内的图形转化为空间某一个平面的图形。这就是转换矩阵使得看图片的视角变化的原因。

然后该图形各个点与视点（即原点）连线，在投影面上投影形成图形。数值上的表现是三个坐标值都除以，这么做的原因其实是几何上的等比例的缩放：

$\frac{0-1}{0-z'}=\frac{0-x''}{0-x'}=\frac{0-y''}{0-y'}$

这也解决了我一直以来的困惑，即透视变换引发我们图片视角的变化并不是我们观察者视角的变化，而是观察者视角不变而对物体空间位置发生了转换，导致了我们看到的图片视角变化。这可以理解为：不是我们人走动看到了物体角度发生变化，而是人始终保持不动，其他人对物体进行了挪动导致我们看到这个物体角度发生了变化。

二、透视变换实现

在应用中，需要用到OpenCV的两个函数getPerspectiveTransform()和warpPerspective()两个函数。

1.getPerspectiveTransform()

Mat getPerspectiveTransform(InputArray src, InputArray dst, int solveMethod = DECOMP_LU)

①功能描述

从4对映射点计算透视变换的变换矩阵，返回的矩阵数据类型是Mat。这里需要注意的是，1对映射点指的是 $\left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ]$ 与 $\left[ \begin{array}{c} x''\\ y''\\ 1\\ \end{array} \right ]$ ，但是变换的矩阵作用在 $\left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ]$ 与 $\left[ \begin{array}{c} x'\\ y'\\ z'\\ \end{array} \right ]$ 。即：

$\left[ \begin{array}{c} x'\\ y'\\ z'\\ \end{array} \right ] = T \left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ]$

②参数描述

参数 src：源图像四边形的4个顶点坐标。

参数 dst：目标图像对应四边形的4个顶点坐标。

参数 solveMethod：传递给cv::solve(#DecompTypes)的计算方法，默认是DECOMP_LU，一般不用输入此参数。

返回值：Mat型变换矩阵，可直接用于warpPerspective()函数

2.warpPerspective()

void warpPerspective(
	InputArray src,
	OutputArray dst,
	InputArray M,
	Size dsize,
	int flags=INTER_LINEAR,
	int borderMode = BORDER_CONSTANT, 
	const Scalar& borderValue = Scalar())；

①功能描述

将变换矩阵应用于原图像，使其透视变换为目标图像。

②参数描述

参数src：输入图像。

参数dst：输出图像，需要初始化一个空矩阵用来保存结果，不用设定矩阵尺寸。

参数M：3x3的转换矩阵。

参数dsize：输出图像的大小。

参数flags：设置插值方法。默认为INTER_LINEAR表示双线性插值，INTER_NEAREST表示最近邻插值，WARP_INVERSE_MAP表示M作为反转转换 (dst->src) 。

参数borderMode：像素外推方法，默认为BORDER_CONSTANT，指定常数填充。翻阅官方文档发现还有一个选项是BORDER_REPLICATE。

参数borderValue：常数填充时边界的颜色设置，默认是(0,0,0)，表示黑色。这就是为什么透视变换后图片周围是黑色的原因。这里需要注意的是类型为Scalar (B, G, R)。

3.函数的使用

代码如下：

#include 
#include
using namespace std;
using namespace cv;

void main()
{
    Mat img = imread("test.png");  
    Point2f AffinePoints0[4] = { Point2f(0, 0), Point2f(img.cols, 0), Point2f(0, img.rows), Point2f(img.cols, img.rows) };//变化前的4个节点
    Point2f AffinePoints1[4] = { Point2f(100, 0), Point2f(img.cols - 100, 0),Point2f(0, img.rows), Point2f(img.cols, img.rows) };//变化后的4个节点

    Mat Trans = getPerspectiveTransform(AffinePoints0, AffinePoints1);//由4组映射点得到变换矩阵
    Mat dst_perspective;//存储目标透视图像
    warpPerspective(img, dst_perspective, Trans, Size(img.cols, img.rows));//执行透视变换

    imshow("原图像", img);
    imshow("透视变换后", dst_perspective);
    waitKey();
}

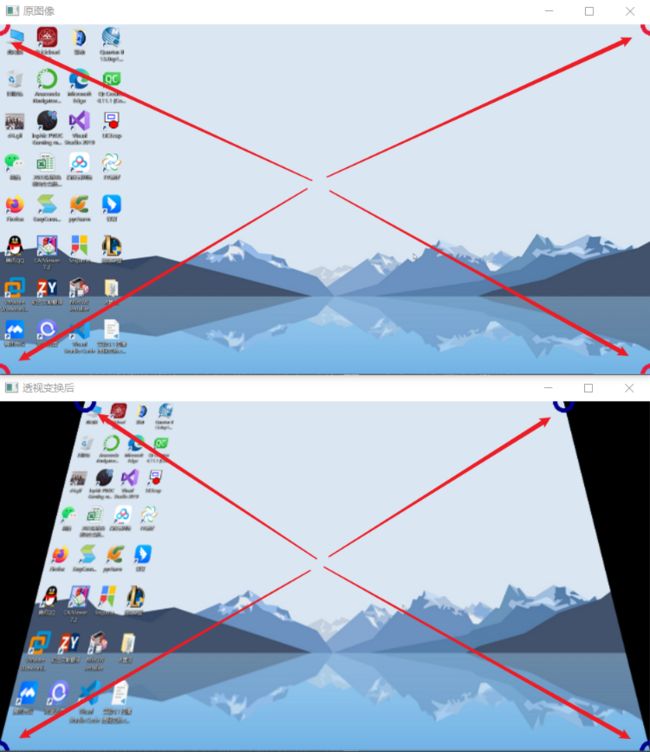
执行结果如下：

可以看到，原本的效果是从正面平视电脑屏幕，现在透视变换后是仰视电脑屏幕（或者说电脑屏幕向后倾斜）。

4.映射点标记

为了更清晰地知道变换前后的映射点，我们可以在图上标注出来，这里使用到OpenCV的circle函数。

①函数原型

void circle()

circle (
	InputOutputArray img, 
	Point center, 
	int radius, 
	const Scalar &color, 
	int thickness=1, 
	int lineType=LINE_8, 
	int shift=0)

②函数功能

在图像上画一个具有给定中心和半径的空心或实心圆。

③函数参数

参数img：画圆绘制的图像。

参数center：画圆的圆心坐标，类型为Scalar(x, y)。

参数radius：圆的半径。

参数color：圆的颜色，规则为(B,G,R)，类型为Scalar(B,G,R)。

参数thickness：如果正数表示组成圆的线条的粗细程度。如果是负数表示圆是否被填充，如FILLED表示要绘制实心的圆。

参数line_type：线条的类型，默认是LINE_8。

参数shift：圆心坐标点和半径值的小数点位数，默认为0位。

④代码过程

    for (int i = 0; i < 4; i++)//显示4组映射点的位置
    {
        //画一个圆心在映射点(转换前)，半径为10，线条粗细为3，红色的圆
        circle(img, AffinePoints0[i], 10, Scalar(59, 23, 232), 3);
        //画一个圆心在映射点(转换后)，半径为10，线条粗细为3，蓝色的圆
        circle(dst_perspective, AffinePoints1[i], 10, Scalar(139, 0, 0), 3);
    }

执行效果：

可以看到转换前后的4组点都被画了出来，因为我映射点设置在边角，所以只能看得到圆的一部分。当设置在图片中间时可以看到整个圆形。

5.库函数的实现

一般直接调用上述函数即可实现透视变换，这里为了更好的理解变换过程，我对上面两个函数中的透视变换函数进行了实现(求变换矩阵的函数就是纯数学问题，这里不再重复)，可能与官方的库函数实现有所不同。

warpPerspective的实现思路是：

已知变换矩阵和源图像，需要使用变换矩阵将源图像透视变换为目标图像。这个过程并不是我们上面理解的正向过程，即将变换矩阵T乘上原图像的所有坐标 $\left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ]$ 得到目标图像的坐标。因为这样会导致目标图像上的个别坐标 $\left[ \begin{array}{c} x''\\ y''\\ 1\\ \end{array} \right ]$ 没有映射。我们使用反向过程，将 $\left[ \begin{array}{c} x''\\ y''\\ 1\\ \end{array} \right ]$ 映射回原图像寻找目标像素值。反向映射的推导过程如下：

已知：

$\begin{equation} \left[ \begin{array}{c} x'\\ y'\\ z'\\ \end{array} \right ] = T \left[ \begin{array}{c} x\\ y\\ 1\\ \end{array} \right ] \end{equation}$

同除以：

$\begin{equation} \left[ \begin{array}{c} \frac{x'}{z'}\\ \frac{y'}{z'}\\ 1\\ \end{array} \right ] = T \left[ \begin{array}{c} \frac{x}{z'}\\ \frac{y}{z'}\\ \frac{1}{z'}\\ \end{array} \right ] \end{equation}$

同左乘 $T^{-1}$ ：

$\begin{equation} T^{-1} \left[ \begin{array}{c} \frac{x'}{z'}\\ \frac{y'}{z'}\\ 1\\ \end{array} \right ] = \left[ \begin{array}{c} \frac{x}{z'}\\ \frac{y}{z'}\\ \frac{1}{z'}\\ \end{array} \right ] \end{equation}$

即：

$\begin{equation} T^{-1} \left[ \begin{array}{c} x''\\ y''\\ 1\\ \end{array} \right ] = \left[ \begin{array}{c} \frac{x}{z'}\\ \frac{y}{z'}\\ \frac{1}{z'}\\ \end{array} \right ] \end{equation}$

设求得的变换矩阵T的逆 $T^{-1}$ 为：

$T^{-1}= \left[ \begin{array}{ccc} c_{11}& c_{12} &c_{13}\\ c_{21}& c_{22} &c_{23}\\ c_{31}& c_{32} &c_{33}\\ \end{array} \right ]$

展开后可以得到：

$\begin{equation} \left\{ \begin{matrix}{} x=(c_{11}x''+c_{12}y''+c_{13})z' \\ y=(c_{21}x''+c_{22}y''+c_{23})z'\\ z'=\frac{1}{c_{31}x''+c_{32}y''+c_{33}}\\ \end{array} \right. \end{equation}$

该式表明，当我们求得变换矩阵T的逆 $T^{-1}$ 之后，对于目标图像上的任意坐标都可以用上面公式求得在原图像上对应坐标的位置，进而得到这个位置的像素值。当然，位置不一定是整数，可能需要插值。

代码实现过程如下：

//自己实现的wrapPerspective函数
void _wrapPerspective(const Mat& src, const Mat& T, Mat& dst)//src为源图像，T为变换矩阵，dst为目标图像
{
    dst.create(src.size(), src.type());//创建一个和原图像一样大小的Mat
    Mat T_inverse;//变换矩阵的逆
    invert(T, T_inverse);//求矩阵T的逆，结果存到T_inverse
    //取出矩阵中的值
    double c11 = T_inverse.ptr(0)[0];
    double c12 = T_inverse.ptr(0)[1];
    double c13 = T_inverse.ptr(0)[2];
    double c21 = T_inverse.ptr(1)[0];
    double c22 = T_inverse.ptr(1)[1];
    double c23 = T_inverse.ptr(1)[2];
    double c31 = T_inverse.ptr(2)[0];
    double c32 = T_inverse.ptr(2)[1];
    double c33 = T_inverse.ptr(2)[2];
    //遍历目标图像的每个位置，求取原图像对应位置的像素值
    
    for (int y = 0; y < dst.rows; y++)
    {
        for (int x = 0; x < dst.cols; x++)
        {
            double xp = c11 * x + c12 * y + c13;
            double yp = c21 * x + c22 * y + c23;
            double z = c31 * x + c32 * y + c33;//z'
            z = z ? 1.0 / z : 0;//z'不为0时求导数，否则设为0
            xp *= z;
            yp *= z;
            //将双精度坐标限制在整型能表示的最大最小值之间
            double fx = max((double)INT_MIN, min((double)INT_MAX, xp));
            double fy = max((double)INT_MIN, min((double)INT_MAX, yp));
            //转化为int，这里简单地使用了最近邻插值
            int X = saturate_cast(fx);
            int Y = saturate_cast(fy);
            //是否在原图像大小范围内
            if (X >= 0 && X < src.cols && Y >= 0 && Y < src.cols)
            {
                dst.at(y, x)[0] = src.at(Y, X)[0];
                dst.at(y, x)[1] = src.at(Y, X)[1];
                dst.at(y, x)[2] = src.at(Y, X)[2];
            }
            else//以黑色填充
            {
                dst.at(y, x)[0] = 0;
                dst.at(y, x)[1] = 0;
                dst.at(y, x)[2] = 0;
            }
        }
    }
}

运行效果：

和官方的函数实现的结果比较可发现基本一致，说明实现思路正确。

三、透视变换的应用

1、透视变换的交互程序

①实验要求：

设计一个交互程序，可以编辑四边形顶点，并且顶点位置改变时图像形变的结果可以实时更新。

②实验思路：

根据上面提到的知识，实现已知4对映射点的的透视变换是很容易的。因此问题的难点在于如何设计交互程序，这里需要使用到OpenCV的鼠标点击事件。

void setMousecallback(const string& winname, MouseCallback onMouse, void* userdata=0)

参数描述：

winname：窗口的名字。

onMouse：鼠标响应函数或者说回调函数。指定窗口里每次鼠标事件发生的时候，被调用的函数指针。这个函数的原型为void on_Mouse(int event, int x, int y, int flags, void* param)。

userdata：传给回调函数的参数，默认为0。这个参数我个人还没用到过。

void MouseCallback(int event,int x,int y,int flags,void *useradata);

参数描述：

event：鼠标事件。

x：鼠标事件的x坐标。

y：鼠标事件的y坐标。

flags: 代表鼠标的拖拽事件和键盘鼠标联合的事件。

userdata : 可选的参数，目前没用到过。

鼠标事件event主要有下面几种：

EVENT_MOUSEMOVE ：鼠标移动

EVENT_LBUTTONDOWN : 鼠标左键按下

EVENT_RBUTTONDOWN : 鼠标右键按下

EVENT_MBUTTONDOWN ：鼠标中键按下

EVENT_LBUTTONUP ：鼠标左键放开

EVENT_RBUTTONUP ：鼠标右键放开

EVENT_MBUTTONUP ：中键放开

EVENT_LBUTTONDBLCLK ：左键双击

EVENT_RBUTTONDBLCLK ：右键双击

EVENT_MBUTTONDBLCLK ：中键双击

Flags主要有一下几种：

EVENT_FLAG_LBUTTON ：左键拖拽

EVENT_FLAG_RBUTTON ：右键拖拽

EVENT_FLAG_MBUTTON ：中键拖拽

EVENT_FLAG_CTRLKEY ： Ctrl按下不放

EVENT_FLAG_SHIFTKEY ： shift按下不放

EVENT_FLAG_ALTKEY ： alt按下不放

总体思路：

为了更好的观感，我们需要一张比原图像稍大一点的画布来放目标图像。初始4个映射点在原图像的4个角上。在这张画布上，当鼠标移动到4个映射点的圆形范围时，如果此时按下左键不放开就可以实现映射点的拖拽。当鼠标左键放开时，此时鼠标的位置就是映射点移动后的位置。然后重新计算变换矩阵，对原图像实现透视变换并显示。

当然实时更新也可以理解为当左键拖拽时映射点位置一发生变化就计算变换矩阵并实现透视变换，但实验中发现这样延迟很高(debug模式下)，并且实际使用中我们有时候已经明确要将映射点移动到某个目标位置了，但在这移动过程中都会进行不必要的透视变换。

③实现过程

重点在于鼠标事件的编写，其他的过程都与前面透视变换方法相似。

当左键按下时，需要判断是否点击在了映射点的区域，如果点在了有效区域，那么还需要记录点击的是哪一个映射点。

当左键按下并拖拽时，如果需要在拖拽过程中实时更新透视变换，那么实时记录映射点位置并进行透视变换。我这里实现方式上选择了左键松开后再进行透视变换，因此左键拖拽时不需要记录映射点位置。但为了更好的交互效果，我还是记录位置并绘制了一些直线和圆形进行交互提示。

当左键松开后，执行透视变换。

具体代码如下：

void mouseHander(int event, int x, int y, int flags, void* p)
{
    if (event == EVENT_LBUTTONDOWN)//左键按下
    {
        for (int i = 0; i < 4; i++)
        {
            //判断是否选择了某个映射点
            if (abs(x - dstPoint[i].x) <= radius && abs(y - dstPoint[i].y) <= radius)
            {
                pickPoint = i;
                beforePlace = dstPoint[pickPoint];//记录原本的位置
                break;
            }
        }
    }
    else if (event == EVENT_MOUSEMOVE && pickPoint >= 0 )//左键按下后选取了某个点且拖拽
    {
        //更改映射后坐标
        dstPoint[pickPoint].x = x, dstPoint[pickPoint].y = y;
        //在临时图像上实时显示鼠标拖动时形成的图像
        //注意不能直接在dstImg上画，否则会画很多次
        Mat tmp = dstImg.clone();
        //原本的圆
        circle(tmp, beforePlace, radius, Scalar(228, 164, 140), -1);
        //绘制直线
        line(tmp, dstPoint[0], dstPoint[1], Scalar(246, 230, 171), 5, 8);
        line(tmp, dstPoint[1], dstPoint[2], Scalar(246, 230, 171), 5, 8);
        line(tmp, dstPoint[2], dstPoint[3], Scalar(246, 230, 171), 5, 8);
        line(tmp, dstPoint[3], dstPoint[0], Scalar(246, 230, 171), 5, 8);
        //重新绘制4个圆
        for (int i = 0; i < 4; i++)
        {
            if (i != pickPoint)
                circle(tmp, dstPoint[i], radius, Scalar(228, 164, 140), -1);
            else
                circle(tmp, dstPoint[i], radius, Scalar(96, 96, 240), -1);
        }
        imshow("透视变换后", tmp);
    }
    else if (event == EVENT_LBUTTONUP && pickPoint >= 0)//左键松开
    {
        //执行透视变换
        Mat Trans = getPerspectiveTransform(srcPoint, dstPoint);//由4组映射点得到变换矩阵
        warpPerspective(srcImg, dstImg, Trans, Size(dstImg.cols, dstImg.rows));//执行透视变换
        for (int i = 0; i < 4; i++)//显示4组映射点的位置
        {
            //画一个圆心在映射点(转换后)，半径为10，线条粗细为3，黄色的圆
            circle(dstImg, dstPoint[i], radius, Scalar(0, 215, 255), 3);
        }
        imshow("透视变换后", dstImg);
        pickPoint = -1;//重置选取状态
    }
}

④运行结果

接着对不同图片进行测试：

可以看到对路的海报透视变换后，我们看的视角从平视变成了俯视路面。

今天随手拍了一张图书馆的照片，是从图书馆左侧的位置拍摄的，对其透视变换：

可以看到调整完后，视角更接近于正面。

⑤源代码

#include 
#include
using namespace std;
using namespace cv;

Mat srcImg, dstImg;//原图像、目标图像
Point2f srcPoint[4], dstPoint[4];//原图像和目标图像的4个映射点
Point2f beforePlace;//记录移动映射点之前的位置
int radius;//映射点的判定半径
int pickPoint;//记录点击了哪个点

void mouseHander(int event, int x, int y, int flags, void* p)
{
    if (event == EVENT_LBUTTONDOWN)//左键按下
    {
        for (int i = 0; i < 4; i++)
        {
            //判断是否选择了某个映射点
            if (abs(x - dstPoint[i].x) <= radius && abs(y - dstPoint[i].y) <= radius)
            {
                pickPoint = i;
                beforePlace = dstPoint[pickPoint];//记录原本的位置
                break;
            }
        }
    }
    else if (event == EVENT_MOUSEMOVE && pickPoint >= 0 )//左键按下后选取了某个点且拖拽
    {
        //更改映射后坐标
        dstPoint[pickPoint].x = x, dstPoint[pickPoint].y = y;
        //在临时图像上实时显示鼠标拖动时形成的图像
        //注意不能直接在dstImg上画，否则会画很多次
        Mat tmp = dstImg.clone();
        //原本的圆
        circle(tmp, beforePlace, radius, Scalar(228, 164, 140), -1);
        //绘制直线
        line(tmp, dstPoint[0], dstPoint[1], Scalar(246, 230, 171), 5, 8);
        line(tmp, dstPoint[1], dstPoint[2], Scalar(246, 230, 171), 5, 8);
        line(tmp, dstPoint[2], dstPoint[3], Scalar(246, 230, 171), 5, 8);
        line(tmp, dstPoint[3], dstPoint[0], Scalar(246, 230, 171), 5, 8);
        //重新绘制4个圆
        for (int i = 0; i < 4; i++)
        {
            if (i != pickPoint)
                circle(tmp, dstPoint[i], radius, Scalar(228, 164, 140), -1);
            else
                circle(tmp, dstPoint[i], radius, Scalar(96, 96, 240), -1);
        }
        imshow("透视变换后", tmp);
    }
    else if (event == EVENT_LBUTTONUP && pickPoint >= 0)//左键松开
    {
        //执行透视变换
        Mat Trans = getPerspectiveTransform(srcPoint, dstPoint);//由4组映射点得到变换矩阵
        warpPerspective(srcImg, dstImg, Trans, Size(dstImg.cols, dstImg.rows));//执行透视变换
        for (int i = 0; i < 4; i++)//显示4组映射点的位置
        {
            //画一个圆心在映射点(转换后)，半径为10，线条粗细为3，黄色的圆
            circle(dstImg, dstPoint[i], radius, Scalar(0, 215, 255), 3);
        }
        imshow("透视变换后", dstImg);
        pickPoint = -1;//重置选取状态
    }
}

void main()
{
    srcImg = imread("library.jpg");  
    radius = 10;//设置四个点的圆的半径
    pickPoint = -1;
    //映射前的4个点
    srcPoint[0] = Point2f(0, 0);
    srcPoint[1] = Point2f(srcImg.cols, 0);
    srcPoint[2] = Point2f(srcImg.cols, srcImg.rows);
    srcPoint[3] = Point2f(0, srcImg.rows);
    //创建一张略大于原图像的画布
    dstImg = Mat::zeros(Size(2 * radius + 100 + srcImg.cols, 2 * radius + 100 + srcImg.rows), srcImg.type());
    //初始映射后的4个点
    dstPoint[0] = Point2f(radius + 50, radius + 50);
    dstPoint[1] = Point2f(radius + 50 + srcImg.cols, radius + 50);
    dstPoint[2] = Point2f(radius + 50 + srcImg.cols, radius + 50 + srcImg.rows);
    dstPoint[3] = Point2f(radius + 50, radius + 50 + srcImg.rows);
    Mat Trans = getPerspectiveTransform(srcPoint, dstPoint);//由4组映射点得到变换矩阵
    Mat dst_perspective;//存储目标透视图像
    warpPerspective(srcImg, dstImg, Trans, Size(dstImg.cols, dstImg.rows));//执行透视变换

    for (int i = 0; i < 4; i++)//显示初始4组映射点的位置
    {
        //画一个圆心在映射点(转换后)，半径为10，线条粗细为3，黄色的圆
        circle(dstImg, dstPoint[i], radius, Scalar(95, 180, 243), 3);
    }
    imshow("原图像", srcImg);
    imshow("透视变换后", dstImg);
    //鼠标事件
    setMouseCallback("透视变换后", mouseHander);
    waitKey();
}

2.虚拟广告牌的实现

根据上面的透视变换的过程，我们可以想到一种应用：将图片A作为广告牌透视变换到图片B的特定位置。

实现过程也很容易，我们将图片A的初始映射点设置在四个角上，然后在背景图B上选择透视变换后的4个映射点，然后将图片A透视变换到指定位置（将图片B的原位置覆盖）。这里需要注意的是映射点的选取需要规定好固定的顺序，否则无法与原本的映射点一一对应，我默认选取点的顺序是从左上角开始顺时针选取。

#include 
#include
using namespace std;
using namespace cv;

Mat srcImg, dstImg;//原图像、目标图像
Mat resultImg;//结果图像
vector srcPoints, dstPoints;//原图像和目标图像的映射点
int pickNums;//目前已选取的节点

void mouseHander(int event, int x, int y, int flags, void* p)
{
    if (event == EVENT_LBUTTONDOWN)//左键按下
    {
        Mat tmp = dstImg.clone();
        if (pickNums == 4)//选取的点超过4个后，下一次点击会实现透视变换
        {
            //执行透视变换
            Mat Trans = getPerspectiveTransform(srcPoints, dstPoints);//由4组映射点得到变换矩阵
            warpPerspective(srcImg, tmp, Trans, Size(tmp.cols, tmp.rows));//执行透视变换
            resultImg = dstImg.clone();
            for (int y = 0; y < dstImg.rows; y++)
            {
                for (int x = 0; x < dstImg.cols; x++)
                {
                    if ((int)tmp.at(y, x)[0] == 0 && (int)tmp.at(y, x)[1] == 0 && (int)tmp.at(y, x)[2] == 0)//像素点全0
                        continue;
                    else//非全0
                    {
                        resultImg.at(y, x)[0] = tmp.at(y, x)[0];
                        resultImg.at(y, x)[1] = tmp.at(y, x)[1];
                        resultImg.at(y, x)[2] = tmp.at(y, x)[2];
                    }
                }
            }
            imshow("虚拟广告牌", resultImg);
            dstPoints.clear();
            pickNums = 0;
        }
        else//选取的节点还没4个
        {
            dstPoints.push_back(Point2f(x, y));
            pickNums++;
            for (int i = 0; i < dstPoints.size(); i++)
            {
                circle(tmp, dstPoints[i], 5, Scalar(0, 215, 255), 3);
            }
            imshow("虚拟广告牌", tmp);
        }
    }

}

int main()
{
    srcImg = imread("test.png");//透视变换的图像，也就是广告图

    //设置原图像的4个映射点
    srcPoints.push_back(Point2f(0, 0));
    srcPoints.push_back(Point2f(srcImg.cols, 0));
    srcPoints.push_back(Point2f(srcImg.cols, srcImg.rows));
    srcPoints.push_back(Point2f(0, srcImg.rows));

    dstImg = imread("library.jpg");//背景图

    imshow("虚拟广告牌", dstImg);
    //鼠标事件
    setMouseCallback("虚拟广告牌", mouseHander);
    waitKey(0);
    return 0;
}

实现效果：

我们还可以用来把同学的电脑屏幕变成你想要的照片：

你可能感兴趣的:(opencv,计算机视觉,图像处理,c++)

c++ 的iostream 和 c++的stdio的区别和联系黄卷青灯77 c++算法开发语言 iostream stdio
在C++中，iostream和C语言的stdio.h都是用于处理输入输出的库，但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系：区别1.编程风格iostream（C++风格）：C++标准库中的输入输出流类库，支持面向对象的输入输出操作。典型用法是cin（输入）和cout（输出），使用>操作符来处理数据。更加类型安全，支持用户自定义类型的输入输出。#includeintmain(){in
Linux下QT开发的动态库界面弹出操作（SDL2） 13jjyao QT类 qt 开发语言 sdl2 linux
需求：操作系统为linux，开发框架为qt，做成需带界面的qt动态库，调用方为java等非qt程序难点：调用方为java等非qt程序，也就是说调用方肯定不带QApplication::exec()，缺少了这个，QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出)；这与qt调用本身qt库是有本质的区别的思路：1.调用方缺QApplication::exec()，那么我们在接口
【JS】执行时长(100分) |思路参考+代码解析（C++） l939035548 JS 算法数据结构 c++
题目为了充分发挥GPU算力，需要尽可能多的将任务交给GPU执行，现在有一个任务数组，数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。假设GPU最多一次执行n个任务，一次执行耗时1秒，在保证GPU不空闲情况下，最少需要多长时间执行完成。题目输入第一个参数为GPU一次最多执行的任务个数，取值范围[1,10000]第二个参数为任务数组长度，取值范围[1,10000]第三个参数为任务数组，数字范围
基于CODESYS的多轴运动控制程序框架：逻辑与运动控制分离，快速开发灵活操作 GPJnCrbBdl python 开发语言
基于codesys开发的多轴运动控制程序框架，将逻辑与运动控制分离，将单轴控制封装成功能块，对该功能块的操作包含了所有的单轴控制（归零、点动、相对定位、绝对定位、设置当前位置、伺服模式切换等等）。程序框架由主程序按照状态调用分归零模式、手动模式、自动模式、故障模式，程序状态的跳转都已完成，只需要根据不同的工艺要求完成所需的动作即可。变量的声明、地址的规划都严格按照C++的标准定义，能帮助开发者快速
C++ | Leetcode C++题解之第409题最长回文串 Ddddddd_158 经验分享 C++Leetcode 题解
题目：题解：classSolution{public:intlongestPalindrome(strings){unordered_mapcount;intans=0;for(charc:s)++count[c];for(autop:count){intv=p.second;ans+=v/2*2;if(v%2==1andans%2==0)++ans;}returnans;}};
C++菜鸟教程 - 从入门到精通第二节 DreamByte c++
一.上节课的补充(数据类型)1.前言继上节课,我们主要讲解了输入,输出和运算符,我们现在来补充一下数据类型的知识上节课遗漏了这个知识点,非常的抱歉顺便说一下,博主要上高中了,更新会慢,2-4周更新一次对了,正好赶上中秋节,小编跟大家说一句:中秋节快乐!2.int类型上节课,我们其实只用了int类型int类型,是整数类型,它们存贮的是整数,不能存小数(浮点数)定义变量的方式很简单inta;//定义一
Java面试题精选：消息队列(二) 芒果不是芒 Java面试题精选 java kafka
一、Kafka的特性1.消息持久化：消息存储在磁盘，所以消息不会丢失2.高吞吐量：可以轻松实现单机百万级别的并发3.扩展性：扩展性强，还是动态扩展4.多客户端支持：支持多种语言（Java、C、C++、GO、）5.KafkaStreams（一个天生的流处理）:在双十一或者销售大屏就会用到这种流处理。使用KafkaStreams可以快速的把销售额统计出来6.安全机制：Kafka进行生产或者消费的时候会
C++ lambda闭包消除类成员变量 barbyQAQ c++c++java 算法
原文链接：https://blog.csdn.net/qq_51470638/article/details/142151502一、背景在面向对象编程时，常常要添加类成员变量。然而类成员一旦多了之后，也会带来干扰。拿到一个类，一看成员变量好几十个，就问你怕不怕？二、解决思路可以借助函数式编程思想，来消除一些不必要的类成员变量。三、实例举个例子：classClassA{public:...intfu
tiff批量转png 诺有缸的高飞鸟 opencv 图像处理 python opencv 图像处理
目录写在前面代码完写在前面1、本文内容tiff批量转png2、平台/环境opencv,python3、转载请注明出处：https://blog.csdn.net/qq_41102371/article/details/132975023代码importnumpyasnpimportcv2importosdeffindAllFile(base):file_list=[]forroot,ds,fsin
2021 CCF 非专业级别软件能力认证第一轮（CSP-J1）入门级C++语言试题（第三大题：完善程序代码） mmz1207 c++csp
最近有一段时间没更新了，在准备CSP考试，请大家见谅。（1）有n个人围成一个圈，依次标号0到n-1。从0号开始，依次0，1，0，1...交替报数，报到一的人离开，直至圈中剩最后一个人。求最后剩下的人的编号。#includeusingnamespacestd;intf[1000010];intmain(){intn;cin>>n;inti=0,cnt=0,p=0;while(cnt#includeu
《 C++ 修炼全景指南：九》打破编程瓶颈！掌握二叉搜索树的高效实现与技巧 Lenyiin C++修炼全景指南技术指南 c++算法 stl
摘要本文详细探讨了二叉搜索树（BinarySearchTree,BST）的核心概念和技术细节，包括插入、查找、删除、遍历等基本操作，并结合实际代码演示了如何实现这些功能。文章深入分析了二叉搜索树的性能优势及其时间复杂度，同时介绍了前驱、后继的查找方法等高级功能。通过自定义实现的二叉搜索树类，读者能够掌握其实际应用，此外，文章还建议进一步扩展为平衡树（如AVL树、红黑树）以优化极端情况下的性能退化。
遥感影像的切片处理 sand&wich 计算机视觉 python 图像处理
在遥感影像分析中，经常需要将大尺寸的影像切分成小片段，以便于进行详细的分析和处理。这种方法特别适用于机器学习和图像处理任务，如对象检测、图像分类等。以下是如何使用Python和OpenCV库来实现这一过程，同时确保每个影像片段保留正确的地理信息。准备环境首先，确保安装了必要的Python库，包括numpy、opencv-python和xml.etree.ElementTree。这些库将用于图像处理
Python实现下载当前年份的谷歌影像 sand&wich python 开发语言
在GIS项目和地图应用中，获取最新的地理影像数据是非常重要的。本文将介绍如何使用Python代码从Google地图自动下载当前年份的影像数据，并将其保存为高分辨率的TIFF格式文件。这个过程涉及地理坐标转换、多线程下载和图像处理。关键功能该脚本的核心功能包括：坐标转换：支持WGS-84与WebMercator投影之间转换，以及处理中国GCJ-02偏移。自动化下载：多线程下载地图瓦片，提高效率。图像
20个新手学习c++必会的程序输出*三角形、杨辉三角等（附代码） X_StarX c++学习算法大学生开发语言数据结构
示例1:HelloWorld#includeusingnamespacestd;intmain(){coutusingnamespacestd;intmain(){inta=5;intb=10;intsum=a+b;coutusingnamespacestd;intfactorial(intn){if(nusingnamespacestd;voidprintFibonacci(intn){intt
C++八股 Petrichorzncu 八股总结 c++开发语言
这里写目录标题C++内存管理C++的构造函数，复制构造函数，和析构函数深复制与浅复制：构造函数和析构函数哪个能写成虚函数，为什么？C++数据结构内存排列结构体和类占用的内存：==虚函数和虚表的原理==虚函数虚表（Vtable）虚函数和虚表的实现细节==内存泄漏==指针的工作原理函数的传值和传址new和delete与malloc和freeC++内存区域划分C++11新特性C++常见新特性==智能指针
【2022 CCF 非专业级别软件能力认证第一轮（CSP-J1）入门级 C++语言试题及解析】汉子萌萌哒 CCF noi 算法数据结构 c++
一、单项选择题(共15题，每题2分，共计30分；每题有且仅有一个正确选项)1.以下哪种功能没有涉及C++语言的面向对象特性支持：()。A.C++中调用printf函数B.C++中调用用户定义的类成员函数C.C++中构造一个class或structD.C++中构造来源于同一基类的多个派生类题目解析【解析】正确答案:AC++基础知识，面向对象和类有关，类又涉及父类、子类、继承、派生等关系，printf
《 C++ 修炼全景指南：十》自平衡的艺术：深入了解 AVL 树的核心原理与实现 Lenyiin C++修炼全景指南技术指南 c++数据结构 stl
摘要本文深入探讨了AVL树（自平衡二叉搜索树）的概念、特点以及实现细节。我们首先介绍了AVL树的基本原理，并详细分析了其四种旋转操作，包括左旋、右旋、左右双旋和右左双旋，阐述了它们在保持树平衡中的重要作用。接着，本文从头到尾详细描述了AVL树的插入、删除和查找操作，配合完整的代码实现和详尽的注释，使读者能够全面理解这些操作的执行过程。此外，我们还提供了AVL树的遍历方法，包括中序、前序和后序遍历，
Python实现TIFF 文件转换为 PNG 和 JPG 格式 sand&wich python 开发语言
在日常的图像处理工作中，可能会遇到需要将TIFF格式的图像转换为其他格式的情况，例如PNG和JPG。下面，本文将介绍如何使用Python和GDAL库实现这一功能。准备工作在开始之前，请确保已经安装了必要的库：GDAL（GeospatialDataAbstractionLibrary）可以使用以下命令安装GDAL：pipinstallgdal代码实现以下是一个将TIFF文件转换为PNG文件的示例代码
JAVA学习笔记之23种设计模式学习 victorfreedom Java技术设计模式 android java 常用设计模式
博主最近买了《设计模式》这本书来学习，无奈这本书是以C++语言为基础进行说明，整个学习流程下来效率不是很高，虽然有的设计模式通俗易懂，但感觉还是没有充分的掌握了所有的设计模式。于是博主百度了一番，发现有大神写过了这方面的问题，于是博主迅速拿来学习。一、设计模式的分类总体来说设计模式分为三大类：创建型模式，共五种：工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。结构型模式，共七种：适配器
windows下python opencv ffmpeg读取摄像头实现rtsp推流拉流图像处理大大大大大牛啊 opencv实战代码讲解视觉图像项目 windows python opencv
windows下pythonopencvffmpeg读取摄像头实现rtsp推流拉流整体流程1.下载所需文件1.1下载rtsp推流服务器1.2下载ffmpeg2.开启RTSP服务器3.opencv读取摄像头并调用ffmpeg进行推流4.opencv进行拉流5.opencv异步拉流整体流程1.下载所需文件1.1下载rtsp推流服务器下载RTSP服务器下载页面https://github.com/blu
c++ opencv4.3 sift匹配图像处理大大大大大牛啊图像处理 opencv实战代码讲解 opencv sift c++opencv4 特征点
c++opencv4.3sift匹配main.cppintmain(){vectorkeypoints1,keypoints2;Matimg1,img2,descriptors1,descriptors2;intnumF
《 C++ 修炼全景指南：四》揭秘 C++ List 容器背后的实现原理，带你构建自己的双向链表 Lenyiin 技术指南 C++修炼全景指南 c++list 链表 stl
本篇博客，我们将详细讲解如何从头实现一个功能齐全且强大的C++List容器，并深入到各个细节。这篇博客将包括每一步的代码实现、解释以及扩展功能的探讨，目标是让初学者也能轻松理解。一、简介1.1、背景介绍在C++中，std::list是一个基于双向链表的容器，允许高效的插入和删除操作，适用于频繁插入和删除操作的场景。与动态数组不同，list允许常数时间内的插入和删除操作，支持双向遍历。这篇文章将详细
AI大模型的架构演进与最新发展季风泯灭的季节 AI大模型应用技术二人工智能架构
随着深度学习的发展，AI大模型（LargeLanguageModels,LLMs）在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进，包括从Transformer的提出到GPT、BERT、T5等模型的历史演变，并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍：Transformer的核心原理Transformer架构的背景在Transfo
c++ 内存处理函数 heeheeai c++开发语言
在C语言的头文件中，memcpy和memmove函数都用于复制内存块，但它们在处理内存重叠方面存在关键区别：内存重叠:memcpy函数不保证在源内存和目标内存区域重叠时能够正确复制数据。如果内存区域重叠，memcpy的行为是未定义的，可能会导致数据损坏或程序崩溃。memmove函数能够安全地处理源内存和目标内存区域重叠的情况。它会确保在复制过程中不会覆盖尚未复制的数据，从而保证数据的完整性。效率:
【c++基础概念深度理解——堆和栈的区别，并实现堆溢出和栈溢出】 XWWW668899 C++基本概念 c++c语言开发语言青少年编程
文章目录概要技术名词解释栈溢出和堆溢出小结概要学习C++语言，避免不了要好好理解一下堆（Heap）和栈（Stack），有助于更好地管理内存，以及如何写出一段程序“成功实现”堆溢出和栈溢出。技术名词解释理解东西最快的方式是根据自己目前能理解的词语去关联新的概念，不断的纠正，向正确的深度理解靠近，当无限接近的时候也就理解了想要理解的概念。我们经常说堆栈，把这两个名词放到一起。其实，堆是堆，栈是栈，两种
C++常见知识掌握 nfgo c++开发语言
1.Linux软件开发、调试与维护内核与系统结构Linux内核是操作系统的核心，负责管理硬件资源，提供系统服务，它是系统软件与硬件之间的桥梁。主要组成部分包括：进程管理：内核通过调度器分配CPU时间给各个进程，实现进程的创建、调度、终止等操作。使用进程描述符（task_struct）来存储进程信息，包括状态（就绪、运行、阻塞等）、优先级、内存映射等。内存管理：包括物理内存和虚拟内存管理。通过页表映
metaRTC5.0 API编程指南(一) metaRTC metaRTC c++c语言 webrtc
概述metaRTC5.0版本API进行了重构，本篇文章将介绍webrtc传输调用流程和例子。metaRTC5.0版本提供了C++和纯C两种接口。纯C接口YangPeerConnection头文件:include/yangrtc/YangPeerConnection.htypedefstruct{void*conn;YangAVInfo*avinfo;YangStreamConfigstreamco
sublime个人设置 bawangtianzun sublime text 编辑器
如何拥有jiangly蒋老师同款编译器(sublimec++配置竞赛向）_哔哩哔哩_bilibiliSublimeText4的安装教程（新手竞赛向）-知乎(zhihu.com)创建文件自动保存为c++打开SublimeText软件。转到"Tools"（工具）>"Developer"（开发者）>"NewPlugin"（新建插件）。在打开的新文件中，粘贴以下代码：importsublimeimport
ubuntu安装opencv最快的方法 Derek重名了
最快方法，当然不能太多文字$sudoapt-getinstallpython-opencv借助python就可以把ubuntu的opencv环境搞起来，非常快非常容易参考：https://docs.opencv.org/trunk/d2/de6/tutorial_py_setup_in_ubuntu.html
Rust是否会取代C/C++？Rust与C/C++的较量 AI与编程之窗源码编译与开发 rust c语言 c++内存安全并发编程代码安全性能优化
目录引言第一部分：Rust语言的优势内存安全性并发性性能社区和生态系统的成长第二部分：C/C++语言的优势和地位历史积淀和成熟度广泛的库和工具支持性能优化和硬件控制丰富的行业应用社区和行业支持第三部分：挑战和阻碍学习曲线现有代码库的迁移成本生态系统和工具链的完善度社区和人才培养行业应用和推广法规和标准化第四部分：未来趋势和可能性行业趋势教育和人才培养兼容和共存行业标准化企业支持和应用开源社区和生态
iOS http封装 374016526 ios 服务器交互 http 网络请求
程序开发避免不了与服务器的交互，这里打包了一个自己写的http交互库。希望可以帮到大家。内置一个basehttp，当我们创建自己的service可以继承实现。 KuroAppBaseHttp *baseHttp = [[KuroAppBaseHttp alloc] init]; [baseHttp setDelegate:self]; [baseHttp
lolcat ：一个在 Linux 终端中输出彩虹特效的命令行工具 brotherlamp linux linux教程 linux视频 linux自学 linux资料
那些相信 Linux 命令行是单调无聊且没有任何乐趣的人们，你们错了，这里有一些有关 Linux 的文章，它们展示着 Linux 是如何的有趣和“淘气” 。在本文中，我将讨论一个名为“lolcat”的小工具 – 它可以在终端中生成彩虹般的颜色。何为 lolcat ? Lolcat 是一个针对 Linux，BSD 和 OSX 平台的工具，它类似于 cat 命令，并为 cat
MongoDB索引管理（1）——[九] eksliang mongodb MongoDB管理索引
转载请出自出处：http://eksliang.iteye.com/blog/2178427 一、概述数据库的索引与书籍的索引类似，有了索引就不需要翻转整本书。数据库的索引跟这个原理一样，首先在索引中找，在索引中找到条目以后，就可以直接跳转到目标文档的位置，从而使查询速度提高几个数据量级。不使用索引的查询称
Informatica参数及变量 18289753290 Informatica 参数变量
下面是本人通俗的理解，如有不对之处，希望指正 info参数的设置：在info中用到的参数都在server的专门的配置文件中（最好以parma）结尾下面的GLOBAl就是全局的，$开头的是系统级变量，$$开头的变量是自定义变量。如果是在session中或者mapping中用到的变量就是局部变量，那就把global换成对应的session或者mapping名字。 [GLOBAL] $Par
python 解析unicode字符串为utf8编码字符串酷的飞上天空 unicode
php返回的json字符串如果包含中文，则会被转换成\uxx格式的unicode编码字符串返回。在浏览器中能正常识别这种编码，但是后台程序却不能识别，直接输出显示的是\uxx的字符，并未进行转码。转换方式如下 >>> import json >>> q = '{"text":"\u4
Hibernate的总结永夜-极光 Hibernate
1.hibernate的作用,简化对数据库的编码,使开发人员不必再与复杂的sql语句打交道做项目大部分都需要用JAVA来链接数据库，比如你要做一个会员注册的页面，那么获取到用户填写的基本信后，你要把这些基本信息存入数据库对应的表中，不用hibernate还有mybatis之类的框架，都不用的话就得用JDBC，也就是JAVA自己的，用这个东西你要写很多的代码，比如保存注册信
SyntaxError: Non-UTF-8 code starting with '\xc4' 随便小屋 python
刚开始看一下Python语言，传说听强大的，但我感觉还是没Java强吧！写Hello World的时候就遇到一个问题，在Eclipse中写的，代码如下 ''' Created on 2014年10月27日 @author: Logic ''' print("Hello World!"); 运行结果 SyntaxError: Non-UTF-8
学会敬酒礼仪不做酒席菜鸟 aijuans 菜鸟
俗话说，酒是越喝越厚，但在酒桌上也有很多学问讲究，以下总结了一些酒桌上的你不得不注意的小细节。细节一：领导相互喝完才轮到自己敬酒。敬酒一定要站起来，双手举杯。细节二：可以多人敬一人，决不可一人敬多人，除非你是领导。细节三：自己敬别人，如果不碰杯，自己喝多少可视乎情况而定，比如对方酒量，对方喝酒态度，切不可比对方喝得少，要知道是自己敬人。细节四：自己敬别人，如果碰杯，一
《创新者的基因》读书笔记 aoyouzi 读书笔记《创新者的基因》
创新者的基因创新者的“基因”，即最具创意的企业家具备的五种“发现技能”：联想，观察，实验，发问，建立人脉。第一部分破坏性创新，从你开始第一章破坏性创新者的基因如何获得启示：发现以下的因素起到了催化剂的作用：(1) -个挑战现状的问题；(2)对某项技术、某个公司或顾客的观察；(3) -次尝试新鲜事物的经验或实验；(4)与某人进行了一次交谈，为他点醒
表单验证技术百合不是茶 JavaScript DOM对象 String对象事件
js最主要的功能就是验证表单,下面是我对表单验证的一些理解,贴出来与大家交流交流 ,数显我们要知道表单验证需要的技术点, String对象,事件,函数一:String对象;通常是对字符串的操作; 1,String的属性; 字符串.length;表示该字符串的长度; var str= "java"
web.xml配置详解之context-param bijian1013 java servlet web.xml context-param
一.格式定义： <context-param> <param-name>contextConfigLocation</param-name> <param-value>contextConfigLocationValue></param-value> </context-param> 作用：该元
Web系统常见编码漏洞（开发工程师知晓） Bill_chen sql PHP Web fckeditor 脚本
1.头号大敌：SQL Injection 原因：程序中对用户输入检查不严格，用户可以提交一段数据库查询代码，根据程序返回的结果，获得某些他想得知的数据，这就是所谓的SQL Injection，即SQL注入。本质: 对于输入检查不充分，导致SQL语句将用户提交的非法数据当作语句的一部分来执行。示例： String query = "SELECT id FROM users
【MongoDB学习笔记六】MongoDB修改器 bit1129 mongodb
本文首先介绍下MongoDB的基本的增删改查操作，然后，详细介绍MongoDB提供的修改器，以完成各种各样的文档更新操作 MongoDB的主要操作 show dbs 显示当前用户能看到哪些数据库 use foobar 将数据库切换到foobar show collections 显示当前数据库有哪些集合 db.people.update，update不带参数，可
提高职业素养，做好人生规划白糖_ 人生
培训讲师是成都著名的企业培训讲师，他在讲课中提出的一些观点很新颖，在此我收录了一些分享一下。注：讲师的观点不代表本人的观点，这些东西大家自己揣摩。 1、什么是职业规划：职业规划并不完全代表你到什么阶段要当什么官要拿多少钱，这些都只是梦想。职业规划是清楚的认识自己现在缺什么，这个阶段该学习什么，下个阶段缺什么，又应该怎么去规划学习，这样才算是规划。
国外的网站你都到哪边看？ bozch 技术网站国外
学习软件开发技术，如果没有什么英文基础，最好还是看国内的一些技术网站，例如：开源OSchina，csdn，iteye,51cto等等。个人感觉如果英语基础能力不错的话，可以浏览国外的网站来进行软件技术基础的学习，例如java开发中常用的到的网站有apache.org 里面有apache的很多Projects,springframework.org是spring相关的项目网站,还有几个感觉不错的
编程之美-光影切割问题 bylijinnan 编程之美
package a; public class DisorderCount { /**《编程之美》“光影切割问题” * 主要是两个问题： * 1.数学公式（设定没有三条以上的直线交于同一点）： * 两条直线最多一个交点，将平面分成了4个区域； * 三条直线最多三个交点，将平面分成了7个区域； * 可以推出：N条直线 M个交点，区域数为N+M+1。
关于Web跨站执行脚本概念 chenbowen00 Web 安全跨站执行脚本
跨站脚本攻击(XSS)是web应用程序中最危险和最常见的安全漏洞之一。安全研究人员发现这个漏洞在最受欢迎的网站,包括谷歌、Facebook、亚马逊、PayPal,和许多其他网站。如果你看看bug赏金计划,大多数报告的问题属于 XSS。为了防止跨站脚本攻击,浏览器也有自己的过滤器,但安全研究人员总是想方设法绕过这些过滤器。这个漏洞是通常用于执行cookie窃取、恶意软件传播,会话劫持,恶意重定向。在
[开源项目与投资]投资开源项目之前需要统计该项目已有的用户数 comsci 开源项目
现在国内和国外,特别是美国那边,突然出现很多开源项目,但是这些项目的用户有多少,有多少忠诚的粉丝,对于投资者来讲,完全是一个未知数,那么要投资开源项目,我们投资者必须准确无误的知道该项目的全部情况,包括项目发起人的情况,项目的维持时间..项目的技术水平,项目的参与者的势力,项目投入产出的效益.....
oracle alert log file（告警日志文件） daizj oracle 告警日志文件 alert log file
The alert log is a chronological log of messages and errors, and includes the following items: All internal errors (ORA-00600), block corruption errors (ORA-01578), and deadlock errors (ORA-00060)
关于 CAS SSO 文章声明 denger SSO
由于几年前写了几篇 CAS 系列的文章，之后陆续有人参照文章去实现，可都遇到了各种问题，同时经常或多或少的收到不少人的求助。现在这时特此说明几点： 1. 那些文章发表于好几年前了，CAS 已经更新几个很多版本了，由于近年已经没有做该领域方面的事情，所有文章也没有持续更新。 2. 文章只是提供思路，尽管 CAS 版本已经发生变化，但原理和流程仍然一致。最重要的是明白原理，然后
初二上学期难记单词 dcj3sjt126com english word
lesson 课 traffic 交通 matter 要紧；事物 happy 快乐的，幸福的 second 第二的 idea 主意；想法；意见 mean 意味着 important 重要的，重大的 never 从来，决不 afraid 害怕的 fifth 第五的 hometown 故乡，家乡 discuss 讨论；议论 east 东方的 agree 同意；赞成 bo
uicollectionview 纯代码布局, 添加头部视图 dcj3sjt126com Collection
#import <UIKit/UIKit.h> @interface myHeadView : UICollectionReusableView { UILabel *TitleLable; } -(void)setTextTitle; @end #import "myHeadView.h" @implementation m
N 位随机数字串的 JAVA 生成实现 FX夜归人 java Math 随机数 Random
/** * 功能描述随机数工具类<br /> * @author FengXueYeGuiRen * 创建时间 2014-7-25<br /> */ public class RandomUtil { // 随机数生成器 private static java.util.Random random = new java.util.R
Ehcache（09）——缓存Web页面 234390216 ehcache 页面缓存
页面缓存目录 1 SimplePageCachingFilter 1.1 calculateKey 1.2 可配置的初始化参数 1.2.1 cach
spring中少用的注解@primary解析 jackyrong primary
这次看下spring中少见的注解@primary注解，例子 @Component public class MetalSinger implements Singer{ @Override public String sing(String lyrics) { return "I am singing with DIO voice
Java几款性能分析工具的对比 lbwahoo java
Java几款性能分析工具的对比摘自：http://my.oschina.net/liux/blog/51800 在给客户的应用程序维护的过程中，我注意到在高负载下的一些性能问题。理论上，增加对应用程序的负载会使性能等比率的下降。然而，我认为性能下降的比率远远高于负载的增加。我也发现，性能可以通过改变应用程序的逻辑来提升，甚至达到极限。为了更详细的了解这一点，我们需要做一些性能
JVM参数配置大全 nickys jvm 应用服务器
JVM参数配置大全 /usr/local/jdk/bin/java -Dresin.home=/usr/local/resin -server -Xms1800M -Xmx1800M -Xmn300M -Xss512K -XX:PermSize=300M -XX:MaxPermSize=300M -XX:SurvivorRatio=8 -XX:MaxTenuringThreshold=5 -
搭建 CentOS 6 服务器(14) - squid、Varnish rensanning varnish
（一）squid 安装 # yum install httpd-tools -y # htpasswd -c -b /etc/squid/passwords squiduser 123456 # yum install squid -y 设置 # cp /etc/squid/squid.conf /etc/squid/squid.conf.bak # vi /etc/
Spring缓存注解@Cache使用 tom_seed spring
参考资料 http://www.ibm.com/developerworks/cn/opensource/os-cn-spring-cache/ http://swiftlet.net/archives/774 缓存注解有以下三个： @Cacheable @CacheEvict @CachePut
dom4j解析XML时出现"java.lang.noclassdeffounderror: org/jaxen/jaxenexception"错误 xp9802
java.lang.NoClassDefFoundError: org/jaxen/JaxenExc 关键字: java.lang.noclassdeffounderror: org/jaxen/jaxenexception 使用dom4j解析XML时，要快速获取某个节点的数据，使用XPath是个不错的方法，dom4j的快速手册里也建议使用这种方式执行时却抛出以下异常： Exceptio