单目标应用:瞪羚优化算法GOA求解旅行商问题TSP(提供Matlab代码)
一、瞪羚优化算法
瞪羚优化算法(Gazelle Optimization Algorithm,GOA)由Agushaka等人于2022年提出,该算法模拟了瞪羚逃避捕食者的行为,思路新颖,性能高效。
瞪羚的身高60-110厘米,体重13-29千克。该属物种有像小鹿一样的浅棕色皮毛,身体的下部一般是白色的。然而,有些个体在背部和腹部的相邻部分有一个长长的黑色标记。雄性瞪羚有长而弯曲的角。瞪羚体质强壮,是非常敏捷的动物;脚上有4趾,但侧趾比鹿类更加退化,有适合长跑的腿,适于奔跑。可以以每小时50公里的速度持续奔跑。
![]()
瞪羚一般生活在沙漠和半沙漠、干旱的草原、树木繁茂的稀树草原、灌木丛生的草原、丘陵和浅林中。瞪羚是高度社会化的动物,所有的瞪羚都是群居的。一些群有多达700名成员,尽管一些瞪羚群很小并且按性别隔离。例如,雌性和年轻的幼羚生活在一起,还生活在10-30只雌性的群中。雄性单独生活或自己组群与其他雄性一起生活。雄性族群被称为单身汉族群。在迁徙过程中,雌雄混群,在交配季节,畜群的隔离更为突出,但只要有繁殖机会,它们就会被领地雄性分开。
瞪羚优化算法包含全局搜索,局部搜索和瞪羚逃生三个阶段:
1.1、种群随机初始化
Elite = [ x 1 , 1 ′ x 1 , 2 ′ ⋯ x 1 , d − 1 ′ x 1 , d ′ x 2 , 1 ′ x 2 , 2 ′ ⋯ x 2 , d − 1 ′ x 2 , d ′ ⋮ ⋮ x i , j ′ ⋮ ⋮ x n , 1 ′ x n , 2 ′ ⋯ x n , d − 1 ′ x n , d ′ ] \text { Elite }=\left[\begin{array}{lllll} x_{1,1}^{\prime} & x_{1,2}^{\prime} & \cdots & x_{1, d-1}^{\prime} & x_{1, d}^{\prime} \\ x_{2,1}^{\prime} & x_{2,2}^{\prime} & \cdots & x_{2, d-1}^{\prime} & x_{2, d}^{\prime} \\ \vdots & \vdots & x_{i, j}^{\prime} & \vdots & \vdots \\ x_{n, 1}^{\prime} & x_{n, 2}^{\prime} & \cdots & x_{n, d-1}^{\prime} & x_{n, d}^{\prime} \end{array}\right] Elite =⎣⎢⎢⎢⎡x1,1′x2,1′⋮xn,1′x1,2′x2,2′⋮xn,2′⋯⋯xi,j′⋯x1,d−1′x2,d−1′⋮xn,d−1′x1,d′x2,d′⋮xn,d′⎦⎥⎥⎥⎤
其中, x i , j = rand × ( U B j − L B j ) + L B j x_{i, j}=\operatorname{rand} \times\left(\mathrm{UB}_{j}-\mathrm{LB}_{j}\right)+\mathrm{LB}_{j} xi,j=rand×(UBj−LBj)+LBj
瞪羚优化算法中涉及布朗运动及莱维飞行:
1.1.1布朗运动
布朗运动是悬浮微粒被分子撞击后做无规则运动。布朗运动是将看起来连成一片的液体,在高倍显微镜下看其实是由许许多多分子组成的。液体分子不停地做无规则的运动,不断地随机撞击悬浮微粒。当悬浮的微粒足够小的时候,由于受到的来自各个方向的液体分子的撞击作用是不平衡的。在某一瞬间,微粒在另一个方向受到的撞击作用超强的时候,致使微粒又向其它方向运动,这样就引起了微粒的无规则的运动,即布朗运动。布朗运动满足正态(高斯)概率分布函数:
f B ( x ; μ , σ ) = 1 2 π σ 2 exp ( − ( x − μ ) 2 2 σ 2 ) = 1 2 π exp ( − x 2 2 ) f_{B}(x ; \mu, \sigma)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)=\frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{x^{2}}{2}\right) fB(x;μ,σ)=2πσ21exp(−2σ2(x−μ)2)=2π1exp(−2x2)
1.1.2莱维飞行
莱维飞行以法国数学家保罗·莱维命名,指的是步长的概率分布为重尾分布的随机行走,也就是说在随机行走的过程中有相对较高的概率出现大跨步。与步长分布没有重尾的随机行走相比,莱维飞行的运动轨迹就像时不时可以飞行一样,故名。当随机行走的空间维数高于一维时,莱维飞行通常还要求步长分布是各向同性的。
L ( x j ) ≈ ∣ x j ∣ 1 − α L\left(x_{j}\right) \approx\left|x_{j}\right|^{1-\alpha} L(xj)≈∣xj∣1−α
f L ( x ; α , γ ) = 1 π ∫ 0 ∞ exp ( − γ q α ) cos ( q x ) δ q f_{L}(x ; \alpha, \gamma)=\frac{1}{\pi} \int_{0}^{\infty} \exp \left(-\gamma q^{\alpha}\right) \cos (\mathrm{qx}) \delta q fL(x;α,γ)=π1∫0∞exp(−γqα)cos(qx)δq
Levy ( α ) = 0.05 × x ∣ y ∣ 1 α \operatorname{Levy}(\alpha)=0.05 \times \frac{x}{|y|^{\frac{1}{\alpha}}} Levy(α)=0.05×∣y∣α1x
其中, σ x = [ Γ ( 1 + α ) sin ( π α 2 ) Γ ( ( 1 + α ) 2 ) α 2 ( α − 1 ) 2 ] 1 / α , σ y = 1 , α = 1.5 , x = Normal ( 0 , σ x 2 ) , y = Normal ( 0 , σ y 2 ) \sigma_{x}=\left[\frac{\Gamma(1+\alpha) \sin \left(\frac{\pi \alpha}{2}\right)}{\Gamma\left(\frac{(1+\alpha)}{2}\right) \alpha 2^{\frac{(\alpha-1)}{2}}}\right]^{1 / \alpha},\sigma_{y}=1, \alpha=1.5,x=\operatorname{Normal}\left(0, \sigma_{x}^{2}\right) , y=\operatorname{Normal}\left(0, \sigma_{y}^{2}\right) σx=[Γ(2(1+α))α22(α−1)Γ(1+α)sin(2πα)]1/α,σy=1,α=1.5,x=Normal(0,σx2),y=Normal(0,σy2)
1.2、全局搜索
该阶段模拟瞪羚在没有捕食者或者捕食者跟踪情形下的自由放牧,瞪羚采取布朗运动,其位置更新如下:
![]()
gazelle i + 1 = gazelle i + S . R ∗ . R B ∗ ( Elite i − R B ∗ gazelle i ) \text { gazelle }_{i+1}=\text { gazelle }_{i}+S . R * . R_{B} *\left(\text { Elite }_{i}-R_{B} * \text { gazelle } _{i})\right. gazelle i+1= gazelle i+S.R∗.RB∗( Elite i−RB∗ gazelle i)
其中,S表示瞪羚的移动速度, R B R_{B} RB表示基于布朗运动的随机向量,R是在取值为0~1之间的随数。
1.3、局部搜索
该阶段模拟瞪羚发现捕食者后的逃跑行为,分为两个阶段,并且每个阶段都依据迭代次数的奇偶性而采取两种相反运动。第一阶段:瞪羚在发现捕食者前期采取莱维飞行;第二阶段:瞪羚在发现捕食者后期采取布朗运动。
![]()
1.3.1第一阶段
瞪羚在发现捕食者的前期采取莱维飞行:
gazelle i + 1 = gazelle i + S ⋅ μ ⋅ R ∗ ⋅ R L ∗ . ( Elite i − R L ∗ gazelle i ) \text { gazelle }_{i+1}=\text { gazelle }_{i}+S \cdot \mu \cdot R * \cdot R_{L} * \text {. }\left(\text { Elite }_{i}-R_{L} * \text { gazelle }_{i}\right) gazelle i+1= gazelle i+S⋅μ⋅R∗⋅RL∗. ( Elite i−RL∗ gazelle i)
其中, μ \mu μ为-1或1,表示两种运动方向; R L R_{L} RL表示基于 Lévy 分布的随机数向量。
1.3.2第二阶段
瞪羚在发现捕食者的后期采取布朗运动:
gazelle i + 1 = gazelle i + S ⋅ μ ⋅ C F ∗ . R B ∗ ( Elite i − R L ∗ ⋅ gazelle i ) \text { gazelle }_{i+1}=\text { gazelle }_{i}+S \cdot \mu \cdot CF * . R_{B} *\left(\text { Elite }_{i}-R_{L} * \cdot \text { gazelle }_{i}\right) gazelle i+1= gazelle i+S⋅μ⋅CF∗.RB∗( Elite i−RL∗⋅ gazelle i)
其中, C F = ( 1 − i t e r Maxiter ) ( 2 iter Maxiter ) C F=\left(1-\frac{i t e r}{\text { Maxiter }}\right)^{\left(2 \frac{\text { iter }}{\text { Maxiter }}\right)} CF=(1− Maxiter iter)(2 Maxiter iter )表示捕食者的累积效应。
1.4、瞪羚逃生
瞪羚面对捕食者时的存活率为0.66,这意味着捕食者有34%的机会狩猎成功,用PSRs表示捕食者的狩猎成功率,并以此对瞪羚逃生过程建立数学模型:
gazelle i + 1 = { gazelle i + C F [ L B + R ∗ . ( U B − L B ) ] ∗ . U if r ≤ P S R s gazelle i + [ P S R s ( 1 − r ) + r ] ( gazell r 1 − gazelle r 2 ) else \text { gazelle }_{i+1}=\left\{\begin{array}{ll} \text { gazelle }_{i}+C F[L B+R * .(U B-L B)] * . U & \text { if } r \leq P S R s \\ \text { gazelle }_{i}+[P S R s(1-r)+r]\left(\text { gazell }_{r_{1}}-\text { gazelle }_{r_{2}}\right) & \text { else } \end{array}\right. gazelle i+1={ gazelle i+CF[LB+R∗.(UB−LB)]∗.U gazelle i+[PSRs(1−r)+r]( gazell r1− gazelle r2) if r≤PSRs else
其中,r为0~1之间的随机数。
1.5、GOA算法描述
![]()
1.6、GOA算法流程
![]()
参考文献:Agushaka, J.O., Ezugwu, A.E. & Abualigah, L. Gazelle optimization algorithm: a novel nature-inspired metaheuristic optimizer. Neural Comput & Applic (2022). https://doi.org/10.1007/s00521-022-07854-6
二、旅行商问题
旅行商问题(Traveling salesman problem, TSP)是一个经典的组合优化问题,它可以描述为一个商品推销员去若干城市推销商品,要求遍历所有城市后回到出发地,目的是选择一个最短的路线。当城市数目较少时,可以使用穷举法求解。而随着城市数增多,求解空间比较复杂,无法使用穷举法求解,因此需要使用优化算法来解决TSP问题。
一般地,TSP问题可描述为:一个旅行商需要拜访n个城市,城市之间的距离是已知的,若旅行商对每个城市必须拜访且只拜访一次,求旅行商从某个城市出发并最终回到起点的一条最短路径。
记n个城市序号构成集合为N={1,2,…,n},旅行商拜访完n个城市所经过的回路记为:
P = { p 1 → p 2 → ⋯ → p n → p 1 } P=\left\{p_{1} \rightarrow p_{2} \rightarrow \cdots \rightarrow p_{n} \rightarrow p_{1}\right\} P={p1→p2→⋯→pn→p1}
其中, p i ∈ N , p i ≠ p j ( i ≠ j ) , i = 1 , 2 , ⋯ , n p_{i} \in N, p_{i} \neq p_{j}(i \neq j), i=1,2, \cdots, n pi∈N,pi=pj(i=j),i=1,2,⋯,n
若城市之间的距离矩阵为 D = ∣ d i j ∣ n × n D=\left|d_{i j}\right|_{n \times n} D=∣dij∣n×n,则TSP问题的数学模型可表示为:
min f ( P ) = ∑ i = 1 n − 1 d p i , p i + 1 + d p n , p 1 \min f(P)=\sum_{i=1}^{n-1} d_{p_{i}, p_{i+1}}+d_{p_{n}, p_{1}} minf(P)=i=1∑n−1dpi,pi+1+dpn,p1
其中, f ( P ) f(P) f(P)表示旅行商行走路线的总路径长度。
三、GOA求解TSP
本文选取国际通用的TSP实例库TSPLIB中的测试集bayg29为例,bayg29中城市分布如下图所示:

本文采用瞪羚优化算法求解bayg29:
close all
clear
clc
%数据集参考文献 REINELT G.TSPLIB-a traveling salesman problem[J].ORSA Journal on Computing,1991,3(4):267-384.
global data
% TSP数据集bayg29
Dim=size(data,1)-1;%维度
lb=-10;%下界
ub=10;%上界
fobj=@Fun;%计算训练集上的函数值(真实值与预测值的均方误差MSE)
SearchAgents_no=100; % 种群大小(可以修改)
Max_iteration=3000; % 最大迭代次数(可以修改)
[bestX,fMin,curve]=GOA(SearchAgents_no,Max_iteration,lb,ub,Dim,fobj); %瞪羚优化算法
figure
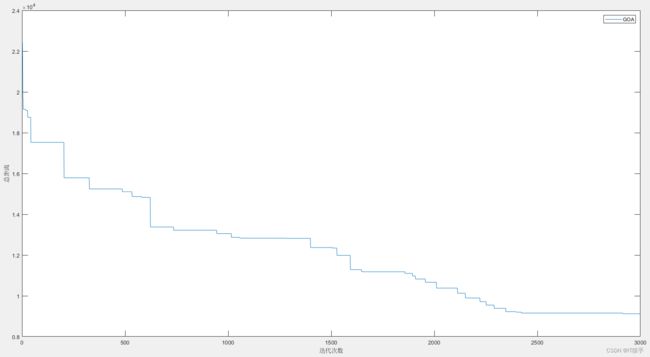
plot(curve)
xlabel('迭代次数')
ylabel('总距离')
legend('GOA')
链接:https://pan.baidu.com/s/11I6eMyMU3k-UHfUu1O_mIA
提取码:1234
部分结果如下:
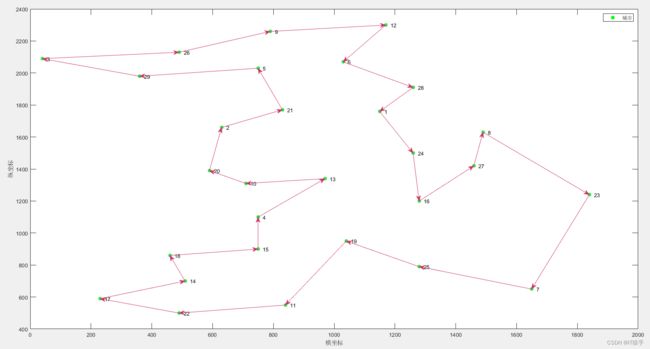
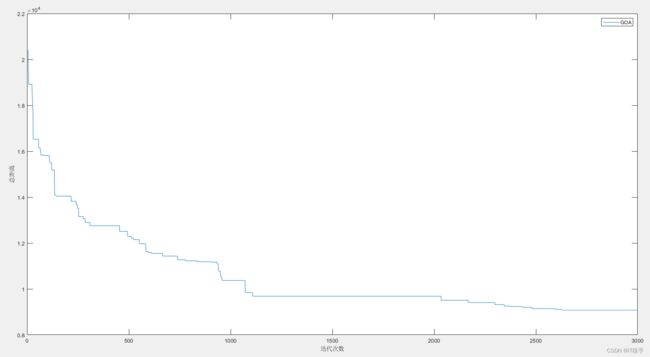
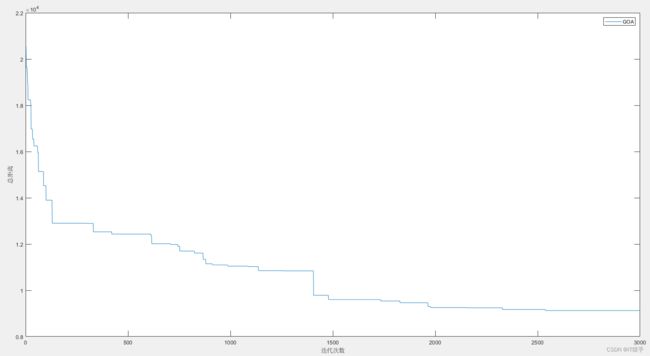
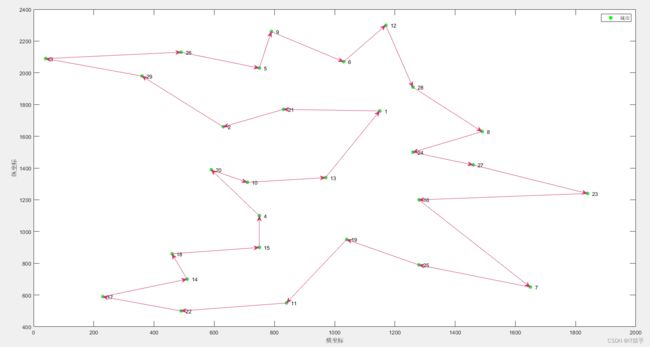
3.1第一次路径规划结果及算法收敛曲线
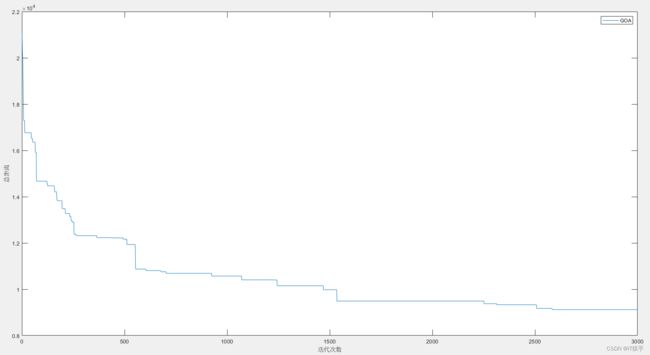
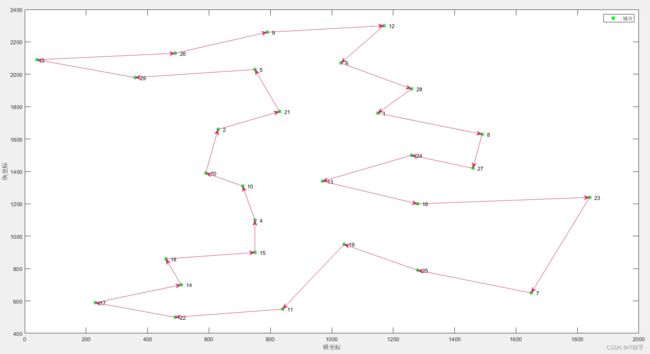
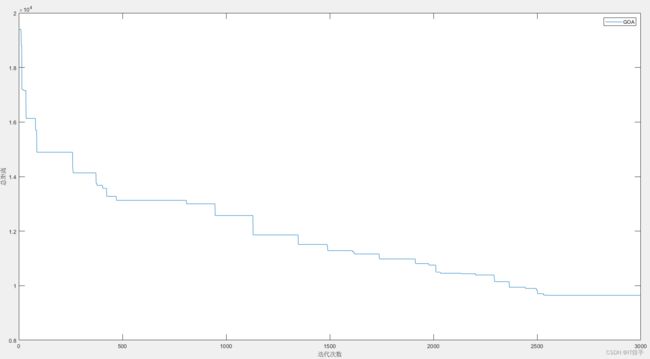
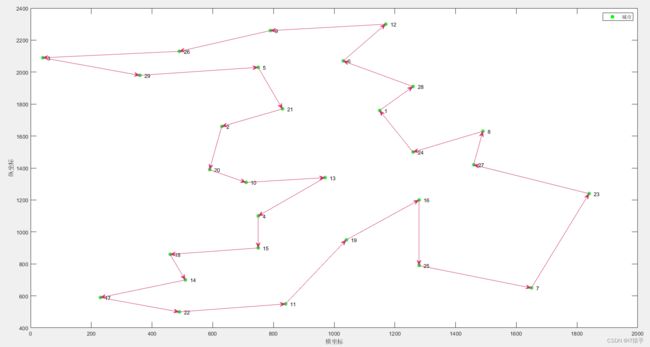
3.2第二次路径规划结果及算法收敛曲线
3.3第三次路径规划结果及算法收敛曲线
3.4第四次路径规划结果及算法收敛曲线
3.5第五次路径规划结果及算法收敛曲线
3.6第六次路径规划结果及算法收敛曲线
四、参考代码
文件夹内包含瞪羚优化算法GOA求解旅行商问题bayg29的完整Matlab代码,点击main.m即可运行,可以更改数据集。