这里有个物理信息神经网络开源项目:含模型、软件、论文
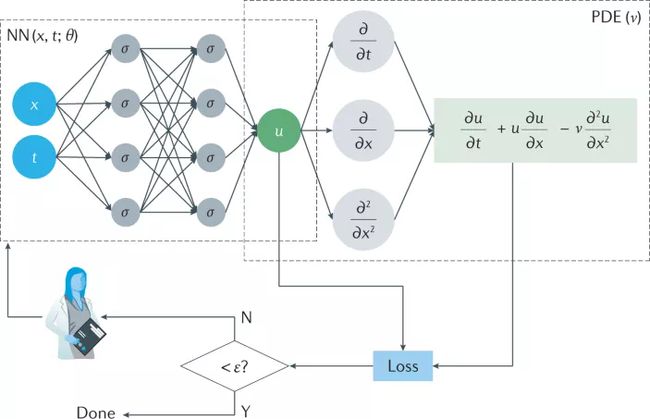
物理信息神经网络(Physics-Informed Neural Network,PINN)是由布朗大学应用数学的研究团队提出的一种用物理方程作为运算限制的神经网络,用于求解偏微分方程。
偏微分方程是物理中常用的用于分析状态随时间改变的物理系统的公式,该神经网络也因此成为 AI 物理领域中最常见到的框架之一。
PINN 架构图
近两年,PINN 在科学计算领域取得了巨大的成功。来自智能设计与鲁棒学习(IDRL)实验室创建了一个 github repo,列出了关于 PINN 的代表性工作。大家可以star、使用!(欢迎指正和建议。)
为方便起见,还提供了用于将 bibtex 转换为 markdown 的脚本。
项目地址:https://github.com/idrl-lab/PINNpapers
以下为项目内容列表:
软件
-
DeepXDE: A Deep Learning Library for Solving Differential Equations, Lu Lu, Xuhui Meng, Zhiping Mao, George Em Karniadakis, SIAM Review, 2021.
-
NVIDIA SimNet™: An AI-Accelerated Multi-Physics Simulation Framework, Oliver Hennigh, Susheela Narasimhan, Mohammad Amin Nabian, Akshay Subramaniam, Kaustubh Tangsali, Zhiwei Fang, Max Rietmann, Wonmin Byeon, Sanjay Choudhry, ICCS, 2021.
-
SciANN: A Keras wrapper for scientific computations and physics-informed deep learning using artificial neural networks, Ehsan Haghighat, Ruben Juanes, arXiv preprint arXiv:2005.08803, 2020.
-
Elvet -- a neural network-based differential equation and variational problem solver, Jack Y. Araz, Juan Carlos Criado, Michael Spannowsky, arXiv:2103.14575 [hep-lat, physics:hep-ph, physics:hep-th, stat], 2021.
-
TensorDiffEq: Scalable Multi-GPU Forward and Inverse Solvers for Physics Informed Neural Networks, Levi D. McClenny, Mulugeta A. Haile, Ulisses M. Braga-Neto, arXiv:2103.16034 [physics], 2021.
-
PyDEns: a Python Framework for Solving Differential Equations with Neural Networks, Alex Koryagin, er, Roman Khudorozkov, Sergey Tsimfer, arXiv:1909.11544 [cs, stat], 2019.
-
NeuroDiffEq: A Python package for solving differential equations with neural networks, Feiyu Chen, David Sondak, Pavlos Protopapas, Marios Mattheakis, Shuheng Liu, Devansh Agarwal, Marco Di Giovanni, Journal of Open Source Software, 2020.
-
Universal Differential Equations for Scientific Machine Learning, Christopher Rackauckas, Yingbo Ma, Julius Martensen, Collin Warner, Kirill Zubov, Rohit Supekar, Dominic Skinner, Ali Ramadhan, Alan Edelman, arXiv:2001.04385 [cs, math, q-bio, stat], 2020.
-
NeuralPDE: Automating Physics-Informed Neural Networks (PINNs) with Error Approximations, Kirill Zubov, Zoe McCarthy, Yingbo Ma, Francesco Calisto, Valerio Pagliarino, Simone Azeglio, Luca Bottero, Emmanuel Luján, Valentin Sulzer, Ashutosh Bharambe, N Vinchhi, , Kaushik Balakrishnan, Devesh Upadhyay, Chris Rackauckas, arXiv:2107.09443 [cs], 2021.
-
IDRLnet: A Physics-Informed Neural Network Library, Wei Peng, Jun Zhang, Weien Zhou, Xiaoyu Zhao, Wen Yao, Xiaoqian Chen, arXiv:2107.04320 [cs, math], 2021.
PINN 模型
-
Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, M. Raissi, P. Perdikaris, G. E. Karniadakis, Journal of Computational Physics, 2019.
-
The deep Ritz method: a deep learning-based numerical algorithm for solving variational problems, E Weinan, Bing Yu, Communications in Mathematics and Statistics, 2018.
-
DGM: A deep learning algorithm for solving partial differential equations, Justin Sirignano, Konstantinos Spiliopoulos, Journal of Computational Physics, 2018.
-
SPINN: Sparse, Physics-based, and partially Interpretable Neural Networks for PDEs, Amuthan A. Ramabathiran, Ramach, Prabhu ran, Journal of Computational Physics, 2021.
并行 PINN
-
Parallel Physics-Informed Neural Networks via Domain Decomposition, Khemraj Shukla, Ameya D. Jagtap, George Em Karniadakis, arXiv:2104.10013 [cs], 2021.
-
Finite Basis Physics-Informed Neural Networks (FBPINNs): a scalable domain decomposition approach for solving differential equations, Ben Moseley, Andrew Markham, Tarje Nissen-Meyer, arXiv:2107.07871 [physics], 2021.
-
PPINN: Parareal physics-informed neural network for time-dependent PDEs, Xuhui Meng, Zhen Li, Dongkun Zhang, George Em Karniadakis, Computer Methods in Applied Mechanics and Engineering, 2020.
PINN 加速
-
Self-adaptive loss balanced Physics-informed neural networks for the incompressible Navier-Stokes equations, Zixue Xiang, Wei Peng, Xiaohu Zheng, Xiaoyu Zhao, Wen Yao, arXiv:2104.06217 [physics], 2021.
-
A Dual-Dimer method for training physics-constrained neural networks with minimax architecture, Dehao Liu, Yan Wang, Neural Networks, 2021.
-
Adversarial Multi-task Learning Enhanced Physics-informed Neural Networks for Solving Partial Differential Equations, Pongpisit Thanasutives, Masayuki Numao, Ken-ichi Fukui, arXiv:2104.14320 [cs, math], 2021.
-
DPM: A Novel Training Method for Physics-Informed Neural Networks in Extrapolation, Jungeun Kim, Kookjin Lee, Dongeun Lee, Sheo Yon Jin, Noseong Park, AAAI, 2021.
模型迁移和元学习
-
A physics-aware learning architecture with input transfer networks for predictive modeling, Amir Behjat, Chen Zeng, Rahul Rai, Ion Matei, David Doermann, Souma Chowdhury, Applied Soft Computing, 2020.
-
Transfer learning based multi-fidelity physics informed deep neural network, Souvik Chakraborty, Journal of Computational Physics, 2021.
-
Transfer learning enhanced physics informed neural network for phase-field modeling of fracture, Somdatta Goswami, Cosmin Anitescu, Souvik Chakraborty, Timon Rabczuk, Theoretical and Applied Fracture Mechanics, 2020.
-
Meta-learning PINN loss functions, Apostolos F. Psaros, Kenji Kawaguchi, George Em Karniadakis, arXiv:2107.05544 [cs], 2021.
概率 PINN 和不确定性量化
-
A physics-aware, probabilistic machine learning framework for coarse-graining high-dimensional systems in the Small Data regime, Constantin Grigo, Phaedon-Stelios Koutsourelakis, Journal of Computational Physics, 2019.
-
Adversarial uncertainty quantification in physics-informed neural networks, Yibo Yang, Paris Perdikaris, Journal of Computational Physics, 2019.
-
B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data, Liu Yang, Xuhui Meng, George Em Karniadakis, Journal of Computational Physics, 2021.
-
PID-GAN: A GAN Framework based on a Physics-informed Discriminator for Uncertainty Quantification with Physics, Arka Daw, M. Maruf, Anuj Karpatne, arXiv:2106.02993 [cs, stat], 2021.
-
Quantifying Uncertainty in Physics-Informed Variational Autoencoders for Anomaly Detection, Marcus J. Neuer, ESTEP, 2020.
应用
-
Physics-informed neural networks for high-speed flows, Zhiping Mao, Ameya D. Jagtap, George Em Karniadakis, Computer Methods in Applied Mechanics and Engineering, 2020.
-
Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data, Luning Sun, Han Gao, Shaowu Pan, Jian-Xun Wang, Computer Methods in Applied Mechanics and Engineering, 2020.
-
Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations, Maziar Raissi, Alireza Yazdani, George Em Karniadakis, Science, 2020.
-
NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations, Xiaowei Jin, Shengze Cai, Hui Li, George Em Karniadakis, Journal of Computational Physics, 2021.
-
A High-Efficient Hybrid Physics-Informed Neural Networks Based on Convolutional Neural Network, Zhiwei Fang, IEEE Transactions on Neural Networks and Learning Systems, 2021.
-
A Study on a Feedforward Neural Network to Solve Partial Differential Equations in Hyperbolic-Transport Problems, Eduardo Abreu, Joao B. Florindo, ICCS, 2021.
PINN 分析
-
Estimates on the generalization error of physics-informed neural networks for approximating a class of inverse problems for PDEs, Siddhartha Mishra, Roberto Molinaro, IMA Journal of Numerical Analysis, 2021.
-
Error analysis for physics informed neural networks (PINNs) approximating Kolmogorov PDEs, Tim De Ryck, Siddhartha Mishra, arXiv:2106.14473 [cs, math], 2021.
-
Error Analysis of Deep Ritz Methods for Elliptic Equations, Yuling Jiao, Yanming Lai, Yisu Luo, Yang Wang, Yunfei Yang, arXiv:2107.14478 [cs, math], 2021.
项目地址:https://github.com/idrl-lab/PINNpapers