FCOS要点解析

写在前面
FCOS是Fully Convlutional One-Stage的缩写。最初版论文在2019年提出，2020年做了修改。正如它的名字，这是一个在目标检测领域重要的全卷积+one-stage模型，更重要的是它还摒弃了anchors，原因是作者认为anchors会带给模型样本不均衡和计算开销增加等问题。也就是说FCOS既没有proposals或者ROI Pooling操作，也没有anchors来预先框住目标。本博客也是本人的学习笔记。
这里是参考文章和视频教学

---

一、Anchor-free模型

1. Anchor-based模型弊端

在anchor-based模型中，例如YOLOV2、R-CNN家族系列等，无论是在训练还是测试阶段，都先是在输入图片上生成一系列密集的anchors，然后再根据这些anchors去对其内部的目标进行分类，对其边界框参数进行回归，预测阶段在经过NMS处理得到最终的输出。FCOS作者认为庞大的anchors数量给模型带来了弊端，主要是以下4点：

1. Anchors的超参数设置玄学，例如size和ratio等，稍不注意便会带来模型效果的变化。

2. Anchors的size和ratio由于是超参数，在模型中是固定不变的，导致模型难以处理同一物体放置角度导致形状变化较大的情况。并且在迁移到其他数据集时容易出现需要重新设置这些超参数。

3. 由于模型追求高recall（查全率），anchors往往生成的过量，这会导致出现正负样本严重不均，导致类别不平衡问题。

4. Anchors的分配过程会产生额外计算开销（计算其与GT bbox的IoU）。

2. Anchor-free

于是，FCOS模型摒弃了anchors的概念，转而直接去回归预测边界框的4D vector参数。此参数会在回归分支里去计算。

如上图所示，边界框的4D vector分别为{l, r, t, b}，分别代表图上某点与它所预测的边界框的4个边框的距离（在原图尺度上）。训练过程中则代表此点与被分配到的GT bbox的边框的距离。点与GT bbox的分配详见正负样本匹配部分。

---

二、正负样本匹配以及assign

1. 正负样本匹配

基于anchor的模型训练样本是原图尺度上生成的一系列anchors，根据anchors与GT bbox的IoU来决定正负样本的分配。而FCOS是anchor-free的模型，直接针对特征图上的每个location进行训练。这就涉及到这些locations的正负样本匹配问题。

首先我们知道，feature map上某一点（x, y）可以根据公式$(\lfloor \frac{s}{2}\rfloor +xs,\lfloor \frac{s}{2}\rfloor +ys)$计算出其在原图上的坐标。其中s代表feature map与原图的步距。

其次，我们也知道GT bboxes的边界框信息$B_i=(x_0^{(i)},y_0^{(i)},x_1^{(i)},y_1^{(i)})$，分别代表GT框左上角点与右下角点在原图上的坐标。在最新的论文里，作者对每个GT bbox都计算一个sub-box：根据GT bbox的中心坐标$(c_x,c_y)$，可以计算出其sub-box左上角右下角坐标$(c_x-rs,c_y-rs,c_x+rs,c_x+rs)$，其中$r$是超参数，与数据集相关，作者在论文里做了此超参数取值的一系列实验，在COCO数据集上设置为1.5较好（此部分可在论文中详细了解）。

根据上文，匹配方式即为：计算feature map上点在原图上的对应坐标，如果该坐标落入某个sub-box内，则该点被分配为正样本，并且负责该目标的检测；若没有落入任何一个sub-box，则分配为负样本。论文称之为 center sampling机制。（2019年老版本论文里无sub-box概念，只要落入GT bbox内即分配为正样本）

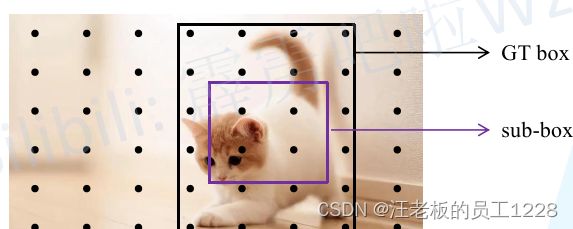
这样其实会产生一个疑问：要是一个点同时落入多个sub-box内该如何分配呢？ 这就是论文中所谓的ambiguity问题，即样本匹配模糊问题。此问题的介绍和解决将在下面介绍。

2. Assign中的ambiguity问题

Ambiguity问题其实就是：正样本匹配过程中存在落入多个GT bbox范围内时，到底该分配至哪一个目标？ (如下图所示点就同时落入了两个GT bbox内）此问题处理不好的话，会影响模型最终的查全率（racall）。

其实由于FCOS结构的设置，ambiguity问题出现概率已被降低到很小。这主要归功于 ：“1）不同尺寸目标在FPN不同levels上分级检测” ；“2）center sampling机制” 。

• FPN不同levels上目标的分级检测
  一句话总结，就是不同尺寸大小的目标在不同level上被当成正样本传给head计算。这与之前基于anchor的模型中的想法是一致的。论文中给出了具体分级的细节，这里需要先引入边界框4D vector的GT值$(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$，此值的计算详见回归分支损失函数部分，这里我们先默认已经计算得到。

  在训练过程中，先进行正负样本分配，再计算第$i$个level上所有正样本点对应的4D vector GT值$(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$。**如果某正样本点的GT值中的最大值，也就是$max(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$，不在第$i$个level设定的数值范围$(m_{i-1},m_i)$之间，则该正样本在第$i$个level上被设定为负样本。**换句话说就是：正样本点想在第$i$个level上保留住它的正样本身份，就必须满足其4D vector GT值$(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$ 中4个都在第$i$个level设定的数值范围$(m_{i-1},m_i)$之间。$i$的取值范围为$(3,4,5,6,7)$，对应P3~P7；$m_i$的取值为$(0,64,128,256,512,\infty )$，0对应$m_2$，$\infty$对应$m_7$。

  这样，不同尺寸的目标大概率不会在同一level都被当成正样本，减小了目标重叠的概率，也就降低了ambigiuty问题出现的概率。

• center sampling机制
  center sampling机制已在上文介绍。我们可以理解为center sampling机制缩小了每个目标管辖的区域，其实也就是减小了判定区域的重叠概率。

论文中作者研究了使用上述两种方法与否对ambiguity出现概率的影响。可以看到，使用 分级检测+center sampling机制 后，ambiguity问题出现概率已经被降低至3%以下（下表中最后一行）。

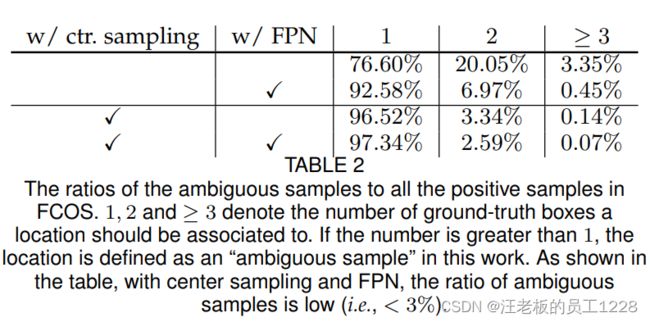
如果经过分级检测+center sampling机制，还有ambiguity问题出现，则简单地把该点分配给落入的面积最小的那个GT bbox（注意不是sub-box的面积）。

---

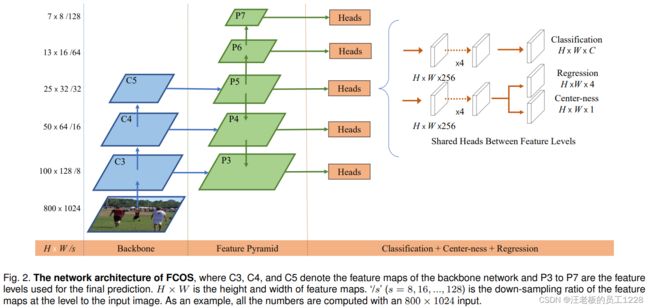
三、FCOS网络结构

1. Backbone

1.1 ResNet + FPN

Backbone借鉴RetinaNet中的形式，依旧是采用ResNet + FPN结构获得不同level的feature map：P3~P7。不过这里的P6生成方式与RetinaNet不同，RetinaNet中P6是在C5的基础上生成的，FCOS中则是在P5基础上进行下采样。下图有此部分的详细结构（图源博主）。

2. Head

Head部分接受backbone的输入，完成下游的分类与回归任务。值得注意的是，head在不同level的特征图输出上是共享的，即P3~P7这5个level的输出共用一个head。

Head有两个大分支：cls分类分支与reg边界框回归分支。值得注意的是，在reg分支最后一层还并行了一个center-ness分支来计算预测边界框的center-ness值。Head部分的详细结构如下图所示（图源博主），下面将分别介绍这三个分支。

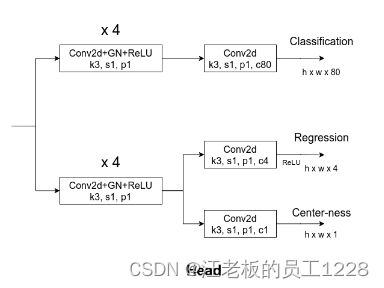
2.1 分类分支与回归分支

分类分支与回归分支大体上结构相似。在接受不同level的输入后，两分支都先经过四个卷积层模块的计算，每个卷积层模块中包括：1）3x3大小卷积 + 步距=1 + padding=1，channel不变；2）GN组归一化；3）ReLU激活函数。 得到的结果再经过一个“3x3大小卷积 + 步距=1 + padding=1”的卷积层之后：

• 对于分类分支，channel设置为类别数（论文中为80对应COCO数据集），输出代表每一点负责目标的softmax类别概率值cls score；
• 对于回归分支，不仅channel设置为4，还在最后输出前做了ReLU激活（因为4D vector的值总是大于0的），对应每一点负责目标边界框的4D vector（4D vector在前文已介绍）。

2.2 Center-ness计算分支

图中还有一个与回归分支最终卷积层并行的小分支，用于计算边界框的center-ness值。它与回归分支最终卷积层共享其前四个卷积层的输出，且它与回归分支最终卷积层结构上的差别仅体现在channel不同上：center-ness分支的channel为1。

下面介绍一下论文提出的center-ness值。

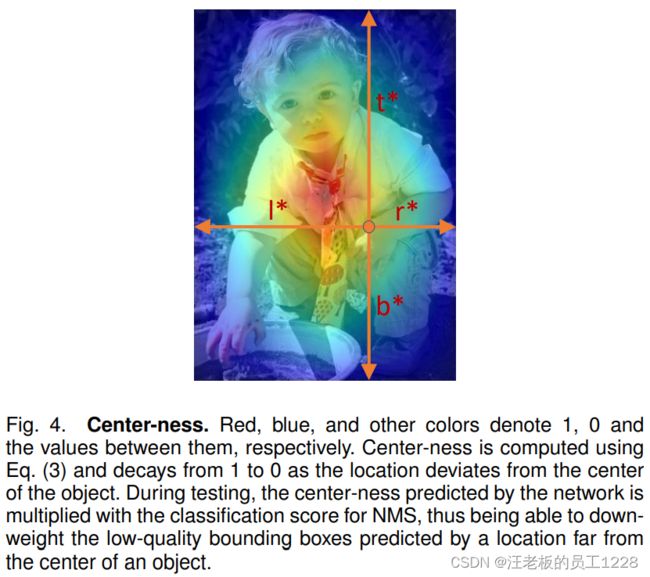
作者在实验过程中发现，模型在远离目标中心的位置上输出许多低质量的检测结果，为了提升模型效果，这些结果是需要被抑制的。于是作者提出了center-ness值，用来衡量特征图上点对应回原图之后，离其所分配的目标中心的一个归一化距离。对于某点，在计算其边界框4D vector的GT值$(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$后，根据以下公式计算GT center-ness值：

$$centernes{s}^{\ast }=\sqrt{\frac{min(l^{\ast },r^{\ast })}{max(l^{\ast },r^{\ast })}\times \frac{min(t^{\ast },b^{\ast })}{max(t^{\ast },b^{\ast })}}$$

由上述公式可以知道：当目标中心与映射回原图的点重合时，center-ness值为0；当离目标中心越远，center-ness值越接近1。论文中提到开根号是为了减缓center-ness的衰减。

在推理（测试）阶段，网络预测出的center-ness值会与分类分支预测出的cls score相乘后开根，也就是综合考虑类别得分和离目标中心距离后，再依据此值进行NMS过滤掉那些低质的检测结果。论文验证了center-ness分支的引入可以减小远离目标中心的位置上检测结果得分的权重，显著提高了模型效果，如下表第一行和最后一行对比所示。

这里也会有一个疑问：为什么要单独引出一个center-ness的计算分支来预测center-ness值，而不是使用每次回归分支的预测值带入$centernes{s}^{\ast }$公式计算center-ness值呢？ 作者为此也做了相关实验，对应上表中第二行结果，发现模型效果还比不上不使用center-ness的情况。说明解耦center-ness的计算和回归分支的预测，使用单独的center-ness分支是很有必要的。

---

四、损失函数及其计算

1. Head分支的GT值

1.1 分类分支GT

分类分支GT维度与head中输出channel维度一致，COCO数据集上为80维。若该点为负样本，则其分类GT值全为0；若为正样本，则其GT值为其负责预测的目标类别（one-hot向量）。

1.2 回归分支GT

回归分支GT仅针对与正样本存在。对于给定的某个feature map上某点，其在原图上对应坐标为$(x,y)$，该level的feature map与原图步距为$s$，该点负责（分配至）的目标边界框信息为$B_i=(x_0^{(i)},y_0^{(i)},x_1^{(i)},y_1^{(i)})$（GT bbox左上角以及右下角点），则该点回归分支的4D vector GT计算方式为：

$$\begin{gathered} l^{\ast }=(x-x_0^{(i)})/s,t^{\ast }=(y-y_0^{(i)})/s, \\ {r}^{\ast }=(x_1^{(i)}-x)/s,b^{\ast }=(y_1^{(i)}-y)/s, \end{gathered}$$

1.3 Center-ness GT

在前文 2.2 Center-ness计算分支 已经介绍，这里就不赘述了。

2. 损失函数

$$\begin{gathered} L(\{{\mathbf{p}}_{x,y}\},\{{\mathbf{t}}_{x,y}\},\{{\mathbf{s}}_{x,y}\})=\frac{1}{N_{pos}}\sum _{x,y}{L}_{cls}({\mathbf{p}}_{x,y},c_{x,y}^{\ast }) \\ +\frac{\lambda }{N_{pos}}\sum _{x,y}{1}_{\{c_{x,y}^{\ast }>0\}}{L}_{reg}({\mathbf{t}}_{x,y},{\mathbf{t}}_{x,y}^{\ast }) \\ +\frac{1}{N_{pos}}\sum _{x,y}{1}_{\{c_{x,y}^{\ast }>0\}}{L}_{ctrness}({\mathbf{s}}_{x,y},{\mathbf{s}}_{x,y}^{\ast }) \end{gathered}$$
损失函数由三部分组成：分类损失、边界回归损失以及center-ness损失。$\mathbf{p},\mathbf{t},\mathbf{s}$分别代表分类分支、回归分支以及center-ness分支的输出，带 * 号的为GT值。

• 分类损失
  分类损失对应等式右侧第一行，采用带focal loss的BCE损失（即BCE with focal loss）。计算时正负样本都要计算，最后除以正样本的个数。

• 边界框回归损失
  边界框回归损失对应等式右侧第二行，采用的是GIoU loss（老版本是IoU loss，GIoU loss已被证明在FCOS上效果更好）。计算时只计算正样本，也要除以正样本的个数，最后乘上一个平衡因子$\lambda$，论文中设置为1。

• center-ness损失
  center-ness损失对应等式右侧最后一行，采用BCE loss。计算时也是只计算正样本，最后除以正样本个数。