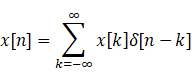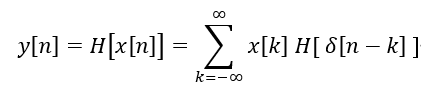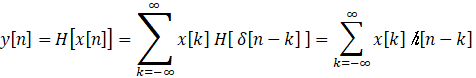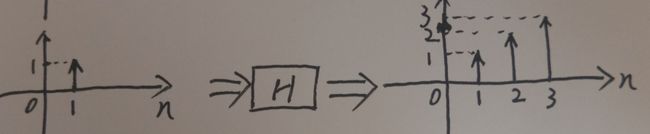详解卷积公式的物理意义
作者:Uncle Jack
日期:2020/03/15
分解思维
1. 人类科学有一个特点是喜欢使用分解的思维去理解分析很多复杂的事物,比如傅里叶级数把很多奇形怪状的函数分解成无穷多个三角函数,又比如力学分析中把单个力分解成直角坐标系中的的xy分量等等。如果要研究以时间为自变量的函数x[t]经过系统H后会输出什么这样的问题,也可以用分解的方法去看待
2. 从能量的角度看,任何信号都是由一份一份的基本能量所构成的,它们在时间轴上紧密排列,最后形成一条曲线,我们把它叫做x(t),纵轴为x(t),横轴为t,离散化之后叫x[n],因此信号一定是时间的函数。和我们平时经验积累起来的函数不同,平时做数学题的函数多为静态函数,也就是一个输入值对应一个输出值,这种函数当前的输出和历史的输入好像没什么关系。
3. 利用分解思维,我们也可以定义出最基本的能量单元,或者取名叫单位1能量,这样一来所有的信号都可以由这个单位1能量组成,这个单位1能量就是冲击函数δ(t),离散世界中叫做δ[n],这个函数将用来表示单位1的能量,甚至它生成的时间位置都有做归一化处理,即在时刻0(注意这里说的是时刻)上出现单位1的能量,其余任意时刻能量都为0,为了表述方便,这里用离散函数分析通用意义。
用冲击函数表示任意函数x[n]为:
因为只有当n=k时,δ[n-k]才为1,其余值都是0,所以等式是成立的。
这个公式的分析:
时刻上看:在任意时刻k,信号的能量值x[k]等于x[k]乘以1,看起来像是废话,但这里面透露的深层次信息为:信号x[k]已经被分解,改用单位1能量的倍数来表示
总时间上看:用单位1能量描绘了信号x[n]在时间轴上各个时刻的能量值大小
现在假设x[n]经过一个线性移不变系统H,输出为y[n],因为线性,所以下面等式成立:
又因为移不变性,所以下面等式成立:
其中h[n]是系统H的冲击响应函数,h[n-k]是第n-k时刻对应的冲击响应值
第一个关键的东西来了,冲击响应是什么?直观理解就是冲击信号通过系统之后的输出,这个输出函数同输入函数一样,也是带着一个时间自变量的信号。
所以冲击响应表示:时刻为0,值为单位1的能量在经过系统H后所输出能量的时间分布情况
理解了这个,我们可以把一个复杂信号x[n]经过系统H的输出描绘出来,通过下面的卷积分析可以帮助理解:
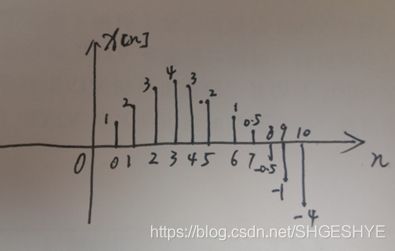
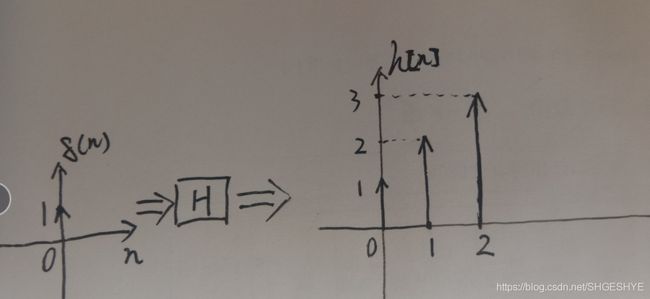
提问:假设线性移不变系统H的冲击响应为序列h[n]=[1, 2, 3],求序列x[n]=[1, 1, 1]经过H之后的输出y[n]
分析:冲击响应序列h[n]指明了单位能量信号在时刻0经过H后会分别在时刻0,时刻1,时刻2上产生大小分别为1,2,3的能量(假设是有源系统,不考虑能量守恒),也就是单位1的能量经过系统不仅仅会在当前时刻输出一个能量,还会分别在1个单位时间和2个单位时间之后的未来各自产生一个能量余威。
现在要求的是时刻0,时刻1和时刻2挨个挨个输入单位1的能量,总的输出是什么。
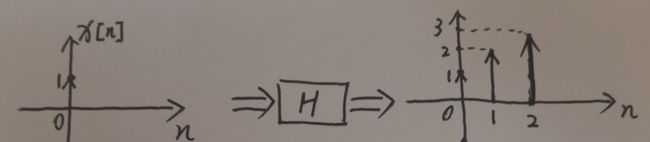
对于时刻0输入的产出,单位1能量在时刻0经过H,即等同于冲击响应
对于时刻1的产出,即单位1能量右移1单位时间经过H的输出,因为移不变性,所以输出应该是冲击响应整体右移1时间单位
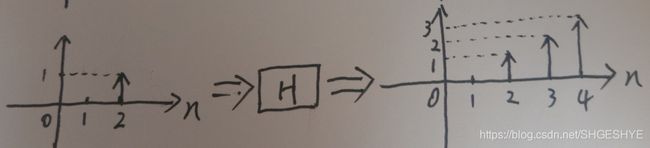
对于时刻2的产出,即单位1能量右移2单位时间经过H的输出,因为移不变性,所以输出应该是冲击响应整体右移2时间单位
对于其它时刻的产出,因为其余时刻输入都为0,所以产出也是0
我们注意到上面三个不同时刻输入的序列可能会在同一时刻都输出能量,比如:时刻0输入的响应会在时刻2上产生输出(值为3),时刻1输入的响应也会在时刻2上产生输出(值为2),时刻2的输入同样会在时刻2上产生输出(值为1),其余任意时刻也会在时刻2上产生输出(值为0), 那么时刻2的输出应是多少呢?因为他们产生的都是正值(相位相同或者方向一致),那么就应该是所有加在这上面的能量的总和,应该叠加起来就是这个时刻的最终能量大小
输出y[n]信号描述的是所有时刻能量值的大小,我们可以通过y[n]查找到任意时刻的能量值。所以最终的输出就应该是把时刻0,时刻1和时刻2(其余时刻都为0,就不描述了)的输入所对应的输出能量进行叠加即可,叠加的方法应该按照各个时刻进行,如下图:
序列表示即:y[n]=[0,0,…0,1,3,6,5,3,0,0,…,0],去掉那些无值的点只表示t=0,t=1,.., t=4,即为[1, 3, 6, 5, 3],这个结果和书上所用的反褶方法计算的结果是一样的,但是这个方法更利于对卷积的理解
这里使用的x[n]能量值都是单位1,如果是别的值也是一样的方法,只需要对冲击响应不同时刻下的值都乘以当前时刻x[n]的值即可。因为单位1能量输出为h[n],那么单位1的x[k]倍大小的能量对应的输出就应该为x[k]h[n]
总结:
- 系统会改变输入信号原有的时间-能量分布情况,从而实现对其进行重分配
- 系统当前时刻输出的能量值一定是当前时刻以及历史上各个时刻对应的输入信号能量在经过系统后蔓延到这一刻的值的叠加