Python学习4-谱聚类

一，谱聚类原理

谱聚类算法原理可以参考如下链接。

这个视频推导出了拉普拉斯矩阵，但没有更新后续优化问题。

机器学习-白板推导系列(二十二)-谱聚类（Spectral Clustering）_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1kt411X7Zh?from=search&seid=10058510101134916284&spm_id_from=333.337.0.0可以搭配视频笔记食用：

谱聚类 · 语雀 (yuque.com)https://www.yuque.com/books/share/f4031f65-70c1-4909-ba01-c47c31398466/wkk1g3详细及全面讲解参考：

(6条消息) 带你玩转谱聚类及拉普拉斯矩阵_SL_World的博客-CSDN博客https://blog.csdn.net/SL_World/article/details/104423536

(6条消息) 谱聚类（spectral clustering)及其实现详解_yycc-CSDN博客_谱聚类实现https://blog.csdn.net/yc_1993/article/details/52997074

谱聚类是从图论中演化出来的算法，后来在聚类中得到了广泛的应用。

1，构图

谱聚类过程主要有两步，第一步是构图，将采样点数据构造成一张网图，表示为G(V,E)，V表示图中的点，E表示点与点之间的边，如下图：

  图1 谱聚类构图(来源wiki)

在构图中，一般有三种构图方式：
       1. ε-neighborhood
       2. k-nearest neighborhood
       3. fully connected

2，切图

第二步是切图，即将第一步构造出来的按照一定的切边准则，切分成不同的图，而不同的子图，即我们对应的聚类结果，举例如下：

          谱聚类切图存在两种主流的方式：RatioCut和Ncut，目的是找到一条权重最小，又能平衡切出子图大小的边。

二，实现

（一），自写Python实现步骤

 参考：谱聚类（Spectral Clustering）原理及Python实现_songbinxu的博客-CSDN博客_谱聚类python代码https://blog.csdn.net/songbinxu/article/details/80838865

 0.生成数据（utils/dataloader.py）

from sklearn import datasets
#sklearn 学习参考网址https://zhuanlan.zhihu.com/p/393113910

def genTwoCircles(n_samples=1000):
    X,y = datasets.make_circles(n_samples, factor=0.5, noise=0.05)
    return X, y
'''
 datasets.make_circles在2d中创建一个包含较小圆的大圆的样本集
 factor内圈和外圈之间的比例因子
 noise高斯噪声的标准偏差加到数据上
 返回：
 X生成的样本
 y每个样本的类成员的整数标签（0或1）
'''

1.距离矩阵(utils/similarity.py)

import numpy as np
#定义欧式距离
def euclidDistance(x1, x2, sqrt_flag=False):
    res = np.sum((x1-x2)**2)
    if sqrt_flag:
        res = np.sqrt(res)
    return res

def calEuclidDistanceMatrix(X):
    X = np.array(X)
    S = np.zeros((len(X), len(X)))
    for i in range(len(X)):
        for j in range(i+1, len(X)):
            S[i][j] = 1.0 * euclidDistance(X[i], X[j])
            S[j][i] = S[i][j]
    return S
    
'''
 np.array:创建数组,array 里的元素都是同一类型
 返回：
 S距离矩阵
'''

 2.临街矩阵(utils/knn.py)

'''
KNN算法：
  如果一个样本在特征空间中的K个最相似（即特征空间中最邻近）的样本中的大多数
  属于某一个类别，则该样本也属于这个类别。
  该方法在定类决策上只依据最邻近的一个或者几个样本的类别
  来决定待分样本所属的类别
'''
import numpy as np

def myKNN(S, k, sigma=1.0):
    N = len(S)
    #返回矩阵的行数
    A = np.zeros((N,N))
#下为找xi的K邻近
    for i in range(N):
        dist_with_index = zip(S[i], range(N))
        #矩阵的第i行各个元素，与长度为数字N的tuple（元组）集合，组成列表
        #[(ai1,0),(ai2,1),,,]
        dist_with_index = sorted(dist_with_index, key=lambda x:x[0])
        #按列表的第一个元素升序排列
        neighbours_id = [dist_with_index[m][1] for m in range(k+1)] 
        # xi's k-nearest neighbours
        #返回K邻近的列坐标
        for j in neighbours_id: # xj is xi's neighbour
            A[i][j] = np.exp(-S[i][j]/2/sigma/sigma)
            #高斯核函数:随着两个向量的距离增大，高斯核函数单调递减
            #np.exp=e^x
            A[j][i] = A[i][j] # mutually

    return A
'''
 A是各个样本的K邻近矩阵，维度:n*n,K邻近有值，其余为0
'''

 3. 标准化的拉普拉斯矩阵(utils/laplacian.py)

import numpy as np

def calLaplacianMatrix(adjacentMatrix):

    # compute the Degree Matrix: D=sum(A)
    degreeMatrix = np.sum(adjacentMatrix, axis=1)

    # print degreeMatrix

    # compute the Laplacian Matrix: L=D-A
    laplacianMatrix = np.diag(degreeMatrix) - adjacentMatrix
    #np.diag:以一维数组的形式返回方阵的对角线
    # print laplacianMatrix

    # normailze
    # D^(-1/2) L D^(-1/2)
    sqrtDegreeMatrix = np.diag(1.0 / (degreeMatrix ** (0.5)))
    #**:返回x的y次幂
    return np.dot(np.dot(sqrtDegreeMatrix, laplacianMatrix), sqrtDegreeMatrix) 
    #np.dot:矩阵乘法
    #假设A,B为矩阵，A.dot(B)等价于 np.dot(A,B)

4. 特征值分解、5. Kmeans (utils/main.py)

import sys

'''
 首先引入sys模块，sys模块提供了许多函数和变量来处理 Python运行时环境的不同部分
 sys 模块主要负责与 Python 解释器进行交互，该模块提供了一系列用于控制 Python 运行环境的函数和变量
'''
print(sys.path)
'''
 查看当前路径
 增加自定义函数文件的路径，到文件夹位置，路径前面不能少了r
 sys.path:返回模块的搜索路径，初始化时使用PYTHONPATH环境变量的值
 例如sys.path.append(r"E:\python\workspace\pythonDemo1")
'''
sys.path.append("..")
'''
 这代表添加当前路径的上一级目录(父目录)
 再引入文件并调用函数
'''
from utils.similarity import calEuclidDistanceMatrix
from utils.knn import myKNN
from utils.laplacian import calLaplacianMatrix
from utils.dataloader import genTwoCircles
from utils.ploter import plot
from sklearn.cluster import KMeans
import numpy as np

'''
 from .A import B 导入A模块中的B函数或变量
 import A as a 导入A模块别名a
'''

np.random.seed(1)
'''
 seed( ) 用于指定随机数生成时所用算法开始的整数值。
 1.如果使用相同的seed( )值，则每次生成的随即数都相同；
 2.如果不设置这个值，则系统根据时间来自己选择这个值，
   此时每次生成的随机数因时间差异而不同。
 3.设置的seed()值仅一次有效
'''

data, label = genTwoCircles(n_samples=500)
# 返回data(生成的样本)；label(每个样本的类成员的整数标签0或1)

Similarity = calEuclidDistanceMatrix(data)
# 返回Similarity(样本距离矩阵)N*N

Adjacent = myKNN(Similarity, k=10)
# 返回A(K邻近矩阵)N*N，将距离转为相似度，K邻近有值，其余为0
Laplacian = calLaplacianMatrix(Adjacent)
# Laplacian:返回拉普拉斯算子运算D^(-1/2) L D^(-1/2)
x, V = np.linalg.eig(Laplacian)
# 计算方形矩阵Laplacian的特征值和特征向量
# x多个特征值组成的一个矢量
# V多个特征向量组成的一个矩阵。
# 每一个特征向量都被归一化了。
# 第i列的特征向量v[:,i]对应第i个特征值x[i]。
x = zip(x, range(len(x)))
# 特征值与序号组成列表
x = sorted(x, key=lambda x: x[0])
# 按列表的第一个元素(特征值)升序排列
H = np.vstack([V[:, i] for (v, i) in x[:500]]).T
# 取最小的500个特征值对应的特征行向量
# 按垂直方向（行顺序）堆叠数组构成一个新的数组,然后转置
sp_kmeans = KMeans(n_clusters=2).fit(H)
# 使用H训练KMeans，聚类为2簇
pure_kmeans = KMeans(n_clusters=2).fit(data)
# 使用原始数据训练KMeans，聚类为2簇
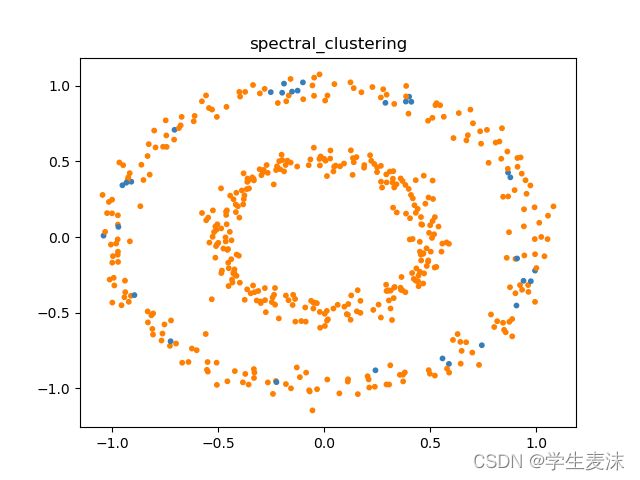
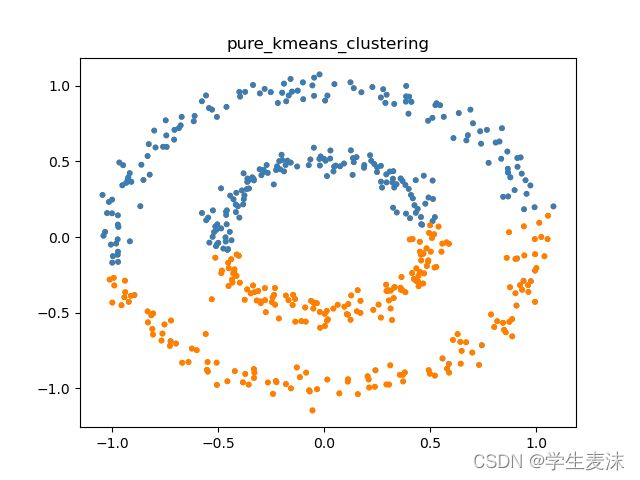
name = ['spectral_clustering','pure_kmeans_clustering']
plot(data, sp_kmeans.labels_, name[0])
plot(data, pure_kmeans.labels_, name[1])
# 画图进行比较

 6.画图（utils/ploter.py ）

from matplotlib import pyplot as plt
from itertools import cycle, islice
import numpy as np
import sys

from matplotlib.pyplot import title

def plot(X, y, title):
    sys.path.append("..")
    colors = np.array(list(islice(
        cycle(['#377eb8', '#ff7f00', '#4daf4a', '#f781bf', '#a65628', '#984ea3', '#999999', '#e41a1c', '#dede00']),
        int(max(y) + 1))))
    plt.title(title)
    plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y])
    plt.savefig("./utils/figures/"+str(title)+".png")

7.结果图

 

 （二）使用sklearn.cluster.SpectralClustering

谱聚类Spectral clustering(SC) – 数据常青藤 (dataivy.cn)https://www.dataivy.cn/blog/%E8%B0%B1%E8%81%9A%E7%B1%BBspectral-clustering/

from sklearn.cluster import SpectralClustering
gamma =0.001
#初始化gamma，也可以加入循环，找最好值
clusterlabel = []
#初始化分组
max = 0
#保存最好的分组
for k in range(2,10):
    #分K组
    for j in range(1,20):
    #j邻居数
      clustering = SpectralClustering(assign_labels="discretize",random_state=0,n_neighbors=j,n_clusters=k,gamma=gamma).fit(X)
      # X：你的数据
      if  metrics.calinski_harabasz_score(X, clustering.labels_) >= max:
        max = metrics.calinski_harabasz_score(X, clustering.labels_)
        clusterlabel = clustering.labels_
        print("n_clusters:", k)
        print("n_neighbors:", j)
        print("Calinski-Harabasz Score:", metrics.calinski_harabasz_score(X, clustering.labels_))
        print('clustering.labels_:', clusterlabel)