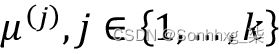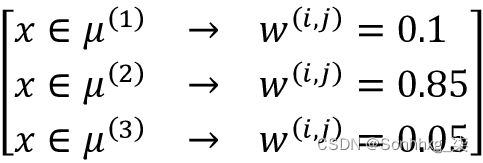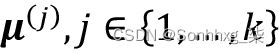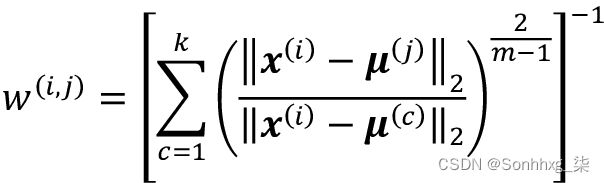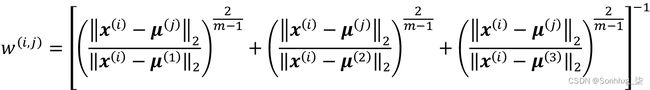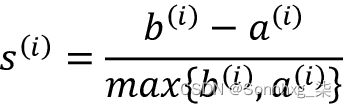【ML】使用未标记数据 - 聚类分析

   大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流

个人主页－Sonhhxg_柒的博客_CSDN博客 

欢迎各位→点赞 + 收藏⭐️ + 留言​

系列专栏 - 机器学习【ML】 自然语言处理【NLP】  深度学习【DL】

​

 foreword

✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

如果你对这个系列感兴趣的话，可以关注订阅哟

 在前面的章节中，我们使用监督学习技术来构建机器学习模型，使用的数据已经知道答案——类标签已经在我们的训练数据中可用。在本章中，我们将切换齿轮并探索聚类分析，这是一类无监督学习技术，使我们能够发现数据中我们预先不知道正确答案的隐藏结构。聚类的目标是在数据中找到一个自然的分组，使得同一聚类中的项目彼此之间的相似性高于不同聚类中的项目。

鉴于其探索性，聚类是一个令人兴奋的话题，在本章中，您将了解以下概念，这些概念可以帮助我们将数据组织成有意义的结构：

• 使用流行的k-means算法查找相似中心
• 采用自下而上的方法构建层次聚类树
• 使用基于密度的聚类方法识别任意形状的对象

使用 k-means 按相似性对对象进行分组

在本节中，我们将了解最受欢迎的之一聚类算法，k-means，在学术界和工业界都广泛使用。聚类（或聚类分析）是一种使我们能够找到与其他组中的对象相比，彼此之间更相关的相似对象。面向业务的聚类应用示例包括按不同主题对文档、音乐和电影进行分组，或者根据共同的购买行为寻找具有相似兴趣的客户作为推荐引擎的基础。

使用 scikit-learn 进行 k 均值聚类

稍后您将看到，k-means算法非常容易实现，但与其他聚类算法相比，它的计算效率也非常高，这可能解释了它的受欢迎程度。这k-means算法属于基于原型的聚类类别。

我们将讨论另外两类聚类，层次和基于密度的聚类，本章后面。

基于原型的聚类意味着每个聚类都由一个原型表示，原型通常是具有连续特征的相似点的质心（平均值），或在分类特征的情况下，中心点（最具代表性或最小化与属于特定集群的所有其他点的距离的点）。虽然 k-means 非常擅长识别具有球形形状的聚类，但这种聚类算法的缺点之一是我们必须先验地指定聚类的数量k。An inappropriate choice for k can result in poor clustering performance. 在本章后面，我们将讨论肘法_和轮廓图，它们是评估聚类质量的有用技术，可帮助我们确定最佳聚类数k。

虽然 k-means 聚类可以应用于更高维度的数据，但我们将使用简单的二维数据集来演示以下示例以进行可视化：

from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=150,
                  n_features=2,
                  centers=3,
                  cluster_std=0.5,
                  shuffle=True,
                  random_state=0)
import matplotlib.pyplot as plt
plt.scatter(X[:, 0],
            X[:, 1],
            c='white',
            marker='o',
            edgecolor='black',
            s=50)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid()
plt.tight_layout()
plt.show()

这我们刚刚创建的数据集由 150 个随机生成的点大致分为三个密度较高的区域，通过二维散点图可视化：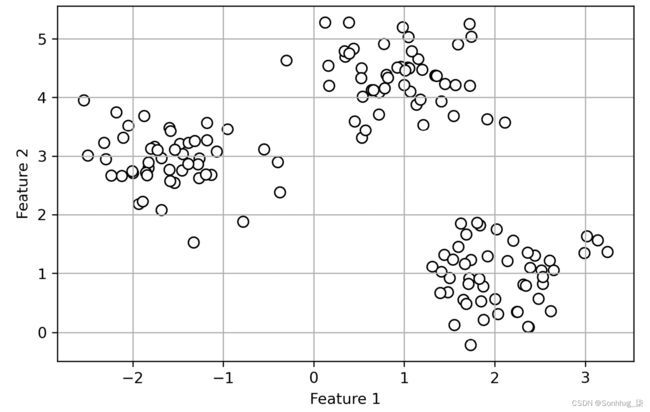

                                                图 10.1：我们未标记数据集的散点图

在聚类的实际应用中，我们没有关于这些示例的任何真实类别信息（作为经验证据而不是推理提供的信息）；如果我们被赋予类别标签，那么这个任务将属于监督学习的范畴。因此，我们的目标是根据样本的特征相似性对样本进行分组，这可以使用 k-means 算法来实现，总结为以下四个步骤：

1. 从示例中随机选择k个质心作为初始聚类中心
2. 将每个示例分配给最近的质心，
3. 将质心移动到分配给它的示例的中心
4. 重复步骤 2和3，直到集群分配不改变或达到用户定义的容差或最大迭代次数

现在，下一个问题是，我们如何衡量对象之间的相似性？我们可以将相似度定义为距离的反义词，对具有连续特征的样本进行聚类的常用距离是两点x和y之间的平方欧几里得距离，在m维空间中：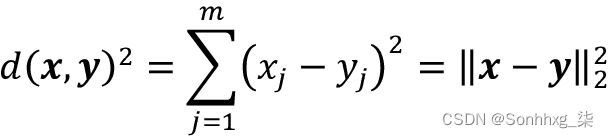

 请注意，在前面的等式中，索引j指的是示例输入x和y的第j个维度（特征列）。在本节的其余部分中，我们将使用上标i和j分别表示示例（数据记录）的索引和集群索引。

基于这个欧几里得距离度量，我们可以将 k-means 算法描述为一个简单的优化问题，一个最小化的迭代方法簇内误差平方和( SSE )，有时也称为簇惯性：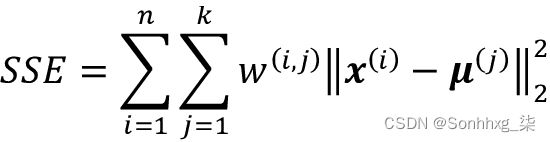

这里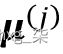，是集群j的代表点（质心）。w ( i ,  j )  = 1 如果示例x ( i )在集群j中，否则为 0。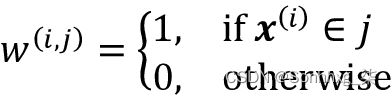

 既然你已经学会了KMeans简单的 k-means 算法是如何工作的，让我们使用scikit-learncluster模块中的类将它应用到我们的示例数据集：

from sklearn.cluster import KMeans
km = KMeans(n_clusters=3,
            init='random',
            n_init=10,
            max_iter=300,
            tol=1e-04,
            random_state=0)
y_km = km.fit_predict(X)

使用前面的代码，我们将所需集群的数量设置为3; 必须先验地指定簇的数量是 k-means 的限制之一。我们设置n_init=10独立运行 k-means 聚类算法 10 次，使用不同的随机质心选择最终模型作为 SSE 最低的模型。通过max_iter参数，我们指定每次运行的最大迭代次数（此处为300）。请注意，如果在达到最大迭代次数之前收敛，scikit-learn 中的 k-means 实现会提前停止。但是，k-means 可能无法在特定运行中达到收敛，如果我们为max_iter. 处理收敛问题的一种方法是为 选择更大的值tol，这是一个参数，用于控制关于集群内 SSE 变化的容差，以声明收敛。在前面的代码中，我们选择了1e-04(=0.0001) 的容差。

一个问题k-means 是一个或多个簇可以是空的。笔记k-medoids 或模糊 C-means 不存在这个问题，我们将在本节后面讨论这种算法。然而，这个问题在 scikit-learn 的当前 k-means 实现中得到了解决。如果一个簇是空的，算法将搜索离空簇的质心最远的例子。然后，它将重新分配质心到这个最远的点。

特征缩放

当我们使用欧几里得距离度量将 k-means 应用于真实世界的数据时，我们希望确保在相同的尺度上测量特征，并在必要时应用 z-score 标准化或 min-max 缩放。

预测了集群标签，y_km并讨论了 k-means 算法的一些挑战，现在让我们可视化 k-means 在数据集中识别的集群以及集群质心。这些存储在cluster_centers_拟合KMeans对象的属性下：

plt.scatter(X[y_km == 0, 0],
            X[y_km == 0, 1],
            s=50, c='lightgreen',
            marker='s', edgecolor='black',
            label='Cluster 1')
plt.scatter(X[y_km == 1, 0],
            X[y_km == 1, 1],
            s=50, c='orange',
            marker='o', edgecolor='black',
            label='Cluster 2')
plt.scatter(X[y_km == 2, 0],
            X[y_km == 2, 1],
            s=50, c='lightblue',
            marker='v', edgecolor='black',
            label='Cluster 3')
plt.scatter(km.cluster_centers_[:, 0],
            km.cluster_centers_[:, 1],
            s=250, marker='*',
            c='red', edgecolor='black',
            label='Centroids')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(scatterpoints=1)
plt.grid()
plt.tight_layout()
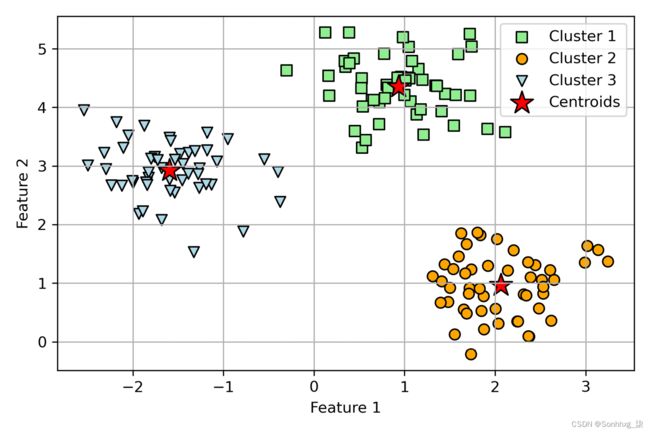
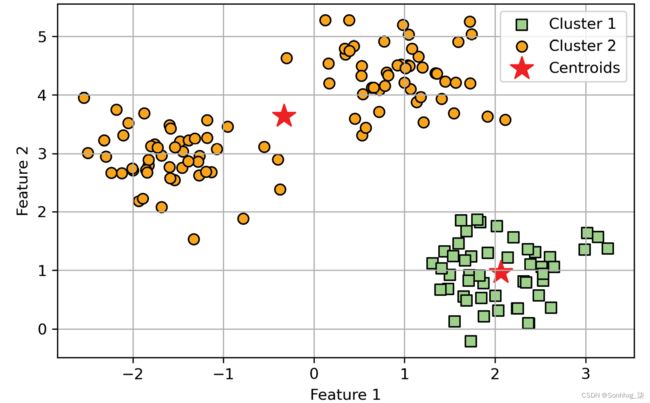
plt.show()

在图 10.2中，你可以看到 k-means 将三个质心放在每个球体的中心，给定这个数据集，这看起来像是一个合理的分组：

 

图 10.2：k-means 聚类及其质心

尽管 k-means 在这个玩具数据集上运行良好，但我们仍然存在必须先验地指定聚类数量k的缺点。在实际应用中，要选择的集群数量可能并不总是那么明显，尤其是当我们使用无法可视化的高维数据集时。k-means 的其他属性是集群不重叠且不分层，我们还假设每个集群中至少有一个项目。在本章后面，我们将遇到不同类型的聚类算法，分层聚类和基于密度的聚类。这两种算法都不需要我们预先指定集群的数量或在我们的数据集中假设球形结构。

在下一小节中，我们将介绍经典 k-means 算法的一个流行变体，称为k-means++。虽然它没有解决上一段中讨论的 k-means 的那些假设和缺点，但它可以通过更巧妙地对初始聚类中心进行播种来大大改善聚类结果。

使用 k-means++ 放置初始集群质心的更智能方法

到目前为止，我们已经讨论了经典的 k-means 算法，它使用放置初始质心的随机种子，如果初始质心选择不当，有时会导致聚类不良或收敛缓慢。解决此问题的一种方法是在数据集上多次运行 k-means 算法，并根据 SSE 选择性能最佳的模型。

另一种策略是通过 k-means++ 算法将初始质心彼此远离，这比经典的 k-means 得到更好和更一致的结果（k-means++: The Benefits of Careful Seeding by D. Arthur and S . Vassilvitskii在第十八届 ACM-SIAM 离散算法年度研讨会论文集上，第 1027-1035 页。工业和应用数学学会，2007）。

k-means++中的初始化可以总结如下：

1. 初始化一个空集M以存储被选择的k个质心。
2. 从输入示例中随机选择第一个质心 ,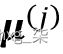并将其分配给M。
3. 对于每个不在M中的示例x ( i ) ，找到到M中任何质心的最小平方距离d ( x ( i ) ,  M ) 2。
4. 要随机选择下一个质心 ，请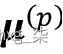使用等于 的加权概率分布。例如，我们收集数组中的所有点并选择加权随机抽样，这样平方距离越大，一个点被选为质心的可能性就越大。
5. 重复步骤 3和4，直到选择k个质心。
6. 继续使用经典的 k-means 算法。

要将 k-means++ 与 scikit-learn 的KMeans对象一起使用，我们只需将init参数设置为'k-means++'. 实际上，'k-means++'是参数的默认参数init，在实践中强烈建议使用。我们在前面的例子中没有使用它的唯一原因是不要一次引入太多的概念。本节剩下的关于 k-means 的内容将使用 k-means++，但你是鼓励尝试更多地使用两种不同的方法（经典 k-means viainit='random'与 k-means++ via init='k-means++'）来放置初始集群质心。

硬聚类与软聚类

硬聚类描述一组算法，其中数据集中的每个示例都被分配给一个集群，如 k-means 和 k-means++ 算法我们在本章前面讨论过。相比之下，软聚类算法（有时也称为模糊聚类）将示例分配给一个或多个聚类。软聚类的一个流行例子是模糊 C 均值( FCM ) 算法（也称为软 k 均值或模糊 k 均值）。最初的想法可以追溯到 1970 年代，当时 Joseph C. Dunn提出了模糊聚类的早期版本以改进 k-means（ISODATA 过程的模糊相对及其在检测紧凑的分离良好的聚类中的应用，1973 年）。差不多十年后，James C. Bedzek 发表了他关于改进模糊聚类算法的工作，该算法现在被称为 FCM 算法（带模糊目标函数算法的模式识别，Springer Science+Business Media，2013）。

FCM 过程与 k-means 非常相似。然而，我们用属于每个簇的每个点的概率替换了硬簇分配。在 k-means 中，我们可以用二进制值的稀疏向量表示示例x的集群成员资格：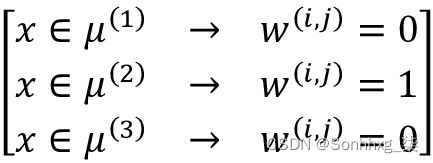

 此处，值为 1 的索引位置表示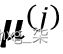该示例分配给的簇质心 （假设k  = 3, ）。相反，FCM 中的成员向量可以表示如下：

 

在这里，每个值都落在 [0, 1] 范围内，并表示相应聚类质心的成员资格概率。给定示例的成员资格之和等于 1。与 k-means 算法一样，我们可以将 FCM 算法总结为四个关键步骤：

1. 指定k个质心的数量并为每个点随机分配集群成员资格
2. 计算集群质心，
3. 更新每个点的集群成员资格
4. 重复步骤 2和3，直到隶属系数不变或达到用户定义的容差或最大迭代次数

FCM 的目标函数（我们将其缩写为J m）看起来与我们在 k-means 中最小化的集群内 SSE 非常相似：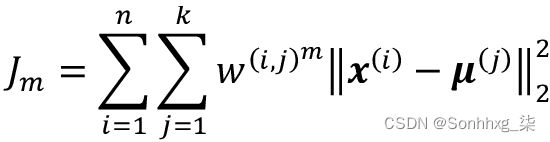

但是，请注意，成员指标w ( i ,  j )不是 k-means ( ) 中的二进制值，而是表示集群成员概率 ( ) 的实数值。您可能还注意到我们在w ( i ,  j )中添加了一个附加指数；指数m , 任意大于或等于一的数字（通常m  = 2），就是所谓的模糊系数（或简称为fuzzifier），它控制着模糊的程度。

m的值越大，集群成员w ( i ,  j )变得越小，这会导致集群更加模糊。集群成员概率本身计算如下：

例如，如果我们选择三个集群中心，如前面的 k-means 示例，我们可以计算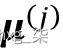属于集群的成员资格如下：

 

一个簇本身的中心 ,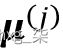计算为所有实例的平均值，每个实例属于该簇 ( ) 的程度加权：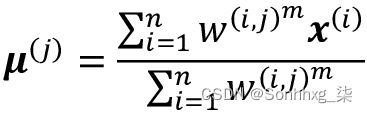

 仅通过查看计算集群成员的方程，我们可以说 FCM 中的每次迭代都比 k-means 中的迭代更昂贵。另一方面，FCM 通常需要更少的迭代来达到收敛。然而，在实践中发现，k-means 和 FCM 都产生非常相似的聚类输出，如一项研究（S. Ghosh和SK Dubey的 K-means 和模糊 C-Means 算法的比较分析，IJACSA , 4: 35–38, 2013)。遗憾的是，目前 scikit-learn 中并没有实现 FCM 算法，但是有兴趣的读者可以从scikit-fuzzy 包，可在GitHub - scikit-fuzzy/scikit-fuzzy: Fuzzy Logic SciKit (Toolkit for SciPy)获得。

使用肘法寻找最佳聚类数

无监督学习的主要挑战之一是我们不知道明确的答案。我们的数据集中没有真实类标签，无法应用我们在第 6 章中使用的技术，学习模型评估和超参数调整的最佳实践，来评估监督模型的性能。因此，为了量化聚类的质量，我们需要使用内在指标——例如集群内 SSE（失真）——来比较不同 k-means 聚类模型的性能。

方便的是，我们不当我们使用 scikit-learn 时，需要显式计算集群内 SSE，因为在拟合模型inertia_后它已经可以通过属性访问：KMeans

print(f'Distortion: {km.inertia_:.2f}')
# Distortion: 72.48

基于集群内 SSE，我们可以使用图形工具，即所谓的肘法，来估计给定任务的最佳集群数k 。我们可以说，如果k增加，失真就会减少。这是因为示例将更接近它们分配到的质心。肘部方法背后的想法是确定k的值，其中失真开始增加最快，如果我们绘制不同k值的失真，这将变得更加清晰：

distortions = []
for i in range(1, 11):
    km = KMeans(n_clusters=i,
                init='k-means++',
                n_init=10,
                max_iter=300,
                random_state=0)
    km.fit(X)
    distortions.append(km.inertia_)
plt.plot(range(1,11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.tight_layout()
plt.show()

尽你所能如图 10.3 所示，肘部位于k =  3，因此这支持了k  = 3 对于这个数据集确实是一个不错的选择：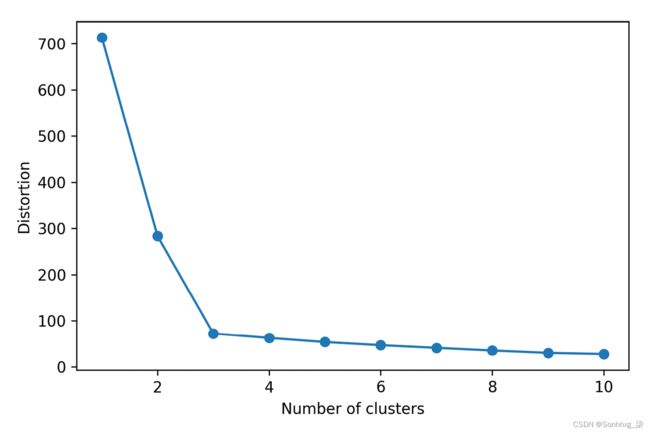

图 10.3：使用肘法寻找最佳聚类数

通过轮廓图量化聚类的质量

评估产品质量的另一个内在指标聚类是轮廓分析，它也可以应用于除 k-means 之外的聚类算法，我们将在本章后面讨论。轮廓分析可用作图形工具来绘制衡量集群中示例的紧密程度。计算轮廓系数我们数据集中的一个例子，我们可以应用以下三个步骤：

1. 计算簇内聚力a ( i )作为示例x ( i )与同一簇中所有其他点之间的平均距离。
2. 计算与下一个最近的聚类的聚类分离b ( i )作为示例x ( i )与最近聚类中的所有示例之间的平均距离。
3. 将轮廓s ( i )计算为集群凝聚力和分离度之间的差异除以两者中的较大者，如下所示：

   

轮廓系数在–1到1的范围内。根据前面的等式，我们可以看到，如果聚类分离和内聚相等（b （i ）  =  a （i ）），则轮廓系数为0。此外，如果b ( i )  >>  a ( i )，我们会接近理想的轮廓系数 1 ，因为b ( i )量化了一个示例与其他聚类的不同程度，而a ( i )告诉我们它的相似程度到它自己的集群中的其他示例。

剪影系数可silhouette_samples从 scikit-learn 的metric模块中获得，并且silhouette_scores可以选择导入该函数以方便使用。该silhouette_scores函数计算所有示例的平均轮廓系数，相当于numpy.mean(silhouette_samples(...)). 通过执行以下代码，我们现在将为k  = 3 的 k 均值聚类创建轮廓系数图：

km = KMeans(n_clusters=3,
            init='k-means++',
            n_init=10,
            max_iter=300,
            tol=1e-04,
            random_state=0)
y_km = km.fit_predict(X)
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(
    X, y_km, metric='euclidean'
)
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
    c_silhouette_vals = silhouette_vals[y_km == c]
    c_silhouette_vals.sort()
    y_ax_upper += len(c_silhouette_vals)
    color = cm.jet(float(i) / n_clusters)
    plt.barh(range(y_ax_lower, y_ax_upper),
             c_silhouette_vals,
             height=1.0,
             edgecolor='none',
             color=color)
    yticks.append((y_ax_lower + y_ax_upper) / 2.)
    y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg,
            color="red",
            linestyle="--")
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
plt.show()

通过视觉检查轮廓图，我们可以快速检查不同聚类的大小并识别包含异常值的聚类：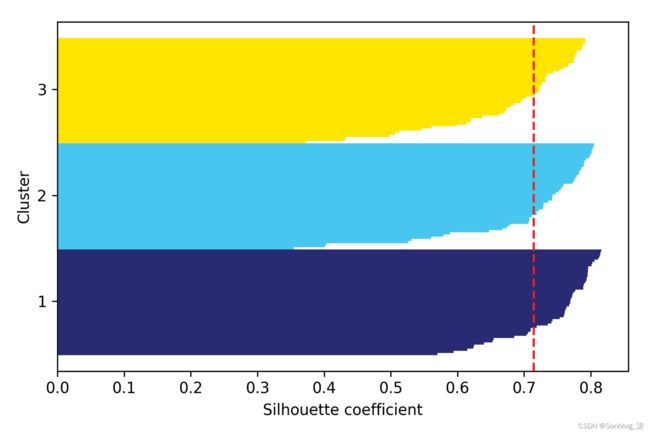

                                        图 10.4：一个很好的聚类示例的轮廓图

但是，正如您在前面的轮廓图中看到的那样，轮廓系数并不接近 0，并且与平均轮廓分数的距离大致相等，在这种情况下，平均轮廓分数是良好聚类的指标。此外，为了总结我们聚类的优点，我们在图中添加了平均轮廓系数（虚线）。

看看是什么轮廓图看起来像是一个相对较差的聚类，让我们用只有两个质心的 k-means 算法播种：

km = KMeans(n_clusters=2,
            init='k-means++',
            n_init=10,
            max_iter=300,
            tol=1e-04,
            random_state=0)
y_km = km.fit_predict(X)
plt.scatter(X[y_km == 0, 0],
            X[y_km == 0, 1],
            s=50, c='lightgreen',
            edgecolor='black',
            marker='s',
            label='Cluster 1')
plt.scatter(X[y_km == 1, 0],
            X[y_km == 1, 1],
            s=50,
            c='orange',
            edgecolor='black',
            marker='o',
            label='Cluster 2')
plt.scatter(km.cluster_centers_[:, 0],
            km.cluster_centers_[:, 1],
            s=250,
            marker='*',
            c='red',
            label='Centroids')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()

正如您在图 10.5中看到的，其中一个质心位于输入数据的三个球形分组中的两个之间。

虽然聚类看起来并不完全糟糕，它是次优的：

                                                图 10.5：聚类的次优示例

铭记于心在现实世界的问题中，我们通常没有在二维散点图中可视化数据集的奢侈，因为我们通常使用更高维度的数据。因此，接下来，我们将创建轮廓图来评估结果：

cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(
    X, y_km, metric='euclidean'
)
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
    c_silhouette_vals = silhouette_vals[y_km == c]
    c_silhouette_vals.sort()
    y_ax_upper += len(c_silhouette_vals)
    color = cm.jet(float(i) / n_clusters)
    plt.barh(range(y_ax_lower, y_ax_upper),
             c_silhouette_vals,
             height=1.0,
             edgecolor='none',
             color=color)
    yticks.append((y_ax_lower + y_ax_upper) / 2.)
    y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--")
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
plt.show()

正如您在图 10.6中看到的，轮廓现在具有明显不同的长度和宽度，即相对较差或至少次优聚类的证据：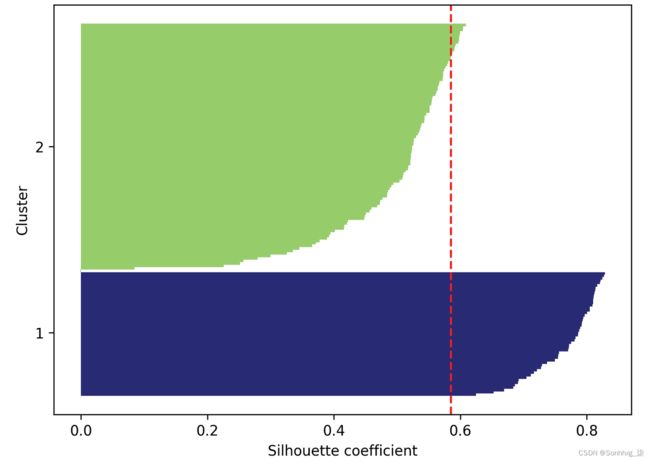

                                                 图 10.6：次优聚类示例的轮廓图

现在，在我们很好地理解了聚类的工作原理之后，下一节将介绍层次聚类作为 k-means 的替代方法。

将集群组织为层次树

在本节中，我们将研究基于原型的聚类的另一种方法：层次聚类。优势之一层次聚类算法的特点是它允许我们绘制树状图（二进制层次聚类的可视化），它可以帮助解释结果创建有意义的分类法。其他这种分层方法的优点是我们不需要预先指定集群的数量。

分层的两种主要方法聚类是凝聚和分裂的层次聚类。在分裂层次聚类中，我们从一个聚类开始包含完整的数据集，我们迭代地将集群拆分为更小的集群，直到每个集群只包含一个示例。在本节中，我们将重点关注采用相反方法的凝聚聚类。我们从每个示例开始作为一个单独的集群，然后合并最近的集群对，直到只剩下一个集群。

以自下而上的方式对集群进行分组

两个标准凝聚层次聚类算法有单联动和全联动。使用单链接，我们计算每对集群中最相似成员之间的距离，并合并最相似成员之间距离最小的两个集群。完整的联动方法类似于单链接，但我们不是比较每对集群中最相似的成员，而是比较最不相似的成员来执行合并。如图 10.7所示：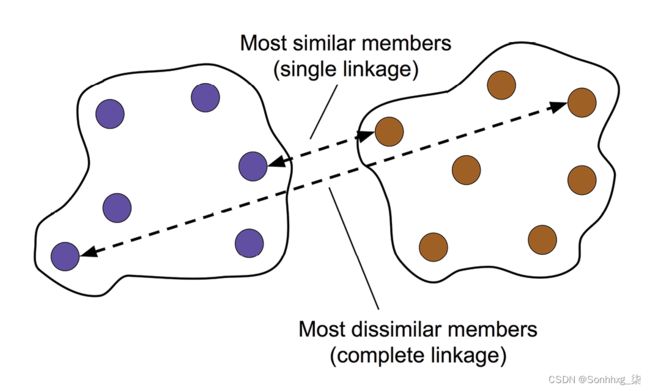

                                                         图 10.7：完整的链接方法

其他类型的联系

其他常用的凝聚层次聚类算法包括平均链接和沃德链接。在平均链接中，我们基于最小值合并集群对两个集群中所有组成员之间的平均距离。在 Ward 的链接中，导致集群内 SSE 总增长最小的两个集群被合并。

在本节中，我们将重点关注使用完整链接方法的凝聚聚类。层次完全链接聚类是一个迭代过程，可以概括为以下步骤：

1. 计算所有示例的成对距离矩阵。
2. 将每个数据点表示为一个单例集群。
3. 根据最不相似（远距离）成员之间的距离合并两个最近的集群。
4. 更新集群链接矩阵。
5. 重复步骤 2-4，直到剩下一个集群。

接下来，我们将讨论如何计算距离矩阵（步骤 1）。但首先，让我们生成一个随机数据样本来处理。行代表不同的观察结果（ID 0-4），列是这些示例的不同特征（ X、Y、 ）：Z

import pandas as pd
import numpy as np
np.random.seed(123)
variables = ['X', 'Y', 'Z']
labels = ['ID_0', 'ID_1', 'ID_2', 'ID_3', 'ID_4']
X = np.random.random_sample([5, 3])*10
df = pd.DataFrame(X, columns=variables, index=labels)
df

执行上述操作后代码，我们现在应该看到以下DataFrame包含随机生成的示例：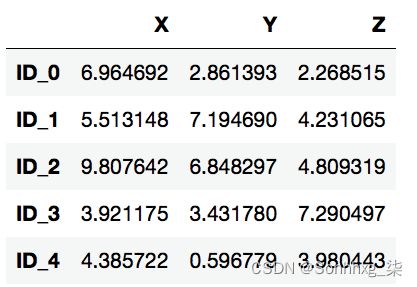

                 图 10.8：随机生成的数据样本

对距离矩阵执行层次聚类

计算距离矩阵作为输入层次聚类算法，我们将使用pdistSciPyspatial.distance子模块中的函数：

from scipy.spatial.distance import pdist, squareform
row_dist = pd.DataFrame(squareform(
                        pdist(df, metric='euclidean')),
                        columns=labels, index=labels)
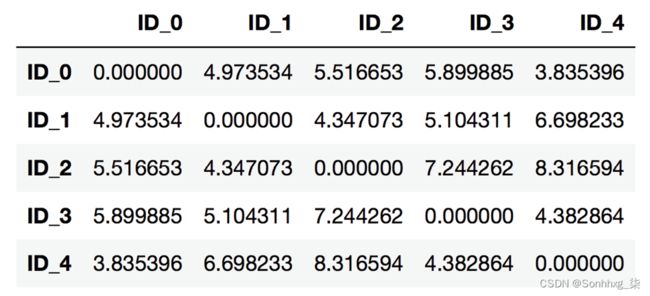
row_dist

使用前面的代码，我们根据特征X、Y和计算数据集中每对输入示例之间的欧几里得距离Z。

我们提供了压缩距离矩阵（由返回）作为函数的pdist输入，squareform以创建成对距离的对称矩阵，如下所示：.

                                                 图 10.9：我们计算的数据的成对距离

接下来，我们将应用完整的链接linkage使用SciPy子模块中的函数聚集到我们的集群，该函数cluster.hierarchy返回一个所谓的联动矩阵。

不过，在我们调用linkage函数之前，让我们仔细看一下函数文档：

>>> from scipy.cluster.hierarchy import linkage
>>> help(linkage)
[...]
Parameters:
  y : ndarray
    A condensed or redundant distance matrix. A condensed
    distance matrix is a flat array containing the upper
    triangular of the distance matrix. This is the form
    that pdist returns. Alternatively, a collection of m
    observation vectors in n dimensions may be passed as
    an m by n array.
  
  method : str, optional
    The linkage algorithm to use. See the Linkage Methods
    section below for full descriptions.
  
  metric : str, optional
    The distance metric to use. See the distance.pdist
    function for a list of valid distance metrics.
  
  Returns:
  Z : ndarray
    The hierarchical clustering encoded as a linkage matrix.
[...]

根据函数描述，我们了解到我们可以使用函数的压缩距离矩阵（上三角）pdist作为输入属性。或者，我们也可以提供初始数据数组和使用'euclidean'中作为函数参数的度量linkage。但是，我们不应该使用squareform我们之前定义的距离矩阵，因为它会产生与预期不同的距离值。总结一下，这里列出了三种可能的情况：

• 不正确的方法：使用squareform如下代码片段所示的距离矩阵会导致不正确的结果：

  row_clusters = linkage(row_dist,
                         method='complete',
                         metric='euclidean')

• 正确的方法：使用如下代码示例中所示的压缩距离矩阵会产生正确的链接矩阵：

  row_clusters = linkage(pdist(df, metric='euclidean'),
                         method='complete')

• 正确的方法：使用如下代码片段所示的完整输入示例矩阵（所谓的设计矩阵）也可以得出与上述方法类似的正确链接矩阵：

  row_clusters = linkage(df.values,
                         method='complete',
                         metric='euclidean')

要仔细查看聚类结果，我们可以将这些结果转换为 pandas DataFrame（最好在 Jupyter notebook 中查看），如下所示：

pd.DataFrame(row_clusters,
             columns=['row label 1',
                      'row label 2',
                      'distance',
                      'no. of items in clust.'],
             index=[f'cluster {(i + 1)}' for i in
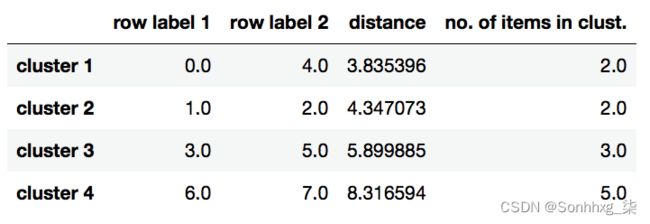
                    range(row_clusters.shape[0])])

如图 10.10所示，链接矩阵由几行组成，每一行代表一个合并。第一和第二列表示每个中最不同的成员簇，第三列报告这些成员之间的距离。

最后一列返回每个集群中的成员数：

图 10.10：链接矩阵

现在我们已经计算了链接矩阵，我们可以以树状图的形式可视化结果：

from scipy.cluster.hierarchy import dendrogram
# make dendrogram black (part 1/2)
# from scipy.cluster.hierarchy import set_link_color_palette
# set_link_color_palette(['black'])
row_dendr = dendrogram(
    row_clusters,
    labels=labels,
    # make dendrogram black (part 2/2)
    # color_threshold=np.inf
)
plt.tight_layout()
plt.ylabel('Euclidean distance')
plt.show()

如果您正在执行前面的代码或阅读本书的电子书版本，您会注意到生成的树状图中的分支以不同的颜色显示。颜色方案源自 Matplotlib 颜色列表，这些颜色循环用于树状图中的距离阈值。例如，要以黑色显示树状图，您可以取消注释相应的部分插入在前面的代码中：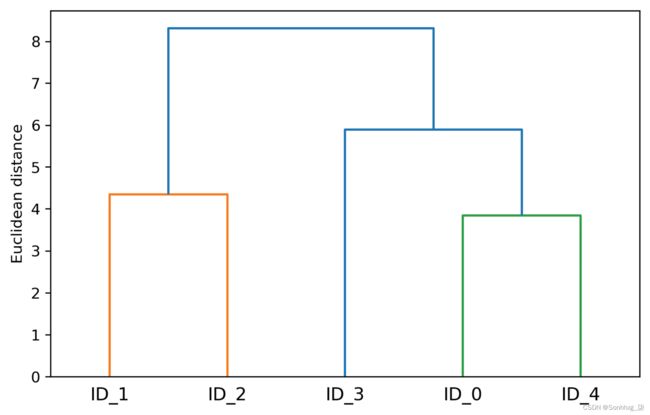

图 10.11：我们数据的树状图

这样的树状图总结了凝聚层次聚类过程中形成的不同聚类；例如，您可以看到示例ID_0和ID_4，然后是ID_1和ID_2，是基于欧几里得距离度量的最相似的示例。

将树状图附加到热图

在实际应用中，层次聚类树状图经常与热图结合使用，它允许我们表示数据数组或矩阵中的各个值包含我们的带有颜色代码的训练示例。在本节中，我们将讨论如何将树状图附加到热图中并相应地对热图中的行进行排序。

但是，附加一个树状图到热图可能有点棘手，所以让我们一步一步地完成这个过程：

1. 我们创建一个新figure对象，并通过属性定义树状图的x轴位置、y轴位置、宽度和高度。add_axes此外，我们将树状图逆时针旋转 90 度。代码如下：

   fig = plt.figure(figsize=(8, 8), facecolor='white')
   axd = fig.add_axes([0.09, 0.1, 0.2, 0.6])
   row_dendr = dendrogram(row_clusters,
                          orientation='left')
   # note: for matplotlib < v1.5.1, please use
   # orientation='right'

2. DataFrame接下来，我们根据可以从dendrogram对象（本质上是一个 Python 字典）通过leaves键访问的聚类标签对初始数据进行重新排序。代码如下：

   df_rowclust = df.iloc[row_dendr['leaves'][::-1]]

3. 现在，我们从重新排序的图像中构建热图，并将其放置DataFrame在树状图旁边：

   axm = fig.add_axes([0.23, 0.1, 0.6, 0.6])
   cax = axm.matshow(df_rowclust,
                     interpolation='nearest',
                     cmap='hot_r')

4. 最后，我们通过移除轴刻度并隐藏轴刺来修改树状图的美感。此外，我们添加了一个颜色条并将特征和数据记录名称分别分配给x和y轴刻度标签：

   axd.set_xticks([])
   axd.set_yticks([])
   for i in axd.spines.values():
       i.set_visible(False)
   fig.colorbar(cax)
   axm.set_xticklabels([''] + list(df_rowclust.columns))
   axm.set_yticklabels([''] + list(df_rowclust.index))
   plt.show()

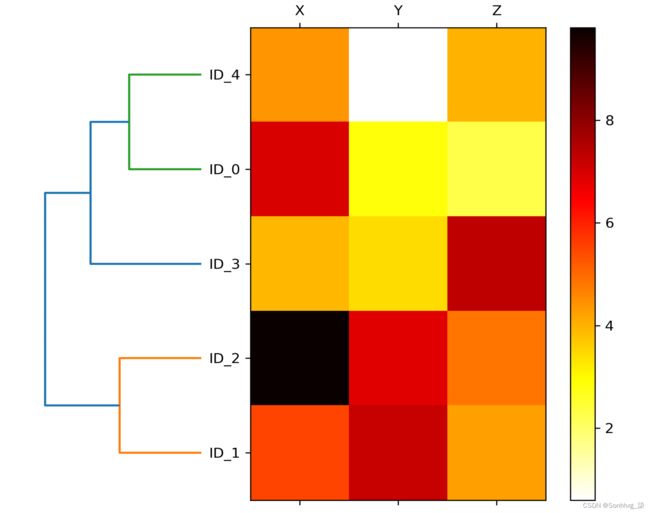
完成上述步骤后，应显示热图并附上树状图：

图 10.12：我们数据的热图和树状图

如您所见，热图反映了聚类树状图中的示例。除了简单的树状图之外，热图中每个示例和特征的颜色编码值还为我们提供了数据集的一个很好的摘要。

通过 scikit-learn 应用凝聚聚类

在上一小节中，您了解了如何使用 SciPy 执行凝聚层次聚类。但是，也有一个AgglomerativeClustering实现scikit-learn，它允许我们选择我们想要返回的集群数量。如果我们想修剪层次聚类树，这很有用。

通过将n_cluster参数设置为3，我们现在将使用基于欧几里德距离度量的相同完整链接方法将输入示例分为三组：

from sklearn.cluster import AgglomerativeClustering
ac = AgglomerativeClustering(n_clusters=3,
                             affinity='euclidean',
                             linkage='complete')
labels = ac.fit_predict(X)
print(f'Cluster labels: {labels}')
# Cluster labels: [1 0 0 2 1]

查看预测的集群标签，我们可以看到第一个和第五个示例（ID_0和ID_4）被分配到一个集群（标签1），示例ID_1和ID_2被分配到第二个集群（标签0）。该示例ID_3被放入其自己的集群（标签2）中。总体而言，结果与我们在树状图中观察到的结果一致。但是，我们应该注意到，它与and比与andID_3更相似，如图所示ID_4ID_0ID_1ID_2在前面的树状图中；从 scikit-learn 的聚类结果中并不清楚这一点。现在让我们在以下代码片段中重新运行AgglomerativeClusteringusing ：n_cluster=2

ac = AgglomerativeClustering(n_clusters=2,
                             affinity='euclidean',
                             linkage='complete')
labels = ac.fit_predict(X)
print(f'Cluster labels: {labels}')
# Cluster labels: [0 1 1 0 0]

如您所见，在这个修剪后的聚类层次结构中，标签被分配给与和ID_3相同的聚类，正如预期的那样。ID_0ID_4

通过 DBSCAN 定位高密度区域

尽管我们无法在本章中涵盖大量不同的聚类算法，但至少让我们再包含一种聚类方法：基于密度的带噪声应用程序空间聚类（DBSCAN），它不对像 k 这样的球形聚类做出假设-意味着，它也不会将数据集划分为需要手动截止点。顾名思义，基于密度的聚类根据点的密集区域分配聚类标签。在 DBSCAN 中，密度的概念定义为指定半径内的点数。

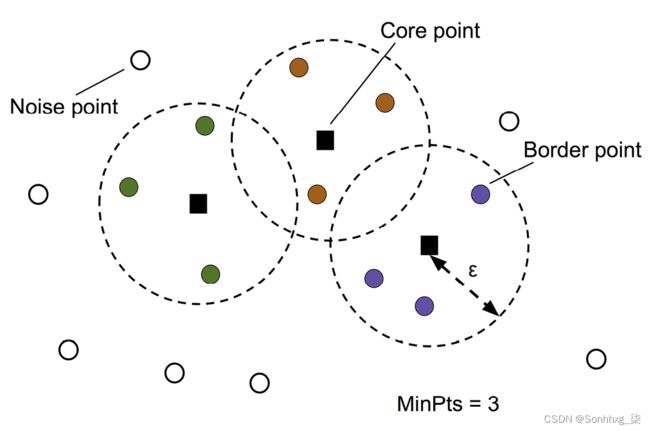
根据 DBSCAN 算法，使用以下标准为每个示例（数据点）分配一个特殊标签：

• 考虑一个点如果至少指定数量 (MinPts) 的相邻点落在指定半径内，则为核心点，
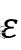
• 边界点是一个点内的邻居比 MinPts 少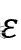，但位于核心点的半径内
• 所有其他点核心点和边界点均不被视为噪声点

在将点标记为核心、边界或噪声之后，DBSCAN 算法可以总结为两个简单的步骤：

1. 形成一个单独的为每个核心点或连接的核心点组聚类。（如果核心点不超过 ，则连接。）
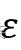2. 将每个边界点分配给其对应核心点的簇。

为了更好地理解 DBSCAN 的结果会是什么样子，在开始实现之前，让我们总结一下我们刚刚学到的关于图 10.13中的核心点、边界点和噪声点的知识：

图 10.13：DBSCAN 的核心、噪声和边界点

使用 DBSCAN 的主要优点之一是它不假设集群具有像 k-means 中的球形。此外，DBSCAN 与 k-means 和层次聚类的不同之处在于，它不一定将每个点分配给一个聚类，但能够去除噪声点。

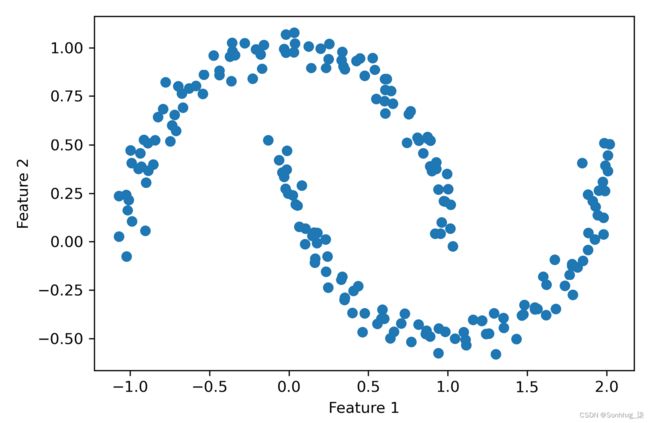
举个更说明性的例子，让我们创建一个新的半月形结构数据集来比较 k-means 聚类、层次聚类和 DBSCAN：

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200,
                  noise=0.05,
                  random_state=0)
plt.scatter(X[:, 0], X[:, 1])
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.tight_layout()
plt.show()

正如您在结果图中看到的那样，有两个可见的半月形组，每个组由 100 个示例（数据点）组成：

图 10.14：两个特征的半月形数据集

我们将从使用开始k-means 算法和完整的链接聚类，以查看之前讨论的聚类算法之一是否可以成功地将半月形识别为单独的聚类。代码如下：

f, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 3))
km = KMeans(n_clusters=2,
            random_state=0)
y_km = km.fit_predict(X)
ax1.scatter(X[y_km == 0, 0],
            X[y_km == 0, 1],
            c='lightblue',
            edgecolor='black',
            marker='o',
            s=40,
            label='cluster 1')
ax1.scatter(X[y_km == 1, 0],
            X[y_km == 1, 1],
            c='red',
            edgecolor='black',
            marker='s',
            s=40,
            label='cluster 2')
ax1.set_title('K-means clustering')
ax1.set_xlabel('Feature 1')
ax1.set_ylabel('Feature 2')
ac = AgglomerativeClustering(n_clusters=2,
                             affinity='euclidean',
                             linkage='complete')
y_ac = ac.fit_predict(X)
ax2.scatter(X[y_ac == 0, 0],
            X[y_ac == 0, 1],
            c='lightblue',
            edgecolor='black',
            marker='o',
            s=40,
            label='Cluster 1')
ax2.scatter(X[y_ac == 1, 0],
            X[y_ac == 1, 1],
            c='red',
            edgecolor='black',
            marker='s',
            s=40,
            label='Cluster 2')
ax2.set_title('Agglomerative clustering')
ax2.set_xlabel('Feature 1')
ax2.set_ylabel('Feature 2')
plt.legend()
plt.tight_layout()
plt.show()

基于可视化聚类结果，我们可以看到 k-means 算法无法将两个聚类分开，而且层次聚类算法也受到了这些复杂形状的挑战：

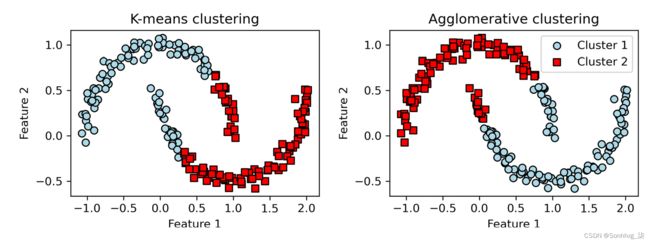图 10.15：半月形数据集上的 k-means 和凝聚聚类

最后，让我们在这个数据集上尝试 DBSCAN 算法，看看它是否可以使用基于密度的方法找到两个半月形簇：

from sklearn.cluster import DBSCAN
db = DBSCAN(eps=0.2,
            min_samples=5,
            metric='euclidean')
y_db = db.fit_predict(X)
plt.scatter(X[y_db == 0, 0],
            X[y_db == 0, 1],
            c='lightblue',
            edgecolor='black',
            marker='o',
            s=40,
            label='Cluster 1')
plt.scatter(X[y_db == 1, 0],
            X[y_db == 1, 1],
            c='red',
            edgecolor='black',
            marker='s',
            s=40,
            label='Cluster 2')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.tight_layout()
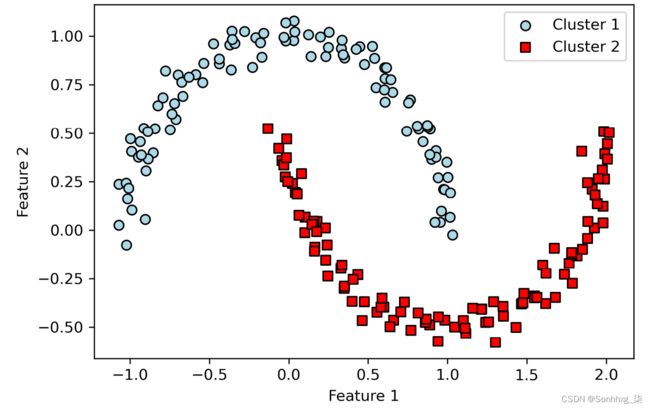
plt.show()

DBSCAN 算法可以成功检测出半月形，这凸显了 DBSCAN 的优势之一——任意形状的聚类数据：

图 10.16：半月形数据集上的 DBSCAN 聚类

然而，我们还应注意 DBSCAN 的一些缺点。随着我们数据集中特征数量的增加——假设训练样本数量固定——维度诅咒的负面影响也在增加。如果我们使用欧几里得距离度量，这尤其是一个问题。然而，维数诅咒的问题并不是 DBSCAN 独有的：它也会影响其他使用欧几里德距离度量的聚类算法，例如 k-means 和层次聚类算法。此外，我们在 DBSCAN 中有两个超参数（MinPts 和）需要优化以产生良好的聚类结果。如果数据集中的密度差异相对较大，则找到 MinPts 的良好组合可能会出现问题。

基于图的聚类

到目前为止，我们已经看到了三种最基本的聚类算法类别：使用 k-means 的基于原型的聚类、凝聚层次聚类和通过 DBSCAN 的基于密度的聚类。但是，还有第四类更高级的聚类算法，我们在本章中没有涉及：基于图的聚类。基于图的聚类家族中最突出的成员可能是谱聚类算法。

尽管谱聚类有许多不同的实现方式，但它们的共同点是它们使用相似度或距离矩阵的特征向量来推导聚类关系。由于谱聚类超出了本书的范围，您可以阅读 Ulrike von Luxburg 的优秀教程以了解有关该主题的更多信息（关于谱聚类的教程, Statistics and Computing , 17(4): 395-416, 2007）。它可从 arXiv 免费获得，网址为http://arxiv.org/pdf/0711.0189v1.pdf。

请注意，在实践中，哪种聚类算法在给定数据集上表现最好并不总是很明显，特别是如果数据来自多个维度，难以或不可能可视化。此外，重要的是要强调成功的聚类不仅取决于算法及其超参数；相反，选择适当的距离度量和使用有助于指导实验设置的领域知识可能更为重要。

因此，在维度灾难的背景下，通常的做法是在执行聚类之前应用降维技术。这种无监督数据集的降维技术包括主成分分析和 t-SNE，我们在第 5 章“通过降维压缩数据”中介绍了这些技术。此外，将数据集压缩到二维子空间特别常见，这使我们能够使用二维散点图可视化集群和分配的标签，这对于评估结果特别有用。

概括

在本章中，您了解了三种不同的聚类算法，它们可以帮助我们发现数据中的隐藏结构或信息。我们从基于原型的方法 k-means 开始，它根据指定数量的聚类质心将示例聚类为球形。由于聚类是一种无监督的方法，我们不喜欢使用真实标签来评估模型的性能。因此，我们使用内在性能指标，例如肘部方法或轮廓分析，作为量化聚类质量的尝试。

然后，我们研究了一种不同的聚类方法：凝聚层次聚类。层次聚类不需要预先指定聚类的数量，结果可以以树状图表示形式可视化，这有助于解释结果。我们在本章中介绍的最后一个聚类算法是 DBSCAN，这是一种基于局部密度对点进行分组的算法，能够处理异常值和识别非球状形状。

在进入无监督学习领域之后，现在是时候介绍一些用于监督学习的最令人兴奋的机器学习算法了：多层人工神经网络。在最近的复兴之后，神经网络再次成为机器学习研究中最热门的话题。由于最近开发的深度学习算法，神经网络被认为是图像分类、自然语言处理和语音识别等许多复杂任务的最先进技术。在第 11 章，从零开始实现多层人工神经网络，我们将构建自己的多层神经网络。在第 12 章，使用 PyTorch 并行化神经网络训练，我们将使用 PyTorch 库，该库专门通过利用图形处理单元非常有效地训练具有多层的神经网络模型。