开放集域适应文献阅读五
Improved Open Set Doamin Adaptation With Backpropagation
- 1 问题与挑战
- 2 本文贡献
- 3 方法
- 4 小结
- 参考文献
1 问题与挑战
Saito 提出了一种由 t t t 参数化的二元交叉熵损失,它可以将未知目标样本与已知目标样本中分离。然而,如何理解二元交叉熵损失仍然是个谜。
2 本文贡献
- 作者利用 Kullback-Leiber(KL)距离提供了对二进制交叉熵损失的深刻理解;
- 并进一步提出了用对称的 Kullback-Leibler(KL)距离损失来代替二进制交叉熵损失改进的OSDA-BP方法。
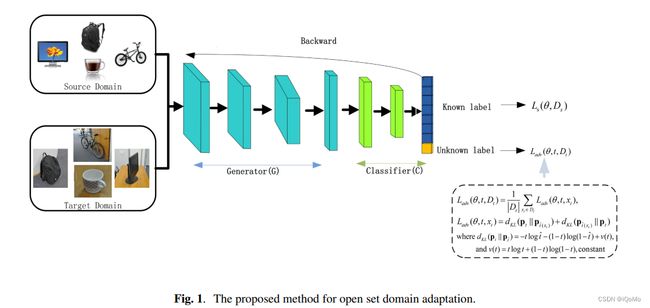
3 方法
因此, f ( θ , x ) f(\theta, x) f(θ,x) 输出任何输入图像 x x x 的 K + 1 K+1 K+1 维概率向量,其形式为:
f ( θ , x ) = { P ( cls ( x ) = 1 ) … P ( cls ( x ) = K + 1 ) } f(\theta, x)=\{P(\operatorname{cls}(x)=1) \ldots P(\operatorname{cls}(x)=K+1)\} f(θ,x)={P(cls(x)=1)…P(cls(x)=K+1)}
对于开放集域适应,第一个目标是将已知目标样本正确分类到相应的已知类中。为此,训练网络以最小化源域中 θ θ θ 上的标准交叉熵损失 L s L_s Ls:
L s ( θ , D s ) = 1 ∣ D s ∣ ∑ ( x s , y s ) ∈ D s l ( y s , f ( θ , x s ) ) L_s\left(\theta, D_s\right)=\frac{1}{\left|D_s\right|} \sum_{\left(x_s, y_s\right) \in D_s} l\left(y_s, f\left(\theta, x_s\right)\right) Ls(θ,Ds)=∣Ds∣1(xs,ys)∈Ds∑l(ys,f(θ,xs))
其中 l ( y , f ) = − ∑ j = 1 K y j log ( f j ) l(y, f)=-\sum_{j=1}^K y_j \log \left(f_j\right) l(y,f)=−∑j=1Kyjlog(fj), ∣ D s ∣ |Ds| ∣Ds∣ 表示集合 D s Ds Ds 的基数。 P ( c l s ( x ) = K + 1 ) = 0 P(cls(x)=K+1) = 0 P(cls(x)=K+1)=0,因为源域中没有任何未知样本。
第二个目标是训练分类器在未知和已知目标样本之间建立边界。对于这个目的,Saito 提出利用二元交叉熵损失:
L u ( θ , x t ) = − ( 1 − t ) ( 1 − log ( P ( cls ( x t ) = K + 1 ) ) ) − t log ( P ( cls ( x t ) = K + 1 ) ) \begin{aligned} L_u\left(\theta, x_t\right)=&-(1-t)\left(1-\log \left(P\left(\operatorname{cls}\left(x_t\right)=K+1\right)\right)\right) \\ &-t \log \left(P\left(\operatorname{cls}\left(x_t\right)=K+1\right)\right) \end{aligned} Lu(θ,xt)=−(1−t)(1−log(P(cls(xt)=K+1)))−tlog(P(cls(xt)=K+1))
以便分离任何未知样本 x t ∈ D t x_t \in D_t xt∈Dt 来自已知样本,其中 t t t 通常设置为0.5。
再次采用二元交叉熵损失的平均形式,即,
L u ( θ , D t ) = 1 ∣ D t ∣ ∑ x t ∈ D t L u ( θ , x t ) L_u\left(\theta, D_t\right)=\frac{1}{\left|D_t\right|} \sum_{x_t \in D_t} L_u\left(\theta, x_t\right) Lu(θ,Dt)=∣Dt∣1xt∈Dt∑Lu(θ,xt)
作者为这种二元交叉熵损失提供了一些见解。设 p t = ( t , 1 − t ) \mathbf{p}_t = (t,1− t) pt=(t,1−t) 表示由 0 < t < 1 0<t<1 0<t<1 参数化的二元分布。对于任何目标样本 x t x_t xt,设 t ^ ≜ P ( cls ( x t ) = K + 1 ) \hat{t} \triangleq P\left(\operatorname{cls}\left(x_t\right)=K+1\right) t^≜P(cls(xt)=K+1) 和 p t ^ = ( t ^ , 1 − t ^ ) \mathbf{p}_{\hat{t}}=(\hat{t}, 1-\hat{t}) pt^=(t^,1−t^),然后,作者将 p t \mathbf{p}_t pt 和 p t ^ \mathbf{p}_{\hat{t}} pt^ 之间的 Kullback-Leibler(KL)距离写成
d K L ( p t ∥ p t ^ ) = t log t t ^ + ( 1 − t ) log 1 − t 1 − t ^ = − t log t ^ − ( 1 − t ) log ( 1 − t ^ ) + ν ( t ) , \begin{aligned} d_{K L}\left(\mathbf{p}_t \| \mathbf{p}_{\hat{t}}\right) &=t \log \frac{t}{\hat{t}}+(1-t) \log \frac{1-t}{1-\hat{t}} \\ &=-t \log \hat{t}-(1-t) \log (1-\hat{t})+\nu(t), \end{aligned} dKL(pt∥pt^)=tlogt^t+(1−t)log1−t^1−t=−tlogt^−(1−t)log(1−t^)+ν(t),
其中 ν ( t ) = t log t + ( 1 − t ) log ( 1 − t ) \nu(t)=t \log t+(1-t) \log (1-t) ν(t)=tlogt+(1−t)log(1−t) 是固定 t t t 的常数。
现在 Saito 中提出的二元交叉熵损失可以被视为 ( t , 1 − t ) (t, 1−t) (t,1−t) 和 ( P ( c l s ( x t ) = K + 1 ) , 1 − P ( c l s ( x t ) = K + 1 ) ) (P(cls(x_t) = K + 1), 1−P(cls(x_t) = K + 1)) (P(cls(xt)=K+1),1−P(cls(xt)=K+1)) 之间的 K L距离,省略了 ν ( t ) ν(t) ν(t)。通过设置 t = 0.5 t = 0.5 t=0.5,为训练后的网络提供了一种合理的机制来区分已知类和未知类。
由于二元交叉熵损失本质上是一个KL距离,我们可以进一步采用它的对称形式为
L a d v ( θ , t , D t ) = 1 ∣ D t ∣ ∑ x t ∈ D t L a d v ( θ , t , x t ) L a d v ( θ , t , x t ) = d K L ( p t ∥ p t ^ ( x t ) ) + d K L ( p t ^ ( x t ) ) ∥ p t ) \begin{aligned} L_{a d v}\left(\theta, t, D_t\right) &=\frac{1}{\left|D_t\right|} \sum_{x_t \in D_t} L_{a d v}\left(\theta, t, x_t\right) \\ L_{a d v}\left(\theta, t, x_t\right) &\left.=d_{K L}\left(\mathbf{p}_t \| \mathbf{p}_{\hat{t}\left(x_t\right)}\right)+d_{K L}\left(\mathbf{p}_{\hat{t}\left(x_t\right)}\right) \| \mathbf{p}_t\right) \end{aligned} Ladv(θ,t,Dt)Ladv(θ,t,xt)=∣Dt∣1xt∈Dt∑Ladv(θ,t,xt)=dKL(pt∥pt^(xt))+dKL(pt^(xt))∥pt)
总损失:
L ( θ , t ) = L s ( θ , D s ) + λ 1 L a d v ( θ , t , D t ) L(\theta, t)=L_s\left(\theta, D_s\right)+\lambda_1 L_{a d v}\left(\theta, t, D_t\right) L(θ,t)=Ls(θ,Ds)+λ1Ladv(θ,t,Dt)
总体训练目标:
min θ c L s ( θ , D s ) + λ 1 L a d v ( θ , t , D t ) min θ q L s ( θ , D s ) − λ 1 L a d v ( θ , t , D t ) \begin{aligned} &\min _{\theta_c} L_s\left(\theta, D_s\right)+\lambda_1 L_{a d v}\left(\theta, t, D_t\right) \\ &\min _{\theta_q} L_s\left(\theta, D_s\right)-\lambda_1 L_{a d v}\left(\theta, t, D_t\right) \end{aligned} θcminLs(θ,Ds)+λ1Ladv(θ,t,Dt)θqminLs(θ,Ds)−λ1Ladv(θ,t,Dt)
4 小结
理解的很是牵强 ^ _ ^!
参考文献
[1] Fu J , Wu X , Zhang S , et al. Improved Open Set Domain Adaptation with Backpropagation[C]// 2019 IEEE International Conference on Image Processing (ICIP). IEEE, 2019.