PaddlePaddle入门实践——初识卷积神经网络

CNN基础介绍

卷积操作

  回想线性的神经网络关于输入输出$y=wx+b$的计算，我们通过链式求导法则获取权重$w$，而在CNN中，权重$w$将由卷积核来计算。

单通道卷积

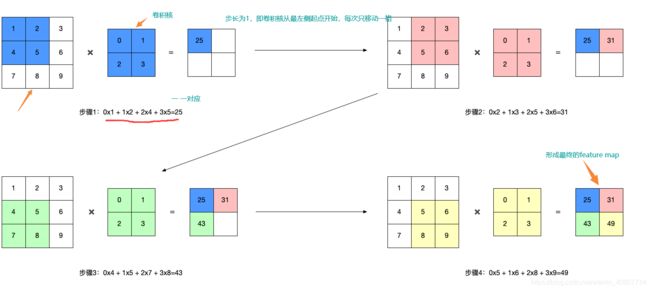
  在这里，输入图像被表示成单通道的3x3矩阵，像素点分布在矩阵上。卷积核中的值通过训练过程学到，卷积核在图像中，经过卷积计算和一定的横向步长以及纵向步长，移动到终点，此时得出一个新的2x2矩阵，即特征图。而特征图的$w$（宽）和$h$（高）的确定公式如下：
$$w=\frac{x_w+2P_w-f_w}{s_w}+1$$
$$h=\frac{x_h+2P_h-f_h}{s_h}+1$$
其中，$x_w$指输入图像的宽，$x_h$指输入图像的高；$f_w$指的是卷积核的宽，$f_h$指的是卷积核的高；$P_w$指横向Padding填充，$P_h$指纵向Padding填充；$s_w$指横向步长，$s_h$指纵向步长。

多通道卷积

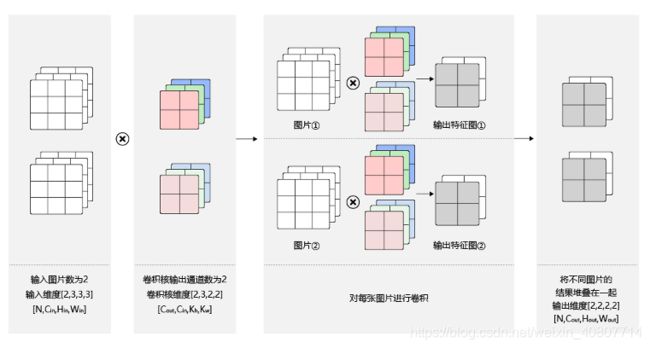
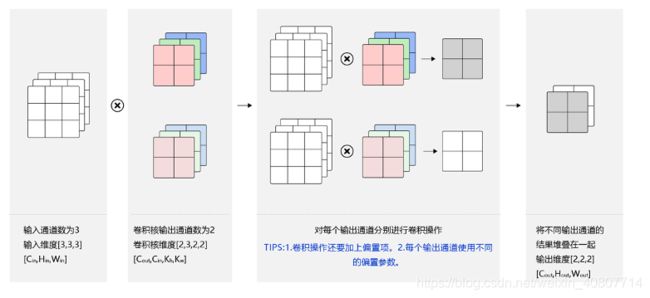
  由于很多图像是RGB格式，对应的就是三通道，因此我们常用多通道卷积。这里要注意一个误区，并不是输入图像通道多了，输出结果的通道就多了；也不是卷积核输入通道多了，输出结果的通道就多了。下图表示的是三通道的输入图像经过一个三通道的卷积核得到一个单通道的特征表示。当然，这个计算过程并不是唯一的，比如卷积核的个数所延伸出的多维度的滑动和神经元的加权求和中的“权”（下图直接将每个输入通道分别计算并求和），换句话说，可以玩出花来~

多通道输出

  输出通道的数目通常也被称作卷积核的个数。下图有两个卷积核，深色代表第一个卷积核的三个输入通道；浅色代表第二个卷积核的三个输入通道。

Batch

  卷积核信息不变，卷积操作会多一定的倍数（和样本数有关）。

池化层

  池化是使用某一位置的相邻输出的总体统计特征代替网络在该位置的输出，其好处是当输入数据做出少量平移时，经过池化函数后的大多数输出还能保持不变。比如：当识别一张图像是否是人脸时，我们需要知道人脸左边有一只眼睛，右边也有一只眼睛，而不需要知道眼睛的精确位置，这时候通过池化某一片区域的像素点来得到总体统计特征会显得很有用。由于池化之后特征图会变得更小，如果后面连接的是全连接层，能有效的减小神经元的个数，节省存储空间并提高计算效率。
  池化层是特征选择和信息过滤的过程，过程中会损失一部分信息，但是会同时会减少参数和计算量，在模型效果和计算性能之间寻找平衡，随着运算速度的不断提高，慢慢可能会有一些设计上的变化，现在有些网络已经开始少用或者不用池化层。

平均池化

  对邻域内特征点求平均。以下图为例，4x4原图像经过2x2的卷积池化，在对应卷积核大小的邻域内求平均值，池化的步长于卷积核的大小有关，相当于做特征采样。

• 正向传播：邻域内取平均
• 反向传播：特征值根据领域大小被平均，然后传给每个索引位置
  

最大池化

  顾名思义，对邻域内特征点取最大。能很好的保留一些关键的纹理特征，现在更多的再使用最大池化而很少用平均池化。

• 正向传播：邻域内取平均
• 反向传播：将特征值填充到正向传播中，值最大的索引位置，其他位置补0
  

padding

  padding的一个显著作用在于通过加宽或加高原有的输出图像，使得经过卷积操作之后的输出图像大小与原图像大小一致或是有其他的形变。这类似于我们学习几何过程中的添加辅助线技巧。
  还有一个好处，当我们使用原图像时，能很明显地发现在卷积操作中，越靠近中心的元素，被计算次数越多，而边缘元素会被忽略。为了能避免边缘信息的特征丢失，我们可以在原图像外围做填充0的操作，这样就增加了对边缘信息的特征提取。

激活函数

Sigmoid

Tanh

  观察图像发现，Sigmoid和Tanh的变化范围有限。Sigmoid和Tanh激活函数有共同的缺点：即在z很大或很小时，梯度几乎为零，因此使用梯度下降优化算法更新网络很慢。

ReLU

  Relu目前是选用比较多的激活函数，但是也存在一些缺点，在z小于0时，斜率即导数为0。为了解决这个问题，后来也提出来了Leaky Relu激活函数，不过目前使用的不是特别多。

Dropout

  当一个复杂的前馈神经网络被训练在小的数据集时，容易造成过拟合。为了防止过拟合，可以通过随机丢弃部分特征节点的方式来减少这个问题发生。

LeNet-5实践——手写数字识别

  在我上一篇写的总结（PaddlePaddle入门实践——手写数字识别）中，我们采用了单隐层、线性变换的全连接神经网络模型来实现功能，本次总结我们将继续着眼于手写数字识别，所不同的是，我们会使用CNN的经典结构LeNet-5来达成目的。
  Lenet是Yann LeCun等人在1998年提出的卷积神经网络结构，它的提出定义了CNN的基本结构：卷积层、池化层、全连接层。

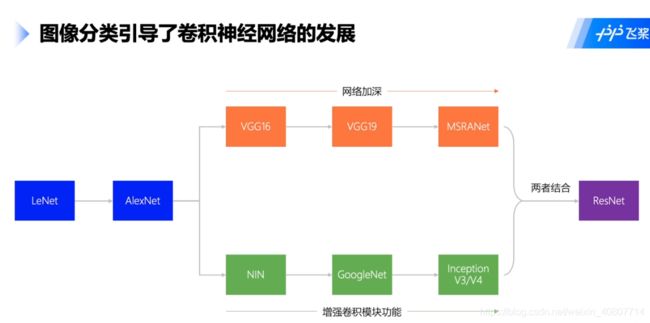
同时，图像分类任务也引导了CNN的发展，下图是CNN改进的部分策略。

数据准备

数据加载和预处理

import paddle
import numpy as np
import matplotlib.pyplot as plt

# 数据预处理
import paddle.vision.transforms as T

# 数据预处理
transform = T.Normalize(mean=[127.5], std=[127.5])

# 训练数据集
train_dataset = paddle.vision.datasets.MNIST(mode='train', transform=transform)

# 验证数据集
eval_dataset = paddle.vision.datasets.MNIST(mode='test', transform=transform)

print('训练样本量：{}，测试样本量：{}'.format(len(train_dataset), len(eval_dataset)))

查看数据

  MNIST数据格式(image,label)

print('图片：')
print(type(train_dataset[0][0]))
print(train_dataset[0][0])
print('标签：')
print(type(train_dataset[0][1]))
print(train_dataset[0][1])

# 可视化展示
plt.figure()
plt.imshow(train_dataset[0][0].reshape([28,28]), cmap=plt.cm.binary)
plt.show()

模型选择和组网

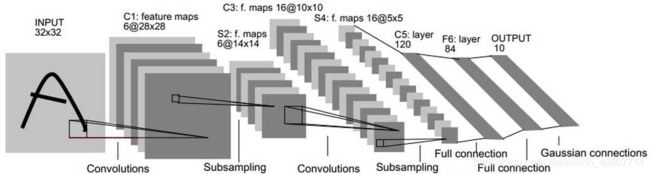
  选用LeNet-5网络结构，论文地址：https://ieeexplore.ieee.org/document/726791

每个阶段用到的Layer

原论文模型复现

import paddle.nn as nn

network = nn.Sequential(
    nn.Conv2D(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=0),  # C1 卷积层
    nn.Tanh(),
    nn.AvgPool2D(kernel_size=2, stride=2),  # S2 平局池化层
    nn.Sigmoid(),   # Sigmoid激活函数
    nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0),  # C3 卷积层
    nn.Tanh(),
    nn.AvgPool2D(kernel_size=2, stride=2),  # S4 平均池化层
    nn.Sigmoid(),  # Sigmoid激活函数
    nn.Conv2D(in_channels=16, out_channels=120, kernel_size=5, stride=1, padding=0), # C5 卷积层
    nn.Tanh(),
    nn.Flatten(),
    nn.Linear(in_features=120, out_features=84), # F6 全连接层
    nn.Tanh(),
    nn.Linear(in_features=84, out_features=10) # OUTPUT 全连接层
)

模型可视化

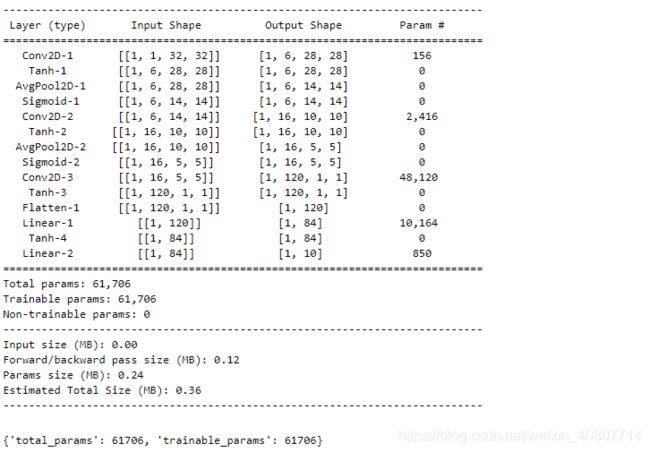
paddle.summary(network, (1, 1, 32, 32))

改进模型

Sequential写法

import paddle.nn as nn

network_2 = nn.Sequential(
    nn.Conv2D(in_channels=1, out_channels=6, kernel_size=3, stride=1, padding=1),
    nn.ReLU(),
    nn.MaxPool2D(kernel_size=2, stride=2),
    nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0),
    nn.ReLU(),
    nn.MaxPool2D(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(in_features=400, out_features=120),  # 400 = 5x5x16，输入形状为32x32， 输入形状为28x28时调整为256
    nn.Linear(in_features=120, out_features=84),
    nn.Linear(in_features=84, out_features=10)
)

模型可视化

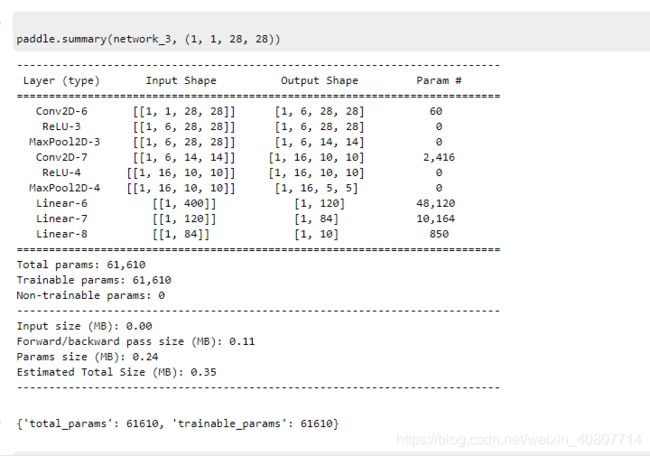
paddle.summary(network_2, (1, 1, 28, 28))

Sub Class写法

class LeNet(nn.Layer):
    """
    继承paddle.nn.Layer定义网络结构
    """

    def __init__(self, num_classes=10):
        """
        初始化函数
        """
        super(LeNet, self).__init__()

        self.features = nn.Sequential(
            nn.Conv2D(in_channels=1, out_channels=6, kernel_size=3, stride=1, padding=1),  # 第一层卷积
            nn.ReLU(), # 激活函数
            nn.MaxPool2D(kernel_size=2, stride=2),  # 最大池化，下采样
            nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0), # 第二层卷积
            nn.ReLU(), # 激活函数
            nn.MaxPool2D(kernel_size=2, stride=2) # 最大池化，下采样
        )

        self.fc = nn.Sequential(
            nn.Linear(400, 120),  # 全连接
            nn.Linear(120, 84),   # 全连接
            nn.Linear(84, num_classes) # 输出层
        )

    def forward(self, inputs):
        """
        前向计算
        """
        y = self.features(inputs)
        y = paddle.flatten(y, 1)
        out = self.fc(y)

        return out

network_3 = LeNet()

模型可视化

paddle.summary(network_2, (1, 1, 28, 28))

PaddlePaddle高层API写法

network_4 = paddle.vision.models.LeNet(num_classes=10)

模型可视化

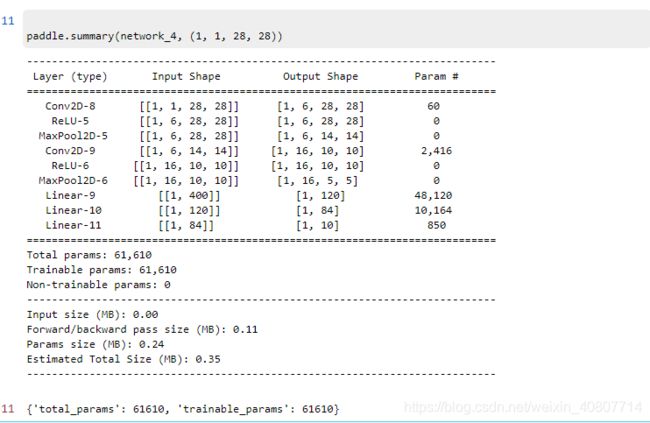
paddle.summary(network_2, (1, 1, 28, 28))

模型训练和调优

# 模型封装
model = paddle.Model(network_2)

# 模型配置
model.prepare(paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters()), # 优化器
              paddle.nn.CrossEntropyLoss(), # 损失函数
              paddle.metric.Accuracy()) # 评估指标

# 启动全流程训练
model.fit(train_dataset,  # 训练数据集
          eval_dataset,   # 评估数据集
          epochs=5,       # 训练轮次
          batch_size=64,  # 单次计算数据样本量
          verbose=1)      # 日志展示形式

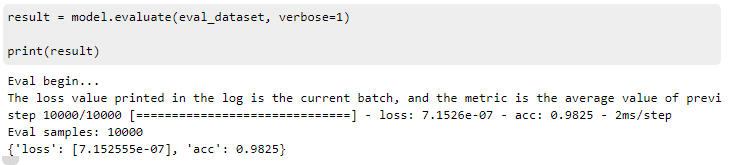
模型评估

result = model.evaluate(eval_dataset, verbose=1)

print(result)

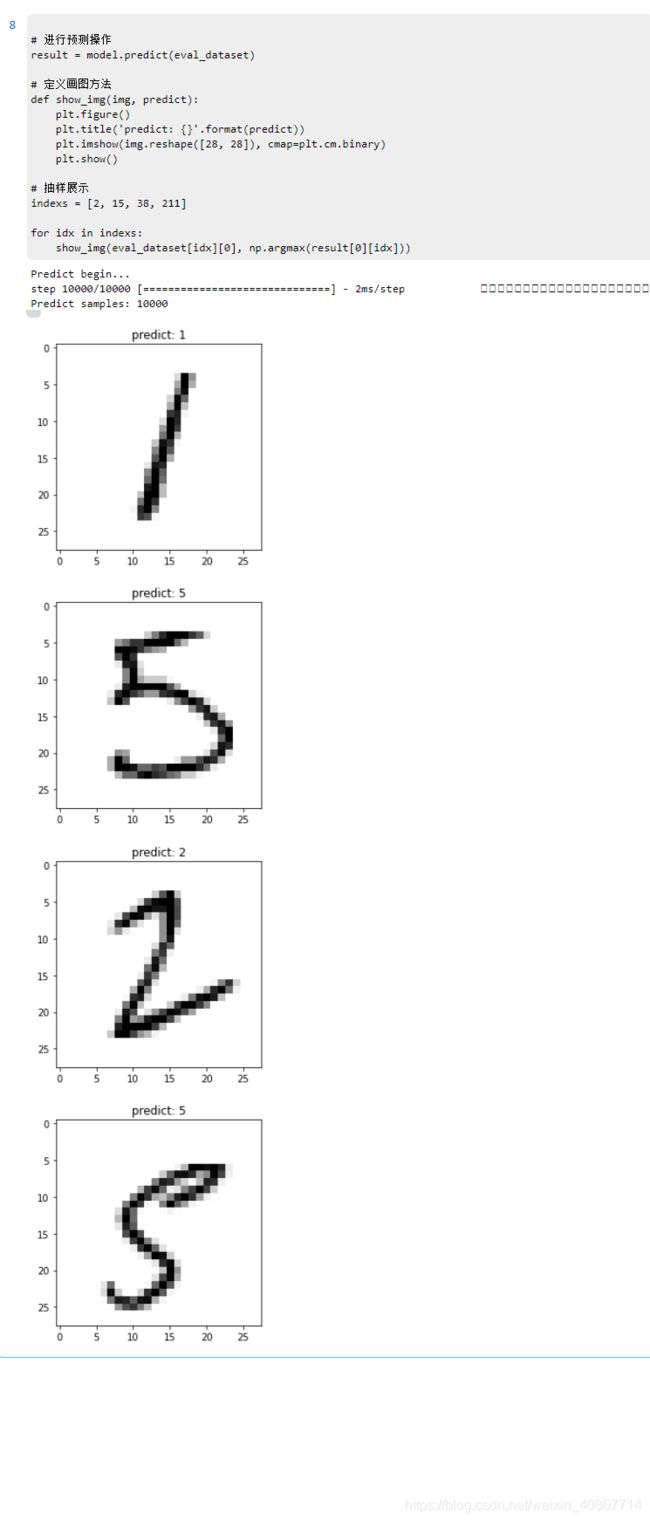
批量预测

# 进行预测操作
result = model.predict(eval_dataset)

# 定义画图方法
def show_img(img, predict):
    plt.figure()
    plt.title('predict: {}'.format(predict))
    plt.imshow(img.reshape([28, 28]), cmap=plt.cm.binary)
    plt.show()

# 抽样展示
indexs = [2, 15, 38, 211]

for idx in indexs:
    show_img(eval_dataset[idx][0], np.argmax(result[0][idx]))

参考

• paddle深度学习第2课案例1基础知识
• paddle深度学习第2课案例1初识卷积神经网络