图机器学习——4.3 节点分类:Correct & Smooth (C&S)
Correct & Smooth (C&S)
1)方法介绍
如今,图神经网络(GNN)是图学习方面的主要技术,在很多图结构相关的预测任务上取得了最顶尖的成绩,但在节点分类任务上,Correct & Smooth (C&S)可谓异军突起,通过基础浅层模型和“矫正”与“光滑”两个基于标签传播的后处理步骤即可达到甚至超越当前主流 GNNs 模型的性能,并且参数量和训练及运行时间远低于复杂的 GNNs 结构。
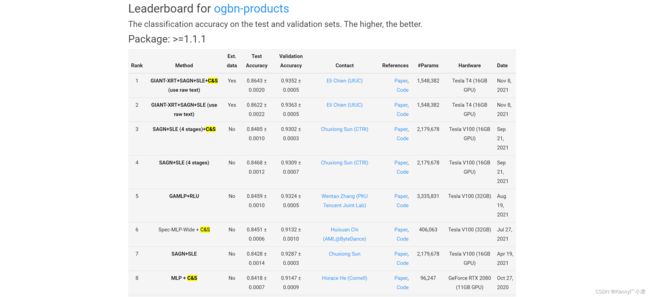
下图为截至当前(2021/11/21)最顶尖的图中的节点分类方法排名,数据来源(Leaderboards for Node Property Prediction)
可以发现同一种基础结构中,表现最好的都是添加了C&S方法的模型。
C&S方法分为三步:
- 训练基础训练器(base predictor);
- 使用基础预测变量预测所有节点的软标签(soft labels,其实就是类别的概率);
- 对使用图结构预测的结果进行后处理,而后得到最终预测结果。
后处理步骤(Correct & Smooth)包括两步:
- 误差矫正 (Correct step):利用训练数据中的残差来纠正测试数据中的误差;
- 平滑标签 (Smooth step):平滑测试数据中的预测结果。
2)案例说明
下面以一个实际的例子对整个过程进行解释说明。
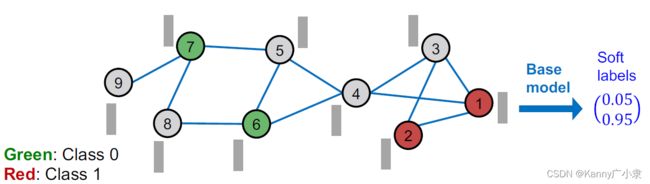
a. 训练基础分类器
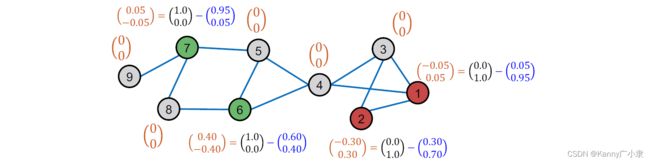
如上图所示,基础图结构是有部分节点标签已知,部分标签未知,但所有节点都有特征信息。首先需要利用特征信息进行分类模型的构建。这个模型可以为logistic model,神经网络模型等。由此可计算出每个节点的两个类别的概率,称为软标签。上图节点1的软标签为 ( 0.05 , 0.95 ) ⊤ (0.05, 0.95)^\top (0.05,0.95)⊤,其中0.05为第0类的概率;0.95为第1类的概率。
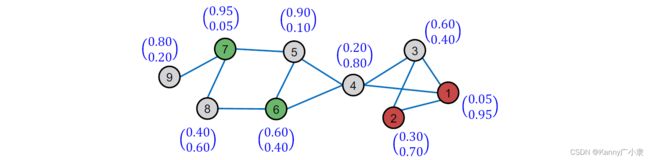
b. 训练所有节点的软标签
基于上一步构建的模型,我们可以得到所有节点训练的软标签。
c. C&S 两步后处理过程
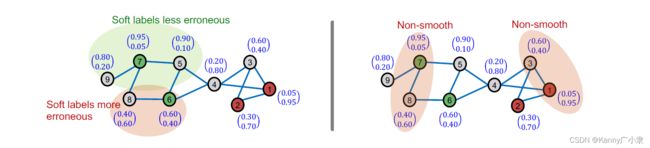
此时我们得到的预测结果并没有利用到图的信息。回忆图的基本性质为同质性,也就是边相连的两个节点预测的误差应该是相似或者说正相关的;同样,标签也应该具有类似的特性。下面我们利用图的这种信息传递性来平滑节点的预测误差与标签。
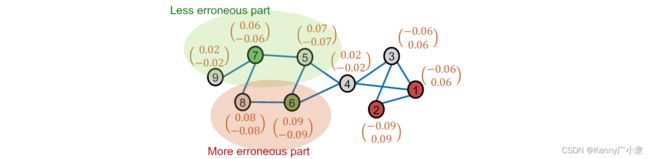
误差矫正目的是让某些节点误差比较大的节点(预测概率倾向于0.5)更加精准地进行预测(下左图);平滑标签的目的是让相邻两个节点之间的预测概率尽可能不要有太大的差异(下右图)。
① 误差矫正
首先初始化网络,计算每个节点的训练误差(残差)。没有标签的节点初始误差记为 0 0 0,则计算出来的误差如下图所示:
初始误差为:
E ( 0 ) = ( − 0.05 0.05 − 0.30 0.30 0 0 0 0 0 0 0.40 − 0.40 0.05 − 0.05 0 0 0 0 ) \boldsymbol{E}^{(0)}=\left(\begin{array}{cc} -0.05 & 0.05 \\ -0.30 & 0.30 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0.40 & -0.40 \\ 0.05 & -0.05 \\ 0 & 0 \\ 0 & 0 \end{array}\right) E(0)=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛−0.05−0.300000.400.05000.050.30000−0.40−0.0500⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞
此时我们需要按照图的结构,构建误差传播网络,迭代公式定义如下:
E ( t + 1 ) ← ( 1 − α ) ⋅ E ( t ) + α ⋅ A ~ E ( t ) \boldsymbol{E}^{(t+1)} \leftarrow(1-\alpha) \cdot \boldsymbol{E}^{(t)}+\alpha \cdot \widetilde{\boldsymbol{A}} \boldsymbol{E}^{(t)} E(t+1)←(1−α)⋅E(t)+α⋅A E(t)
其中, α \alpha α为超参数,控制保留多少比例上一步的信息(类似之前PageRank中的超参数),通过标准化的邻接矩阵 A ~ \widetilde{\boldsymbol{A}} A 传递多少信息。信息在此时为误差。标准化的邻接矩阵定义如下:
A ~ ≡ D − 1 / 2 ( I + A ) D − 1 / 2 \widetilde{\boldsymbol{A}} \equiv \boldsymbol{D}^{-1 / 2} (\boldsymbol{I} + \boldsymbol{A}) \boldsymbol{D}^{-1 / 2} A ≡D−1/2(I+A)D−1/2
其中, D ≡ diag ( d 1 , … , d N ) \boldsymbol{D} \equiv \operatorname{diag}\left(d_{1}, \ldots, d_{N}\right) D≡diag(d1,…,dN)为度矩阵(degree matrix)。利用上述形式的标准化邻接矩阵,而不直接使用邻接矩阵 A \boldsymbol{A} A是出于两方面的原因:
- 添加自连接(self-loop,加上单位阵 I \boldsymbol{I} I),是考虑了节点本身信息自传递的情况;
- 利用度矩阵进行标准化是考虑了邻居节点多的节点倾向于有更大的影响力的问题,从而不让度大的邻居节点对本节点的影响过大。
这也非常像基于频谱的 GCN(图卷积网络)利用标准化后的拉普拉斯算子的传递公式,其实含义是比较类似的,而且实际的效果会比较出众。
其次,针对标准化的邻接矩阵 A ~ \widetilde{\boldsymbol{A}} A 可以计算得到, λ = 1 \lambda = 1 λ=1为其最大特征值,对应的特征向量为 D 1 / 2 1 \boldsymbol{D}^{1 / 2} \mathbf{1} D1/21, 1 \mathbf{1} 1为全 1 1 1列向量(且所有特征值均在 [ − 1 , 1 ] [-1,1] [−1,1]区间),证明如下:
A ~ D − 1 / 2 1 = D − 1 / 2 A D − 1 / 2 D 1 / 2 1 = D − 1 / 2 A 1 = D − 1 / 2 ( A 1 ) = D − 1 / 2 ( D 1 ) = 1 ⋅ D 1 / 2 1 \widetilde{\boldsymbol{A}} \boldsymbol{D}^{-1 / 2} \mathbf{1}=\boldsymbol{D}^{-1 / 2} \boldsymbol{A} \boldsymbol{D}^{-1 / 2} \boldsymbol{D}^{1 / 2} \mathbf{1}=\boldsymbol{D}^{-1 / 2} \boldsymbol{A} \mathbf{1}=\boldsymbol{D}^{-1 / 2} (\boldsymbol{A} \mathbf{1})=\boldsymbol{D}^{-1 / 2} (\boldsymbol{D} \mathbf{1})=1 \cdot \boldsymbol{D}^{1 / 2} \mathbf{1} A D−1/21=D−1/2AD−1/2D1/21=D−1/2A1=D−1/2(A1)=D−1/2(D1)=1⋅D1/21
此外, A ~ \widetilde{\boldsymbol{A}} A 可以当做信息传递的转移矩阵,其任意 K K K次冥( A ~ K \widetilde{\boldsymbol{A}}^{K} A K)的特征值均在 [ − 1 , 1 ] [-1,1] [−1,1]之中,且最大特征值为 1 1 1。因此这种信息传递会比较稳定。
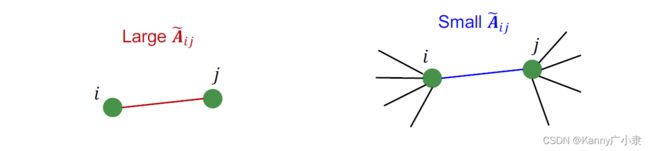
直观上来理解 A ~ \widetilde{\boldsymbol{A}} A ,我们取其中一个元素 A ~ i j = 1 d i d j \widetilde{\boldsymbol{A}}_{i j} = \frac{1}{\sqrt{d_{i}} \sqrt{d_{j}}} A ij=didj1,其为 i , j i,j i,j节点之间传递信息的权重。
- 若节点 i i i 和 j j j 仅相互连接,没有其他节点连接到 i i i 和 j j j,那么此时传递的权重非常大;
- 若节点 i i i 和 j j j 除了两者之间的连接外,还与许多其他节点连接,那么传递的权重会比较小。
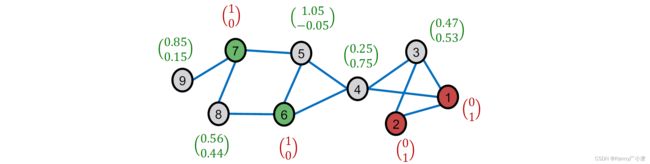
我们将 α \alpha α设定为 0.8 0.8 0.8,在三轮迭代传播后,每个节点的误差如下:
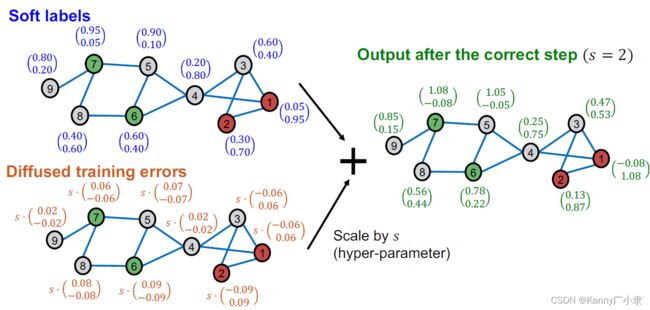
而后在预测的软标签中加入经过缩放尺度 s s s缩放的扩散后的训练误差,得到我们第二步误差矫正的结果。
② 平滑标签
在平滑标签这一步骤中,我们的目的是通过图结构,传递已标注节点正确的软标签(假设邻居节点倾向于相同的标签)。此时我们的初始标签如下:
如上图,需要注意的是,对于有标签的节点,我们用真实标签替代上一步估计出来的,然后将正确的标签像附近相邻节点传递信息。初始的标签矩阵如下:
Z ( 0 ) = ( 0 1 0 1 0.47 0.53 0.25 0.75 1.05 − 0.05 1 0 1 0 0.56 0.44 0.85 0.15 ) \boldsymbol{Z}^{(0)}=\left(\begin{array}{cc} 0 & 1 \\ 0 & 1 \\ 0.47 & 0.53 \\ 0.25 & 0.75 \\ 1.05 & -0.05 \\ 1 & 0 \\ 1 & 0 \\ 0.56 & 0.44 \\ 0.85 & 0.15 \end{array}\right) Z(0)=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛000.470.251.05110.560.85110.530.75−0.05000.440.15⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞
迭代公式类似上一步的误差矫正,定义如下:
Z ( t + 1 ) ← ( 1 − α ) ⋅ Z ( t ) + α ⋅ A ~ Z ( t ) \boldsymbol{Z}^{(t+1)} \leftarrow(1-\alpha) \cdot \boldsymbol{Z}^{(t)}+\alpha \cdot \widetilde{A} \boldsymbol{Z}^{(t)} Z(t+1)←(1−α)⋅Z(t)+α⋅A Z(t)
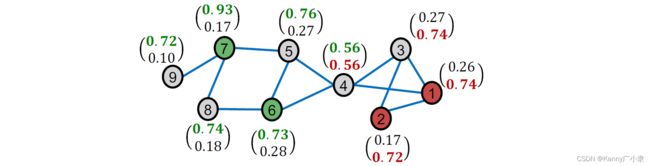
迭代三次之后的结果如下所示:
最后,由于节点两个值加起来不为 1 1 1,因此我们选择较大的值为最终的类别。
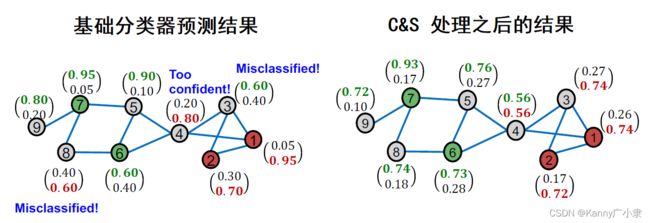
我们再来比较一下经过基础分类器得到的结果,以及经过C&S之后的结果,可以发现结果提升了非常多。
参考
- CS224W: Machine Learning with Graphs