MATLAB-直方图均衡化
博客首页：安静到无声
⛳️ 欢迎关注 ❤️ 点赞 收藏 ✏️ 留言
系列专栏：Verilog学习
由于HDLBits刷题并不方便，在这里给大家强烈推荐一款嵌入式硬件模拟面试、刷题神器——牛客网（ [ Verilog，C等基础，更有一些硬件知识点拨 ）
❤️ 点击免费注册和我一起刷题吧
1. 直方图
定义（1）：一个灰度级在范围 [ 0 , L − 1 ] [0,L-1] [0,L−1]的数字图像的直方图是一个离散函数:
h ( r k ) = n k h\left(r_{k}\right)=n_{k} h(rk)=nk其中 n k n_k nk是图形中灰度级为 r k r_k rk的像素个数， r k r_k rk是第 k k k个灰度级， k = 0 , 1 , 2 , … , L − 1 k=0,1,2, \ldots, L-1 k=0,1,2,…,L−1，由于 r k r_k rk的增量是1，直方图可表示为：
p ( k ) = n k p(k)=n_{k} p(k)=nk将图像中不同灰度级像素出现的次数。
定义（2）:
一个灰度级在范围 [ 0 , L − 1 ] [0,L-1] [0,L−1]的数字图像的直方图是一个离散函数：
p ( r k ) = n k / n p\left(r_{k}\right)=n_{k} / n p(rk)=nk/n其中 n n n是图像总的像素个数， n k n_k nk是图形中灰度级为 r k r_k rk的像素个数， r k r_k rk是第 k k k个灰度级， k = 0 , 1 , 2 , … , L − 1 k=0,1,2, \ldots, L-1 k=0,1,2,…,L−1。
对比定义1和定义2，我们可以得到：
- 是函数值正则化到 [ 0 , 1 ] [0,1] [0,1]区间，成为实数函数。
- 函数值的范围与像素的总数无关。
- 给出灰度级 r k r_k rk在图像中出现的概率密度统计。
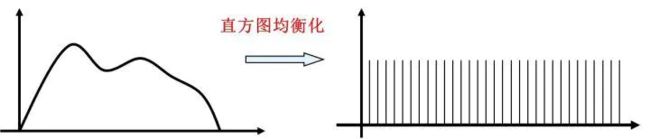
2. 直方图均衡化
直方图均衡化(Histogram Equalization) 又称直方图平坦化,实质上是对图像进行非线性拉伸,重新分配图像象元值,使一定灰度范围内象元值的数量大致相等。这样,原来直方图中间的峰顶部分对比度得到增强,而两侧的谷底部分对比度降低,输出图像的直方图是一个较平的分段直方图:如果输出数据分段值较小的话,会产生粗略分类的视觉效果。
直方图均衡化的作用是图像增强。
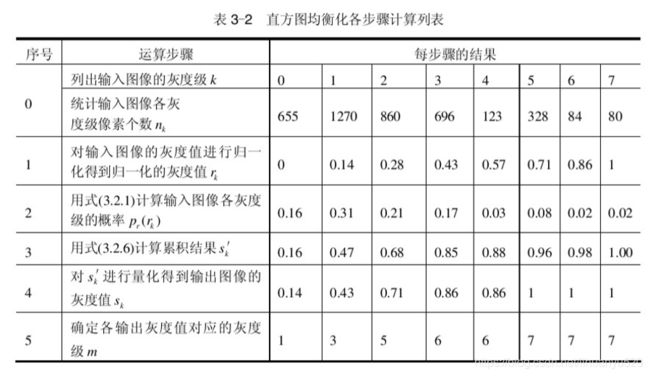
3. 实例
4. Matlab程序实现
要求：输入一幅灰度图像。
- 按比例降低整幅图像灰度；
- 对降低灰度后的图像进行直方图均衡化处理；
- 在同一个窗口输出显示原始图像和２种结果图像。
clc;clear all;
img = imread('G:\Python\04.Deep learning\07数字图像处理\01matlab作业\image\lena256.bmp');
subplot(131)
imshow(img),title("原图像");
%降低1/2的比例降低图像的灰度
img = img/2
subplot(132)
imshow(img),title("降低灰度后的图像");
[ROW,COL] = size(img);
% 统计每个像素值出现次数
count = zeros(1, 256);
for i = 1 : ROW
for j = 1 : COL
count(1, img(i, j) + 1) = count(1, img(i, j) + 1) + 1;
end
end
%统计每个像素出现的概率
T = zeros(1,256);
T = double(T);
count = double(count);
for i = 1 : 256
T(1,i) = count(1,i)/(ROW*COL)
end
%求累积概率
for i = 2 : 256
T(1,i) = T(1,i-1) + T(1,i);
end
img = double(img)
for i = 1 : ROW
for j = 1 : COL
img(i,j) = T(1, img(i, j) + 1) * 255;
end
end
img = uint8(img);
subplot(133)
imshow(img),title("均衡化后图像");
参考：数字图像处理，曹茂永编