(一)基于结构张量的分数阶变分光流模型——2021
基于结构张量的分数阶变分光流模型
- 1. Introduction
- 2. Related Work
- 3. HS Optical Flow Model
- 4. Local Structure Constraint Equation
-
- 4.1. Image Structure Tensor
- 4.2. Local Structure Constancy Constrain
- 5. Fractional Smoothness Constraint Equation
- 6. Improved Fractional Optical Flow Model
1. Introduction
图像序列或视频中的运动检测是各种图像处理项目的基本任务之一,在三维重建、运动物体分割、运动物体跟踪、视频压缩、自动驱动等领域的研究和工程实践中得到了广泛的应用。变分光流法是最常用的运动检测方法之一。HS光流模型[1]是最经典的变分光流模型。它由一个亮度恒定约束和一个全局平滑约束组成。亮度恒定约束要求像素的强度在运动过程中保持不变,而平滑约束假设图像中所有像素的运动速度都发生平滑变化。然而,这两个约束条件都是基于理想的假设。在实际应用中,这两个约束条件经常被违反。场景中的光照变化将打破亮度常数约束和全局平滑度约束,导致不同运动区域之间的边缘模糊。
为了提高变分光流模型的性能,还提出了其他几种对数据项的约束条件,如梯度常量约束[2]、拉普拉斯恒定约束[3]和 Hessian恒定约束[4],但这些约束条件在很大程度上取决于强度差。采用照明不变性描述符,如基于二元序列的[5]、基于实值的[6,7]和基于邻域的[8,9]来替代亮度恒定约束,但是这些描述符不能识别不同运动区域之间的边缘。结构张量[10–12],可以体现运动物体的形状特征,是一种不随环境因素而变化的局部结构特征。基于结构张量特征建立的局部结构光流模型(LSOFM)[13–15]可以提高其在光照变化场景中的鲁棒性。但是,当一个结构包含不同的运动部分时,LSOFM就会失效。
由于分数光流矢量梯度可以将局部邻域光流向量的特性融合到目标像素的光流向量中,增强了相同运动速度区域的完整性,从而保持不同运动区域之间光流场的不连续性。分数阶变分光流模型(FOVOFM)由Chen等人[16]提出,该模型在HS模型的光滑性项中使用了分数阶光滑性约束。e双分数阶变分光流模型(dfovofm)由Zhu等人[17]提出,并将分数阶导数应用于HS模型的数据项和平滑项。在[18]中提出了分数阶TV-L1光流模型。)e基于分数阶的光流模型忽略了图像中的结构信息,导致边缘和一些微小的运动区域存在误差。
本文提出了一种改进的变分光流模型。我们的模型由LSCC和FSC组成。LSCC不仅可以保证模型在光照变化场景中的鲁棒性,而且还可以增强图像中的轮廓。FSC不仅保留了不同运动区域之间的运动不连续,而且削弱了光照变化对光流估计的影响。本文提出的E模型结合了这两种约束条件的优点,解决了光流估计中的光照变化问题和运动不连续问题,可以识别出一个结构中的不同运动部分。
本文的贡献如下:
(1)设计了一种结合局部结构张量和分数阶偏差的新型光流模型,以提高照明变化的鲁棒性。
(2)提出了一种适用的模型简化方法
2. Related Work
在[19]中提出了一种基于全四维成本体积的光流模型,该模型应用了结构特征和立体匹配管道,获得了较高的精度。为了解决光流估计中由无纹理区域、运动边界和遮挡引起的问题,事后信任测量[20]用于评估流的每像素可靠性。闭塞仍然是关键的挑战之一。在[21]中,提出了一种对称光流模型来解决光流估计中的遮挡问题。在[22]中,提出了一种插值对应的方法来估计光流,但这些方法通常容易受到非刚性运动和大位移的影响;为了解决这个问题,在[23]中提出了稀疏对应的鲁棒插值。
[24]提出了一种结合有效的随机搜索策略的高效密集对应方案来估计的光流。[25]将具有稀疏种子到稀疏匹配的粗糙到精细的补丁匹配应用于光流估计,[26]提出了一种新的可微邻居搜索上采样(NSU)模块,以改进从粗到细的技术,以避免边缘、细条和孔中的光流误差。[27]采用一种利用全变分小波正则化的频域光流方法,利用频域正则化进行精确的光流估计。
随着人工智能的快速发展,基于深度学习的方法已被广泛应用于光流估计中。FlowNet[28]证明了cnn可以用来估计光流。在[29]中,设计了三个主要的改进:基于小位移的子网,采用堆叠架构对中间光流对第二幅图像进行扭曲,以及训练数据的时间表。设计了一种新的深度网络结构,即循环全对场变换来估计[30]中的光流。在[31]中提出了一种单高分辨率估计多尺度光流的可变形代价体积神经网络。PWC-Net[32]由金字塔处理、翘曲和成本组成,用于估计光流。网络利用当前的光流估计来扭曲第二幅图像的CNN特征,然后利用第一幅图像的扭曲特征和特征来构造一个代价体积。基于深度学习的方法的缺点是需要大量的真值,并且需要针对不同的应用对模型进行再训练。
3. HS Optical Flow Model
HS模型可以写成如下:
E ( u ) = E d a t a ( u ) + λ E s m o o t h ( u ) (1) E(u)=E_{data}(u)+\lambda E_{smooth}(u) \tag{1} E(u)=Edata(u)+λEsmooth(u)(1)其中 u = ( u , v ) u=(u,v) u=(u,v)表示光流向量,u为x轴上的光流值,v为y轴上的光流值,Edata(u)表示亮度约束方程,Esmooth(u)表示平滑约束方程,λ为平滑参数,其值由图像质量决定。在许多噪声干扰的模糊图像中,λ的值应该很大,反之亦然。
基于亮度恒定约束的亮度约束方程,假设一个像素的亮度值在运动过程中是恒定的,如下:
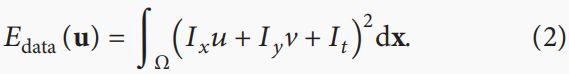
基于全局平滑约束的平滑约束方程,假设所有像素的运动速度变化平稳,即速度的导数很小,如下:
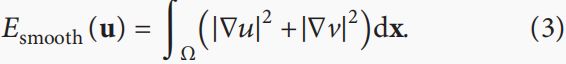
4. Local Structure Constraint Equation
图像局部几何特征组成的结构张量是光照变化、图像旋转、图像平移和图像缩放的不变特征。为了提高光流模型的鲁棒性,我们使用局部结构常数约束来代替亮度常数约束。
4.1. Image Structure Tensor
二维图像的局部结构张量可以表示为:
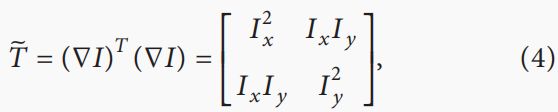
其中I表示亮度函数, ∇ = ( ∂ x , ∂ y ) ∇=(\partial x,\partial y) ∇=(∂x,∂y)是沿x轴和y轴的切向量, T ~ \tilde T T~是一个像素的结构张量。但 T ~ \tilde T T~很容易受到噪声的影响,所以它总是被高斯滤波器 G σ G_σ Gσ增强:
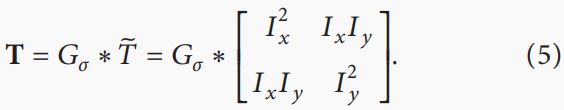
4.2. Local Structure Constancy Constrain
本文提出了局部结构恒常性约束(LSCC),以增强光流模型的鲁棒性。LSCC是基于图像中的局部结构在运动过程中不会发生变化的假设:
T ( x , y , t ) = T ( x + u , y + v , t + 1 ) (6) T(x,y,t)=T(x+u,y+v,t+1) \tag{6} T(x,y,t)=T(x+u,y+v,t+1)(6)
其中T(x,y,t)表示从一个像素(x,y)在 t t t帧的结构张量函数。然后,像素将从(x,y,t)移动到(x+u,y+v,t+1),(u,v)为光流值,T(x+u,y+v,t+1)表示t+1帧的结构张量。方程(6)表示结构张量在运动过程中不会发生变化。
利用泰勒级数展开式和忽略最小项,我们可以得到
T x u + T y v + T t = 0 (7) T_xu+T_yv+T_t=0 \tag{7} Txu+Tyv+Tt=0(7)
其中Tx,Ty和Tt是结构张量函数在x,y和t轴上的导数, T = [ a b c d ] , a = 1 / l ∑ x ∈ Ω ( x 0 ) w I x 2 , b = 1 / l ∑ x ∈ Ω ( x 0 ) w I x I y , c = 1 / l ∑ x ∈ Ω ( x 0 ) w I y 2 T=\left[\begin{matrix}a & b\\c & d\end{matrix}\right],a=1/l\sum_{x\in\Omega(x_0)}wI_x^2,b=1/l\sum_{x\in\Omega(x_0)}wI_xI_y,c=1/l\sum_{x\in\Omega(x_0)}wI_y^2 T=[acbd],a=1/l∑x∈Ω(x0)wIx2,b=1/l∑x∈Ω(x0)wIxIy,c=1/l∑x∈Ω(x0)wIy2,Ω(x0)表示目标点的局部邻域,l为归一化常数,w表示权重函数。
Edata(u)可以重写如下:
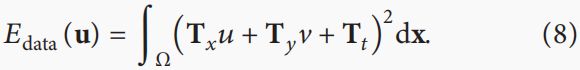
5. Fractional Smoothness Constraint Equation
在我们的模型中应用分数平滑约束(FSC),进一步提高光流估计的性能。在HS光流模型中,用分数阶导数代替光滑约束方程中的分数阶导数代替整数阶导数:

α是实数, α ∈ ( 1 , 2 ) \alpha\in(1,2) α∈(1,2),Esmooth(u)可设计如下:

6. Improved Fractional Optical Flow Model
结合LSCC和FSC,我们构建了改进后的光流模型;利用HS模型的结构,我们的光流模型可以描述如下:
![]()
利用欧拉-拉格朗日方程来最小化能量函数(11),在[14,15]中也可以看到类似的过程;然后,我们可以得到
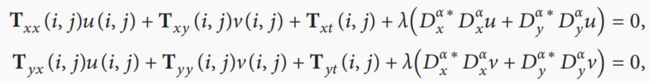
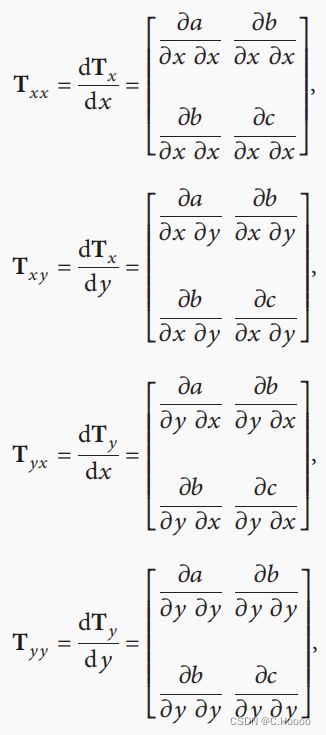
其中, D x α ∗ D x α u , D y α ∗ D y α u , D x α ∗ D x α v , D y α ∗ D y α v D^{α∗}_xD^α_xu,D^{α∗}_yD^α_yu,D^{α∗}_xD^α_xv,D^{α∗}_yD^α_yv Dxα∗Dxαu,Dyα∗Dyαu,Dxα∗Dxαv,Dyα∗Dyαv分别表示x轴和y轴上光流值u和v的对偶分数阶导数:
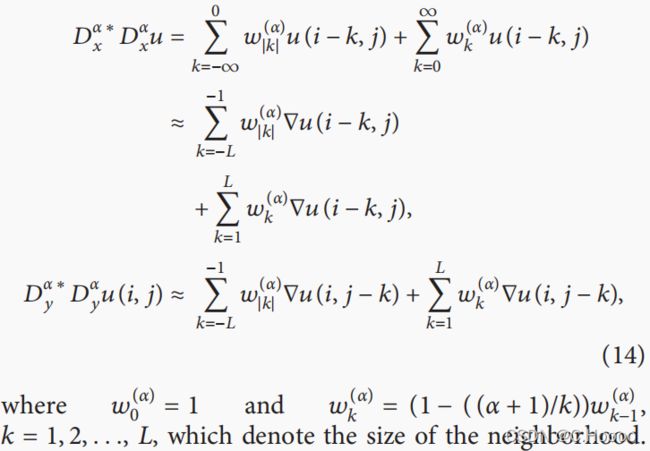
然后,我们可以得到

χ ( i , j ) χ(i,j) χ(i,j)表示的点(i,j)的一个邻域, k i j ˉ k_{\bar{ij}} kijˉ等于 max ( ∣ i ˉ − i ∣ , ∣ j ˉ − j ∣ ) \max(|\bar i−i|,|\bar j−j|) max(∣iˉ−i∣,∣jˉ−j∣), u ( i ˉ , j ˉ ) u(\bar i,\bar j) u(iˉ,jˉ)和 v ( i ˉ , j ˉ ) v(\bar i,\bar j) v(iˉ,jˉ)是光流向量的平均值,u(i,j)和v(i,j)是邻域内每个像素的x轴和y轴上的光流向量的坐标。
根据以上,光流估计公式如下:
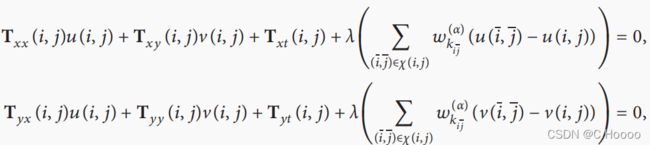
其中,λ为平滑度参数,根据Huerst和Xie[33].所述。参数λ的值由图像质量决定;当图像为暗、不明、模糊或有噪声时,λ应较大。否则,λ应该很小。在我们的算法中,我们在相对清晰的图像中选择λ∈[5.0,10.0],在相对模糊的图像中选择λ∈[10.0,15.0], α \alpha α是光滑项中分数阶的阶数,根据Chen[15],α=1.3或1.4。α=1.3的准确率相对高于α=1.4,而后者需要的迭代次数更少。
利用高斯-塞德尔方法,可以通过重复迭代可以得到精确的光流值。当精度达到要求(相邻两次迭代之间的光流值之差小于阈值)时,迭代将停止。