复现《Deep Leakage from Gradients》的攻击实验

复现《Deep Leakage from Gradients》的攻击实验

Deep Leakage from Gradients

在GitHub上找到一个在pytorch实现《Deep Leakage from Gradients》论文中对CIFAR100数据集攻击的实验，加上了自己的理解

class LeNet(nn.Module):
def __init__(self):
    super(LeNet, self).__init__()
    act = nn.Sigmoid
    self.body = nn.Sequential(
        nn.Conv2d(3, 32, kernel_size=5, padding=5//2, stride=2),
        act(),
        nn.Conv2d(32, 32, kernel_size=5, padding=5//2, stride=2),
        act(),
        nn.Conv2d(32, 64, kernel_size=5, padding=5//2, stride=1),
        act(),
    )
    self.fc = nn.Sequential(
        nn.Linear(4096, 100)
    )
    
def forward(self, x):
    out = self.body(x)
    out = out.view(out.size(0), -1)
    #print(out.size())
    out = self.fc(out)
    return out

`

原代码有两种模型，一种Lenet，一种为Resnet,我用的第一种其中它源代码的卷积通道都为12，但是自己在实现的时候发现最后恢复不了原始的图片，全部都是噪音，不知到它是怎么实现的，摊手.jpg。然后自己将通道数换成32，32，64，然后就奇迹发生了，只迭代了0次loss就0.001？？？,可能是自己实现的有问题吧。
上图！

有没有很奇怪的感觉？？ ，但是可以恢复出原始数据，(^_)，管不了这么多了
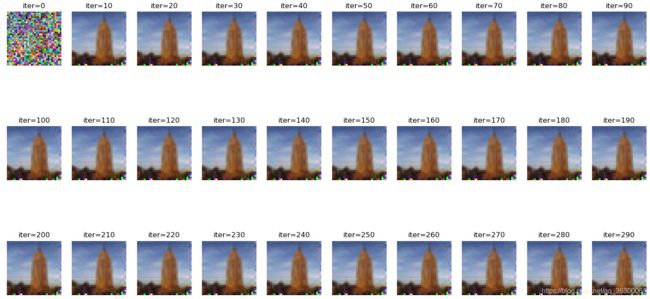异常清晰啊，朋友们，不得不说这篇论文的idel是真的棒啊！！！
最后上主要代码：
修改了一些变量名并且加入了一些注释方便理解

# -*- coding: utf-8 -*-
import argparse
import numpy as np
from pprint import pprint

from PIL import Image
import matplotlib.pyplot as plt

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import grad
import torchvision
from torchvision import models, datasets, transforms


from utils import label_to_onehot, cross_entropy_for_onehot   #将标签onehot化   并使用onehot形式的交叉熵损失函数
 
parser = argparse.ArgumentParser(description='Deep Leakage from Gradients.')
parser.add_argument('--index', type=int, default="45",
                    help='the index for leaking images on CIFAR.')
parser.add_argument('--image', type=str,default="",
                    help='the path to customized image.')
args = parser.parse_args()

device = "cpu"
if torch.cuda.is_available():
    device = "cuda"
print("Running on %s" % device)

data_cifar = datasets.CIFAR100("/.torch", download=True)
To_tensor = transforms.ToTensor()
To_image = transforms.ToPILImage()

img_index = args.index



gt_data = To_tensor(data_cifar[img_index][0]).to(device)  #image_index[i][0]表示的是第I张图片的data，image_index[i][1]表示的是第i张图片的lable


if len(args.image) > 1:    #得到预设参数的图片并将其转换为tensor对象
    gt_data = Image.open(args.image)
    gt_data = To_tensor(gt_data).to(device)


gt_data = gt_data.view(1, *gt_data.size())


gt_label = torch.Tensor([data_cifar[img_index][1]]).long().to(device)
gt_label = gt_label.view(1, )
gt_onehot_label = label_to_onehot(gt_label)

plt.imshow(To_image(gt_data[0].cpu()))

from models.vision import LeNet,  ResNet18
net = LeNet().to(device)


torch.manual_seed(1234)

#net.apply(weights_init)
criterion = cross_entropy_for_onehot  #调用损失函数

# compute original gradient 
pred = net(gt_data)
y = criterion(pred, gt_onehot_label)
dy_dx = torch.autograd.grad(y, net.parameters())   #获取对参数W的梯度

original_dy_dx = list((_.detach().clone() for _ in dy_dx))    #对原始梯度复制

# generate dummy data and label
dummy_data = torch.randn(gt_data.size()).to(device).requires_grad_(True)
dummy_label = torch.randn(gt_onehot_label.size()).to(device).requires_grad_(True)

plt.imshow(To_image(dummy_data[0].cpu()))

optimizer = torch.optim.LBFGS([dummy_data, dummy_label])


history = []
for iters in range(300):
    def closure():
        optimizer.zero_grad()  #梯度清零

        dummy_pred = net(dummy_data) 
        dummy_onehot_label = F.softmax(dummy_label, dim=-1)
        dummy_loss = criterion(dummy_pred, dummy_onehot_label) 
        dummy_dy_dx = torch.autograd.grad(dummy_loss, net.parameters(), create_graph=True)   #faked数据得到的梯度
        
        grad_diff = 0
        for gx, gy in zip(dummy_dy_dx, original_dy_dx): 
            grad_diff += ((gx - gy) ** 2).sum()   #计算fake梯度与真实梯度的均方损失
        grad_diff.backward()    #对损失进行反向传播    优化器的目标是fake_data, fake_label
        
        return grad_diff
    
    optimizer.step(closure)
    if iters % 10 == 0: 
        current_loss = closure()
        print(iters, "%.4f" % current_loss.item())
        history.append(To_image(dummy_data[0].cpu()))

plt.figure(figsize=(12, 8))
for i in range(30):
    plt.subplot(3, 10, i + 1)
    plt.imshow(history[i])
    plt.title("iter=%d" % (i * 10))
    plt.axis('off')

plt.show()

这篇论文的核心就是构建一个损失函数——自己创建的一个fake的（dummy_data,dummy_label）所得到的梯度与原始训练数据（True_data,True_label）所得到的梯度的均方误差，再用损失函数对（dummy_data,dummy_label）最优化，不断迭代以恢复出原始数据

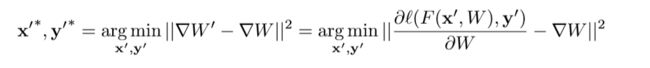
原文再cifar100数据集迭代了差不多100次才能恢复出原始数据，而我参考的这个代码很快就迭代完成了，也不知道原文的源代码是怎样写的，后续再仔细研究一下这个代码。

参考：
代码地址： https://github.com/mit-han-lab/dlg
文献地址：https://papers.nips.cc/paper/9617-deep-leakage-from-gradients.pdf