计算机视觉基础知识复习
计算机视觉
- CV01-introduction
-
- 取样和量化####
- 图像表达
- 像素基本关系
-
- m邻接定义:
- CV03-image preprocessing
-
- 代数运算
-
- 加法:
- 减法:
- 逻辑运算
- 几何运算####
-
- 空间变换
- 灰度插值
- 灰度映射
-
- 基本灰度变换函数###
- 直方图修正###
-
- 直方图均衡化###
- 直方图规定化
- 局部增强
- CV4-1 Filters(spatial domain)
-
- 平滑线性滤波器###
-
- 高斯滤波
- 识别与匹配
- 消除噪音-中值滤波(非线性)
- 锐化空间滤波###
-
- 基本的高通滤波##
- 边缘检测
- 导数滤波器###
- 梯度图像
- 一阶导数的使用-渐变###
- 二阶导数的使用-拉普拉斯算子###
- 去噪卷积
- 高斯拉普拉斯算子
- 阈值转换法
- CV 04-2频率域滤波
-
- 傅里叶变换###
- 二维离散傅里叶变换的一些性质###
- 频域滤波原理###
-
- 陷波滤波器
- 低通滤波器###
- 高通滤波器
- 同态滤波
- 局部增强
- CV05-噪声
-
- 噪声模型###
-
- 高斯噪声模型##
- 瑞利(Rayleigh) 噪声##
- 伽马指数均匀脉冲##
- 噪声分布参数的估计
- 噪声滤波去除###
-
- 均值滤波##
- 统计排序##
- 自适应(adaptive) 局部噪声消除滤波器
- 自适应(Adaptive) 中值滤波器##
- 周期噪声的降噪
- CV06-形态学处理
-
- 集合论基本知识
- 膨胀###
-
- 矩阵的膨胀
- 图像的膨胀
- 膨胀应用
- 腐蚀###
-
- 腐蚀膨胀运算公式
- 腐蚀举例
- 开操作
- 闭操作
- 开操作闭操作的应用举例
-
- 形态学主要应用###
-
- 边界提取##
- 区域填充##
- 连通分量的提取
- CV07-图像分割
-
- 基于连续性的
- 基于阈值
-
- 全局阈值处理
- 各种阈值处理
- 聚类方法
-
- K-means
- Mean Shift
- 反向投影图
- 基于区域的方法#####
-
- region growing###
- 主动轮廓模型###
- CV08-局部特征
-
- 边缘检测器###
-
- Canny edge detector####
- 边缘像素连接
- 边界细化###
- 寻找角落
-
- SUSAN算子
- Harris兴趣点算子###
- Automatic Scale Selection
- Hough 变换###
- CV09-图像表示与描述
-
- 区域描述符
-
- 拓扑描述符###
- 纹理
- 不变矩###
- 使用主要成分进行描述####
- CV10-纹理
-
- 与纹理有关的任务
- 灰度共生矩阵###
- 基于共生矩阵的描述###
-
- 各种描述量
- 应用
- 基于能量的描述###
- 双目视觉
-
- 三个坐标系
- 基本原理
- 具体实现
CV01-introduction
取样和量化####
取样,对坐标数字化,决定像素多少,决定图像空间分辨率
量化,对幅度数字化,决定像素灰度值等级 eg:量化为256级图像有8bit灰度分辨率
量化决定了图像中对比度变化的“平滑”程度更精细的量化将防止“假轮廓”(人造边缘)–较粗糙的量化可压缩图像
图像表达
矢量表示 仅描述相对高级的图形结构,例如直线,圆弧,圆形等;
位图表示:分别描述和存储图像中的每个像素值
像素基本关系
邻接:对两个像素p和q来说,如果q在p的邻域中,则称p和q满足邻接关系
连接:p和q邻接且灰度值均满足某个特定的相似准则(V,一个灰度值集合,像素值再V中)
连通 :不(直接)邻接,但均在另一个像素的相同邻域中,且这3个像素的灰度值均满足某个特定的相似准则
通路,连通分量,连通集
m邻接定义:
对于V 假设要p,q两点是m邻接的 则要满足下面两个条件之一即可:
- q在p的4邻域中。
- q在p的对角领域中,并且q的4邻域与p的4领域相交为空集(交集无点属于V)。
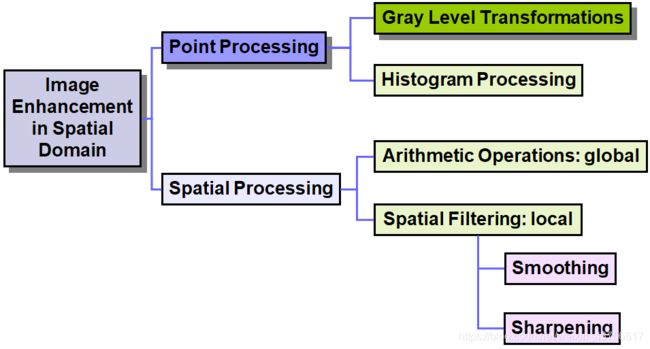
CV03-image preprocessing
代数运算
是指对图像象素 几何不变化 ,图像 灰度级的 加、减、乘和除运算 。也就是对两幅输入图像进行pixel-by-pixel 的加、减、乘和除计算而得到输出图像 的运算
加法:
Image Composite (合成): C = α F + ( 1 − α ) B \text { Image Composite (合成): } C=\alpha F+(1-\alpha) B Image Composite (合成): C=αF+(1−α)B
减法:
Diff ( x , y ) = ∥ I ( x , y ) − B ( x , y ) ∥ 2 \operatorname{Diff}(x, y)=\|I(x, y)-B(x, y)\|^{2} Diff(x,y)=∥I(x,y)−B(x,y)∥2
Is foreground if Diff ( x , y ) > T (x, y)>T (x,y)>T (a given threshold)
R n ′ ( x , y ) = { 255 , D n ( x , y ) > T 0 , else ht tp: / / b R_{n}^{\prime}(x, y)=\left\{\begin{array}{l} 255, D_{n}(x, y)>T \\ 0, \text { else ht tp: } / / b \end{array}\right. Rn′(x,y)={255,Dn(x,y)>T0, else ht tp: //b
在背景维持不变的环境下,对运动目标检测:
1.去除图像相同位置数据中的最大值和最小值,然后取均值的方法 获得背景图像。
2. 将图像与背景图 做差值计算, 获得图像差图。
3. 采用二维自适应 维纳滤波对差值图形滤波 减小噪声影响。
4. 将滤波后差值图,设定阈值进行二值化,同时 采用形态学的腐
蚀膨胀, 使二值图像中 目标轮廓边缘更加平滑,减小图像内部
空隙,符合实际目标。
逻辑运算
注意灰度值的并集和交集操作与二值图像不同,不要单纯想做01布尔运算
几何运算####
经过几何变换改变像素空间关系,产生几何失真,需要几何失真校正:
空间变换
用它来描述每个像素如何从其初始位置“移动”到终止位置;
要求保持图像中曲线型特征的 连续性 和各物体的 连通性
g ( x , y ) = f ( x ′ , y ′ ) = f [ a ( x , y ) , b ( x , y ) ] g(x, y)=f\left(x^{\prime}, y^{\prime}\right)=f[a(x, y), b(x, y)] g(x,y)=f(x′,y′)=f[a(x,y),b(x,y)]
灰度插值
目标图像的点除以rate映射回到原图像点,但该点不在像素点上,像素值由插值得出
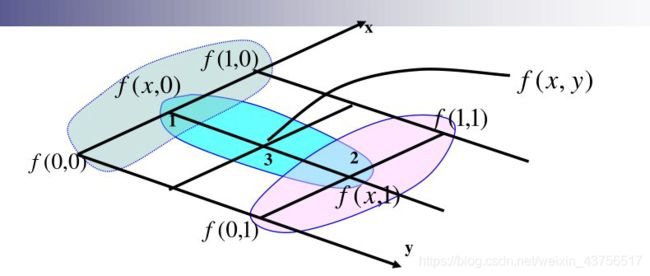
灰度映射
基本灰度变换函数###
图像反转:适用增强嵌入图像暗色区域中的白色或灰色细节,例如医学图像
对数变换:动态范围压缩(想象一下,x轴的0-10被压缩到y轴0-1),扩展暗像素值,压缩高亮像素值 (适用范围:图像灰度动态范围过大,超过图像显示装备范围)P65
伽马变换:gamma<1可以用来当监视器,使暗的变亮
那个伽马图像越大曲线越在下面
分段线性函数:1.对比度拉伸:对比度增强,阈值处理
2.灰度级分层,使感兴趣的灰度区域显示为一个值,增强某些特征
二值化方法之一:isodata 算法
◆ 1. 选初始阈值T0,该值把图像分成了两部分R1,R2
◆ 2. 求R1的灰度平均值u1,R2的灰度平均值u2,新的二值化阈值Ti=(u1+u2)/2,又分成两部分,再求u1和u2的均值,迭代直到Ti的值没有变化
二值化方法之二:Otsu 算法(最大类间方差法)
聚类的思想:把图像的灰度数按灰度级分成2个部分,使得两个部分之间的灰度值差异最大,每个部分之间的灰度差异最小,通过计算 方差来寻找一个合适的灰度级别来划分
位平面切片
直方图修正###
应用1 :阈值化
应用2 :视频镜头分割(不同场景直方图差距大)
直方图均衡化###
直方图规定化
SML:原始累计直方图的矩阵右边连规定累积直方图矩阵右边,哪个短选哪个,由原始映射到规定
GML:规定 矩阵右边先垂直做线,对垂直线两边原始矩阵边划线,选短的。由规定包括原始
局部增强
CV4-1 Filters(spatial domain)
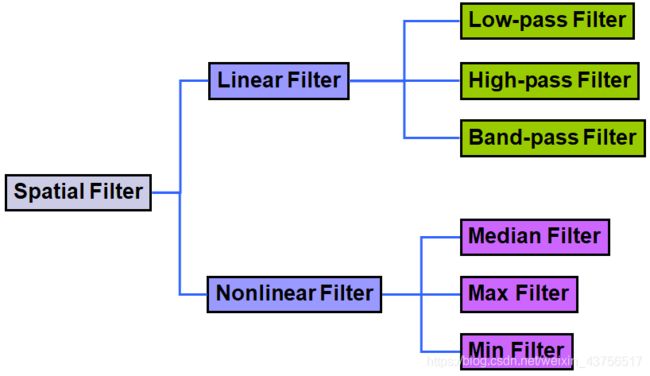
平滑线性滤波器###
均值滤波,用于降低噪声,但是会边缘模糊。主要用于去除图像中不相关细节,不相关:尺寸比滤波器小。
高斯滤波
二维空间 高斯函数 是等高线从中心成正态分布的同心圆
p ( z ) = 1 2 π σ e − ( z − μ ) / 2 σ 2 p(z)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-(z-\mu) / 2 \sigma^{2}} p(z)=2πσ1e−(z−μ)/2σ2
均值标准差
◆ 分布不为零的点组成卷积阵与原始图像做变换,即每个像素值是周围相邻像素值的高斯平均。
◆ 在大概3σ 距离之外的像素都可以看作不起作用,这些像素的计算也就可以忽略。
G ( x , y ; σ ) = 1 2 π σ 2 e − x 2 + y 2 2 σ 2 G(x, y ; \sigma)=\frac{1}{2 \pi \sigma^{2}} e^{-\frac{x^{2}+y^{2}}{2 \sigma^{2}}} G(x,y;σ)=2πσ21e−2σ2x2+y2
卷积:
G = H ⋆ F G=H \star F G=H⋆F
相关:
G = H ⊗ F G=H \otimes F G=H⊗F
- 过滤器是可分离的,我们可以分为两个步骤:–卷积所有行–卷积所有列
二维高斯函数卷积可分两步进行:首先将图像与一维高斯函数卷积,
然后将卷积结果与方向垂直的相同一维高斯函数卷积。因此,二维
高斯函数的计算量随模板宽度成线性增长而不是成平方增长,所以
较大尺寸的高斯滤波器可以得以有效的实现
识别与匹配
消除噪音-中值滤波(非线性)
主要用于降噪◼消除椒盐噪声
对高斯噪声非常有效
对Impulse脉冲噪声非常有效。脉冲噪声(impulsive noise)是非连续的,由持续时间短和幅度大的不规则脉冲或噪声尖峰组成
锐化空间滤波###
目的:突出精细的细节
锐化:差异:增强边缘并强调缓慢变化的区域
基本的高通滤波##
滤波器的中心附近应具有正系数,而外围应具有负系数。
滤波器越大,提取边缘越多越亮
边缘检测
目标:将图像从二维像素阵列映射到一组曲线或线段或轮廓。
主要思想:寻找强梯度,后处理
导数滤波器###
First derivative
f ′ ( x ) = f ( x + 1 ) − f ( x ) f^{\prime}(x)=f(x+1)-f(x) f′(x)=f(x+1)−f(x)
Second derivative
f ′ ′ ( x ) = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) f^{\prime \prime}(x)=f(x+1)+f(x-1)-2 f(x) f′′(x)=f(x+1)+f(x−1)−2f(x)
对于一阶微分的任何定义都必须保证满足:
1.在恒定区域的微分值为0
2.在灰度台阶或者斜坡开始处微分值非0
3.沿着斜坡的微分值非0
对于二阶导数:
1.在恒定区域的微分值为0
2.在灰度台阶或者斜坡起点和终点处微分值非0
3.沿着斜坡的微分值为0
一阶导数在图像中产生较厚的边缘◼二阶导数对精细的细节具有更强的响应(产生由零分开的一个像素宽双边缘)◼一阶导数对灰度阶跃具有更强的响应◼二阶导数在灰度阶跃变化时产生双重响应◼二阶导数具有对线的响应比对阶跃强 和对点的响应要强于对线的响应
灰度阶跃:a,b两像素相邻,a像素值为1,b像素值蹦到了255
梯度图像
P102
一阶导数的使用-渐变###
提取边缘
图像处理中最常见的微分方法是梯度
非各向同性◼其大小(通常称为梯度)是旋转不变的
下面的算子都是勾成了梯度图像
用这个图想象一下,怎么求边缘的
5 5 5 5 10 10 10 10 5 5 5 5 10 10 10 10 5 5 5 5 10 10 10 10 5 5 5 5 10 10 10 10 5 5 5 5 10 10 10 10 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 \begin{array}{llllllll}5 & 5 & 5 & 5 & 10 & 10 & 10 & 10 \\ 5 & 5 & 5 & 5 & 10 & 10 & 10 & 10 \\ 5 & 5 & 5 & 5 & 10 & 10 & 10 & 10 \\ 5 & 5 & 5 & 5 & 10 & 10 & 10 & 10 \\ 5 & 5 & 5 & 5 & 10 & 10 & 10 & 10 \\ 5 & 5 & 5 & 5 & 5 & 5 & 5 & 5 \\ 5 & 5 & 5 & 5 & 5 & 5 & 5 & 5 \\ 5 & 5 & 5 & 5 & 5 & 5 & 5 & 5\end{array} 555555555555555555555555555555551010101010555101010101055510101010105551010101010555
◆Roberts运算符 ###
用罗伯特梯度算子运算的实质是交叉地求对角方向象素之间灰度差的和,作为该象素的值。对一幅图象从左到右,从上到下扫描遍,求出各点梯度产生梯度图象达到突出边缘的目的。
但是由于采用偶数模板,如下图所示,所求的(x,y)点处梯度幅度值其实是图中交叉点处的值,从而导致在图像(x,y)点处梯度幅度值偏移了半个像素
◆Prewitt运算符 ####
利用像素点上下、左右邻点灰度差,在边缘处达到极值检测边缘。对噪声具有平滑作用,定位精度不够高。
◆Sobel运算符####
Sobel算子利用像素点上下,左右邻点的灰度加权算法,根据在边缘点出达到极值这一现象进行边缘的检测。 Sobel算子对噪声具有平滑作用,提供较为精确的边缘方向信息,但它同时会检测出许多的伪边缘,边缘定位精度不高。当对精度要求不是很高时,是一种较为常用的方法。
二阶导数的使用-拉普拉斯算子###
各向同性过滤器:旋转不变
Laplacian (linear operator):
∇ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \nabla^{2} f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}} ∇2f=∂x2∂2f+∂y2∂2f
Discrete version:
∂ 2 f ∂ 2 x 2 = f ( x + 1 , y ) + f ( x − 1 , y ) − 2 f ( x , y ) ∂ 2 f ∂ 2 y 2 = f ( x , y + 1 ) + f ( x , y − 1 ) − 2 f ( x , y ) \begin{array}{l} \frac{\partial^{2} f}{\partial^{2} x^{2}}=f(x+1, y)+f(x-1, y)-2 f(x, y) \\ \frac{\partial^{2} f}{\partial^{2} y^{2}}=f(x, y+1)+f(x, y-1)-2 f(x, y) \end{array} ∂2x2∂2f=f(x+1,y)+f(x−1,y)−2f(x,y)∂2y2∂2f=f(x,y+1)+f(x,y−1)−2f(x,y)
拉普拉斯应用于灰度突变区域,产生暗色背景中叠加有浅灰色边线和突变点的图像,将原图像和拉普拉斯图像叠加或者减去可以复原背景特性并保持锐化处理。(看中心点的正负值)
去噪卷积
卷积的导数定理: ∂ ∂ x ( h ⋆ f ) = ( ∂ ∂ x h ) ⋆ f \frac{\partial}{\partial x}(h \star f)=\left(\frac{\partial}{\partial x} h\right) \star f ∂x∂(h⋆f)=(∂x∂h)⋆f
h为卷积核函数,f为原图像灰度函数
高斯拉普拉斯算子
阈值转换法
CV 04-2频率域滤波
傅里叶变换###
F ( u ) = ∫ x = − ∞ ∞ f ( x ) e − 2 j π u x d x F(u)=\int_{x=-\infty}^{\infty} f(x) e^{-2 j \pi u x} d x F(u)=∫x=−∞∞f(x)e−2jπuxdx
傅立叶变换
and
f ( x ) = ∫ u = − ∞ ∞ F ( u ) e 2 j π u x d u f(x)=\int_{u=-\infty}^{\infty} F(u) e^{2 j \pi u x} d u f(x)=∫u=−∞∞F(u)e2jπuxdu
傅立叶逆变换
离散:
F ( u ) = 1 M ∑ x = 0 M − 1 f ( x ) e − 2 j π u x / M F(u)=\frac{1}{M} \sum_{x=0}^{M-1} f(x) e^{-2 j\pi{ux} / M} F(u)=M1x=0∑M−1f(x)e−2jπux/M
and
f ( x ) = ∑ u = 0 M − 1 F ( u ) e 2 j π u x / M f(x)=\sum_{u=0}^{M-1} F(u) e^{2 j \pi u x / M} f(x)=u=0∑M−1F(u)e2jπux/M
&&傅里叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数;傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数
求出F(u,v)后算实部虚部平方和就是对应值(傅里叶频谱)
公式一: 设 α \alpha α 为任意角, π + α \pi+\alpha π+α 与 α \alpha α 的三角函数值之间的关系:
sin ( π + α ) = − sin α cos ( π + α ) = − cos α tan ( π + α ) = tan α cot ( π + α ) = cot α \begin{aligned} \sin (\pi+\alpha) &=-\sin \alpha \\ \cos (\pi+\alpha) &=-\cos \alpha \\ \tan (\pi+\alpha) &=\tan \alpha \\ \cot (\pi+\alpha) &=\cot \alpha \end{aligned} sin(π+α)cos(π+α)tan(π+α)cot(π+α)=−sinα=−cosα=tanα=cotα
公式二: 任意角 − α -\alpha −α 与 α \alpha α 的三角函数值之间的关系:
sin ( − α ) = − sin α cos ( − α ) = cos α tan ( − α ) = − tan α cot ( − α ) = − cot α \begin{aligned} \sin (-\alpha) &=-\sin \alpha \\ \cos (-\alpha) &=\cos \alpha \\ \tan (-\alpha) &=-\tan \alpha \\ \cot (-\alpha) &=-\cot \alpha \end{aligned} sin(−α)cos(−α)tan(−α)cot(−α)=−sinα=cosα=−tanα=−cotα
二维离散傅里叶变换的一些性质###
在频率域图里,亮的地方代表这个地方响应幅度大,比如图像中心亮,原图中对应低频之类的多
∣ F ( u ) ∣ = [ R 2 ( u ) + I 2 ( u ) ] 1 / 2 ϕ ( u ) = tan − 1 [ I ( u ) R ( u ) ] |F(u)|=\left[R^{2}(u)+I^{2}(u)\right]^{1 / 2} \quad \phi(u)=\tan ^{-1}\left[\frac{I(u)}{R(u)}\right] ∣F(u)∣=[R2(u)+I2(u)]1/2ϕ(u)=tan−1[R(u)I(u)]
Fourier spectrum 傅立叶谱(频谱) Phase angle (相角)
P148
1.移中处理:将F ( 0 , 0 ) (\mathbf{0}, \mathbf{0}) (0,0) 移动到 F ( M / 2 , N / 2 ) \mathrm{F}(\mathrm{M} / 2, \mathrm{~N} / 2) F(M/2, N/2)
I [ f ( x , y ) ( − 1 ) x + y ] = F ( u − M / 2 , v − N / 2 ) \mathfrak{I}\left[f(x, y)(-1)^{x+y}\right]=F(u-M / 2, v-N / 2) I[f(x,y)(−1)x+y]=F(u−M/2,v−N/2)
2.说明:傅立叶变换对加法有分配率,但对乘法没有
例如 g ( x , y ) = f ( x + 1 , y ) − f ( x , y ) \text { 例如 } \quad \mathrm{g}(x, y)=f(x+1, y)-f(x, y) 例如 g(x,y)=f(x+1,y)−f(x,y)
对其进行傅立叶变换得:
G ( x , y ) = I { f ( x + 1 , y ) } − I { f ( x , y ) } G(x, y)=\mathfrak{I}\{f(x+1, y)\}-\mathfrak{I}\{f(x, y)\} G(x,y)=I{f(x+1,y)}−I{f(x,y)}
3.平移 PPT71
4.缩放 PPT72
以下性质不考 。。吧
5.旋转 PPT100
6.周期性和共轭对称性(这个不会)
7.傅立叶谱|F(u, v)| ,可以对其作为图像强度来显示,图像 亮度正比于幅度
幅度谱常常具有巨大的 动态范围 0 –2,500,000
仅仅 最亮 的部分频谱可见
因此,对其进行 对数变换 ,可以提高其细节的显示能力
8.可分离性
先对某一列求出傅里叶变换,再对F(x,v)进行一整行的傅里叶变换
9.卷积理论
傅立叶变换对的卷积定理:
f ( x ) ∗ g ( x ) ⇔ F ( u ) G ( u ) f ( x ) g ( x ) ⇔ F ( u ) ∗ G ( u ) \begin{array}{l} f(x)^{*} g(x) \Leftrightarrow F(u) G(u) \\ f(x) g(x) \Leftrightarrow F(u)^{*} G(u) \end{array} f(x)∗g(x)⇔F(u)G(u)f(x)g(x)⇔F(u)∗G(u)
10.快速傅里叶变换
ppt113
频域滤波原理###
◼1. 对输入图像乘以(-1) (x+y) 以对图像进行移中
◼ 2. 对1 的结果进行二维离散傅立叶变换(DFT) ,计算F(u,v)
◼ 3. 对F(u,v) 乘上滤波函数H(u,v)
◼ 4. 对3 的结果进行离散傅立叶逆变换
◼ 5. 取4 的结果的实部
◼ 6. 对5 的结果乘上(-1) (x+y) 获得空域的滤波后图像
例子:ppt124 注意:此时频率域矩形的中心已经变为了(M/2,N/2)
一个频率域图,中心点是矩阵的中心,不是左下角(0,0)
陷波滤波器
◼滤出一定范围的“有害”频率
◼不影响图像的对比度
◼防止引入高频:振铃
◼为应用而设计
eg:去除图像中的有规律的周期噪声,如一条又一条的白线
低通滤波器###
理想低通滤波器是指:
以截频D0 为半径的 圆内 的所有频率都能无损通过
以截频D0 为半径的 圆外 的所有频率分量完全被衰减
振铃效应:ppt122
同心圆环半径(Sa函数的零点)反比于截止频率 D0
D0较小, h ( x , y ) \mathbf{h}(\mathbf{x}, \mathbf{y}) h(x,y) 产生数量少但较宽的同心圆环
D0较大, h ( x , y ) \mathbf{h}(\mathbf{x}, \mathbf{y}) h(x,y) 产生数量多但较窄的同心圆环
巴特沃兹低通滤波器:
本来图象是,当x=[0,D0]时y=1,x>D0,y=0
现在是一个平滑的,逐渐下降,趋近于0,保留高通的信息
与理想低通滤波器的处理结果相比,巴特沃兹滤波器处理 的图像 模糊程度减少 ,因为它的H(u,v) 不是陡峭的截止特性,它的尾部会包含大量的高频成分。
另外经巴特沃兹低通滤波器处理的图像将 不会有振铃现象 。 这是由于在滤波器的通带和阻带之间有一平滑过渡的缘故。
- 损坏字符修复:通过模糊输入图像来弥合小间隙
- 减少眼睛周围的细纹,使平滑的图像看起来非常柔和悦目
高通滤波器
图像锐化可以通过高通滤波过程实现,该过程可以衰减低频分量而不会干扰高频信息
高通滤波器: H h p ( u , v ) = 1 − H l p ( u , v ) ( 低 通 滤 波 器 ) H_{\mathrm{hp}}(u, v)=1-H_{\mathrm{lp}}(u, v)(低通滤波器) Hhp(u,v)=1−Hlp(u,v)(低通滤波器)
高通滤波=原图像-低通滤波结果
高频提升滤波器:原始图像乘以一个放大系数A再减去低通图像
好多对比图,记得看ppt
同态滤波
同态滤波是一种在频域中同时将图像亮度范围进行压缩和将图像对比度进行增强的方法- 即把频率过滤和灰度变换结合起来
局部增强
在实际中,对某些局部信息感兴趣,其象素数量相对于整幅图像的象素数量往往较小,利用整幅图像算得的变换或转移函数并不能保证在这些局部区域能得到增强效果
直方图变换是空域增强中最常用的方法,也容易用于局部增强。
CV05-噪声
描述噪声一般采用统计意义上的均值和方差。
均值:表明了图像中噪声分布的总体强度。
方差:表明图像噪声分布的强弱差异
协方差
噪声模型###
ppt16页开始
高斯噪声模型##
电子电路噪声
高温导致的传感器噪声
暗光照导致的传感器噪声
瑞利(Rayleigh) 噪声##
适用于深度图像
不对称的直方图
伽马指数均匀脉冲##
噪声分布参数的估计
对于周期噪声,通过检测图像的傅里叶谱来估计;
从传感器的规格说明中获取;
使用一张标准图像检测成像系统的噪声参数; 利用图像本身的信息- 截取图像区域中较为平坦的一个子区域作为标准测试图像,检测噪声直方图形状,即用局部直方图进行估计;
噪声滤波去除###
均值滤波##
ppt26
Harmonic (谐波) mean filter:
f ^ ( x , y ) = m n ∑ ( s , t ) ∈ S x y 1 g ( s , t ) \hat{f}(x, y)=\frac{m n}{\sum_{(s, t) \in S_{x y}} \frac{1}{g(s, t)}} f^(x,y)=∑(s,t)∈Sxyg(s,t)1mn
对盐噪声效果更好,但不适用于椒噪声,并且善于处理高斯噪声等其他噪声
Contra-harmonic (逆谐波) mean filter: f ^ ( x , y ) = ∑ ( s , t ) ∈ S y y g ( s , t ) Q + 1 ∑ ( s , t ) ∈ S x y g ( s , t ) Q \quad \hat{f}(x, y)=\frac{\sum_{(s, t) \in S_{y y}} g(s, t)^{Q+1}}{\sum_{(s, t) \in S_{x y}} g(s, t)^{Q}} f^(x,y)=∑(s,t)∈Sxyg(s,t)Q∑(s,t)∈Syyg(s,t)Q+1
逆谐波均值滤波器:适用于椒盐噪声,但不能同时消除:当Q>0 时消除椒噪声;当Q<0 时消除盐 噪声;当Q=0 时退化为算术均值滤波;当Q=-1 时退化为谐波均值滤波
统计排序##
ppt30
中值滤波同时去除椒盐噪声可以多次重复滤波
自适应(adaptive) 局部噪声消除滤波器
自适应:系统根据当前自身的状态和环境调整自身的参数以达到预先设定的目标
◼ 自适应滤波器是基于m×n 的矩形窗口Sxy定义的区域内图像的统计特征而变化的。----- 退化图像= 原图像+ 噪声
自适应(Adaptive) 中值滤波器##
基本思想
中值滤波器的尺寸如果太小,可以较好地保护图像的某些细节,但往往遗漏噪声;多次滤波造成特征丧失、图像模糊
反之,如果太大的话,可以加强噪声抑制能力,但图像会很模糊, 有时候会滤去图像中的一些细线、尖锐边角等重要细节,从而破坏 图像的几何结构
因此,先采用小尺寸的中值滤波;当发现滤波器不够好时,扩大其尺寸,再次滤波;再不好;再扩大,直到达到最大尺寸
这个策略称为 自适应 的策略
总体来说,先小滤波保护图像细节,发现滤波结果如果是脉冲就扩大。
周期噪声的降噪
与频率域图像增强相比,图像恢复采用更加 专用 的频率域 低通和高通滤波器,用以减弱或消除周期噪声
带通
带阻
陷波滤波器
CV06-形态学处理
基本思想:是用具有一定形态的结构元素去度量和提取图像中的对应形状以达到对图像分析和识别的目的
图像处理的 基本运算有4 个: 膨胀、腐蚀、开操作和闭操作
集合论基本知识
反射:关于 原集合 原点对称
平移
集合关系:包含,击中,击不中
膨胀###
B 的反射进行平移z 与A 的交集不为空
膨胀以模板的中心为关键,中心要在要膨胀的图像里
矩阵的膨胀
图像的膨胀
膨胀应用
桥接文字裂缝
优点:可在一幅二值图像中直接得到结果,可与低通滤波方法对比
腐蚀###
腐蚀膨胀运算公式
ppt19
腐蚀举例
- 用腐蚀的方法去掉不同粗细的区域(去掉图像中一些细小的线)
- 使用腐蚀消除图像的细节部分,产生滤波器的作用(去除小噪声)
开操作
含义: 先用B 对A 腐蚀,然后用B 对结果膨胀
在不改变形状的前提下,使图像的轮廓变得光滑
断开狭窄的间断
消除细的突出物
闭操作
含义: 先用B 对A 膨胀,然后用B 对结果腐蚀
在不明显改变面积前提下,使图像的轮廓变得光滑
弥合狭窄的间断和细长的鸿沟
消除小的孔洞
填补轮廓线中的裂痕
开操作闭操作的应用举例
说明:先开操作再闭操作,构成噪声滤波器
指纹操作,ppt42
形态学主要应用###
边界提取##
先用B 对A 腐蚀,然后用A 减去腐蚀得到 ,B 是结构元素 SE、
区域填充##
定义起点为区域内空白区域内一点,对该点开始进行膨胀,然后与A补相交的点留下,循环,知道最后收敛。再与A相交,则区域填充完毕
连通分量的提取
CV07-图像分割
图像分割是把图像分成各具特性的区域,并提取出感兴趣目标的技术和过程。这里特性可以是灰度、颜色、纹理等,目标可以对应单个区域,也可以对应多个区域。
基于连续性的
基于阈值
适用于物体与背景有较强对比的情况,重要的是背景或物体的灰度比较单一;
–这种方法总可以得到封闭且连通区域的边界
阈值分割方法的关键是: 选取合适的阈值T
◆全局阈值:仅根据各图像像素的本身性质f(x,y)来选取而得到的阈值
◆局部阈值:根据像素的本身性质f(x,y)和像素周围局部区域性质q(x,y)来选取而得到的阈值
◆动态阈值:根据像素的本身性质f(x,y)、像素周围局部区域性质q(x,y)和像素位置坐标(x,y)来选取
全局阈值处理
ppt17 迭代算法
Otsu 算法( 聚类的思想) :把图像的灰度数按灰度级分成2个部分,
使得两个部分之间的灰度值差异最大,每个部分之间的灰度差
异最小,通过计算 方差来寻找一个合适的灰度级别来划分
各种阈值处理
直方图,动态阈值
聚类方法
空间聚类:将图像空间中的元素按照从测得的特征值对应的特征空间点表示,通过将特征空间的点聚集成对应不同区域的类团,从而将它们划分开,然后再反映射回到原图像空间就得到分割的结果。
K-means
eg:真彩色降维低彩色
将好多颜色聚类成一类颜色
Mean Shift
ppt31
反向投影图
基于区域的方法#####
区域:
基本定义–一组具有相似属性的相连像素
通常通过使用图像像素的灰度值来划分为区域。
两种通用方法–基于区域的分割–使用边缘检测的边界估计
region growing###
将一组种子与图像一起作为输入
•通过将所有未分配的相邻像素与区域进行比较来迭代生长区域
算法实现:
–根据图像的特点选择一个或一组种子,最亮、最暗或位于点簇中心的点;
–选择一个描述符(条件,如特定范围内的灰度或颜色)
–从种子开始向外扩张,首先把种子像素加入结果集,然后不断将与结果集中各个像素连通、且满足描述符的像素加入集合
–上述过程进行到不再有满足条件的新节点加入集合为止
要解决3个问题:
–确定区域数目
–选择有意义的特征(灰度、纹理、颜色)
–确定相似性准则
主动轮廓模型###
主动轮廓模型基本思想:使用连续曲线来表达目标边缘,并定义一个能量泛函使得其自变量包括边缘曲线,因此分割过程就转变为求解能量泛函的最小值的过程,一般可通过求解函数对应的欧拉( Euler. Lagrange)方程来实现,能量达到最小时的曲线位置就是目标的轮廓所在
具体方法:
• 首先通过人的识别能力,在待提取轮廓的附近设置若干控制点并连成一条连续曲线;
• 然后充分利用图像信息、外部限制及曲线连续性和平滑性的限制定义一个能量函数,作用于各个控制点,使控制点向使能量函数最小的区域移动,当能量函数不再减小时即得到要求提取的轮廓;
• 曲线在移动的过程中是一种扭曲蠕动的方式,所以又称为snake。
E = ∫ [ α ( s ) E cont + β ( s ) E curv + γ ( s ) E image ] d s E=\int\left[\alpha(s) E_{\text {cont}}+\beta(s) E_{\text {curv}}+\gamma(s) E_{\text {image}}\right] d s E=∫[α(s)Econt+β(s)Ecurv+γ(s)Eimage]ds
上式中,通常 α \alpha α大,轮廓收敛越快; β \beta β越大,轮廓越光滑。调整 α \alpha α和 β \beta β的大小,可以调整曲线的斜率和曲率对曲线影响的大小,从而使轮廓曲线收 敘到图像中比较合理的位置。
内部能量函数: Eint(vi)是依赖于轮廓形状的能量函数。推动主动轮廓形状的改变并保持轮廓上点间的距离。包括:Econ:连续能量(切向力),迫使不封闭的曲线变成直线而封闭的曲线变成圆环。
Ebal :膨胀能量(法向力),强制轮廓在没有外来影响的情况下扩展或收缩。
外部能量函数:Eext(vi)是依赖于图象性质的能量函数。
将变形模板向感兴趣的特征(如边缘)吸引构建能量函数:考虑目标的尺寸和形状。包括:Emag: 图象灰度能量:将轮廓吸向高或低的灰度区域
Egard:图象梯度能量将轮廓推向特征(边缘)。
CV08-局部特征
通常情况下,将图像的多种特征组合在起,形成一个n维特征向量来表示该图像。
该n维特征向量就是一个位于n维空间中的点,而图像识别的任务就是找到对这个n维空间的一种划分,使该类图像与其他类图像在空间上分开。
选择的特征不仅要能够很好地描述图像,更重要的是能够很好地区分不同类别的图像。
我们希望选择那些在同类图像之间差别较小(较小的类内距),在不同类别的图像之间差异较大(较大的类间距)的图像特征。
边缘检测器###
Canny edge detector####
ppt21
使用高斯导数过滤图像
•查找梯度的大小和方向
•非最大抑制:–细化多像素宽的“脊”,直至单个像素宽度
•链接和阈值(滞后):
–定义两个阈值:低和高
–使用高阈值开始边缘曲线,使用低阈值继续边缘曲线
•抑制孤立的弱边缘
边缘像素连接
• 目的:对做过边缘检测的图像进行,目的是连接间断的边
• 方法:对每个边缘点(x,y)的邻域内像素的特点进行分析
边界细化###
模板的非最大抑制
⚫ 计算当前像素点的梯度方向,选择相应模板;
⚫ 观察所选模板覆盖的两个相邻像素的梯度方向,如果和当前像素
差很大(如大于90°)则不能用它们来细化当前像素所在的边缘;
⚫ 根据模板指定的邻域像素判断本像素点是否是最大梯度;
⚫ 非最大梯度,则本点为非边界点,消除
插值非最大抑制
目的:找出在一个像素点上最能吻合其所在梯度方向的两侧的像素值。
方法:通过对相邻单元的梯度幅度的插值来在当前位置的周围估计梯度的幅度;
寻找角落
关键特性:在拐角处的区域中,图像梯度具有两个或多个主要方向
SUSAN算子
Harris兴趣点算子###
黑本P80
角点作为独特的兴趣点
E ( u , v ) = ∑ x , y ⟩ w ( x , y ) [ I ( x + u , y + v ) − I ( x , y ) ] 2 E(u, v)=\sum_{x, y\rangle} w(x, y)[I(x+u, y+v)-I(x, y)]^{2} E(u,v)=x,y⟩∑w(x,y)[I(x+u,y+v)−I(x,y)]2
H = [ ∑ I x I x ∑ I x I y ∑ I x I y ∑ I y I y ] = ∑ [ I x I y ] [ I x I y ] H=\left[\begin{array}{cc} \sum I_{x} I_{x} & \sum I_{x} I_{y} \\ \sum I_{x} I_{y} & \sum I_{y} I_{y} \end{array}\right]=\sum\left[\begin{array}{c} I_{x} \\ I_{y} \end{array}\right]\left[\begin{array}{ll} I_{x} I_{y} \end{array}\right] H=[∑IxIx∑IxIy∑IxIy∑IyIy]=∑[IxIy][IxIy]
H = [ ∑ I x 2 ∑ I x I y ∑ I x I y ∑ I y 2 ] = [ λ 1 0 0 λ 2 ] H=\left[\begin{array}{cc} \sum I_{x}^{2} & \sum I_{x} I_{y} \\ \sum I_{x} I_{y} & \sum I_{y}^{2} \end{array}\right]=\left[\begin{array}{cc} \lambda_{1} & 0 \\ 0 & \lambda_{2} \end{array}\right] H=[∑Ix2∑IxIy∑IxIy∑Iy2]=[λ100λ2]
角点响应函数:
R = det ( H ) − k trace ( H ) 2 = λ 1 λ 2 − k ( λ 1 + λ 2 ) 2 R=\operatorname{det}(H)-k \operatorname{trace}(H)^{2}=\lambda_{1} \lambda_{2}-k\left(\lambda_{1}+\lambda_{2}\right)^{2} R=det(H)−ktrace(H)2=λ1λ2−k(λ1+λ2)2
k: constant (0.04 to 0.06)
R为大数值 正时检测到的是 角点;
R为大数值 负时检测到的是 边;
R很 小时检测到的是 平坦区域
Automatic Scale Selection
Hough 变换###
基本霍夫变换
◆ (1) 对参数空间中参数p和q的可能取值范围进行量化,根据量化结果构造一个累加数组A(pmin: pmax, qmin: qmax),并初始化为零。( p是XY空间直线的斜率; q是直线的
截距)
◆(2) 对每个XY空间中的给定点让p取遍所有可能值,用式y=p*x+q (4.4.2)计算出q,根据p和q的值累加A,即A(p, q)= A(p, q) + 1。
◆(3) 根据累加后A中最大值所对应的p和q,由式q=-px+y确定出XY中的一条直线
直线的每个点都满足某方程(kb是直线方程,p θ \theta θ是直线法线方程),道理都一样,在参数空间里让kb(或者p θ \theta θ)作为坐标轴,对每个(x,y)作为“参数”,求出的图像共点(k,b)(或者(p, θ \theta θ)
CV09-图像表示与描述
目的:以比图像本身更合适的其他形式表示和描述嵌入图像的信息
我们可以使用哪种信息? -边界,形状-区域-纹理-区域之间的关系
6.1.1 Boundary (Border) Following
6.1.2 Chain Codes
4方向链码: ( 5 , 5 ) 111232323000 \text { 4方向链码: } \quad(5, \quad 5) 111232323000 4方向链码: (5,5)111232323000
形式:开头是起始坐标,记住最后一个0代表回到起始点
码串太长,噪声干扰:通过选择较大的网格间距对边界重新采样。
链式代码的第一个区别:计算代码中两个相邻元素之间(逆时针)方向改变的次数
6.1.3 Polygonal Approximations Using Minimum-
Perimeter Polygons多边形逼近——MPP
6.1.4 Other Polygonal Approximation Approaches
6.1.5 Signatures
6.1.6 Boundary Segments
6.1.7 Skeletons
区域描述符
拓扑描述符###
◆该区域的孔数; H
◆-连接的组件数; C
欧拉数:E=C-H
纹理
不变矩###
参考网址
若将m0看作是图像的灰度质量,则(i,j)为图像的质心坐标,那么中心矩p反映的是图像灰度相对于其灰度质心的分布情况。
不变矩:独立于旋转,平移,缩放和反射
在这里插入图片描述
使用主要成分进行描述####
目的:减少矢量图像的维数,同时尽可能保留信息
主成分分析步骤如下:
①计算输入的高维信号的协方差矩阵;
根据公式:
C x = 1 M ∑ k = 1 M x k x k T − m x m x T \boldsymbol{C}_{\boldsymbol{x}}=\frac{1}{M} \sum_{k=1}^{M} \boldsymbol{x}_{k} \boldsymbol{x}_{k}^{\mathrm{T}}-\boldsymbol{m}_{\boldsymbol{x}} \boldsymbol{m}_{\boldsymbol{x}}^{\mathrm{T}} Cx=M1k=1∑MxkxkT−mxmxT
或者根据协方差矩阵定义来求
②计算该协方差矩阵的特征值和特征向量;
③将特征向量按照它们对应的特征值大小进行排序;
④挑选出与较大特征值对应的重要特征向量;
⑤将原始信号投影到所选特征向量构成的空间上,从而得到一个低维信号。
基本步骤:
(1) 选3个以上点的坐标构成一组矢量 x x x
(2)计算x的均值矢量m_和协方差矩阵 C x C_{x} Cx
(3)计算 C x C_{x} Cx 的特征值,获得特征矢量矩阵A(A的第一列对应最大特征值的特征向量,向下递减)
(4)霍特林变换:用A乘以原始矢量和均值 矢量的差
y = A ( x − m x ) y=A\left(x-m_{x}\right) y=A(x−mx)
y : \boldsymbol{y}: y: 均值为零
m y = 0 m_{y}=0 my=0
(5)近似重建:从y重建x
近似重建 :
x ^ = A K T y + m x \hat{x}=A_{K}^{\mathrm{T}} y+m_{x} x^=AKTy+mx
均方误差 :
e m s = ∑ j = 1 N λ j − ∑ j = 1 K λ j = ∑ j = K + 1 N λ j ( λ j 是 递 减 的 ) e_{\mathrm{ms}}=\sum_{j=1}^{N} \lambda_{j}-\sum_{j=1}^{K} \lambda_{j}=\sum_{j=K+1}^{N} \lambda_{j}(\lambda_{j}是递减的) ems=j=1∑Nλj−j=1∑Kλj=j=K+1∑Nλj(λj是递减的)
方程含义计算没选中的特征值的和
CV10-纹理
目标检测时,首先要选用合适的特征描述,将纹理区域和平滑区域分割开以便自适应的选取局部最优特征做进一步识别
与纹理有关的任务
从纹理中获取形状–根据图像纹理估计表面方向或形状
使用点到点的纹理变形来估计表面形状
classification ,指所考查的是 整幅图像的纹理,目标是对该幅纹理图像进行分类,判断每幅图像所属的纹理类别;分类前,要有一些关于纹理图像的先验知识。
Segmentation ,研究对象是包含多种纹理类别的图像,它将纹理图像划分成若干区域,这些区域分别具有相对一致的纹理描述且互不相交。——这是纹理分析中一个较难问题,因为通常事先并不知道图像中存在哪些纹理,多少纹理,以及哪些区域包含哪类纹理。 分割的关键:如何区分两种纹理,即根据什么标准来确定两种纹理的不同
灰度共生矩阵###
一幅图像的灰度级数一般是256 ,这样计算的灰度共生矩阵太大,在求灰度共生矩阵之前,常压缩为16 级
根据像素值表,再根据要求的点对(规定形状)找出要找的灰度值点对,计算该灰度值点对出现的次数
共生矩阵是要次数除以总次数的概率
位置算子
注意位置算子的坐标(1,1)代表-45° 和a,b表示的不一样
(0,1)代表-90°
基于共生矩阵的描述###
各种描述量
想ppt那俩图,一个墙壁,一堆豆子
- 二阶矩(能量):
含义:是灰度共生矩阵各元素值的平方和,反应了图像灰度分布均匀程度和纹理粗细度
性质:如果共生矩阵的所有值均相等,则能量值小;相反,如果其中一些值大而其他值小,则能量值大。当共生矩阵中元素集中分布时,能量值大。 能量值大表明一种较均一和规则变化的纹理模式。(如果图像平缓区域多或者纹理都差不多,那某些值会很大) - 熵:
W E = − ∑ g 1 ∑ g 2 p ( g 1 , g 2 ) log p ( g 1 , g 2 ) W_{\mathrm{E}}=-\sum_{g_{1}} \sum_{g_{2}} p\left(g_{1}, g_{2}\right) \log p\left(g_{1}, g_{2}\right) WE=−g1∑g2∑p(g1,g2)logp(g1,g2)
含义:描述图像具有的信息量的度量,纹理信息也属于图像信息,给出了图像内容随机性的量度。
性质:当图像无纹理时,熵=0;满纹理时,熵最大。从数学角度看,当矩阵中所有元素近似相等时熵应该最大。 它表示了图像中 纹理的非 均匀程度或复杂程度。当复杂程度高时,熵值较大,反之则较小
3.对比度:
W C = ∑ g 1 ∑ g 2 ∣ g 1 − g 2 ∣ p ( g 1 , g 2 ) W_{\mathrm{C}}=\sum_{g_{1}} \sum_{g_{2}}\left|g_{1}-g_{2}\right| p\left(g_{1}, g_{2}\right) WC=g1∑g2∑∣g1−g2∣p(g1,g2)
含义: 反映了图像的清晰程度和纹理沟纹深浅的程度。
性质:纹理沟纹越深,其对比度越大,视觉效果越清晰; 反之,对 比度小,则沟纹浅,效果模糊。如果对比度大的像素对越多,这个 值就越大。灰度共生矩阵中远离对角线的元素值越大(g1-g2),对比度越大。
4.均匀性:
W H = ∑ g 1 ∑ g 2 p ( g 1 , g 2 ) k + ∣ g 1 − g 2 ∣ ∣ W_{\mathrm{H}}=\sum_{g_{1}} \sum_{g_{2}} \frac{p\left(g_{1}, g_{2}\right)}{k+\left|g_{1}-g_{2}\right|} \mid WH=g1∑g2∑k+∣g1−g2∣p(g1,g2)∣
含义:反映图像纹理的同质性,度量图像纹理局部变化的多少。
性质:其值大则说明图像纹理的不同区域间缺少变化,局部非常均匀。
应用
基于能量的描述###
只依靠单个像素及其邻域的灰度分布或某种属性去作纹理测量,其方法就称为一阶统计分析法。
利用**模板(也称核)**计算局部纹理能量可以获得灰度变化的信息
f ( x , y ) → 微窗口滤波 → F ( x , y ) → 能量转换 → E ( x , y ) → 分类 \mathrm{f}(\mathrm{x}, \mathrm{y}) \rightarrow \text { 微窗口滤波 } \rightarrow \mathrm{F}(\mathrm{x}, \mathrm{y}) \rightarrow \text { 能量转换 } \rightarrow \mathrm{E}(\mathrm{x}, \mathrm{y}) \rightarrow \text { 分类 } f(x,y)→ 微窗口滤波 →F(x,y)→ 能量转换 →E(x,y)→ 分类
微窗口滤波:用好几个模板作用原始图像,每个模板都得到一个结果图
能量转换:分别对n个模板得到的n个结果图做纹理能量图转换
E n ( r , c ) = ∑ i = c − 2 c + 2 ∑ j = r − 2 r + 2 ∣ F n ( i , j ) ∣ 其中,c和r分别代表行和列 \begin{aligned} &E_{n}(r, c)=\sum_{i=c-2}^{c+2} \sum_{j=r-2}^{r+2}\left|F_{n}(i, j)\right|\\ &\text { 其中,c和r分别代表行和列 } \end{aligned} En(r,c)=i=c−2∑c+2j=r−2∑r+2∣Fn(i,j)∣ 其中,c和r分别代表行和列 每幅纹理能量图像都是完全尺寸的图像,代表用第n个模板得
到的结果。
双目视觉
三个坐标系
图像坐标系有俩
图像坐标为二维坐标,分为两种: ( u , v ) 是以像素为单位的图像坐标 ( x , y ) 是以毫米为单位的图像坐标 \begin{array}{c} \text { 图像坐标为二维坐标,分为两种: } \\ (u, \quad v) \text { 是以像素为单位的图像坐标 } \\ (x, \quad y) \text { 是以毫米为单位的图像坐标 } \end{array} 图像坐标为二维坐标,分为两种: (u,v) 是以像素为单位的图像坐标 (x,y) 是以毫米为单位的图像坐标
基本原理
根据摄像机成像原理,空间一点 P ( x w , y w , z w ) P\left(x_{w}, y_{w}, z_{w}\right) P(xw,yw,zw) 在图像中的像点 p ( u , v ) p(u, v) p(u,v) 是 P P P 点 与摄像机光心O的连线与摄像机屏幕的交点。若已知空间一点P在左、右摄像 机图像中的像点分别为 p 1 ( u 1 , v 1 ) p_{1}\left(u_{1}, v_{1}\right) p1(u1,v1) 与 p 2 ( u 2 , v 2 ) , p_{2}\left(u_{2}, v_{2}\right), p2(u2,v2), 则原空间点P位于空间射线 o 1 p 1 o_{1} p_{1} o1p1 与 o 2 p 2 o_{2} p_{2} o2p2 的延长线交点上 ( o 1 , o 2 \left(o_{1}, o_{2}\right. (o1,o2 分别为左右摄像机的光心 ) , ), ), 对空间射线 o 1 p 1 o_{1} p_{1} o1p1 与 o 2 p 2 o_{2} p_{2} o2p2 求交即可反求出点P的三维坐标。双目视觉可以看作是由图像坐标向三 维世界坐标映射的一个过程。
双目视觉的关键之一是:给定 p 1 ( u 1 , v 1 ) , 求出对应的 p 2 ( u 2 , v 2 ) ∘ \begin{aligned} &\text { 双目视觉的关键之一是:给定 }\\ &p_{1}\left(u_{1}, v_{1}\right), \text { 求出对应的 } p_{2}\left(u_{2}, v_{2}\right)_{\circ} \end{aligned} 双目视觉的关键之一是:给定 p1(u1,v1), 求出对应的 p2(u2,v2)∘
这里的 p 1 ( u 1 , v 1 ) p_{1}\left(u_{1}, v_{1}\right) p1(u1,v1) 的 u 1 , v 1 u_{1}, v_{1} u1,v1指的都是像素的坐标,坐标原点在图像的最左上方
具体实现
1.摄像机定标
目标:求摄像机成像变换矩阵
此处省略一万条公式
-
图像坐标的转换(u,v)到(x,y)
-
世界坐标到摄像机坐标转换。摄像机坐标系和世界坐标系之间的关系可以用一旋转矩阵R和一平移向量t描述
-
摄像机坐标到像素坐标的变换
-
最终得到世界坐标系中的点 P ( X w , y w , Z w ) P\left(X_{w}, \quad y_{w}, \quad Z_{w}\right) P(Xw,yw,Zw)在摄像机屏幕上对应的图像 p ( u , v ) 计算公式 p(u, \quad v) \text { 计算公式 } p(u,v) 计算公式
2.立体匹配
两个对应的像素点有大致相同的特征,两个像素点与立体点在一个平面上,在平面与图像坐标交线上进行搜寻。