NNDL 实验二 pytorch入门

一、概念：张量、算子

算子：

算子是一个函数空间到函数空间上的映射  0: X→X   广义上的算子可以推广到任何空间，如内积空间等。深度学习算法由一个个计算单元组成，我们称这些计算单元为算子。在网络模型中，算子对应层中的计算逻辑，比如卷积层是一个算子，全连接层中的权值求和过程也称之是一个算子
广义的讲，对任何函数进行某一项操作都可以认为是一个算子，算子就是映射，就是关系，就是变换。从一个函数空间(比如Banach空间、 Hilbert空间、 Sobolev空间) 到另一个函数空间。注意，函数空间当然属于拓扑空间，而且是拓扑线性空间，不过是无限维度的。而无限维的拓扑“非线性”空间一般称为Banach流形/Hilbert流形。因此算子属于映射。
有的时候，从有限维空间到有限维空间的映射也会称为“算子”，比如矩阵，是最常见的线性算子。
 

张量：

张量是算子计算数据的容器，包括输入数据与输出数据

张量是一种表示物理量的方式，这个方式就是用基向量与分量组合表示物理量

1.张量是多维数组，这个定义常见于各种人工智能软件。
2.张量是某种几何对象，不会随着坐标系的改变而改变
3.张量是向量和余向量（covector）通过张量积（tensor product）组合而成的。
4.张量是多重线性映射

由于基向量可以有丰富的组合，张量可以表示非常丰富的物理量。此外，张量所描述的物理量是不随观察者或者说参照系而变化的，当参照系变化时（其实就是基向量变化），其分量也会相应变化，最后结果就是基向量与分量的组合（也就是张量）保持不变。这一点对于我们构造数据对象，进而展开分析建模，有着至关重要的意义

过去我们对“量”的认识过程，我们都懂得用“一个数”来表示数量（标量），用“一个数组”（列矩阵或行矩阵）来表示一个向量，这都属于代数手法。如果采用几何手法，标量中的实数可以表示为一维坐标系（如数轴）上的一个点，复数可以表示为二维坐标系（如复平面）上的一个点。向量通常可以表示为二维、三维或更高维坐标系中的一个空间点或有向线段。如果我们把代数手法和几何手法结合起来即采用解析几何的手法，向量又可以表示为某种坐标基向量和坐标分量的线性组合。

张量的数据结构形象有一阶张量 二阶张量 ......M阶张量。一阶张量可以理解为一个向量，二阶张量可以理解为矩阵，三阶张量可以理解成立方体，四阶张量可以理解成立方体组成的一个向量，五阶张量可以理解成立方体组成的矩阵，依次类推。计算机很擅长做这类数据结构的运算和处理，所以我们研究和普及张量算法

在深度学习的实践中，我们通常使用向量或矩阵运算来提高计算效率。比如​w1​x1​+w2​x2​+⋯+wN​xN的计算可以用w⊤x来代替，（其中w=[w1w2⋯wN]⊤，x=[x1​x2​⋯xN​]⊤），这样可以充分利用计算机的并行计算能力，特别是利用GPU来实现高效矩阵运算。

在深度学习框架中，数据经常用张量(Tensor)的形式来存储。张量是矩阵的扩展与延伸，可以认为是高阶的矩阵。1阶张量为向量，2阶张量为矩阵。如果你对Numpy熟悉，那么张量是类似于Numpy的多维数组(ndarray)的概念，可以具有任意多的维度。

注：这里的“维度”是“阶”的概念，和线性代数中向量的“维度”含义不同。

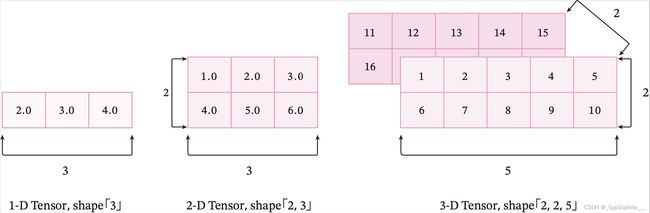
张量的大小可以用形状（shape）来描述。比如一个三维张量的形状是 [2,2,5][2, 2, 5][2,2,5]，表示每一维（也称为轴（axis））的元素的数量，即第0轴上元素数量是2，第1轴上元素数量是2，第2轴上的元素数量为5。

图1.5给出了3种纬度的张量可视化表示。

 张量中元素的类型可以是布尔型数据、整数、浮点数或者复数，但同一张量中所有元素的数据类型均相同。因此我们可以给张量定义一个数据类型(dtype)来表示其元素的类型。

二、使用pytorch实现张量运算

1.2 张量

1.2.1 创建张量
1.2.1.1 指定数据创建张量

（1）通过指定的Python列表数据[2.0, 3.0, 4.0]，创建一个一维张量。

# 导入torch
import torch
# 创建一维Tensor
data = torch.Tensor([2.0,3.0,4.0])
print(data)

tensor([2., 3., 4.])

（2）通过指定的Python列表数据来创建类似矩阵（matrix）的二维张量。

# 创建二维Tensor
import torch
data = torch.Tensor([[1.0, 2.0, 3.0] ，[4.0, 5.0, 6.0]])
print(data)

tensor([[1., 2., 3.],
        [4., 5., 6.]])

（3）同样地，还可以创建维度为3、4...N等更复杂的多维张量。

# 创建多维Tensor
import torch
data = torch.Tensor([[[1, 2, 3, 4, 5],
                      [6, 7, 8, 9, 10]],
                     [[11, 12, 13, 14, 15],
                      [16, 17, 18, 19, 20]]])
print(data)

 tensor([[[ 1.,  2.,  3.,  4.,  5.],
         [ 6.,  7.,  8.,  9., 10.]],
 
        [[11., 12., 13., 14., 15.],
        [16., 17., 18., 19., 20.]]])

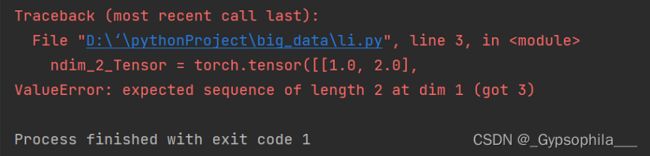
需要注意的是，张量在任何一个维度上的元素数量必须相等。下面尝试定义一个在同一维度上元素数量不等的张量。

# 尝试定义在不同维度上元素数量不等的Tensor
ndim_2_Tensor = torch.tensor([[1.0, 2.0],
                                  [4.0, 5.0, 6.0]])

 

 注：从输出结果看，这种定义情况会抛出异常，提示在任何维度上的元素数量必须相等。

1.2.1.2 指定形状创建

如果要创建一个指定形状、元素数据相同的张量，可以使用paddle.zeros、paddle.ones、paddle.full等API。

m, n = 2, 3
# 创建数据全为0，形状为[m, n]的Tensor
zeros_Tensor = torch.zeros([m, n])
# 创建数据全为1，形状为[m, n]的Tensor
ones_Tensor = torch.ones([m, n])
# 创建数据全为指定值，形状为[m, n]的Tensor，这里我们指定数据为8
full_Tensor = torch.full([m, n], 10)
print('zeros Tensor: ', zeros_Tensor)
print('ones Tensor: ', ones_Tensor)
print('full Tensor: ', full_Tensor)

zeros Tensor:  tensor([[0., 0., 0.],
        [0., 0., 0.]])
ones Tensor:  tensor([[1., 1., 1.],
        [1., 1., 1.]])
full Tensor:  tensor([[10, 10, 10],
        [10, 10, 10]])

1.2.1.3 指定区间创建

如果要在指定区间内创建张量，可以使用paddle.arange、paddle.linspace等API。

import torch
# 创建以步长step=2均匀分隔数值区间[start=1, end=6)的一维Tensor
arange_Tensor = torch.arange(1, 6, 2)
# 创建以元素个数num=5均匀分隔数值区间[start=1, stop=5]的Tensor
linspace_Tensor = torch.linspace(1, 5, 5)
print('arange Tensor: ', arange_Tensor)
print('linspace Tensor: ', linspace_Tensor)

arange Tensor:  tensor([1, 3, 5])
linspace Tensor:  tensor([1., 2., 3., 4., 5.])

1.2.2 张量的属性
1.2.2.1 张量的形状

• Tensor.ndim：张量的维度，例如向量的维度为1，矩阵的维度为2。
• Tensor.shape： 张量每个维度上元素的数量。
• Tensor.shape[n]：张量第nnn维的大小。第nnn维也称为轴（axis）。
• Tensor.size：张量中全部元素的个数。

创建一个四维张量，并打印出shape、ndim、shape[n]、size属性。

import torch
ndim_4_Tensor = torch.tensor([2, 3, 4, 5])
print("Number of dimensions:", ndim_4_Tensor.ndim)
print("Shape of Tensor:", ndim_4_Tensor.shape)
print("Elements number along axis 0 of Tensor:", ndim_4_Tensor.shape[0])
print("Elements number along the last axis of Tensor:", ndim_4_Tensor.shape[-1])
print('Number of elements in Tensor: ', ndim_4_Tensor.size())

Number of dimensions: 1
Shape of Tensor: torch.Size([4])
Elements number along axis 0 of Tensor: 4
Elements number along the last axis of Tensor: 4
Number of elements in Tensor:  torch.Size([4])

1.2.2.2 形状的改变

除了查看张量的形状外，重新设置张量的在实际编程中也具有重要意义，飞桨提供了paddle.reshape接口来改变张量的形状。

import torch
# 定义一个shape为[3,2,5]的三维Tensor
ndim_3_Tensor = torch.tensor([[[1, 2, 3, 4, 5],
                                   [6, 7, 8, 9, 10]],
                                  [[11, 12, 13, 14, 15],
                                   [16, 17, 18, 19, 20]],
                                  [[21, 22, 23, 24, 25],
                                   [26, 27, 28, 29, 30]]])
print("the shape of ndim_3_Tensor:", ndim_3_Tensor.shape)
# paddle.reshape 可以保持在输入数据不变的情况下，改变数据形状。这里我们设置reshape为[2,5,3]
reshape_Tensor = torch.reshape(ndim_3_Tensor, [2, 5, 3])
print("After reshape:", reshape_Tensor)

the shape of ndim_3_Tensor: torch.Size([3, 2, 5])
After reshape: tensor([[[ 1,  2,  3],
         [ 4,  5,  6],
         [ 7,  8,  9],
         [10, 11, 12],
         [13, 14, 15]],

        [[16, 17, 18],
         [19, 20, 21],
         [22, 23, 24],
         [25, 26, 27],
         [28, 29, 30]]])

注：张量形状改变，但内部数据不会发生变化，元素顺序也不变，只是数据形状发生改变 

1.2.2.3 张量的数据类型

import torch
print("Tensor dtype from Python integers:", torch.tensor(1).dtype)
print("Tensor dtype from Python floating point:", torch.tensor(1.0).dtype)

Tensor dtype from Python integers: torch.int64
Tensor dtype from Python floating point: torch.float32```

1.2.2.4 张量的设备位置

import torch
ndim_4_Tensor = torch.tensor([2, 3, 4, 5])
print(ndim_4_Tensor.device

cpu

1.2.3 张量与Numpy数组转换

张量和Numpy数组可以相互转换。第1.2.2.3节中我们了解到paddle.to_tensor()函数可以将Numpy数组转化为张量，也可以通过Tensor.numpy()函数将张量转化为Numpy数组

import torch
ndim_1_Tensor = torch.tensor([1., 2.])
# 将当前 Tensor 转化为 numpy.ndarray
print('Tensor to convert: ', ndim_1_Tensor.numpy())

Tensor to convert:  [1. 2.]

1.2.4 张量的访问
1.2.4.1 索引和切片

索引：

import torch
data = torch.Tensor([[1.0, 2.0, 3.0],
                                  [4.0, 5.0, 6.0]])
print(data[1])

tensor([4., 5., 6.])

切片

print(data[0:1])

tensor([[1., 2., 3.]])

1.2.4.2 访问张量

print(data[0:2, 1:3])

tensor([[2., 3.],
        [5., 6.]])

1.2.4.3 修改张量

tensor([[2., 3.],
        [5., 6.]])

tensor([[1., 2., 3.],
        [7., 5., 6.]])

注： 慎重通过索引或切片操作来修改张量，此操作仅会原地修改该张量的数值，且原值不会被保存。如果被修改的张量参与梯度计算，将仅会使用修改后的数值，这可能会给梯度计算引入风险。

1.2.5 张量的运算

由于张量类成员函数操作更为方便，以下均从张量类成员函数的角度，对常用张量操作进行介绍。

1.2.5.1 数学运算

import torch
x = torch.tensor([[1., 2.], [3., 4.]])
y = torch.tensor([[5., 6.], [7., 8.]])
print("加法运算：",x + y)
print("减法运算：",x - y)
print("乘法运算：",x * y)
print("除法运算：",x / y)
print("幂运算：",x**y)
print("对数运算：",torch.log(x))
print("开方运算：",torch.sqrt(y)

加法运算： tensor([[ 6.,  8.],
        [10., 12.]])
减法运算： tensor([[-4., -4.],
        [-4., -4.]])
乘法运算： tensor([[ 5., 12.],
        [21., 32.]])
除法运算： tensor([[0.2000, 0.3333],
        [0.4286, 0.5000]])
幂运算： tensor([[1.0000e+00, 6.4000e+01],
        [2.1870e+03, 6.5536e+04]])
对数运算： tensor([[0.0000, 0.6931],
        [1.0986, 1.3863]])
开方运算： tensor([[2.2361, 2.4495],
        [2.6458, 2.8284]])

1.2.5.2 逻辑运算

import torch
x= torch.tensor([[True, True], [True, True]])
y= torch.tensor([[False, False], [False, False]])
print(x & y)    # 与运算
print(x | y)    # 或运算
print(~x)   # 取反
print(x ^ y)    # 异或运算
print(torch.eq(x, y))    # 判断每个分量是否相等
print(torch.equal(x, y))     # 判断整体是否相等

tensor([[False, False],
        [False, False]])
tensor([[True, True],
        [True, True]])
tensor([[False, False],
        [False, False]])
tensor([[True, True],
        [True, True]])
tensor([[False, False],
        [False, False]])
False

Process finished with exit code -1073741749 (0xC000004B)

1.2.5.3 矩阵运算

乘法

import torch
x = torch.arange(12, dtype=torch.float32).reshape((4, 3))
y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print("矩阵相乘：", x.matmul(y) )

矩阵相乘： tensor([[ 9.,  8.,  7.,  6.],
        [30., 26., 34., 30.],
        [51., 44., 61., 54.],
        [72., 62., 88., 78.]])

转置

import torch
x = torch.ones(2, 1)
print(x)
print("转置后：",x.t())

tensor([[1.],
        [1.]])
转置后： tensor([[1., 1.]])

1.2.5.4 广播机制

飞桨的一些API在计算时支持广播(Broadcasting)机制，允许在一些运算时使用不同形状的张量。通常来讲，如果有一个形状较小和一个形状较大的张量，会希望多次使用较小的张量来对较大的张量执行某些操作，看起来像是形状较小的张量首先被扩展到和较大的张量形状一致，然后再做运算。

广播机制的条件

飞桨的广播机制主要遵循如下规则（参考Numpy广播机制）：

1）每个张量至少为一维张量。

2）从后往前比较张量的形状，当前维度的大小要么相等，要么其中一个等于1，要么其中一个不存在。

import torch
# 当两个Tensor的形状一致时，可以广播
x = torch.ones((2, 3, 4))
y = torch.ones((2, 3, 4))
z = x + y
print('broadcasting with two same shape tensor: ', z.shape)
x = torch.ones((2, 3, 1, 5))
y = torch.ones((3, 4, 1))
# 从后往前依次比较：
# 第一次：y的维度大小是1
# 第二次：x的维度大小是1
# 第三次：x和y的维度大小相等，都为3
# 第四次：y的维度不存在
# 所以x和y是可以广播的
z = x + y
print('broadcasting with two different shape tensor:', z.shape)

broadcasting with two same shape tensor:  torch.Size([2, 3, 4])
broadcasting with two different shape tensor: torch.Size([2, 3, 4, 5])

广播机制的计算规则

现在我们知道在什么情况下两个张量是可以广播的。两个张量进行广播后的结果张量的形状计算规则如下：

1）如果两个张量shape的长度不一致，那么需要在较小长度的shape前添加1，直到两个张量的形状长度相等。

2） 保证两个张量形状相等之后，每个维度上的结果维度就是当前维度上较大的那个。

三. 数据预处理

1. 读取数据集 house_tiny.csv、boston_house_prices.csv、Iris.csv

import pandas as pd
house_tiny_path = './house_tiny.csv'
boston_house_prices_path = './boston_house_prices.csv'
Iris_path = './Iris.csv'
house_tiny_data = pd.read_csv(house_tiny_path)
boston_house_prices_data = pd.read_csv(boston_house_prices_path)
Iris_data = pd.read_csv(Iris_path)
print(house_tiny_data)
print(boston_house_prices_data)
print(boston_house_prices_data)

   NumRooms Alley   Price
0       NaN  Pave  127500
1       2.0   NaN  106000
2       4.0   NaN  178100
3       NaN   NaN  140000
        CRIM    ZN  INDUS  CHAS    NOX  ...  RAD  TAX  PTRATIO  LSTAT  MEDV
0    0.00632  18.0   2.31     0  0.538  ...    1  296     15.3   4.98  24.0
1    0.02731   0.0   7.07     0  0.469  ...    2  242     17.8   9.14  21.6
2    0.02729   0.0   7.07     0  0.469  ...    2  242     17.8   4.03  34.7
3    0.03237   0.0   2.18     0  0.458  ...    3  222     18.7   2.94  33.4
4    0.06905   0.0   2.18     0  0.458  ...    3  222     18.7   5.33  36.2
..       ...   ...    ...   ...    ...  ...  ...  ...      ...    ...   ...
501  0.06263   0.0  11.93     0  0.573  ...    1  273     21.0   9.67  22.4
502  0.04527   0.0  11.93     0  0.573  ...    1  273     21.0   9.08  20.6
503  0.06076   0.0  11.93     0  0.573  ...    1  273     21.0   5.64  23.9
504  0.10959   0.0  11.93     0  0.573  ...    1  273     21.0   6.48  22.0
505  0.04741   0.0  11.93     0  0.573  ...    1  273     21.0   7.88  11.9

[506 rows x 13 columns]
        CRIM    ZN  INDUS  CHAS    NOX  ...  RAD  TAX  PTRATIO  LSTAT  MEDV
0    0.00632  18.0   2.31     0  0.538  ...    1  296     15.3   4.98  24.0
1    0.02731   0.0   7.07     0  0.469  ...    2  242     17.8   9.14  21.6
2    0.02729   0.0   7.07     0  0.469  ...    2  242     17.8   4.03  34.7
3    0.03237   0.0   2.18     0  0.458  ...    3  222     18.7   2.94  33.4
4    0.06905   0.0   2.18     0  0.458  ...    3  222     18.7   5.33  36.2
..       ...   ...    ...   ...    ...  ...  ...  ...      ...    ...   ...
501  0.06263   0.0  11.93     0  0.573  ...    1  273     21.0   9.67  22.4
502  0.04527   0.0  11.93     0  0.573  ...    1  273     21.0   9.08  20.6
503  0.06076   0.0  11.93     0  0.573  ...    1  273     21.0   5.64  23.9
504  0.10959   0.0  11.93     0  0.573  ...    1  273     21.0   6.48  22.0
505  0.04741   0.0  11.93     0  0.573  ...    1  273     21.0   7.88  11.9

[506 rows x 13 columns]

Process finished with exit code -1073741749 (0xC000004B)

2. 处理缺失值

import pandas as pd
house_tiny_path = './house_tiny.csv'
boston_house_prices_path = './boston_house_prices.csv'
Iris_path = './Iris.csv'
house_tiny_data = pd.read_csv(house_tiny_path)
boston_house_prices_data = pd.read_csv(boston_house_prices_path)
Iris_data = pd.read_csv(Iris_path)
X = house_tiny_data.iloc[:, 0:2]
print(X)
y = house_tiny_data.iloc[:, 2]
print(y)
X = X.fillna(X.mean())
print(X)

NumRooms Alley
0       NaN  Pave
1       2.0   NaN
2       4.0   NaN
3       NaN   NaN
0    127500
1    106000
2    178100
3    140000
Name: Price, dtype: int64
   NumRooms Alley
0       3.0  Pave
1       2.0   NaN
2       4.0   NaN
3       3.0   NaN

3. 转换为张量格式
 

import pandas as pd
import torch
import numpy as np
house_tiny_path = './house_tiny.csv'
boston_house_prices_path = './boston_house_prices.csv'
Iris_path = './Iris.csv'
house_tiny_data = pd.read_csv(house_tiny_path)
boston_house_prices_data = pd.read_csv(boston_house_prices_path)
Iris_data = pd.read_csv(Iris_path)
X = house_tiny_data.iloc[:, 0:2]
y = house_tiny_data.iloc[:, 2]
X = pd.get_dummies(X, dummy_na=True)
X_tensor, y_tensor = torch.Tensor(X.values), torch.Tensor(y.values)
print(X_tensor, y_tensor)

tensor([[nan, 1., 0.],
        [2., 0., 1.],
        [4., 0., 1.],
        [nan, 0., 1.]]) tensor([127500., 106000., 178100., 140000.])

实验心得体会：首先通过对张量和算子概念的理解，可以对后面的张量的运算打下基础，更好的理解实验过程，掌握了通过pytorch实现张量的运算，学会创建访问张量，对张量进行一些数学运算、逻辑运算、矩阵运算以及广播体制。还学会了使用pytorch实现数据的预处理。