深入理解NLP中LayerNorm的原理以及LN的代码详解

深入理解NLP中LayerNorm的原理以及LN的代码详解

在介绍LayerNorm之前，我们先来思考一下，为什么NLP中要引入LayerNorm？

如果你学过一点深度学习，那么应该多多少少听过BatchNorm这个东西。BN简单来说就是对一批样本按照每个特征维度进行归一化。BN具体细节请看我的另一篇博客：深入理解BatchNorm的原理

以下图为例演示下BatchNorm的过程，我们会对R个样本的“成绩”这个特征维度做归一化。

但在NLP领域，每个样本通常是一个句子，而句子中包含若干个单词。这时如果使用BN去做过归一化通常效果会很差。

那有没有更好的归一化方法呢？

有的，我们今天就来看一看NLP中常用的归一化操作：LayerNorm

LayerNorm原理

在NLP中，大多数情况下大家都是用LN（LayerNorm）而不是BN（BatchNorm）。最直接的原因是BN在NLP中效果很差，所以一般不用。

论文题目：Layer Normalization
论文链接：https://arxiv.org/abs/1607.06450

官方文档：torch.nn.LayerNorm
torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, device=None, dtype=None)

• Input: $(N,\ast )$
• Output: $(N,\ast )$(same shape as input)

LayerNorm中没有batch的概念，所以不会像BatchNorm那样跟踪统计全局的均值方差，因此train()和eval()对LayerNorm没有影响。

说明：nn.LayerNorm与nn.BatchNorm用法上有很大的差异

• nn.BatchNorm2d(num_features)中的num_features一般是输入数据的第2维(从1开始数），BatchNorm中weight和bias与num_features一致。

• nn.LayerNorm(normalized_shape)中的normalized_shape是最后的几维，LayerNorm中weight和bias的shape就是传入的normalized_shape。

在取平均值和方差的时候两者也有差异：

• BN是把除了轴num_features外的所有轴的元素放在一起，取平均值和方差的，然后对每个元素进行归一化，最后再乘以对应的$\gamma$和$\beta$（共享）。BN共有num_features个mean和var，（假设输入数据的维度为(N,num_features, H, W））。
• 而LN是把normalized_shape这几个轴的元素都放在一起，取平均值和方差的，然后对每个元素进行归一化，最后再乘以对应的$\gamma$和$\beta$（每个元素不同）。LN共有N1*N2个mean和var（假设输入数据的维度为(N1,N2,normalized_shape），normalized_shape表示多个维度）
  

示例1：NLP中的LayerNorm（常用）

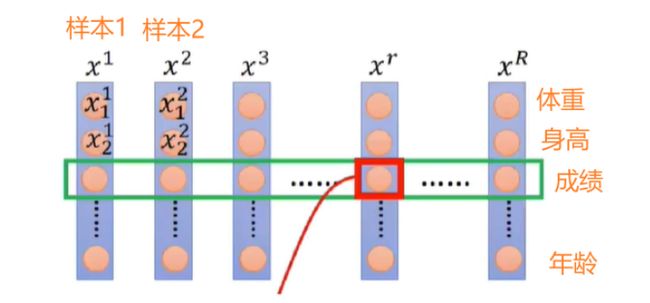
NLP的输入一般是(batch, sentence_length, embedding_dim)，则LayerNorm层有embedding_dim个参数$\gamma$和$\beta$。也就是对于输入的单词序列，LN是对一个单词的embedding向量进行归一化的

import torch
import torch.nn as nn

# ===== NLP Example =====
batch, sentence_length, embedding_dim = 20, 5, 10
inputs = torch.randn(batch, sentence_length, embedding_dim)
layer_norm = nn.LayerNorm(embedding_dim)

print("LayerNorm只有参数gamma和beta，没有统计量")
print(layer_norm.state_dict().keys())
print("参数gamma shape: ", layer_norm.state_dict()['weight'].shape)
print("参数beta shape: ", layer_norm.state_dict()['bias'].shape)
print("输入：", inputs.shape)
print("输出：", layer_norm(inputs).shape)

输出：

LayerNorm只有参数gamma和beta，没有统计量
odict_keys(['weight', 'bias'])
参数gamma shape:  torch.Size([10])
参数beta shape:  torch.Size([10])
输入： torch.Size([20, 5, 10])
输出： torch.Size([20, 5, 10])

图解：Layer Norm到底是怎么对单词归一化的？

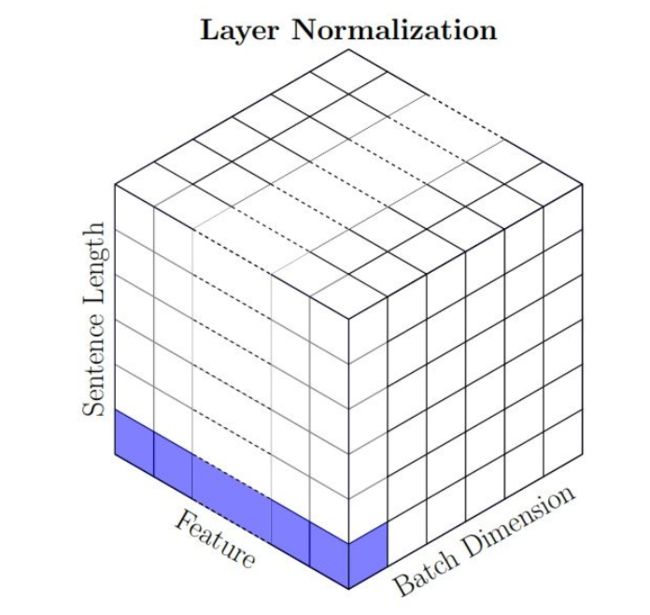
（有错误）下图Layer Normalization计算过程（来自猛猿），乍一看好像是在描述LayerNorm，但是对应到NLP中的数据，就不太正确了，所以建议结合我上面的图去理解。

思考题1：为什么Layer Norm是对每个单词的Embedding做归一化？

看到这，可能很多人会有疑问了，为什么Layer Norm是对每个单词的embedding进行归一化，而不是对这个序列的所有单词embedding向量的相同维度进行归一化呢？

我一开始也是觉得应该对所有单词embedding向量归一化，但后来发现pytorch官方实现的LayerNorm并不是这样实现的，而是对每个单词的embedding进行了归一化。

后来，我想明白了，因为每个序列（每个样本）的单词个数不一样，但在代码实现的时候会进行padding，比如一个序列原始单词数为30个，另一个序列原始单词数是8，然后你统一padding成了30个单词，那如果按照相同维度，进行归一化，norm的信息就会被无意义的padding的embedding冲淡的！这显然是不合理的。

思考题2：为什么BN训练和测试时有区别，而LN没区别？

BatchNorm的统计量是一个batch算出来的，在线测试时，不太可能累计一个batch资料后再进行测试的。所以在训练的时候要记录统计量running mean和running var，作为预测时的均值和方差。详见博客：深入理解BatchNorm的原理

而LayerNorm训练和测试的时候不需要model.train()和model.eval()，是因为它只针对一个样本，不是针对一个batch，所以LayerNorm只有参数gamma和beta，没有统计量，因此LN训练和预测没有区别。

Transformer模型中的LayerNorm

# 这里选取了Transformer模型的部分代码
class PoswiseFeedForwardNet(nn.Module):
    def __init__(self):
        super(PoswiseFeedForwardNet, self).__init__()
        self.fc = nn.Sequential(
            nn.Linear(d_model, d_ff, bias=False),
            nn.ReLU(),
            nn.Linear(d_ff, d_model, bias=False)
        )

    def forward(self, inputs):
        """
        inputs: [batch_size, seq_len, d_model]
        """
        # inputs shape: [batch_size, seq_len, d_model]
        residual = inputs
        output = self.fc(inputs)
        # output shape: [batch_size, seq_len, d_model]
        return nn.LayerNorm(d_model).to(device)(output + residual)

示例2：CV中LayerNorm的应用（不常用）

import torch
import torch.nn as nn


print("===== Image Example =====")
N, C, H, W = 20, 5, 10, 10
inputs = torch.randn(N, C, H, W)
# Normalize over the last three dimensions (i.e. the channel and spatial dimensions)
# as shown in the image below
layer_norm = nn.LayerNorm([C, H, W])
print("LayerNorm只有参数gamma和beta，没有统计量")
print(layer_norm.state_dict().keys())
print("参数gamma shape: ", layer_norm.state_dict()['weight'].shape)
print("参数beta shape: ", layer_norm.state_dict()['bias'].shape)
print("输入：", inputs.shape)
print("输出：", layer_norm(inputs).shape)

输出：

===== Image Example =====
LayerNorm只有参数gamma和beta，没有统计量
odict_keys(['weight', 'bias'])
参数gamma shape:  torch.Size([5, 10, 10])
参数beta shape:  torch.Size([5, 10, 10])
输入： torch.Size([20, 5, 10, 10])
输出： torch.Size([20, 5, 10, 10])

下面这个图C表示通道数，H,W表示高和宽，由于可视化的原因，下图把H,W放在一起了，实际上像下图橙色形状是一个特征图（某个通道下的H*W）

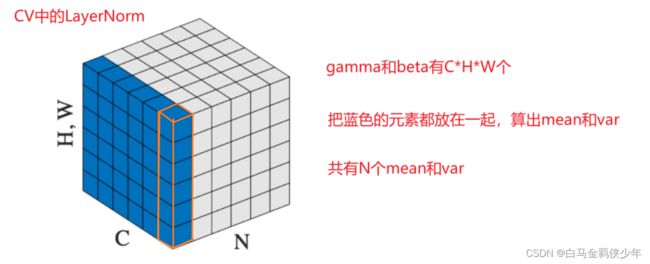
显然LN求mean和var的时候是把整个蓝色元素都放在一起求的，然后每个元素都用这个mean和var进行归一化，不过这里每个元素对应的$\gamma$和$\beta$是不同的，因为$\gamma$和$\beta$也有$C\ast H\ast W$个。

附：BN、LN、IN、GN的区别

神经网络中有很多归一化的算法：Batch Normalization (BN)、Layer Normalization (LN)、Instance Normalization (IN)、Group Normalization (GN)

他们的公式都是差不多的，就是减去均值，除以标准差，再施以线性映射。（只不过在对哪些维度求均值、方差，以及参数$\gamma$和$\beta$怎么对应有差异）

下图来自何凯明的论文：https://arxiv.org/pdf/1803.08494.pdf

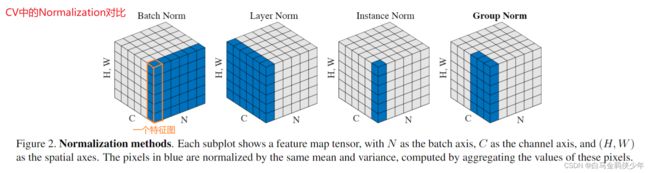
对于每一种Norm方法而言，每个像蓝色这样的区域会计算出一个均值和方差，在这个蓝色区域内的元素都会用这个均值和方差进行归一化。至于线性映射时参数$\gamma$和$\beta$怎么对应不同Norm时有差异的，我前面提到过BN和LN在这点上的差异。

下面这个例子来自博客：BatchNormalization、LayerNormalization、InstanceNorm、GroupNorm简介，我觉得举的例子很形象，就摘过来了。

---

计算机视觉(CV)领域的数据$x$一般是4维形式，如果把$x\in {\mathbb{R}}^{N\times C\times H\times W}$类比为一摞书，这摞书总共有 N 本，每本有 C 页，每页有 H 行，每行 W 个字符。

计算均值时

• BN 相当于把这些书按页码一一对应地加起来（例如：第1本书第36页，加第2本书第36页…），再除以每个页码下的字符总数：N×H×W，因此可以把 BN 看成求“平均书”的操作（注意这个“平均书”每页只有一个字）

• LN 相当于把每一本书的所有字加起来，再除以这本书的字符总数：C×H×W，即求整本书的“平均字”

• IN 相当于把一页书中所有字加起来，再除以该页的总字数：H×W，即求每页书的“平均字”

• GN 相当于把一本 C 页的书平均分成 G 份，每份成为有 C/G 页的小册子，对这个 C/G 页的小册子，求每个小册子的“平均字”

计算方差同理

此外，还需要注意它们的映射参数γ和β的区别：对于 BN，IN，GN， 其γ和β都是维度等于通道数 C 的向量。而对于 LN，其γ和β都是维度等于 normalized_shape 的矩阵。

最后，BN和IN 可以设置参数：momentum 和 track_running_stats来获得在全局数据上更准确的 running mean 和 running std。而 LN 和 GN 只能计算当前 batch 内数据的真实均值和标准差。

---

参考资料

[1] BatchNormalization、LayerNormalization、InstanceNorm、GroupNorm简介
[2] pytorch LayerNorm参数详解，计算过程
[3] PyTorch学习之归一化层（BatchNorm、LayerNorm、InstanceNorm、GroupNorm）
[4] BatchNorm详解：深入理解BatchNorm的原理、代码实现以及BN在CNN中的应用
[5] 深度神经网络架构【斯坦福21秋季：实用机器学习中文版】

写在最后

✨$原创不易，还希望各位大佬支持一下$

$点赞，你的认可是我创作的动力！$

⭐️ $收藏，你的青睐是我努力的方向！$

✏️ $评论，你的意见是我进步的财富！$