计算机视觉（一）：开篇

基本的图像操作和处理

1.1 PIL:Python图像处理类库

1.1.1 安装pil库

我的电脑之前就安装好pil库了所以可以直接开始敲代码了

1.1.2 基本处理

1. 读取图像
   读取一张小黄人图片
   open()函数用于创建PIL图像对象

from  PIL import Image
image = Image.open('yellow.jpg')
image.show()

2. 灰度图像

from  PIL import Image
image_g = Image.open('yellow.jpg').convert('L')
image_g.show()

3. 转换图片格式
save()方法用于保存图像到具有指定文件名的文件

for infile in filelist:
    outfile = os.path.splitext(infile)[0]+".jpg"
    if infile !=outfile:
        try:
            Image.open(infile).save(outfile)
        except IOError:
            print("Cannot convent",infile)

4. 创建缩略图
   thumbnail() 接收一个元组参数，这个参数指定生成缩略图的大小，然后将图像转换成符合元组参数指定大小的缩略图。
   thumbnail() 只能缩小，其改变对象的大小，返回值位none

from  PIL import Image
image = Image.open('yellow.jpg')
image.thumbnail((128,128))
image.show()

还是那只小黄人

5. 复制和粘贴图像区域

crop() 可以从一幅图像中裁剪指定区域。使用四元组来表示该区域。四元组的坐标依次是（左，上，右，下）。PIL中指定的坐标系的左上角坐标为（0，0）

box = (100,100,400,400)
region = image.crop(box)
region.show()

获得小黄人的一只眼睛

region = region.transpose(Image.ROTATE_180)
image.paste(region,box)
image.show()

接下来我们将这个区域旋转180°在放回原图中，获得以下小黄人

6.调整尺寸和旋转
调整一幅图的图像我们使用resize() 方法，resize() 与thumbnail() 相比，不会改变对象大小，只会返回一个新的Image对象。

out = image.resize((128,128))
out.show()

我们可以获得一个缩小版的小黄人

接下来在使用rotate旋转这个小黄人

out = image.resize((128,128))
out = out.rotate(45)
out.show()

1.2 Matplotlib

1.2.1 绘制图像、点和线

Matplotlib可以绘制出高质量的图表。
在脚本中==show()==命令首先打开图形用户界面，然后新建一个图像窗口。此界面会循环阻断脚步，然后暂停，直到最后一个图像窗口关闭。
代码：

from PIL import Image
from pylab import *

im = array(Image.open('yellow.jpg'))
imshow(im)

x = [100, 100, 400, 400]
y = [200, 500, 200, 500]

plot(x,y,'r*')

title('Plotting:“empire.jpg”‘)
axis('off') #使坐标轴不显示
show()

结果：

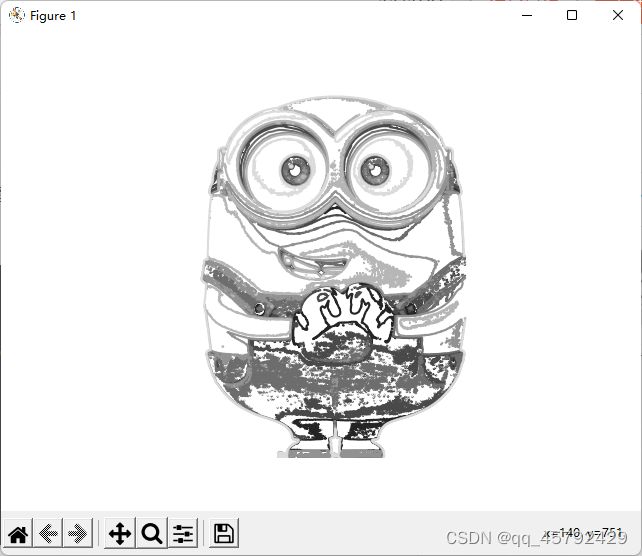
1.2.2 图像轮廓和直方图

1. 图像轮廓
   ==convert()==方法将图像转为灰度图像
   代码：

from PIL import Image
from pylab import *

im = array(Image.open('yellow.jpg').convert('L'))
figure()
# 不使用颜色信息
gray()
contour(im,origin ='image')
axis('equal')
axis('off')
show()

2. 直方图

hist() 函数的第二个参数指定小区间的数目。hist() 只接受一位数组作为输入，所以在绘制图像直方图之前，必须对图像进行压平处理。
flatten() 方法将任意数组按照行优先准则转换成一维数组。

from PIL import Image
from pylab import *

im = array(Image.open('yellow.jpg').convert('L'))
figure()
hist(im.flatten(),128)
show()

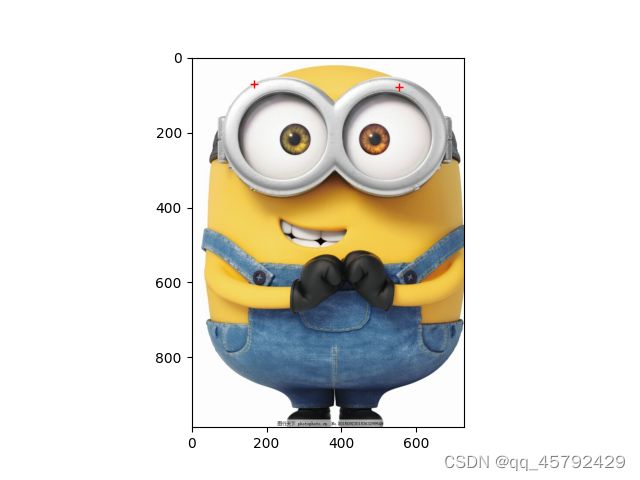
1.2.3 交互式标注

在Pylab库中我们可以使用ginput 函数实现交互式标注。当点击次数达到设定次数时，会将这些点击的坐标[x,y]自动保存至列表中。
代码：

from PIL import Image
from pylab import *

im = array(Image.open('yellow.jpg'))
imshow(im)
print('please click 3 points')
x = ginput(3)
print('you clicker:',x)
show()

1.3 Numpy

1.3.1 图像数组表示

Numpy中的数组对象是多维的。数组中的所有元素必须具有相同的数据类型。若创建数组对象时没有指定数据类型，数据类型会按照数据的类型自动确定。
灰度图像没有颜色信息，所以在形状元组中，只有两个数值
多个数组元素可以使用数组切片方式访问。
切片方式返回的是以指定间隔下标访问该数组的元素值。

负数切片表示从最后一个元素逆向计数。

1.3.2 灰度变换

根据某种目标条件按一定变换关系逐点改变源图像中每一个像素 灰度值 的方法。 目的是为了改善画质，使图像的显示效果更加清晰。
将图像读入NumPy数组对象后，我们可以对它们执行任意数学操作，一个简单的例子就是图像的灰度变换，考虑任意函数f，它将0~255映射到自身，也就是输出区间和输入区间相同

from PIL import Image
from pylab import *

im=array(Image.open('yellow.jpg').convert('L'))
print(int(im.min()),int(im.max()))

im2=255-im               #对图像进行反向处理
print(int(im2.min()),int(im2.max())) #查看最大/最小元素

im3=(100.0/255)*im+100   #将图像像素值变换到100...200区间
print(int(im3.min()),int(im3.max()))

im4=255.0*(im/255.0)**2  #对像素值求平方后得到的图像
print(int(im4.min()),int(im4.max()))

1.3.3 图像缩放

NumPy数组将成为我们对图像及数据进行处理的最主要工具，但是调整矩阵大小并没有一种简单的方法。我们可以用PIL图像对象转换写一个简单的图像尺寸调整函数

def imresize(im,sz):
    """    Resize an image array using PIL. """
    pil_im = Image.fromarray(uint8(im))

    return array(pil_im.resize(sz))

1.3.4 图像均衡化

直方图均衡化指将一幅图像的灰度直方图变平，使得变换后的图像中每个灰度值的分布概率都相同，该方法是对灰度值归一化的很好的方法，并且可以增强图像的对比度.
变换函数：图像中像素值的累积分布函数（cdf），将像素值的范围映射到目标范围的归一化操作

def histeq(im,nbr_bins=256):
  """ 对一幅灰度图像进行直方图均衡化"""

  # 计算图像的直方图
  imhist,bins = histogram(im.flatten(),nbr_bins,normed=True)
  cdf = imhist.cumsum()      # 累积分布函数
  cdf = 255 * cdf / cdf[-1]  # 归一化
  # 此处使用到累积分布函数cdf的最后一个元素（下标为-1），其目的是将其归一化到0~1范围

  # 使用累积分布函数的线性插值，计算新的像素值
  im2 = interp(im.flatten(),bins[:-1],cdf)

  return im2.reshape(im.shape), cdf

函数有两个输入参数：灰度函数、直方图中使用小区间的数目。函数返回直方图均衡化后的图像，以及用来做像素值映射的累积分布函数。函数中使用到累计分布函数的最后一个元素，目的是将其归一化到0…1范围。

1.3.5 图像平均

对图像取平均是一种图像降噪的简单方法，经常用于产生艺术效果。假设所有的图像具有相同的尺寸，我们可以对图像相同位置的像素相加取平均。

def compute_average(imlist):
  """ 计算图像列表的平均图像"""

  # 打开第一幅图像，将其存储在浮点型数组中
  averageim = array(Image.open(imlist[0]), 'f')

  for imname in imlist[1:]:
    try:
      averageim += array(Image.open(imname))
    except:
      print imname + '...skipped'
  averageim /= len(imlist)

  # 返回uint8 类型的平均图像
  return array(averageim, 'uint8')

有可能因为某些图像打不开而导致平均的结果只是某一幅自身或某两幅图像的平均

1.3.6 函数的主成分分析

PCA（Principal Component Analysis，主成分分析）是一个非常有用的降维技巧。它可以在使用尽可能少维数的前提下，尽量多地保持训练数据的信息，在此意义上是一个最佳技巧。即使是一幅 100×100 像素的小灰度图像，也有 10 000 维，可以看成 10 000 维空间中的一个点。一兆像素的图像具有百万维。由于图像具有很高的维数，在许多计算机视觉应用中，我们经常使用降维操作。PCA 产生的投影矩阵可以被视为将原始坐标变换到现有的坐标系，坐标系中的各个坐标按照重要性递减排列。
为了对图像数据进行 PCA 变换，图像需要转换成一维向量表示。我们可以使用 NumPy 类库中的flatten() 方法进行变换

from PIL import Image
from numpy import *

def pca(X):
  """ 主成分分析：
    输入：矩阵X ，其中该矩阵中存储训练数据，每一行为一条训练数据
    返回：投影矩阵（按照维度的重要性排序）、方差和均值"""

  # 获取维数
  num_data,dim = X.shape

  # 数据中心化
  mean_X = X.mean(axis=0)
  X = X - mean_X

if dim>num_data:
  # PCA- 使用紧致技巧
  M = dot(X,X.T) # 协方差矩阵
  e,EV = linalg.eigh(M) # 特征值和特征向量
  tmp = dot(X.T,EV).T # 这就是紧致技巧
  V = tmp[::-1] # 由于最后的特征向量是我们所需要的，所以需要将其逆转
  S = sqrt(e)[::-1] # 由于特征值是按照递增顺序排列的，所以需要将其逆转
  for i in range(V.shape[1]):
    V[:,i] /= S
else:
  # PCA- 使用SVD 方法
  U,S,V = linalg.svd(X)
  V = V[:num_data] # 仅仅返回前nun_data 维的数据才合理

# 返回投影矩阵、方差和均值
return V,S,mean_X

该函数首先通过减去每一维的均值将数据中心化，然后计算协方差矩阵对应最大特征值的特征向量，此时可以使用简明的技巧或者 SVD 分解。这里我们使用了 range() 函数，该函数的输入参数为一个整数 n，函数返回整数 0…(n-1) 的一个列表。你也可以使用 arange() 函数来返回一个数组，或者使用 xrange() 函数返回一个产生器（可能会提升速度）

如果数据个数小于向量的维数，我们不用 SVD 分解，而是计算维数更小的协方差矩阵 XXT 的特征向量。通过仅计算对应前 k（k 是降维后的维数）最大特征值的特征向量，可以使上面的 PCA 操作更快。由于篇幅所限，有兴趣的读者可以自行探索。矩阵 V 的每行向量都是正交的，并且包含了训练数据方差依次减少的坐标方向

import pickle
from PIL import Image
from numpy import *
from pylab import *
from PCV.tools import imtools,pca

# Uses sparse pca codepath

# 获取图像列表和尺寸
imlist=imtools.get_imlist('E:/python/Python Computer Vision/Image data/fontimages/a_thumbs')
# open ont image to get the size
im=array(Image.open(imlist[0]))
# get the size of the images
m,n=im.shape[:2]
# get the number of images
imnbr=len(imlist)
print("The number of images is %d" % imnbr)

# create matrix to store all flattened images
immatrix = array([array(Image.open(imname)).flatten() for imname in imlist],'f')

# PCA降维
V,S,immean=pca.pca(immatrix)

# 保存均值和主成分
#f = open('../ch01/font_pca_modes.pkl', 'wb')
#pickle.dump(immean,f)
#pickle.dump(V,f)
#f.close()

# Show the images (mean and 7 first modes)
# This gives figure 1-8 (p15) in the book.

figure()
gray()
subplot(241)
axis('off')
imshow(immean.reshape(m,n))
for i in range(7):
    subplot(2,4,i+2)
    imshow(V[i].reshape(m,n))
    axis('off')

show()

1.3.7 使用pickle模块

点云模块

如果想要保存一些结果或者数据以方便后续使用，Python 中的 pickle 模块非常有用。pickle模块可以接受几乎所有的 Python 对象，并且将其转换成字符串表示，该过程叫做封装（pickling）。从字符串表示中重构该对象，称为拆封（unpickling）。这些字符串表示可以方便地存储和传输

# 保存均值和主成分数据
f = open('font_pca_modes.pkl','wb')
pickle.dump(immean,f)
pickle.dump(V,f)
f.close()

许多对象可以保存到同一个文件中。pickle 模块中有很多不同的协议可以生成 .pkl 文件；如果不确定的话，最好以二进制文件的形式读取和写入

保存一个数组 x 到文件中：savetxt('test.txt',x,'%i')
读取可以使用:x = loadtxt('test.txt')

1.4 Scipy

建立在 NumPy 基础上，用于数值运算的开源工具包

1.4.1 图像模糊

图像的高斯模糊是非常经典的图像卷积例子。本质上，图像模糊就是将（灰度）图像I 和一个高斯核进行卷积操作

滤波操作模块——scipy.ndimage.filters

from PIL import Image
from numpy import *
from pylab import *
from scipy.ndimage import filters

im = array(Image.open('yellow.jpg').convert('L'))
im2 = filters.gaussian_filter(im,5)

1.4.2 图像导数

我们可以用离散近似的方式来计算图像的导数。图像导数大多数可以通过卷积简单地实现：
Ix=I∗Dx，Iy=I∗Dy
通常选择prewitt滤波器或sobel滤波器
这些导数滤波器可以使用scipy.ndimage.filters模块的标准卷积操作来简单实现

1.4.3 形态学：对象计数

形态学（或数学形态学）是度量和分析基本形状的图像处理方法的基本框架与集合。形态学通常用于处理二值图像，但是也能够用于灰度图像。二值图像是指图像的每个像素只能取两个值，通常是 0 和 1。二值图像通常是，在计算物体的数目，或者度量其大小时，对一幅图像进行阈值化后的结果
scipy.ndimage 中的 morphology 模块可以实现形态学操作
scipy.ndimage 中的measurements 模块来实现二值图像的计数和度量功能

from scipy.ndimage import measurements,morphology

# 载入图像，然后使用阈值化操作，以保证处理的图像为二值图像
im = array(Image.open('yellow.jpg').convert('L'))
im = 1*(im<128)

labels, nbr_objects = measurements.label(im)
print( "Number of objects:", nbr_objects)

首先载入该图像，通过阈值化方式来确保该图像是二值图像。通过和 1 相乘，脚本将布尔数组转换成二进制表示
然后，我们使用 label() 函数寻找单个的物体，并且按照它们属于哪个对象将整数标签给像素赋值
图像的灰度值表示对象的标签。可以看到，在一些对象之间有一些小的连接。进行二进制开（binary open）操作

# 形态学开操作更好地分离各个对象
im_open = morphology.binary_opening(im,ones((9,5)),iterations=2)

labels_open, nbr_objects_open = measurements.label(im_open)
print( "Number of objects:", nbr_objects_open)

binary_opening() 函数的第二个参数指定一个数组结构元素

from PIL import Image
from numpy import *
from scipy.ndimage import measurements, morphology
from pylab import *

"""   This is the morphology counting objects example in Section 1.4.  """

# 添加中文字体支持
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)

# load image and threshold to make sure it is binary
figure()
gray()
im = array(Image.open('E:/python/Python Computer Vision/Image data/houses.png').convert('L'))
subplot(221)
imshow(im)
axis('off')
title(u'原图', fontproperties=font)
im = (im < 128)

labels, nbr_objects = measurements.label(im)
print ("Number of objects:", nbr_objects)
subplot(222)
imshow(labels)
axis('off')
title(u'标记后的图', fontproperties=font)

# morphology - opening to separate objects better
im_open = morphology.binary_opening(im, ones((9, 5)), iterations=2)
subplot(223)
imshow(im_open)
axis('off')
title(u'开运算后的图像', fontproperties=font)

labels_open, nbr_objects_open = measurements.label(im_open)
print ("Number of objects:", nbr_objects_open)
subplot(224)
imshow(labels_open)
axis('off')
title(u'开运算后进行标记后的图像', fontproperties=font)

show()

输出：

Number of objects: 45
Number of objects: 48

from PIL import Image
from numpy import *
from scipy.ndimage import measurements, morphology
from pylab import *

"""   This is the morphology counting objects example in Section 1.4.  """



# load image and threshold to make sure it is binary
figure()
gray()
im = array(Image.open('yellow.jpg').convert('L'))
subplot(221)
imshow(im)
axis('off')
title(u'1')
im = (im < 128)

labels, nbr_objects = measurements.label(im)
print ("Number of objects:", nbr_objects)
subplot(222)
imshow(labels)
axis('off')
title(u'2')

# morphology - opening to separate objects better
im_open = morphology.binary_opening(im, ones((9, 5)), iterations=2)
subplot(223)
imshow(im_open)
axis('off')
title(u'3')

labels_open, nbr_objects_open = measurements.label(im_open)
print ("Number of objects:", nbr_objects_open)
subplot(224)
imshow(labels_open)
axis('off')
title(u'4')

show()

1.4.4 有用的Scipy模块

1.读写
data = scipy.io.loadmat(‘test.mat’)
上面代码中，data 对象包含一个字典，字典中的键对应于保存在原始 .mat 文件中的变量名。由于这些变量是数组格式的，因此可以很方便地保存到 .mat 文件中。你仅需创建一个字典（其中要包含你想要保存的所有变量），然后使用 savemat() 函数

data = {}
data['x'] = x
scipy.io.savemat('test.mat',data)

2.图像形式保存

from scipy.misc import imsave
imsave('test.jpg',im)

1.5 高级示例：图像去噪

图像去噪是在去除图像噪声的同时，尽可能地保留图像细节和结构的处理技术

from pylab import *
from numpy import *
from numpy import random
from scipy.ndimage import filters
from PCV.tools import rof


# create synthetic image with noise
im = zeros((500,500))
im[100:400,100:400] = 128
im[200:300,200:300] = 255
im = im + 30*random.standard_normal((500,500))

U,T = rof.denoise(im,im)
G = filters.gaussian_filter(im,10)


# plot
figure()
gray()

subplot(1,3,1)
imshow(im)
#axis('equal')
axis('off')
title(u'iamge')

subplot(1,3,2)
imshow(G)
#axis('equal')
axis('off')
title(u'after gauss')

subplot(1,3,3)
imshow(U)
#axis('equal')
axis('off')
title(u'after rof')

show()