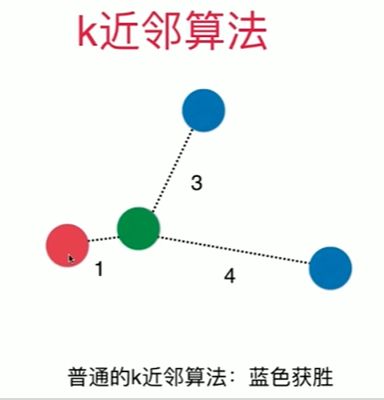
4-1 k近邻算法基础

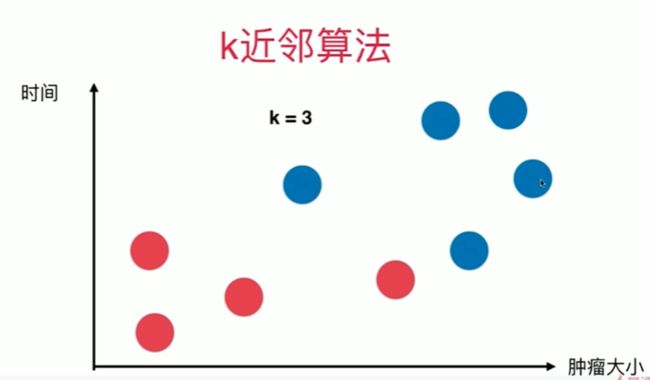


Notbook 示例
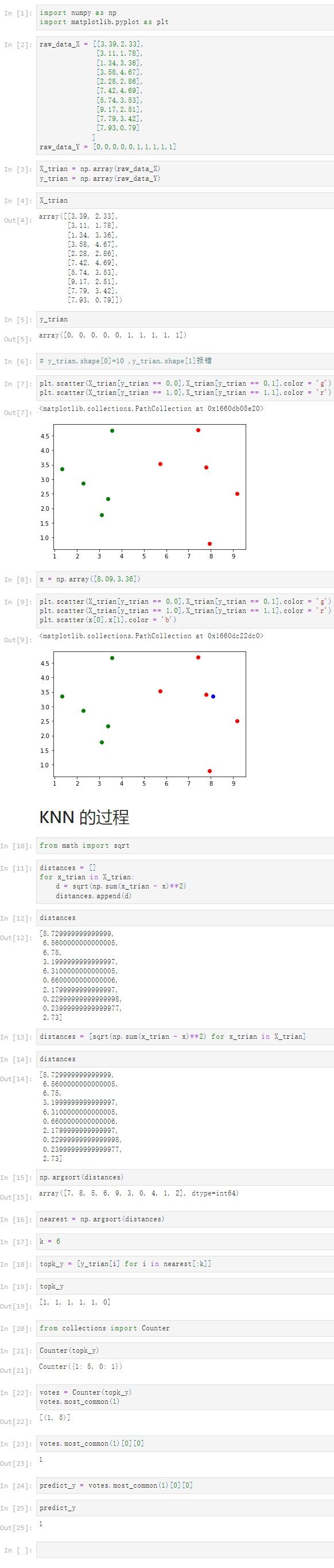
Notbook 源代码
import numpy as np
import matplotlib.pyplot as plt
[2]
raw_data_X = [[3.39,2.33],
[3.11,1.78],
[1.34,3.36],
[3.58,4.67],
[2.28,2.86],
[7.42,4.69],
[5.74,3.53],
[9.17,2.51],
[7.79,3.42],
[7.93,0.79]
]
raw_data_Y = [0,0,0,0,0,1,1,1,1,1]
[3]
X_trian = np.array(raw_data_X)
y_trian = np.array(raw_data_Y)
[4]
X_trian
array([[3.39, 2.33],
[3.11, 1.78],
[1.34, 3.36],
[3.58, 4.67],
[2.28, 2.86],
[7.42, 4.69],
[5.74, 3.53],
[9.17, 2.51],
[7.79, 3.42],
[7.93, 0.79]])
[5]
y_trian
array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])
[6]
# y_trian.shape[0]=10 ,y_trian.shape[1]报错
[7]
plt.scatter(X_trian[y_trian == 0,0],X_trian[y_trian == 0,1],color = 'g')
plt.scatter(X_trian[y_trian == 1,0],X_trian[y_trian == 1,1],color = 'r')
[8]
x = np.array([8.09,3.36])
[9]
plt.scatter(X_trian[y_trian == 0,0],X_trian[y_trian == 0,1],color = 'g')
plt.scatter(X_trian[y_trian == 1,0],X_trian[y_trian == 1,1],color = 'r')
plt.scatter(x[0],x[1],color = 'b')
KNN 的过程
[10]
from math import sqrt
[11]
distances = []
for x_trian in X_trian:
d = sqrt(np.sum(x_trian - x)**2)
distances.append(d)
[12]
distances
[5.729999999999999,
6.5600000000000005,
6.75,
3.1999999999999997,
6.3100000000000005,
0.6600000000000006,
2.1799999999999997,
0.22999999999999998,
0.23999999999999977,
2.73]
[13]
distances = [sqrt(np.sum(x_trian - x)**2) for x_trian in X_trian]
[14]
distances
[5.729999999999999,
6.5600000000000005,
6.75,
3.1999999999999997,
6.3100000000000005,
0.6600000000000006,
2.1799999999999997,
0.22999999999999998,
0.23999999999999977,
2.73]
[15]
np.argsort(distances)
array([7, 8, 5, 6, 9, 3, 0, 4, 1, 2], dtype=int64)
[16]
nearest = np.argsort(distances)
[17]
k = 6
[18]
topk_y = [y_trian[i] for i in nearest[:k]]
[19]
topk_y
[1, 1, 1, 1, 1, 0]
[20]
from collections import Counter
[21]
Counter(topk_y)
Counter({1: 5, 0: 1})
[22]
votes = Counter(topk_y)
votes.most_common(1)
[(1, 5)]
[23]
votes.most_common(1)[0][0]
1
[24]
predict_y = votes.most_common(1)[0][0]
[25]
predict_y
1
4-2 scikit-learn中的机器学习算法封装

Notbook 示例
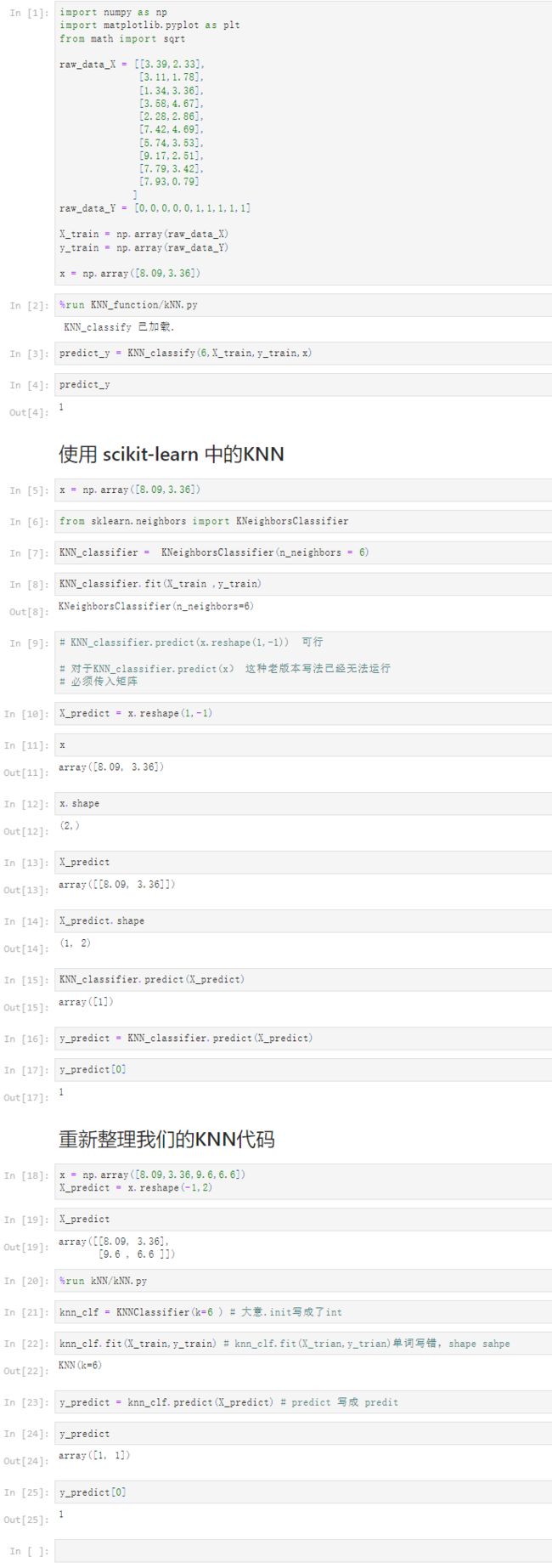
notbook 源码
[1]
import numpy as np
import matplotlib.pyplot as plt
from math import sqrt
raw_data_X = [[3.39,2.33],
[3.11,1.78],
[1.34,3.36],
[3.58,4.67],
[2.28,2.86],
[7.42,4.69],
[5.74,3.53],
[9.17,2.51],
[7.79,3.42],
[7.93,0.79]
]
raw_data_Y = [0,0,0,0,0,1,1,1,1,1]
X_train = np.array(raw_data_X)
y_train = np.array(raw_data_Y)
x = np.array([8.09,3.36])
[2]
%run KNN_function/kNN.py
KNN_classify 已加载.
[3]
predict_y = KNN_classify(6,X_train,y_train,x)
[4]
predict_y
1
使用 scikit-learn 中的KNN
[5]
x = np.array([8.09,3.36])
[6]
from sklearn.neighbors import KNeighborsClassifier
[7]
KNN_classifier = KNeighborsClassifier(n_neighbors = 6)
[8]
KNN_classifier.fit(X_train ,y_train)
KNeighborsClassifier(n_neighbors=6)
[9]
# KNN_classifier.predict(x.reshape(1,-1)) 可行
# 对于KNN_classifier.predict(x) 这种老版本写法已经无法运行
# 必须传入矩阵
[10]
X_predict = x.reshape(1,-1)
[11]
x
array([8.09, 3.36])
[12]
x.shape
(2,)
[13]
X_predict
array([[8.09, 3.36]])
[14]
X_predict.shape
(1, 2)
[15]
KNN_classifier.predict(X_predict)
array([1])
[16]
y_predict = KNN_classifier.predict(X_predict)
[17]
y_predict[0]
1
重新整理我们的KNN代码
[18]
x = np.array([8.09,3.36,9.6,6.6])
X_predict = x.reshape(-1,2)
[19]
X_predict
array([[8.09, 3.36],
[9.6 , 6.6 ]])
[20]
%run kNN/kNN.py
[21]
knn_clf = KNNClassifier(k=6 ) # 大意.init写成了int
[22]
knn_clf.fit(X_train,y_train) # knn_clf.fit(X_trian,y_trian)单词写错,shape sahpe
KNN(k=6)
[23]
y_predict = knn_clf.predict(X_predict) # predict 写成 predit
[24]
y_predict
array([1, 1])
[25]
y_predict[0]
1
4-3 训练数据集,测试数据集
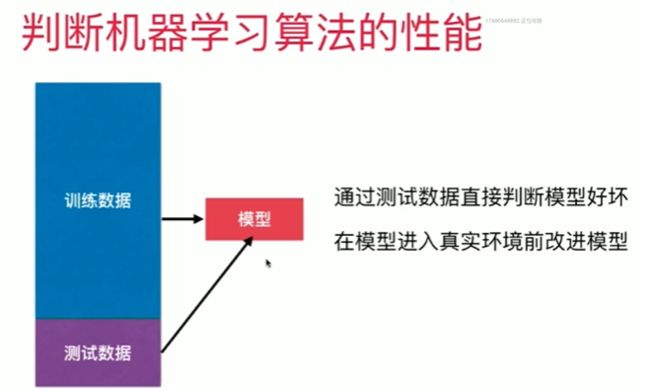

Notbook 示例
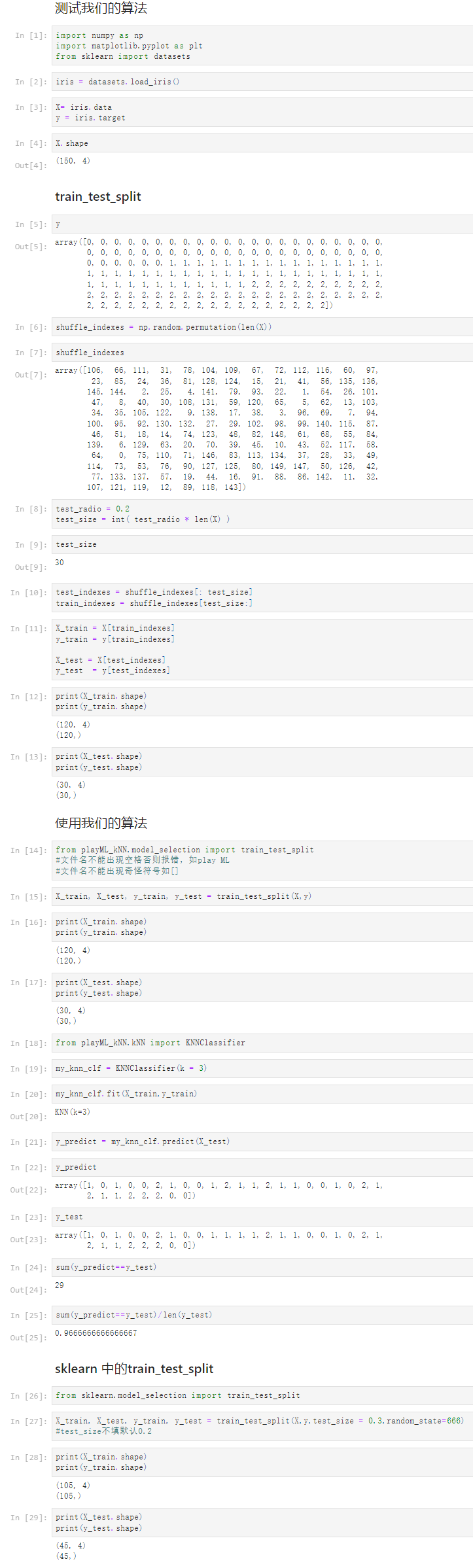
Notbook 源码
测试我们的算法
[1]
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
[2]
iris = datasets.load_iris()
[3]
X= iris.data
y = iris.target
[4]
X.shape
(150, 4)
train_test_split
[5]
y
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
[6]
shuffle_indexes = np.random.permutation(len(X))
[7]
shuffle_indexes
array([106, 66, 111, 31, 78, 104, 109, 67, 72, 112, 116, 60, 97,
23, 85, 24, 36, 81, 128, 124, 15, 21, 41, 56, 135, 136,
145, 144, 2, 25, 4, 141, 79, 93, 22, 1, 54, 26, 101,
47, 8, 40, 30, 108, 131, 59, 120, 65, 5, 62, 13, 103,
34, 35, 105, 122, 9, 138, 17, 38, 3, 96, 69, 7, 94,
100, 95, 92, 130, 132, 27, 29, 102, 98, 99, 140, 115, 87,
46, 51, 18, 14, 74, 123, 48, 82, 148, 61, 68, 55, 84,
139, 6, 129, 63, 20, 70, 39, 45, 10, 43, 52, 117, 58,
64, 0, 75, 110, 71, 146, 83, 113, 134, 37, 28, 33, 49,
114, 73, 53, 76, 90, 127, 125, 80, 149, 147, 50, 126, 42,
77, 133, 137, 57, 19, 44, 16, 91, 88, 86, 142, 11, 32,
107, 121, 119, 12, 89, 118, 143])
[8]
test_radio = 0.2
test_size = int( test_radio * len(X) )
[9]
test_size
30
[10]
test_indexes = shuffle_indexes[: test_size]
train_indexes = shuffle_indexes[test_size:]
[11]
X_train = X[train_indexes]
y_train = y[train_indexes]
X_test = X[test_indexes]
y_test = y[test_indexes]
[12]
print(X_train.shape)
print(y_train.shape)
(120, 4)
(120,)
[13]
print(X_test.shape)
print(y_test.shape)
(30, 4)
(30,)
使用我们的算法
[14]
from playML_kNN.model_selection import train_test_split
#文件名不能出现空格否则报错,如play ML
#文件名不能出现奇怪符号如[]
[15]
X_train, X_test, y_train, y_test = train_test_split(X,y)
[16]
print(X_train.shape)
print(y_train.shape)
(120, 4)
(120,)
[17]
print(X_test.shape)
print(y_test.shape)
(30, 4)
(30,)
[18]
from playML_kNN.kNN import KNNClassifier
[19]
my_knn_clf = KNNClassifier(k = 3)
[20]
my_knn_clf.fit(X_train,y_train)
KNN(k=3)
[21]
y_predict = my_knn_clf.predict(X_test)
[22]
y_predict
array([1, 0, 1, 0, 0, 2, 1, 0, 0, 1, 2, 1, 1, 2, 1, 1, 0, 0, 1, 0, 2, 1,
2, 1, 1, 2, 2, 2, 0, 0])
[23]
y_test
array([1, 0, 1, 0, 0, 2, 1, 0, 0, 1, 1, 1, 1, 2, 1, 1, 0, 0, 1, 0, 2, 1,
2, 1, 1, 2, 2, 2, 0, 0])
[24]
sum(y_predict==y_test)
29
[25]
sum(y_predict==y_test)/len(y_test)
0.9666666666666667
sklearn 中的train_test_split
[26]
from sklearn.model_selection import train_test_split
[27]
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3,random_state=666)
#test_size不填默认0.2
[28]
print(X_train.shape)
print(y_train.shape)
(105, 4)
(105,)
[29]
print(X_test.shape)
print(y_test.shape)
(45, 4)
(45,)
4-4 分类准确度
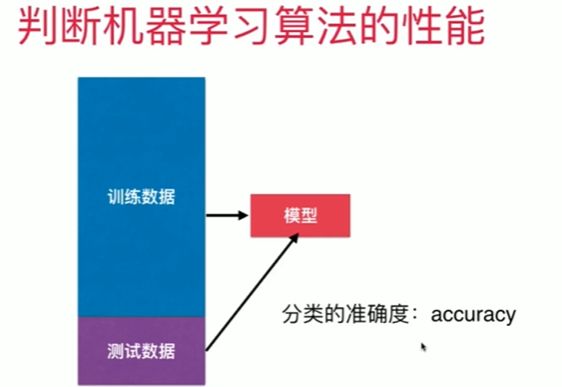
Notbook 示例

Notbook 源码
[1]
import numpy as np
import matplotlib
# from matplotlib import pyplotplot as plt 错误引用
import matplotlib.pyplot as plt
from sklearn import datasets
[2]
digits = datasets.load_digits()
[3]
digits.keys()
dict_keys(['data', 'target', 'frame', 'feature_names', 'target_names', 'images', 'DESCR'])
[4]
print(digits.DESCR)
.. _digits_dataset:
Optical recognition of handwritten digits dataset
--------------------------------------------------
**Data Set Characteristics:**
:Number of Instances: 1797
:Number of Attributes: 64
:Attribute Information: 8x8 image of integer pixels in the range 0..16.
:Missing Attribute Values: None
:Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)
:Date: July; 1998
This is a copy of the test set of the UCI ML hand-written digits datasets
https://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits
The data set contains images of hand-written digits: 10 classes where
each class refers to a digit.
Preprocessing programs made available by NIST were used to extract
normalized bitmaps of handwritten digits from a preprinted form. From a
total of 43 people, 30 contributed to the training set and different 13
to the test set. 32x32 bitmaps are divided into nonoverlapping blocks of
4x4 and the number of on pixels are counted in each block. This generates
an input matrix of 8x8 where each element is an integer in the range
0..16. This reduces dimensionality and gives invariance to small
distortions.
For info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.
T. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.
L. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,
1994.
.. topic:: References
- C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their
Applications to Handwritten Digit Recognition, MSc Thesis, Institute of
Graduate Studies in Science and Engineering, Bogazici University.
- E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.
- Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.
Linear dimensionalityreduction using relevance weighted LDA. School of
Electrical and Electronic Engineering Nanyang Technological University.
2005.
- Claudio Gentile. A New Approximate Maximal Margin Classification
Algorithm. NIPS. 2000.
[5]
X = digits.data
X.shape
(1797, 64)
[6]
y = digits.target
[7]
y.shape
(1797,)
[8]
digits.target_names # 无括号
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
[9]
y[:100]
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1,
2, 3, 4, 5, 6, 7, 8, 9, 0, 9, 5, 5, 6, 5, 0, 9, 8, 9, 8, 4, 1, 7,
7, 3, 5, 1, 0, 0, 2, 2, 7, 8, 2, 0, 1, 2, 6, 3, 3, 7, 3, 3, 4, 6,
6, 6, 4, 9, 1, 5, 0, 9, 5, 2, 8, 2, 0, 0, 1, 7, 6, 3, 2, 1, 7, 4,
6, 3, 1, 3, 9, 1, 7, 6, 8, 4, 3, 1])
[10]
X[:10]
array([[ 0., 0., 5., 13., 9., 1., 0., 0., 0., 0., 13., 15., 10.,
15., 5., 0., 0., 3., 15., 2., 0., 11., 8., 0., 0., 4.,
12., 0., 0., 8., 8., 0., 0., 5., 8., 0., 0., 9., 8.,
0., 0., 4., 11., 0., 1., 12., 7., 0., 0., 2., 14., 5.,
10., 12., 0., 0., 0., 0., 6., 13., 10., 0., 0., 0.],
[ 0., 0., 0., 12., 13., 5., 0., 0., 0., 0., 0., 11., 16.,
9., 0., 0., 0., 0., 3., 15., 16., 6., 0., 0., 0., 7.,
15., 16., 16., 2., 0., 0., 0., 0., 1., 16., 16., 3., 0.,
0., 0., 0., 1., 16., 16., 6., 0., 0., 0., 0., 1., 16.,
16., 6., 0., 0., 0., 0., 0., 11., 16., 10., 0., 0.],
[ 0., 0., 0., 4., 15., 12., 0., 0., 0., 0., 3., 16., 15.,
14., 0., 0., 0., 0., 8., 13., 8., 16., 0., 0., 0., 0.,
1., 6., 15., 11., 0., 0., 0., 1., 8., 13., 15., 1., 0.,
0., 0., 9., 16., 16., 5., 0., 0., 0., 0., 3., 13., 16.,
16., 11., 5., 0., 0., 0., 0., 3., 11., 16., 9., 0.],
[ 0., 0., 7., 15., 13., 1., 0., 0., 0., 8., 13., 6., 15.,
4., 0., 0., 0., 2., 1., 13., 13., 0., 0., 0., 0., 0.,
2., 15., 11., 1., 0., 0., 0., 0., 0., 1., 12., 12., 1.,
0., 0., 0., 0., 0., 1., 10., 8., 0., 0., 0., 8., 4.,
5., 14., 9., 0., 0., 0., 7., 13., 13., 9., 0., 0.],
[ 0., 0., 0., 1., 11., 0., 0., 0., 0., 0., 0., 7., 8.,
0., 0., 0., 0., 0., 1., 13., 6., 2., 2., 0., 0., 0.,
7., 15., 0., 9., 8., 0., 0., 5., 16., 10., 0., 16., 6.,
0., 0., 4., 15., 16., 13., 16., 1., 0., 0., 0., 0., 3.,
15., 10., 0., 0., 0., 0., 0., 2., 16., 4., 0., 0.],
[ 0., 0., 12., 10., 0., 0., 0., 0., 0., 0., 14., 16., 16.,
14., 0., 0., 0., 0., 13., 16., 15., 10., 1., 0., 0., 0.,
11., 16., 16., 7., 0., 0., 0., 0., 0., 4., 7., 16., 7.,
0., 0., 0., 0., 0., 4., 16., 9., 0., 0., 0., 5., 4.,
12., 16., 4., 0., 0., 0., 9., 16., 16., 10., 0., 0.],
[ 0., 0., 0., 12., 13., 0., 0., 0., 0., 0., 5., 16., 8.,
0., 0., 0., 0., 0., 13., 16., 3., 0., 0., 0., 0., 0.,
14., 13., 0., 0., 0., 0., 0., 0., 15., 12., 7., 2., 0.,
0., 0., 0., 13., 16., 13., 16., 3., 0., 0., 0., 7., 16.,
11., 15., 8., 0., 0., 0., 1., 9., 15., 11., 3., 0.],
[ 0., 0., 7., 8., 13., 16., 15., 1., 0., 0., 7., 7., 4.,
11., 12., 0., 0., 0., 0., 0., 8., 13., 1., 0., 0., 4.,
8., 8., 15., 15., 6., 0., 0., 2., 11., 15., 15., 4., 0.,
0., 0., 0., 0., 16., 5., 0., 0., 0., 0., 0., 9., 15.,
1., 0., 0., 0., 0., 0., 13., 5., 0., 0., 0., 0.],
[ 0., 0., 9., 14., 8., 1., 0., 0., 0., 0., 12., 14., 14.,
12., 0., 0., 0., 0., 9., 10., 0., 15., 4., 0., 0., 0.,
3., 16., 12., 14., 2., 0., 0., 0., 4., 16., 16., 2., 0.,
0., 0., 3., 16., 8., 10., 13., 2., 0., 0., 1., 15., 1.,
3., 16., 8., 0., 0., 0., 11., 16., 15., 11., 1., 0.],
[ 0., 0., 11., 12., 0., 0., 0., 0., 0., 2., 16., 16., 16.,
13., 0., 0., 0., 3., 16., 12., 10., 14., 0., 0., 0., 1.,
16., 1., 12., 15., 0., 0., 0., 0., 13., 16., 9., 15., 2.,
0., 0., 0., 0., 3., 0., 9., 11., 0., 0., 0., 0., 0.,
9., 15., 4., 0., 0., 0., 9., 12., 13., 3., 0., 0.]])
[11]
some_digit = X[666]
[12]
y[666]
0
[13]
some_digit_image = some_digit.reshape(8,8)
plt.imshow(some_digit_image,cmap = matplotlib.cm.binary) # 无须plot.show
[14]
from playML.model_selection import train_test_split
[15]
X_train, X_test, y_train, y_test = train_test_split(X,y,test_radio = 0.2)
[16]
from playML.kNN import KNNClassifier
[17]
my_knn_clf = KNNClassifier(k = 3)
[18]
my_knn_clf.fit(X_train,y_train)
KNN(k=3)
[19]
y_predict = my_knn_clf.predict(X_test)
[20]
y_predict
array([7, 7, 2, 6, 4, 2, 7, 0, 0, 5, 0, 3, 2, 1, 5, 4, 0, 5, 6, 7, 7, 7,
6, 0, 9, 6, 5, 5, 6, 3, 3, 1, 5, 8, 8, 2, 2, 4, 7, 0, 5, 4, 3, 2,
1, 8, 4, 5, 9, 5, 0, 7, 3, 0, 5, 4, 3, 7, 1, 2, 1, 1, 5, 7, 3, 0,
2, 3, 7, 1, 9, 3, 9, 0, 5, 8, 0, 6, 0, 9, 8, 3, 2, 0, 4, 1, 9, 6,
4, 0, 6, 2, 6, 4, 4, 2, 4, 1, 5, 2, 7, 1, 4, 9, 0, 4, 3, 8, 5, 7,
8, 2, 0, 7, 0, 3, 0, 7, 9, 5, 9, 9, 8, 2, 7, 7, 8, 5, 5, 8, 2, 6,
0, 5, 2, 6, 1, 6, 2, 6, 3, 9, 8, 4, 5, 4, 6, 2, 3, 1, 4, 9, 7, 6,
2, 4, 1, 4, 3, 8, 6, 7, 7, 3, 3, 0, 0, 6, 7, 4, 9, 0, 3, 2, 7, 8,
5, 4, 4, 0, 7, 6, 5, 1, 1, 3, 9, 3, 8, 7, 0, 1, 5, 0, 6, 5, 7, 4,
7, 6, 2, 0, 4, 9, 7, 2, 7, 9, 0, 2, 7, 9, 2, 1, 8, 4, 8, 9, 4, 3,
5, 9, 8, 8, 0, 4, 3, 2, 2, 5, 2, 4, 9, 2, 7, 3, 6, 4, 4, 1, 6, 3,
1, 4, 9, 1, 9, 0, 3, 9, 2, 8, 3, 5, 4, 6, 4, 5, 4, 6, 6, 8, 0, 3,
8, 7, 0, 7, 9, 2, 3, 2, 2, 1, 5, 9, 6, 6, 0, 0, 8, 3, 2, 1, 9, 4,
8, 6, 1, 2, 0, 8, 7, 2, 5, 9, 3, 9, 6, 6, 2, 8, 5, 6, 2, 6, 6, 7,
1, 8, 2, 2, 4, 3, 4, 0, 8, 1, 7, 1, 2, 9, 9, 2, 1, 3, 7, 8, 7, 6,
1, 8, 3, 7, 2, 6, 3, 2, 3, 9, 4, 1, 7, 6, 3, 7, 9, 0, 9, 0, 9, 3,
5, 0, 6, 4, 8, 9, 4])
[21]
sum(y_predict == y_test)/len(y_test)
0.9916434540389972
[22]
from playML.metrics import accuracy_score
[23]
accuracy_score(y_test,y_predict)
0.9916434540389972
[24]
my_knn_clf.score(X_test,y_test)
0.9916434540389972
scikit_learn 中的 accuracy_score
[25]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3,random_state=666)
[26]
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier(n_neighbors = 6) # n_neighbors == 6 ,写成两个等号
[27]
knn_clf.fit(X_train,y_train)
KNeighborsClassifier(n_neighbors=6)
[28]
y_predict = knn_clf.predict(X_test)
from sklearn.metrics import accuracy_score
[29]
accuracy_score(y_test,y_predict)
0.9888888888888889
[30]
knn_clf.score(X_test,y_test)
0.9888888888888889
4-5 超参数







Notbook 示例
Notbook 源码
[1]
import numpy as np
from sklearn import datasets
[2]
digits = datasets.load_digits()
X = digits.data
y = digits.target
[3]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3 ,random_state=666 ) # ,random_state=666
[4]
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier( n_neighbors = 6 )
knn_clf.fit(X_train,y_train)
knn_clf.score(X_test,y_test)
0.9888888888888889
寻找最好的K
[5]
best_score = 0.0
best_k = -1
for k in range(1,11):
knn_clf = KNeighborsClassifier( n_neighbors = k )
knn_clf.fit(X_train,y_train)
score = knn_clf.score(X_test,y_test)
if score > best_score:
best_k = k
best_score = score
print("best_k = ", best_k)
print("best_score = ", best_score)
best_k = 3
best_score = 0.9888888888888889
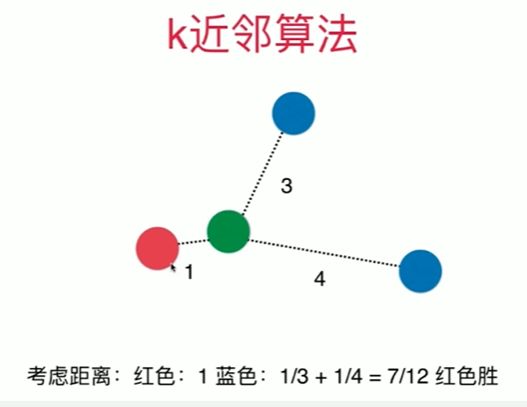
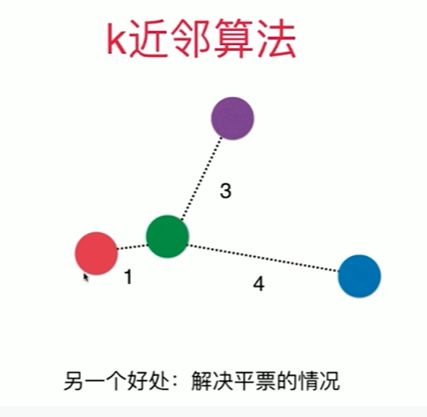
考虑距离? 不考虑距离?
[6]
best_method = ""
best_k = -1
best_score = 0.0
# 若无 best_score = 0.0 局部变量赋值,出来等于无
# uniform 不考虑距离的权重,distance考虑权重一般取倒数
for method in ["uniform", "distance"]: # unifrom 为错
# print(method)
for k in range(1,11):
#print(k)
knn_clf = KNeighborsClassifier( n_neighbors = k,weights = method)
knn_clf.fit(X_train,y_train)
score = knn_clf.score(X_test,y_test)
if score > best_score:
best_k = k
best_score = score
best_method = method
print("best_method = ",best_method)
print("best_k = ", best_k)
print("best_score = ", best_score)
best_method = uniform
best_k = 3
best_score = 0.9888888888888889
改变随机数对结果的影响是巨大的
random_state=222 时,best_method = distance best_k = 8 best_score = 0.9888888888888889
搜索明可夫斯基距离相应的P
[7]
%%time
best_p = -1
best_k = -1
best_score = 0.0
for k in range(1,11):
for p in range(1,6):
knn_clf = KNeighborsClassifier( n_neighbors = k,weights = "distance",p = p)
knn_clf.fit(X_train,y_train)
score = knn_clf.score(X_test,y_test)
if score > best_score:
best_k = k
best_score = score
best_p = p
print("best_p = ",best_p)
print("best_k = ", best_k)
print("best_score = ", best_score)
best_p = 2
best_k = 3
best_score = 0.9888888888888889
CPU times: total: 1min 13s
Wall time: 1min 19s
%%time
best_p = -1
best_method = ""
best_k = -1
best_score = 0.0
# 若无 best_score = 0.0 则不会进入判断中的赋值语句
for method in ["uniform", "distance"]: # unifrom 为错
# print(method)
for k in range(1,11):
for p in range(1,6):
#print(k)
knn_clf = KNeighborsClassifier( n_neighbors = k,weights = method,p=p)
knn_clf.fit(X_train,y_train)
score = knn_clf.score(X_test,y_test)
if score > best_score:
best_k = k
best_score = score
best_method = method
best_p = p
print("best_method = ",best_method)
print("best_k = ", best_k)
print("best_score = ", best_score)
print("best_p = ",best_p)
P 只有在 weights 为 distance 的时候才有意义 ?























