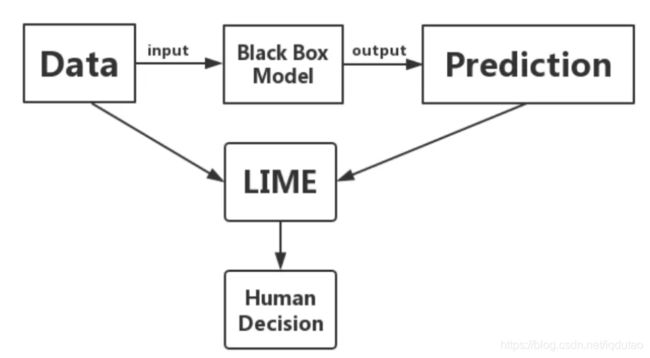
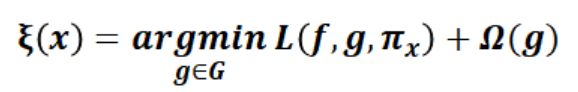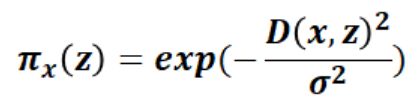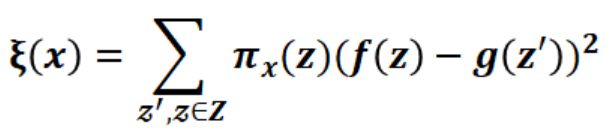模型可解释性-LIME

 

        在算法建模过程中，我们一般会用测试集的准确率与召回率衡量一个模型的好坏。但在和客户的实际沟通时，单单抛出一个数字就想要客户信任我们，那肯定是不够的，这就要求我们摆出规则，解释模型。但不是所有的模型都是规则模型，一些黑盒模型（比如神经网络）有着更高的准确率，但是无法给出具体的规则，无法让普通人理解和信任模型的预测结果。尤其当模型应用到银行业等金融领域时，透明度和可解释性是机器学习模型是否值得信任的重要考核标准。我们需要告诉业务人员如何营销，告诉风控人员如何识别风险点，而不仅仅告诉他们预测的结果。一个预测表现接近完美、却属于黑盒的人工智能模型，会容易产生误导的决策，还可能招致系统性风险，导致漏洞被攻击，因而变得不安全可靠。因此我们需要建立一个解释器来解释黑盒模型，并且这个解释器必须满足以下特征：

可解释性

要求解释器的模型与特征都必须是可解释的，像决策树、线性模型都是很适合拿来解释的模型；而可解释的模型必须搭配可解释的特征，才是真正的可解释性，让不了解机器学习的人也能通过解释器理解模型。

局部保真度

既然我们已经使用了可解释的模型与特征，就不可能期望简单的可解释模型在效果上等同于复杂模型（比如原始CNN分类器）。所以解释器不需要在全局上达到复杂模型的效果，但至少在局部上效果要很接近，而此处的局部代表我们想观察的那个样本的周围。

与模型无关

这里所指的是与复杂模型无关，换句话说无论多复杂的模型，像是SVM或神经网络，该解释器都可以工作。

除了传统的特征重要性排序外，ICE、PDP、SDT、LIME、SHAP都是揭开机器学习模型黑箱的有力工具。

• 特征重要性计算依据某个特征进行决策树分裂时，分裂前后的信息增益（基尼系数）；
• ICE和PDP考察某项特征的不同取值对模型输出值的影响；
• SDT用单棵决策树解释其它更复杂的机器学习模型；
• LIME的核心思想是对于每条样本，寻找一个更容易解释的代理模型解释原模型；
• SHAP的概念源于博弈论，核心思想是计算特征对模型输出的边际贡献；

 

模型可解释性-SHAPE

模型可解释性-LIME

模型可解释性-树结构可视化

 

目录

LIME的原理

LIME具体计算步骤

LIME逻辑示例

LIME算法优缺点

应用实例

LIME代码

---

LIME的原理

LIME（Local Interpretable Model-agnostic Explanations）的缩写。通过名字便可以看出，该模型是一个局部可解释模型，并且是一个与模型自身的无关的可解释方法。使用训练的局部代理模型来对单个样本进行解释。假设对于需要解释的黑盒模型，取关注的实例样本，在其附近进行扰动生成新的样本点，并得到黑盒模型的预测值，使用新的数据集训练可解释的模型（如线性回归、决策树），得到对黑盒模型良好的局部近似。名字的每一部分反映了我们进行解释的意图。其名称也很好的反应了它的特点：

Local: 基于想要解释的预测值及其附近的样本，构建局部的线性模型或其他代理模型；

Interpretable: LIME做出的解释易被人类理解。利用局部可解释的模型对黑盒模型的预测结果进行解释，构造局部样本特征和预测结果之间的关系；

Model-Agnostic: LIME解释的算法与模型无关，无论是用Random Forest、SVM还是XGBoost等各种复杂的模型，得到的预测结果都能使用LIME方法来解释；

Explanations: LIME是一种事后解释方法；

该作者提出了解释器需要满足的四个条件：

• 可解释性： 对模型和特征两个方面都有要求。决策树、线性回归和朴素贝叶斯都是具有可解释的模型，前提是特征也要容易解释才行。否则像是词嵌入（Word Embedding）的方式，即使是简单的线性回归也无法做到可解释性。而且解释性还要取决于目标群体，比如向不了解模型的业务人员去解释这些模型。相比之下，线性模型也要比简单的贝叶斯更容易理解。
• 局部忠诚（ local fidelity）：既然我们已经使用了可解释的模型与特征，就不可能期望简单的可解释模型在效果上等同于复杂模型（比如原始CNN分类器）。所以解释器不需要在全局上达到复杂模型的效果，但至少在局部上效果要很接近，而此处的局部代表我们想观察的那个样本的周围。
• 与模型无关： 任何其他模型，像是SVM或神经网络，该解释器都可以工作。
• 全局视角： 准确度，AUC等有时并不是一个很好的指标，我们需要去解释模型。解释器的工作在于提供对样本的解释，来帮助人们对模型产生信任。

LIME的思想很简单，我们希望使用简单的模型来对复杂的模型进行解释。这里简单的模型可以是线性模型，因为我们可以通过查看线性模型的系数大小来对模型进行解释，在这里，LIME只会对每一个样本进行解释(explain individual predictions)。LIME会产生一个新的数据集(这个数据集我们是通过对某一个样本数据进行变换得到)，接着在这个新的数据集上， 我们训练一个简单模型(容易解释的模型)，我们希望简答模型在新数据集上的预测结果和复杂模型在该数据集上的预测结果是相似的。

LIME可处理不同类型的输入数据，如表格数据(Tabular Data)、图像数据（Image Data）或文本数据(Text Data)。对于表格数据，如用银行客户行为数据预测理财产品销售，训练完复杂模型后可以用LIME得到哪些特征影响理财产品销售；图像数据，如识别图片中的动物是否为猫，训练完复杂模型后可以用LIME得到图片中的动物被识别为猫是因为哪一个或几个像素块；文本数据，如识别短信是否为垃圾短信，训练完复杂模型后可以用LIME得到一条信息被判断为垃圾短信是因为哪一个或几个关键词。

为了做到与模型无关，LIME不会深入模型内部。为了搞清楚哪一部分输入对预测结果产生贡献，我们将输入值在其周围做微小的扰动，观察模型的预测行为。然后我们根据这些扰动的数据点距离原始数据的距离分配权重，基于它们学习得到一个可解释的模型和预测结果。

LIME具体计算步骤

（1）目标函数：

解释模型定义为模型g∈G，我们进一步使用πx（z）作为实例z与x之间的接近度，以定义x周围的局部性。定义一个目标函数ξ，这里的L函数作为一个度量，描述如何通过πx在局部定义中，不忠诚的g如何逼近f（复杂模型），在当Ω(g)(解释模型复杂度)足够低可以被人类理解时，我们最小化L函数得到目标函数的最优解。LIME产生的解释如下：

上式中每一个字母的含义:

• f表示原始的模型, 即需要解释的模型.
• g表示简单模型, G是简单模型的一个集合, 如所有可能的线性模型.
• Pi_x表示我们新数据集中的数据x'与原始数据instance x的距离.
• Ω(g)表示模型g的复杂程度.

（2）引入相似度后的目标函数：

对这个样本进行可解释的扰动，论文中还对扰动前后的样本相似度的距离进行了定义，这取决于样本的类型（文本的话就是余弦相似性，图像的话就是L2范数距离）。则相似度计算公式如下：

（3）最终函数：

有了相似度的定义，便可以将原先的目标函数改写成如下的形式。其中f(z)就是扰动样本，在d维空间（原始特征）上的预测值，并把该预测值作为答案，g(z’)则是在d’维空间（可解释特征）上的预测值，然后以相似度作为权重，因此上述的目标函数便可以通过线性回归的方式进行优化。

于是整个LIME的步骤如下(即训练模型G的步骤)

• 对整个数据进行训练，模型可以是Lightgbm，XGBoost等复杂的模型（本身不可解释）;
• 选择我们想要解释的变量X;
• 对数据集中的数据进行可解释的N次扰动，生成局部样本;
• 对这些新的Sample求出权重，这个权重是这些数据点与我们要解释的数据之间的距离;
• 根据上面新的数据集，拟合一个简单的模型G，比如Lasso Regression得到模型的权重;
• 通过简单模型G来对原复杂模型在X点附近进行解释;

LIME逻辑示例

示例1 如下：

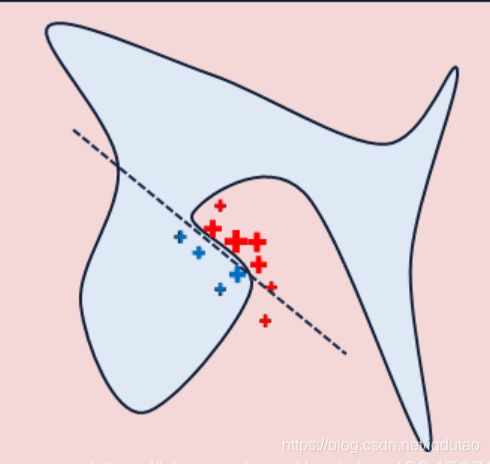
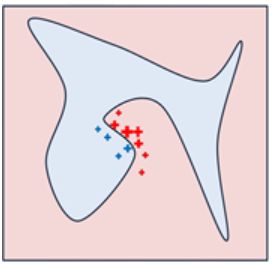
原始模型的决策函数用蓝/粉背景表示，显然是非线性的。亮红色的叉叉表示被解释的样本（称为X）。我们在X周围采样，按照它们到X的距离赋予权重（这里权重的意思是尺寸）。我们用原始模型预测这些扰动过的样本，然后学习一个线性模型（虚线）在X附近很好地近似模型。注意，这个解释只在X附近成立，对全局无效。

示例2 如下：

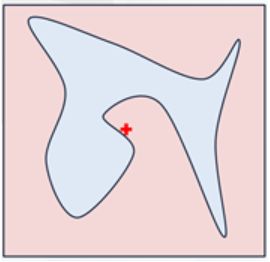
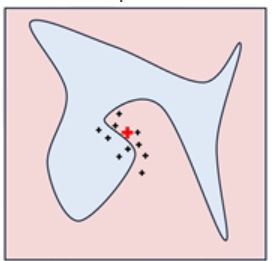
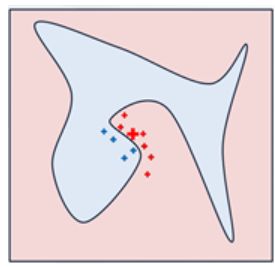
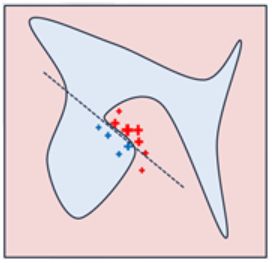
如图所示，红色和蓝色区域表示一个复杂的分类模型（黑盒），图中加粗的红色十字表示需要解释的样本，显然，我们很难从全局用一个可解释的模型（例如线性模型）去逼近拟合它。但是，当我们把关注点从全局放到局部时，可以看到在某些局部是可以用线性模型去拟合的。具体来说，我们从加粗的红色十字样本周围采样，所谓采样就是对原始样本的特征做一些扰动，将采样出的样本用分类模型分类并得到结果（红十字和蓝色点），同时根据采样样本与加粗红十字的距离赋予权重（权重以标志的大小表示）。虚线表示通过这些采样样本学到的局部可解释模型，在这个例子中就是一个简单的线性分类器。在此基础上，我们就可以依据这个局部的可解释模型对这个分类结果进行解释了。

具体过程为：

（1）首先要有一个好的分类器（复杂模型）
（2）选定一个要解释的样本x，以及在可解释纬度上的x’

（3）定义一个相似度计算方式，以及要选取的K个特征来解释。
（4）进行N次perturb扰动，z’，从x’扰动而来。

（5）将z‘还原到d维度，并计算预测值f(z)以及相似度。

（6）根据距离进行加权

（7）收集到N次扰动的样本后，利用岭回归取得对这个样本有影响力的系数。

那么我们如何对数据集进行扰动来得到新的数据， 对于表格数据, 我们可以分别扰动每一个特征， 从一个正态分布(均值和方差为这个特征的均值和方差)中进行随机抽样。 这样做会有一个问题，即不是从我们要解释的数据为中心进行采样， 而是从整个数据集的中心进行采样。 (LIME samples are not taken around the instance of interest, but from the training data's mass center, which is problematic)

LIME算法优缺点

（1）LIME算法有很强的通用性，效果好。LIME除了能够对图像的分类结果进行解释外，还可以应用到自然语言处理的相关任务中，如主题分类、词性标注等。因为LIME本身的出发点就是模型无关的，具有广泛的适用性。

（2）LIME算法速度慢，LIME在采样完成后，每张采样出来的图片都要通过原模型预测一次结果，所以在速度上没有明显优势。

（3）LIME算法拓展方向，本文的作者在18年新提出了Anchors的方法，指的是复杂模型在局部所呈现出来的很强的规则性的规律，注意和LIME的区别，LIME是在局部建立一个可理解的线性可分模型，而Anchors的目的是建立一套更精细的规则系统。在和文本相关的任务上有不错的表现。有待我们继续研究。

优点：

1. 表格型数据、文本和图片均适用；
2. 解释对人友好，容易明白；
3. 给出一个忠诚性度量，判断可解释模型是否可靠；
4. LIME可以使用原模型所用不到的一些特征数据，比如文本中一个词是否出现。

缺点：

1. 表格型数据中，相邻点很难定义，需要尝试不同的kernel来看LIME给出的可解释是否合理；
2. 扰动时，样本服从高斯分布，忽视了特征之间的相关性；
3. 稳定性不够好，重复同样的操作，扰动生成的样本不同，给出的解释可能会差别很大。

应用实例

示例1：以树蛙图像分类为例，将LIME的过程展示一遍。
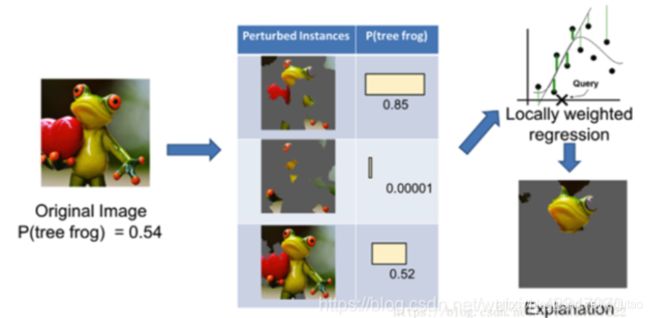
下图为我们假设的CNN模型的预测结果，预测一张图片中可能有哪些物体。模型此时告诉我们有54%的概率这张图像是一只树蛙，但也有7%的概率是台球和5%的概率是热气球。现在我们想使用LIME来理解模型为何做出下图的判断。

先把原始图片转成可解释的特征表示，通过可解释的特征表示对样本进行扰动，得到N个扰动后的样本。然后再将这N个样本还原到原始特征空间，并把预测值作为真实值，用可解释的特征数据表示建立简单的数据表示，观察哪些超像素的系数较大

将这些较大的系数进行可视化可以得到下图的样子，从而理解模型为什么会做出这种判断。青蛙的眼睛和台球很相似，特别是在绿色的背景下。同理红色的心脏也与热气球类似。

示例2：以二分类为例，将LIME的过程展示一遍。

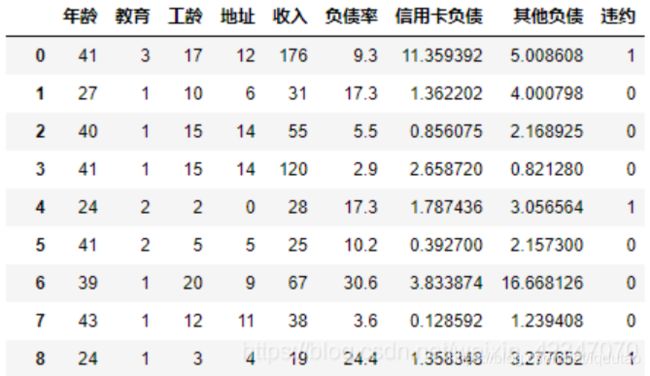
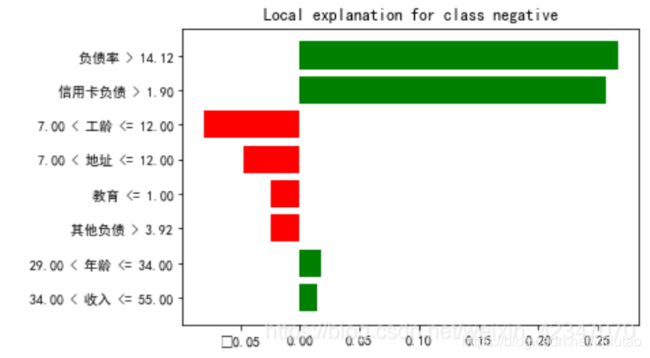
现在有一批名单，特征包括年龄、职业、教育、工龄、收入等字段，来判断目标是否会产生违约。在利用随机森林建模得出判断结果后，可以利用LIME算法来查看目标个体在模型中被分类的理由。

选择第81个样本利用LIME解释器解释规则，发现特征负债率与信用卡负债是支持模型判断该样本为违约的主要理由：

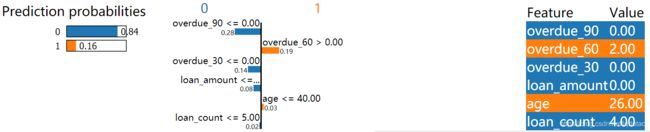
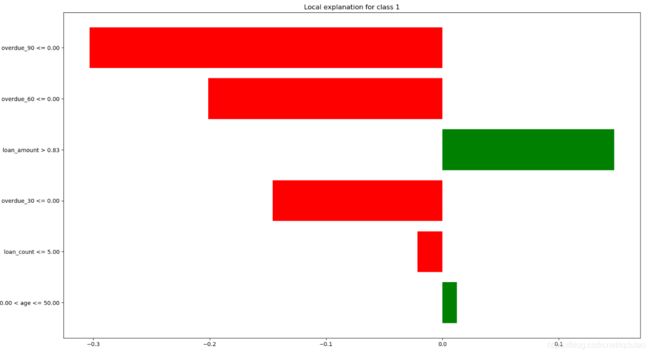
示例3：信用卡违约二分类

本测试数据来源于kaggle上一个很经典的评分卡案例 Give Me Some Credit ，通过改进信用评分技术，预测未来两年借款人会遇到财务困境的可能性。银行在市场经济中发挥关键作用。 他们决定谁可以获得融资，以及以何种条件进行投资决策。 为了市场和社会的运作，个人和公司需要获得信贷。信用评分算法可以猜测违约概率，这是银行用于确定是否应授予贷款的方法。目标是建立一个借款人可以用来帮助做出最佳财务决策的模型。

数据来源：https://www.kaggle.com/c/GiveMeSomeCredit/data

数据集介绍说明：

数据集示例：

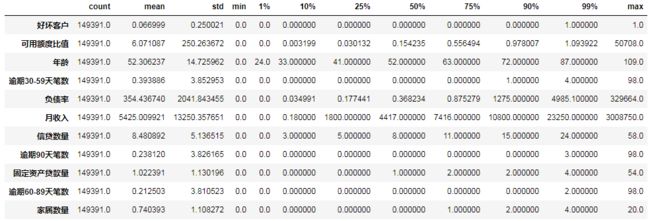
数据集统计：

LIME代码

import lime.lime_tabular
def feature_select_lime_plot(x_train,model,plot_name,data_predict):
    feature_names = x_train.columns.values
    target_names = ['0', '1']

    #生成解释器
    explainer = lime.lime_tabular.LimeTabularExplainer(x_train.values,
                                                       feature_names=feature_names,
                                                       class_names=target_names,
                                                       discretize_continuous=True)
    #对预测数据（局部）解释
    exp = explainer.explain_instance(data_predict.values, model.predict_proba, num_features=6)
    exp.save_to_file('plot_feature_'+plot_name+ '_predict_lime.html')
    exp.as_pyplot_figure()
    plt.savefig('plot_feature_'+plot_name+ '_predict_lime_detail.png')
    plt.clf()
    print('lime 变量预测已经完成 ----------')

 

 

 

参考链接：https://uzshare.com/view/827734
参考链接：https://uzshare.com/view/827734
参考链接：https://zhuanlan.zhihu.com/p/64799119
参考链接：https://cloud.tencent.com/developer/news/617057
参考链接：https://mathpretty.com/10699.html
参考链接：https://mathpretty.com/11210.html