LC-1201. 丑数 III（二分法、容斥原理）

1201. 丑数 III

难度中等

给你四个整数：n 、a 、b 、c ，请你设计一个算法来找出第 n 个丑数。

丑数是可以被 a 或 b 或 c 整除的 正整数 。

示例 1：

输入：n = 3, a = 2, b = 3, c = 5
输出：4
解释：丑数序列为 2, 3, 4, 5, 6, 8, 9, 10... 其中第 3 个是 4。

示例 2：

输入：n = 4, a = 2, b = 3, c = 4
输出：6
解释：丑数序列为 2, 3, 4, 6, 8, 9, 10, 12... 其中第 4 个是 6。

示例 3：

输入：n = 5, a = 2, b = 11, c = 13
输出：10
解释：丑数序列为 2, 4, 6, 8, 10, 11, 12, 13... 其中第 5 个是 10。

示例 4：

输入：n = 1000000000, a = 2, b = 217983653, c = 336916467
输出：1999999984

提示：

• 1 <= n, a, b, c <= 10^9
• 1 <= a * b * c <= 10^18
• 本题结果在 [1, 2 * 10^9] 的范围内

容斥原理+二分法

本题的关键是对于选中的值x，得出x是丑数序列中的第几个丑数。

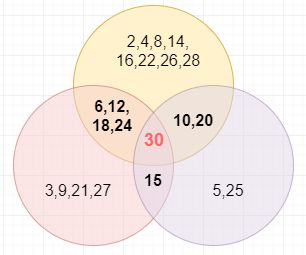
我们这里需要用到容斥原理。

举例：a = 2, b = 3, c = 5

则指定数字x范围内的丑数数量为：

long count = x/a + x/b + x/c - x/lcm_ab - x / lcm_ac - x / lcm_bc + x / lcm_abc;

这里的lcm的含义为最小公倍数。

// 求最小公倍数
private long lcm(long a, long b) {
    return a * 1L * (b / gcd(a, b));
}

// 求最大公约数
private long gcd(long a, long b) {
    return b == 0 ? a : gcd(b, a % b);
}

求出第n个丑数，可以使用二分法中的左开右开方式来做。

左边界l = 0，右边界r = min(a, min(b, c)) * n + 1

class Solution {
    public int nthUglyNumber(int n, int a, int b, int c) {
        long lcm_ab = lcm(a, b);
        long lcm_bc = lcm(b, c);
        long lcm_ac = lcm(a, c);
        long lcm_abc = lcm(a, lcm(b, c));
        int min = min(a, min(b, c));
        long l = 1, r = min * 1L * n ;
        while (l  < r) {
            long m = l + (r - l) / 2;
            long count = m / a + m / b + m / c - m / lcm_ab - m / lcm_ac - m / lcm_bc + m / lcm_abc;
            if (count < n) {
                l = m+1;
            } else {
                r = m;
            }
        }
        return (int) r;
    }

    private int min(int a, int b) {
        return Math.min(a, b);
    }

    // 求最小公倍数
    private long lcm(long a, long b) {
        return a * 1L * (b / gcd(a, b));
    }

    // 求最大公约数
    private long gcd(long a, long b) {
        return b == 0 ? a : gcd(b, a % b);
    }
}

补充理解：

根据丑数的定义:丑数是可以被a或 b 或 c 整除的 正整数,

所以丑数是a或 b 或 c的某一倍数.

假设只有一个数a = 2,第四个丑数就是 a * 4 即2 * 4 = 8,

假设有a = 2, b = 3两个数的情况下 对于12是第几个丑数呢?,很容易推出是 12 // 2 + 12 // 3 - a和b公共的部分,

对于公共部分的丑数则是6和12 而6和12是a, b的最小公倍数6的倍数,

那么对于a = 2, b = 3, c = 4三个数的情况,12则是第12 // 2 + 12 // 3 + 12 // 4 - a和b公共的部分- a和c公共的部分- b和c公共的部分+ a, b, c公共的部分，为什么要+ a, b, c公共的部分,因为对于12 它是2,3,4最小公倍数,同时也是其中任意两的最小公倍数的倍数,相当于之前减的时候多减了一次,因此要加回去.