games101【lecture13-16】Ray Tracing—辐射度量学

Basic radiometry (辐射度量学)

学习思路：为甚要学？学的是什么？它是怎样做的

提出动机

1. Blinn-Phong model 存在一定的问题——光的一些强度之类精确定义

定义及作用

1. 如何去描述光照
2. 定义了光的属性：
   • Radiant flux
   • intensity
   • irradiance
   • radiance

Radiant Energy and Flux (Power)

lm = lumen 表示灯泡有多亮

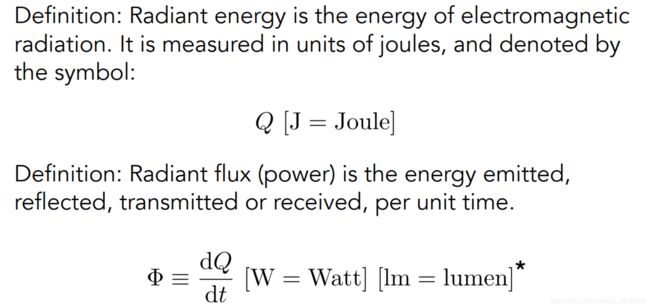
或者说flux为一个感光元件，单位时间内感受到的光。

光的衡量

1. Radiant Intensity ：任何一个物体散发的能量
2. Irradiance：物体表面接收到的能量
3. Radiance：光线传播过程中的能量
   

Radiant Intensity

定义

The radiant (luminous) intensity is the power per unit solid angle emitted by a point light source. （立体角上的能量）

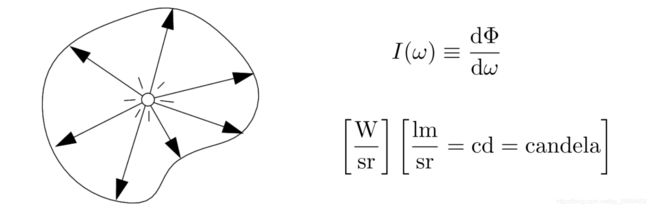
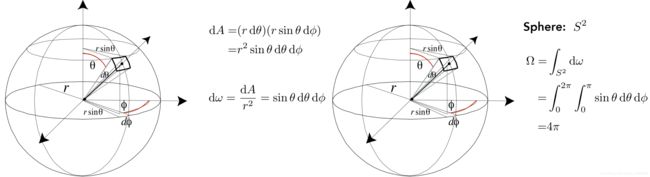
立体角的探讨

1. 2D：对于一个θ角，其等于l/r，也就是弧长和半径的比值，总的角度为2Π
2. 3D：推广到三维则有Ω= A/(r的平方)，也就是
3. 因此其立体角则可根据如下计算得到，θ为球体在z轴的夹角，Φ为x轴的夹角
   

Irradiance

**定义：**The irradiance is the power per unit area incident on a surface point. （**光线投射垂直到接受面的面积，类比与之前的Lambert’s Cosine Law **）

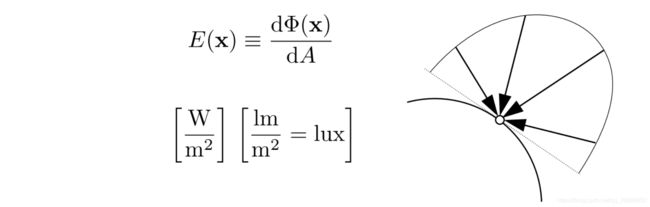
已知irradiance是单位面积上能量，那么可以看作如下方式计算：从半径为1，和半径为r上去计算点光源圆周单位面积的能量。实际上并不是光的intensity在衰减，而是随着距离增加，其irradiance在衰减。

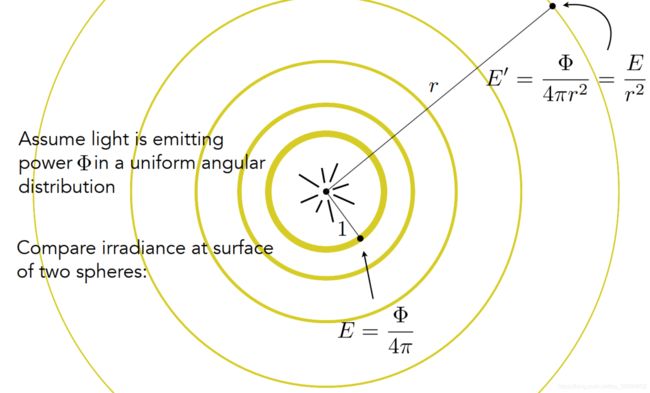
Radiance

The radiance (luminance) is the power emitted, reflected, transmitted or received by a surface, per unit solid angle, per projected unit area (就是单位面积上的单位立体角的辐射出能量)

在之前已经有如下定义：

1. Irradiance: power per projected unit area
2. Intensity: power per solid angle

那么可以知道：

1. Radiance: Irradiance per solid angle
2. Radiance: Intensity per projected unit area

Irradiance vs. Radiance

个人理解：

前者是一个单位面积接收的所有进来光线的能量，那么将所有进来的光线能量看成是不同方向单位立体角的积分的话，就可以理解到后者其实就是前者的在单位立体角上的能量（但是如果是放到单位立体角来说的话，前者和后者仅仅存在方向上的正负）。

同样的，对比Radiance和Intensity，则可知道后者是点光源往周围辐射的能量（假设点光源是均匀往周围辐射），那么前者就是在圆周上某一个单位面积所获得的能量。

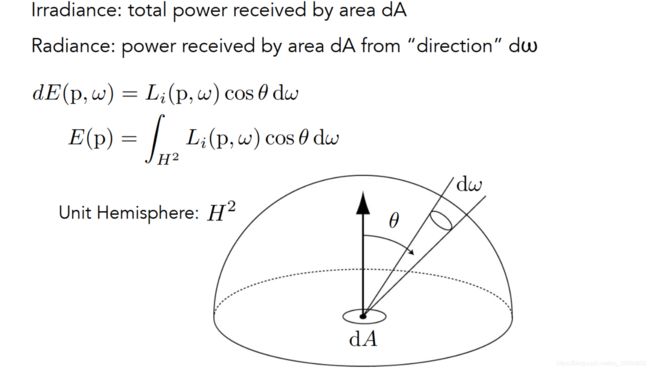
1. dE() ：irradiance
2. Li() ：radiance

BRDF —双向反射分布函数

定义：一束光进来，打到一个点上，如何往四面八方反射

从辐射度量学上来说，就是单位面积接收到的特定角度的irradiance，如何往各个方向发出radiance

事实上，这样反射光线的方法，同时也可以去定义物体的材质

反射方程

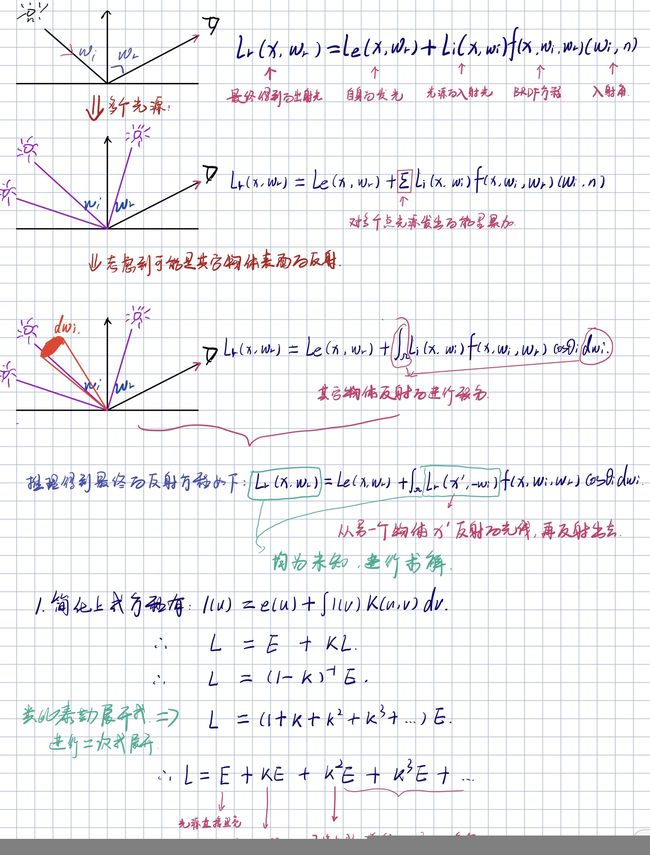
那么可以得到其反射方程：任何一个着色点，在各种不同光的照射下，所有入射方向的光线对反射出去特定角度（比如相机方向）的贡献。

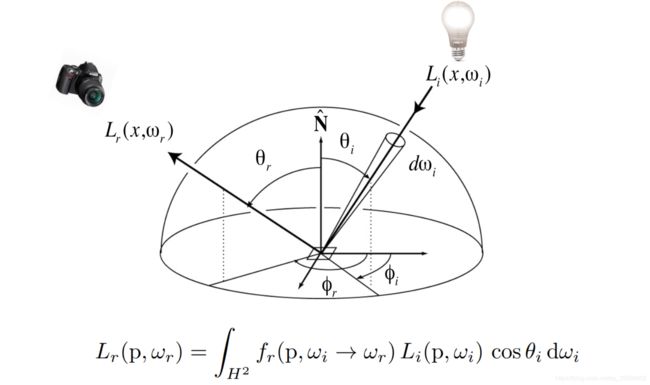
渲染方程

还需考虑到入射光线是否为其它多次弹射光线的集合等等，那么有如下定义：

1. 若只考虑光线一次弹射，则上图中Li为光源
2. 光线弹射多次，则Li还包括很多光源

方程通用化

还需考虑到物体本身的发光项，那么可以得到如下方程表达

其中Le为发光项，Ω定义为半球，这是因为下半球往上辐射的光可以进行忽略。

论文引用一下：[1]Kajiya, James T . The rendering equation[J]. Acm Computer Graphics, 1986, 20(4):143-150.

公式推理

直接光照：光线弹射0次

间接光照：光线弹射很多次

全局光照：直接光照和间接光照的集合

光栅化部分：弹射零次和一次的效果

全局光照解

概率论

随机变量：取的一些值

随机变量分布：就是取值的不同的概率集合

随机变量和概率的关系：如摇色子，它的取123456的概率总和为1，且每个值概率均等。

期望：

Probability Distribution Function (PDF) —概率密度函数

1. 概率密度函数的曲线下面积为概率，比如x取-2~-1，则在此区间它的概率为该区间的曲线下面积。
2. 该函数下面总和为1
   3. 如果需要考虑一个随机变量函数的期望计算？
   • Y = f(x)
   • E[Y] = E[f(X)] = 将上图中期望计算公式中的x替换为f(x)

Monte Carlo Integration（蒙特卡洛积分）

为什么使用？——用于解决定积分，在函数非常复杂的情况下，将其数值化计算，这样就不需要去解析出函数方程

具体内容：——采样多次不同长方形的大小面积，再平均去逼近曲线下面积（积分域不断采样，然后得到宽高，计算长方形面积后，采样多次求平均得到结果）

公式：

更通用的解释：采样f(x)得到的点，然后将该点除以其概率密度函数上的对应解，采样多次求平均

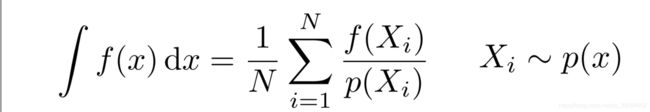
path tracing

可以做到真实照片级渲染

Whitted-Style Ray Tracing

1. 表现在镜面反射上
2. 在漫反射则会停止光线弹射

*存在问题：

1. 在Utah tespot上，如果是做出glossy的效果的话，还是会往高光设置，这样不对的。
   
2. 空间中应该会存在全局光照现象，并且随着光在材质上的反射会造成光随着材质颜色不同而反射出对应的颜色（color bleeding）
   

解决方法——计算直接光照

1. 使用上述的BRDF用于解全局光照
2. 那么就需要求解积分
3. 递归计算

举例计算

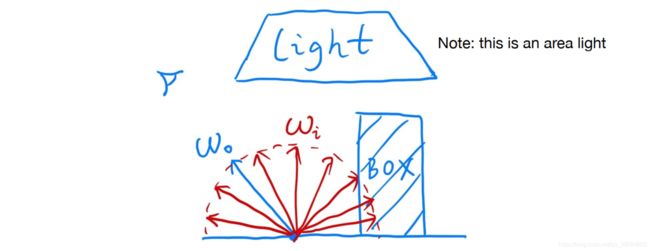
1. 设场景内存在一个点光源、一个平面光照和一个BOX，计算其全局光照

2. 设Wi为该点周围光线的入射角度，但是假设方向都是点出射出去的光线，即向外
   

3. 计算得到点光源的反射函数

   • 基于蒙塔卡罗积分进行积分求解
   • f(x)为反射函数中的函数
   • pdf：概率密度分布为半个球面，那么假设均匀采样的话，就为1/2Π
     
     解得方程如下：分母为pdf计算
     
     算法：

4. 直接光照计算

//着色p
shade(p, wo)
	// N个方向进行采样
	Randomly choose N directions wi~pdf
	Lo = 0.0
	// 任何方向计算
	For each wi
		// 追踪光线
		Trace a ray r(p, wi)
		// 如果光线打到了光源
		If ray r hit the light
			Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
	Return Lo

2. 全局光照计算
   • 当相机光线达到物体A上，然后物体还会进行弹射到另外一个物体B，再反射到光源（举例二次反射）
   • 那么其实可以将二次反射的光线，看作从A出发的光，打到B，然后进入光源

//着色p
shade(p, wo)
	// N个方向进行采样
	Randomly choose N directions wi~pdf
	Lo = 0.0
	// 任何方向计算
	For each wi
		// 追踪光线打到p点
		Trace a ray r(p, wi)
		// 如果p点出发的光线打到了光源
		If ray r hit the light
			Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
        // 增加判断是否打到物体
        Else If ray r hit an object at q
        	Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi)
	Return Lo

存在问题

1. 上述方式会导致光线数量爆炸，因为射出的光线假设达到100万个，然后如果均打到物体上，就需要迭代，那么就是指数幂增长
2. 如何解决？——当点发出光线数量为N的时候，指数增长也不变
3. 修改算法（当N等于1才叫路径追踪算法，大于1则是分布式光线追踪）：

//着色p
shade(p, wo)
	// 1个方向进行采样
	Randomly choose ONE directions wi~pdf(w)
    // 追踪光线打到p点
    Trace a ray r(p, wi)
    // 如果p点出发的光线打到了光源
    If ray r hit the light
    	return L_i * f_r * cosine / pdf(wi)
    // 增加判断是否打到物体
    Else If ray r hit an object at q
    	return shade(q, -wi) * f_r * cosine / pdf(wi)

算法内容

就是从相机出发，计算穿过每个像素的多条路线

伪代码：射线产生

ray_generation(camPos, pixel)
	// 在像素点上采样N点
	Uniformly choose N sample positions within the pixel
	pixel_radiance = 0.0
	For each sample in the pixel
		// 对任何选取的位置，从视点连接到样本，形成射线
		Shoot a ray r(camPos, cam_to_sample)
		// 如果r打到场景中点p
		If ray r hit the scene at p
			// 对p点到相机进行着色求平均
			pixel_radiance += 1 / N * shade(p, sample_to_cam)
	Return pixel_radiance

但是上述shade算法存在问题就是递归如何停止？——俄罗斯轮盘赌

Russian Roulette (RR) ——俄罗斯轮盘赌

在左轮手枪中装n枚子弹，弹夹容量为k，那么生存概率就是(k-n) / k

那么有如下算法使得，在停掉shading的时候，还能得到Lo

1. 随机设置一个概率P（0
2. 以一定的概率P射出光线，得到一定的结果后，使得Lo / P
3. 那么以1-P，不射光线，则得到0
4. 那么就有：期望E=P*(Lo / P) + (1-P)*0 = Lo

shade(p, wo)
	// 设定概率值
	Manually specify a probability P_RR
	// 随机生成光线的概率
	Randomly select ksi in a uniform dist. in [0, 1]
	// 如果概率小于设定值，则返回0
	If (ksi > P_RR) return 0.0;
	// 射出一条光线
	Randomly choose ONE direction wi~pdf(w)
	Trace a ray r(p, wi)
	If ray r hit the light
		// 返回乘上期望值的数
		Return L_i * f_r * cosine / pdf(wi) / P_RR
	Else If ray r hit an object at q
		Return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR

上述为正确的光线追踪，但是会使得不怎么高效

出现以下情况：

改进——针对光源采样

设当平面光足够大，像素点只要射出5条光线即可达到光源，而当平面光源很小的时候，有可能射出50000条射线都无法打到光源。那么是否可以从光源出发进行采样？

可以

1. 设光源pdf = 1 / A (because ∫pdf dA = 1)

2. 渲染方程在立体角：Lo = ∫Li fr cos dω

3. 但是在渲染方程中是对物体的dw积分，可以通过角度转换得到光源的单位面积和物体单位面积的关系如下：

   • 使用dAcosθ的原因是因为它要转为物体表面单位面积，该单位面积垂直于射线w,那么就可以推理得到最终的转化关系
     

4. 那么可以得到最后的反射方程为：
   

5. 上述改进是在计算直接光照的时候，计算得出，那么其着色方程可以分为直接光照和间接光照计算

shade(p, wo)
	# Contribution from the light source.
	Uniformly sample the light at x’ (pdf_light = 1 / A)
	L_dir = L_i * f_r * cos θ * cos θ’ / |x’ - p|^2 / pdf_light
	
	# Contribution from other reflectors.
	L_indir = 0.0
	Test Russian Roulette with probability P_RR
	Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi)
	Trace a ray r(p, wi)
	If ray r hit a non-emitting object at q
		L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR
	Return L_dir + L_indir

点光源处理

推荐设置为很小的面积光源，然后使用path tracing

Ray tracing方法介绍

1. (Unidirectional & bidirectional) path tracing
2. Photon mapping
3. Metropolis light transport
4. VCM / UPBP 等等

如何使得采样方向均匀分布在采样表面

选择什么样的PDF会更好

随机数如何分布均匀——low discrepancy sequences