插值拟合模型 之 Hermite插值、三次样条插值
常常需要根据已知的函数点进行数据、模型的处理和分析，而有时候现有的数据是极少的，不足以支撑分析的进行，这时就需要使用一些数学的方法，“模拟产生”一些新的但又比较靠谱的值来满足需求，这就是插值的作用。（也可以用于短期预测，反正样本点不能太多）
定义与概念
注：建模比赛中前两种用得比较多
插值法 原理以及证明过程如下（了解原理后可跳过）
以下介绍两种简单插值方法，但是效果一般不太理想，特别是对于容量较大的数据集。
（1）拉格朗日插值法
在数值分析中，拉格朗日插值法是以法国十八世纪数学家约瑟夫∙路易斯∙拉格朗日命名的一种多项式插值方法。在若干个不同的地方得到相应的观测值，拉格朗日插值法可以找到一个多项式，其恰好在各个观测的点取到观测到的值。
以三个点为例：
（2）牛顿插值法
两种插值方法单的对比
两种插值方法缺点
（1）上面讲的两种插值仅仅要求插值多项式在插值节点处与被插函数有相等的函数值，而这种插值多项式却不能全面反映被插值函数的性态。然而在许多实际问题中，不仅要求插值函数与被插值函数在所有节点处有相同的函数值，它也需要在一个或全部节点上插值多项式与被插函数有相同的低阶甚至高阶的导数值*。对于这些情况，拉格朗日插值和牛顿插值都不能满足
（2）龙格现象
高次插值会产生龙格现象，即在两端处波动极大,产生明显的震荡。在不熟悉曲线运动趋势的前提下，不要轻易使用高次插值。（次数高精度未必提高，而且摄入误差可能显著增大）
解决方式：分段低次插值（就是每几个点计算一次插值函数，然后构成一个分段函数）。
下面我们以每三个点插值一个二次函数为例（分段二次插值）
这个思想来源于牛顿插值法的（虽然牛顿插值法也没有很好地解决）
下面我们介绍两种数模中常用的插值算法，可以运用在建模中
一、埃尔米特(Hermite)插值
不但要求在节点上的函数值相等，而且还要求对应的导数值也相等,甚至要求高阶导数也相等，满足这种要求的插值多项式就是埃尔米特插值多项式。
原理
直接使用Hermite插值得到的多项式次数较高，也存在着龙格现象，因此在实际应用中，往往使用分段三次 Hermite 插值多项式 (PCHIP)。
Matlab有内置的函数（实现过程已经帮我们封装好了，会调用就行了）：
p = pchip(x,y, new_x)
% x是已知的样本点的横坐标;
% y是已知的样本点的纵坐标;
% new_x是要插入处对应的横坐标
二、三次样条插值
这种插值方法相对于Hermite对条件要求更加苛刻，但是所得到的曲线也更为光滑
Matlab也有内置的函数：
p = spline (x,y, new_x)
% x是已知的样本点的横坐标;
% y是已知的样本点的纵坐标;
% new_x是要插入处对应的横坐标
两种插值的具体内容以及推导过程参考《现代数值计算方法》（用得到再看吧，反正我没看懂）
两种插值方法对sin(x)插值对比图如下：
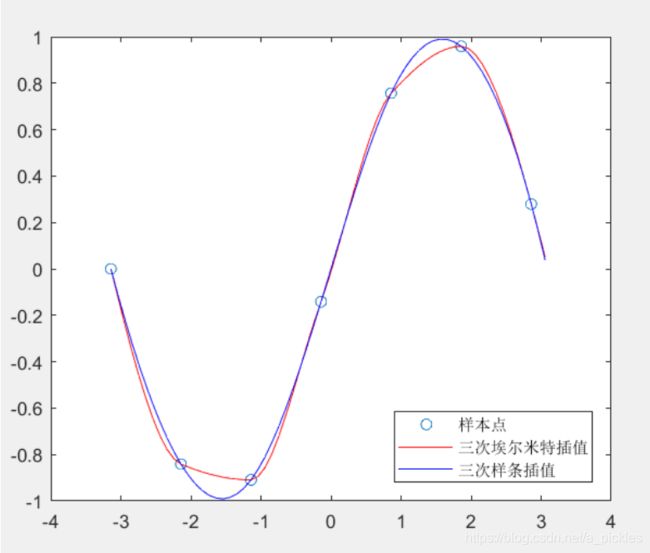
n维数据插值
p = interpn(x1,x2,...,xn, y, new_x1,new_x2,...,new_xn, method)
% x1,x2,...,xn是已知的样本点的横坐标
% y是已知的样本点的纵坐标坐标
% new_x1,new_x2,...,new_xn是要插入点的横坐标
% method是要插值的方法
% ‘linear’：线性插值（默认算法）；
% ‘cubic’：三次插值；
% ‘spline’：三次样条插值法；(最为精准) ‘nearest’：最邻近插值算法。
数据只有一维时与上面方法结果相同
x = ‐pi:pi; y = sin(x);
new_x = ‐pi:0.1:pi;
p = spline(x, y, new_x);
% 等价于 p = interpn (x, y, new_x, ’spline’);
plot(x, y, 'o', new_x, p, 'r‐')