2022.10.10 第三次周报
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、线性回归
-
- 一元线性回归
- 多元线性回归 梯度下降
- 二、神经网络-浅学习
-
- 数学基础
- 神经网络基础
-
- 完整的神经网络需要掌握的知识
- softmax函数
- 总结
前言
这周前期安装了jupyter notebook,并且学习了如何使用这个编译器,同时一边学一边手推了一元线性回归和多元线性回归(简单的梯度下降)。
一、线性回归
为了弄懂梯度下降的过程,决定手推一边线性回归,但这是一个特征向量的,多个特征向量的过程太过于复杂。


一元线性回归
import numpy as np
x = np.random.randint(0,10,10)
print (x )
noise = np.random.normal(0,3,10)
y=x*5+6+noise
print(y)
以上是设置原始的y和x
w = ((x*y).mean()-x.mean()*y.mean())/((x**2).mean()-x.mean()**2)
b = y.mean()-w*x.mean()
以上是寻找斜率w和截距b
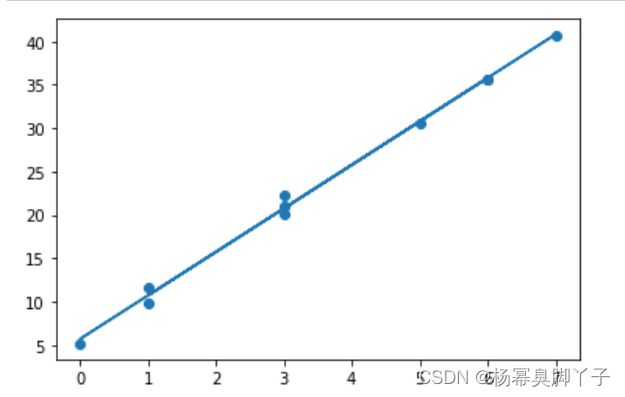
import matplotlib.pyplot as plt
y_h = w*x+b
plt.scatter(x,y)
plt.plot(x,y_h)
plt.show()
多元线性回归 梯度下降
import numpy as np
X = np.random.normal(10,1,100) #正态分布,10附近,1标准差,100个
X = np.reshape(X,(20,5)) #把100个数分为20份,5个向量一组
noise = np.random.normal(0,1,20) #加入噪声,0附近,1标准差,20个
y = np.dot(X,[6,4,5,3,2])+2+noise #在W为[6,4,5,3,2]基础上求出原来的y
y = np.reshape(y,(20,1)) #把y进行换成20*1的矩阵,方便后面进行点积(内积)
print (y)
以上代码是生成原始的数据
def Regression(X,y,alpha = 0.001,learning_count = 10000): #封装成函数
#alpha = 0.01 #学习率
#learning_count = 10000 #学习次数
W = np.zeros(shape=[1,X.shape[1]]) #设置W为[0,0,0,0,0]的向量
b = 0 #截距为0
for i in range (1000): #开始循环学习
y_h = np.dot(X,W.T) + b #求新的y
lost = y_h - y #代价函数
W = W - alpha*(1/len(X))*np.dot(lost.T,X)
b = b - alpha*(1/len(X))*lost.sum()
return W,b
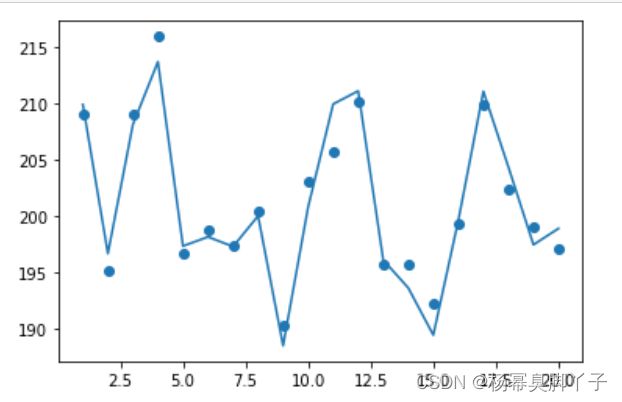
在多次迭代之后,找出最合适的w和b,并且封装起来;公式是和视频学的,其推导过程和一元的差不多就不做了。
W,b = Regression (X,y)
y_pre = np.dot(X,W.T)+b
print(y_pre)
二、神经网络-浅学习
来源:1.神经网络基础
数学基础
一次函数:y=kx+b ;在神经网络中神经单元的加权输入可以表示为一次函数关系,在反向传播算法中,一次函数可以使得计算变得十分简单。在神经网络中神经元的加权输入可以表示成多个自变量的一次函数形式,z=wx1+wx2+b,其中z为输入,w为权重,b为偏置。
sigmoid函数:sigmoid函数是神经网络中十分重要的激活函数,表达式为:
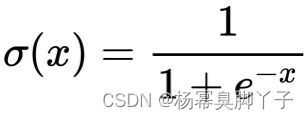
是光滑的曲线,处处可导。
倒数基础,复合函数求导,在反向传播算法中复合函数求导十分重要。在反向传播中会用到链式法则,包括单变量和变量函数的链式法则。
矩阵的四则运算。
矩阵的导数(没学–9.30)
计算图,计算图可以看作是描述function的语言,是一种将计算形式化的方法。包括正向传播和反向传播(梯度法则,通过偏导数求梯度)

假设求x和z的梯度。
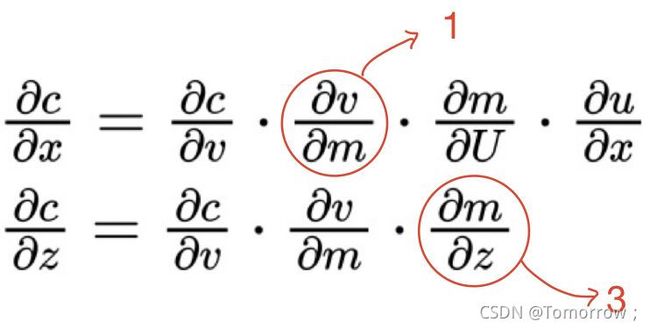
神经网络基础
1.神经元和神经网络结构:

一层输入层,n层隐藏层,一层输出层,它接收若干输入并执行加权求和以产生输出。它的输入是一个向量,输出是一个标量。
神经网络又称为多层感知机,由多个感知机相互连接从而形成隐藏层,隐藏层是构成非线性的基础,将输入层映射到输出层,也称之为ANN。ANN是输入到输出的映射,该映射通过带偏差的输入加权来计算。
完整的神经网络需要掌握的知识
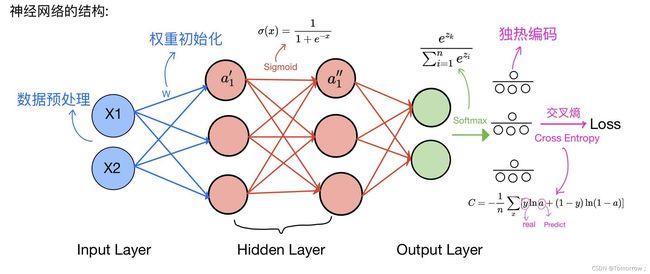
数据预处理:对拿到是数据进行再次整理,避免太多噪声影响数据的真实性,可以提高提升训练速度和提高模型精度,常用的方法有归一化。
权重初始化:不能简单设置为0,因为b为常数,在反向推到的时候,求偏导数时,使得全部梯度都相同了,所以需要对权重进行高斯随机初始化,初始化成一个相对较小的值。
激活函数:常用的激活函数包括sigmoid函数,tanh函数,Relu函数。引入非线性的激活函数,可以使得输出可以逼近任意函数,从而更加准确的拟合数据集。
sigmoid函数:
import math
import numpy as np
y_sigmoid=1/(1+(np.exp(-W)))
softmax层:对神经网络的输出结果进行了一次换算,多与One-Hot编码一起使用,可以理解为对结果进行归一化,将输出结果以概率的形式展现出来。
One-Hot编码:又称为一位有效编码,主要是采用N位状态寄存器来对N个状态进行编码,每个状态都有他独立的寄存器位,并且在任意时候只有一位有效。
损失函数:分为分类问题和回归问题的损失函数。
过拟合:过拟合是指为了得到一致假设而使假设变得过度严格。避免过拟合是分类器设计中的一个核心任务。
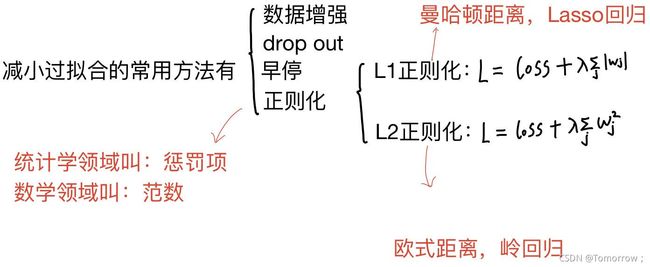 正则化后 Loss=损失项+正则化项。其中损失项用来衡量模型的拟合度,正则化项用来衡量模型的复杂度。
正则化后 Loss=损失项+正则化项。其中损失项用来衡量模型的拟合度,正则化项用来衡量模型的复杂度。
分类问题与回归问题的区别:
分类问题:输出是离散型变量,常用的模型有:逻辑回归,随即森林,多层感知机,朴素贝叶斯
回归问题:输出是连续型变量,常用的模型有:线性回归
softmax函数
参考:softmax的推理过程

softmax函数是一个分类问题里用到的函数,实际上是有限项离散概率分布的梯度对数归一化。以下是归一化指数函数代码实现示例,输入向量 [1,2,3,4,1,2,3]对应的Softmax函数的值为[0.024,0.064,0.175,0.475,0.024,0.064,0.175]。输出向量中拥有最大权重的项对应着输入向量中的最大值“4”。这也显示了这个函数通常的意义:对向量进行归一化,凸显其中最大的值并抑制远低于最大值的其他分量。
import math
z = [1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0]
z_exp = [math.exp(i) for i in z]
print(z_exp) # Result: [2.72, 7.39, 20.09, 54.6, 2.72, 7.39, 20.09]
sum_z_exp = sum(z_exp)
print(sum_z_exp) # Result: 114.98
# Result: [0.024, 0.064, 0.175, 0.475, 0.024, 0.064, 0.175]
softmax = [round(i / sum_z_exp, 3) for i in z_exp]
print(softmax)
总结
本周学习了一个和多个变量的线性回归方程,和基础的神经网络结构,进度比较慢。