构建数字高程模型的算法——不规则三角网(TIN, Triangulated Irregular Network)
构建数字高程模型的算法——不规则三角网(TIN, Triangulated Irregular Network)
文章目录
- 1.什么是数字高程模型?
- 2.为什么要构建数字高程模型?
- 3.如何构建数字高程模型?有几种方式?
- 4.DEM内插方法有哪些?
- 5.什么是移动曲面拟合法?
- 6.规则网络结构和不规则三角网是什么?
- 7.规则格网和不规则三角网各自优缺点?
- 8.什么是三角剖分(Triangulation)?
- 9.TIN与狄洛尼三角网的区别?
- 10.什么是Delaunay 剖分方法?
- 11.TIN特点?
- 12.Delaunay三角网的特点?
- 13.Delaunay三角网的应用?
- 14.TIN的基本元素?
- 15.TIN的体系结构?
- 16.TIN原始数据类型?
- 17.三角剖分算法有哪些?
- 18.Delaunay三角网基本算法有哪些?
- 19.Delaunay三角网基本算法的不足之处?
- 20.凸闭包生成算法的步骤包括哪几步?
- 21.规则数据生成三角网?
1.什么是数字高程模型?
数字高程模型(Digital Elevation Model,DEM),是通过有限的地形高程数据实现对地面地形的数字化模拟(即地形表面形态的数字化表达),它是用一组有序数值阵列形式表示地面高程的一种实体地面模型,是数字地形模型(Digital Terrain Model,DTM)的一个分支,其它各种地形特征值均可由此派生。
来自:数字高程模型
地球表面高低起伏,呈现一种连续变化的曲面,这种曲面无法用平面地图来确切表示。于是我们就利用一种全新的数字地球表面的方法—— 数字高程模型 的方法,这种方法已被普遍广泛采用。数字高程模型即DEM(Digital Elevation Model),是以数字形式按一定结构组织在一起,表示实际地形特征空间分布的模型,也是地形形状大小和起伏的数字描述。
来自: 不规则三角网(TIN)
数字高程模型是利用有限的高程数据实现对地球表面的数字化模拟。
来自:高精度DEM建模的加权径向基函数插值方法

[1] Chen C F, Yue T X, Li Y Y. A High Speed Method of SMTS[J]. Computers and Geosciences,
2012, 41: 64-71.
[2] Chen C F, Fan Z M, Yue T X, et al. A Robust Estimator for The Accuracy Assessment of remote-sensing-derived DEMs[J]. International Journal of Remote Sensing, 2012, 33(8): 2482-2497.
2.为什么要构建数字高程模型?
由于DEM描述的是地面高程信息,它在测绘、水文、气象、地貌、地质、土壤、工程建设、 通讯、军事等国民经济和国防建设以及人文和自然科学领域有着广泛的应用。如在工程建设上,可用于如土方量计算、通视分析等;在防洪减灾方面,DEM是进行水文分析如汇水区分析、水系网络分析、降雨分析、蓄洪计算、淹没分析等的基础; 在无线通讯上,可用于蜂窝电话的基站分析等等。
来自:数字高程模型
3.如何构建数字高程模型?有几种方式?
建立DEM的方法有多种。从数据源及采集方式讲有:
(1)直接从地面测量,所涉及的仪器有水平导轨、测针、测针架和相对高程测量板等构件,也可以用GPS、全站仪 、野外测量等高端仪器;
(2)根据航空或航天影像,通过摄影测量途径获取,如立体坐标仪观测及空三加密法、解析测图、数字摄影测量等等;
(3)从现有地形图上采集,如格网读点法、数字化仪手扶跟踪及扫描仪半自动采集然后通过内插生成DEM等方法。
来自:建立DEM的方法
4.DEM内插方法有哪些?
DEM内插方法很多,主要有整体内插 、分块内插和逐点内插三种。
(1)整体内插的拟合模型是由研究区内所有采样点的观测值建立的。
(2)分块内插是把参考空间分成若干大小相同的块,对各分块使用不同的函数。
(3)逐点内插是以待插点为中心,定义一个局部函数去拟合周围的数据点,数据点的范围随待插位置的变化而变化,因此又称移动拟合法。
5.什么是移动曲面拟合法?
移动拟合法是典型的单点移面内插方法。对每一个待定点取一个多项式曲面来拟合该点附近的地形表面。此时,取待定点作为平面坐标的原点,并以待定点为圆心,以r为半径的圆内诸数据点来定义函数的待定系数。移动曲面拟合法分为规则网格结构和不规则网格三角网两种算法。
来自:移动拟合法
拓展:移动曲面拟合法DEM内插
6.规则网络结构和不规则三角网是什么?
规则格网 (Grid) :将区域空间切分为规则的格网单元,每个格网单元对应一个数值。数学上可表示为矩阵,计算机实现中则是二维数组,每个格网单元的一个元素对应一个高程值。每一个网格(cell)具有唯一的行(row)和列(column)标识,给出某一格网中的x、y地理坐标,可以定位一个网格。 每一个网格都有一个表示其地理特征的值。
来自:GIS基础-DEM Grid规则格网结构
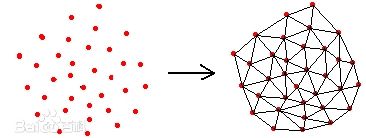
不规则三角网(Triangular Irregular Network, TIN):也名“曲面数据结构”,是由Peuker和他的同事于1978年设计的一个系统,它是根据区域的有限个点集将区域划分为相连的三角面网络,三角面的形状和大小取决于不规则分布的测点的密度和位置,能够避免地形平坦时的数据冗余,又能按地形特征点表示数字高程特征。最常用的生成方法是Delaunay 剖分方法。
来自:不规则三角网

7.规则格网和不规则三角网各自优缺点?
第一种表述:
| 优点 | 缺点 | |
|---|---|---|
| GRID | 能够充分表现高程变化的细节,拓扑关系简单,分析处理算法易于实现,某些空间操作及存储组织灵活方便 | 数据存储占用巨大的空间,并且在不规则的地形特征和较为平坦的地形特征之间在数据表示方面不够协调 |
| TIN | 高效率的存储,数据结构简单,与不规则的地面特征和谐一致,可以表示线性特征和迭加任意形状的区域边界,易于更新,可适应各种分布情况的数据 | 算法实现比较复杂和困难 |
来自:GIS基础-Grid与TIN比较
第二种表述:
在数字高程模型 (DEM) 中, Grid和TIN两种模型都是应用最广泛的连续表面数字表示的数据结构。
Grid优势:Grid作为规则格网的高程矩阵, 可以方便地用计算机进行处理, 特别是栅格数据结构的地理信息系统。它还可以很容易地计算等高线、坡度坡向、山坡阴影和自动提取流域地形等, 使得它成为DEM最广泛使用的格式。
Grid不足:在地形平坦的地方, 存在大量的数据冗余; 在不改变格网大小的情况下, 难以表达复杂地形的突变现象;在某些计算, 如通视问题, 过分强调网格的轴方向。
TIN优势:
TIN是另外一种表示数字高程模型的方法, 它即可以减少规则格网方法带来的数据冗余, 又能按地形特征点如山脊、山谷线、地形变化线等表示数字高程特征。
来自:一种有效的规则网格到不规则三角网的转换算法
(另一种说法)在计算 (如坡度) 效率方面优于纯粹基于等高线的方法。不规则三角网能随地形起伏变化的复杂性而改变采样点的密度和决定采样点的位置, 因而它能够避免地形起伏平坦时的数据冗余。
来自:VB环境下不规则三角网的算法设计与实现
TIN不足:TIN 模型的适用范围不及栅格表面模型那么广泛,且构建和处理所需的开销更大。获得优良源数据的成本可能会很高,并且,由于数据结构非常复杂,处理 TIN 的效率要比处理栅格数据低。
来自:不规则三角网(TIN)
第三种表述:
目前常用的算法是TIN,然后在TIN基础上通过线性和双线性内插建立DEM。用规则方格网高程数据记录地表起伏的优点有:(X,Y)位置信息可隐含,无需全部作为原始数据存储。由于是规则网高程数据,以后在数据处理方面比较容易。缺点有:数据采集较麻烦,因为网格点不是特征点,一些微地形可能没有记录。TIN结构数据的优点:能以不同层次的分辨率来描述地表形态。与格网数据模型相比,TIN模型在某一特定分辨率下能用更少的空间和时间更精确地表示更加复杂的表面.特别当地形包含有大量特征如断裂线、构造线时,TIN模型能更好地顾及这些特征。
来自:数字高程模型
拓展:线性插值和双线性插值

线性插值:在AB段计算斜率,Yc=Ya+(Xc-Xa)*(Yb-Ya)/(Xb-Xa)。

双线性插值:AB插值求E,CD插值求F,EF插值求G。
来自:直观理解线性插值(linear interpolation)和双线性插值(Bilinear interpolation)
8.什么是三角剖分(Triangulation)?
第一种表述:
三角剖分是代数拓扑学里最基本的研究方法。 以曲面为例, 我们把曲面剖开成一块块碎片,要求满足下面条件: (1)每块碎片都是曲边三角形; (2)曲面上任何两个这样的曲边三角形,要么不相交,要么恰好相交于一条公共边(不能同时交两条或两条以上的边)。
来自:三角剖分

第二种表述:
三角剖分:假设V是二维实数域上的有限点集,边e是由点集中的点作为端点构成的封闭线段, E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G,该平面图满足条件:
1.除了端点,平面图中的边不包含点集中的任何点。
2.没有相交边。
3.平面图中所有的面都是三角面,且所有三角面的合集是散点集V的凸包。
来自:Delaunay三角剖分算法
拓展:
在二维欧几里得空间中,凸包可想象为一条刚好包著所有点的橡皮圈。

第三种表述:
如何把一个散点集合剖分成不均匀的三角形网络,这就是散点集的三角剖分问题,散点集的三角剖分,对数值分析以及图形学来说,都是极为重要的一项预处理技术。
来自:3、表面建模
9.TIN与狄洛尼三角网的区别?
TIN是一系列不重叠连续的的三角网,狄洛尼三角网是按照狄洛尼原则生成的三角网。也就是说有很多种方法可以生成Tin,狄洛尼三角网只是其中一种生成结果。
来自:TIN与狄洛尼三角网的区别?
10.什么是Delaunay 剖分方法?
第一种表述:
Delaunay三角网: 由一系列相连的但不重叠的三角形的集合, 而且这些三角形的外接圆不包含这个面域的其他任何点。
总结一句话就是生成的三角网中的任意一个三角形不能包含其他的三角形的顶点。
来自:Delaunay三角网
第二种表述:
Delaunay三角剖分:如果点集V的一个三角剖分T只包含Delaunay边,那么该三角剖分称为Delaunay三角剖分。
Delaunay边:假设E中的一条边e(两个端点为a,b),e若满足下列条件,则称之为Delaunay边:存在一个圆经过a,b两点,圆内(注意是圆内,圆上最多三点共圆)不含点集V中任何其他的点,这一特性又称空圆特性。

来自:Delaunay三角剖分算法
拓展:
Dirichlet(1850年)和Voronoi(1908年)最早讨论空间散点的关系问题。
Voronioi图把平面分成N个区域,每一个区域包含一个点,该点所在的区域是距离该点最近的点的集合。
11.TIN特点?
T:三角化(Triangulated),是离散数据的三角形剖分过程,也是TIN的建立过程。位于三角形内的任意一点的高程值均可以通过三角形平面方程唯一确定。
I:不规则性(Irregular),指用来构建TIN的采样点的分布形式。TIN具有可分辨率,比格网DEM能更好的反应地形起伏。
N:网(Network),表达整个区域的三角形分布形态,即三角形之间不能交叉和重叠。三角形之间的拓扑关系隐含其中。
来自:第五章_不规则三角网(TIN)的建立
12.Delaunay三角网的特点?
第一种表述:


其中,空外接圆准则和张角最大准则是最常用的两种准则
来自:Delaunay三角网
第二种表述:
1.最接近:以最近的三点形成三角形,且各线段(三角形的边)皆不相交。
2.唯一性:不论从区域何处开始构建,最终都将得到一致的结果。
3.最优性:任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话,那么两个三角形六个内角中最小的角度不会变大。
4.最规则:如果将三角网中的每个三角形的最小角进行升序排列,则Delaunay三角网的排列得到的数值最大。
5.区域性:新增、删除、移动某一个顶点时只会影响临近的三角形。
6.具有凸多边形的外壳:三角网最外层的边界形成一个凸多边形的外壳。

来自:Delaunay三角剖分算法
第三种表述:
1.不存在四点共圆;
2.每个三角形对应一个Voronoi图顶点;
3.每个三角形边对应一个Voronoi图边;
3.每个结点对应一个Voronoi图区域;
4.Delaunay图的边界是一个凸壳;
5.三角网中三角形的最小角最大。
来自:第五章_不规则三角网(TIN)的建立
13.Delaunay三角网的应用?
在所有可能的三角网中,狄洛尼(Delaunay)三角网在地形拟合方面运用的较普遍,因此常被用于TIN的生成。在狄洛尼三角网中的每个三角形可视为一个平面,平面的几何特征完全由三个顶点的空间坐标值(x,y,z)所决定。存储的时候,每个三角形分别构成一个记录,每个记录包括:三角形标识码、该三角形的相邻三角形标识码、该三角形的顶点标识码等。顶点的空间坐标值则另外存储。
用途:
(1)利用这种相邻三角形信息,便于连续分布现象的顺序追踪和查询检索,例如对等高线的追踪;
(2)利用这种数据结构,可方便地进行地形分析,如坡度和坡向信息的提取,填挖方计算,阴影和地形通视分析,等高线自动生成和三维显示等。
来自:不规则三角网
14.TIN的基本元素?
节点(Node):是相邻三角形的公共顶点,也是用来构建TIN的采样数据;
边(Edge):指两个三角形的公共边界,是TIN不光滑性的具体体现。边同时还包括特征线、断裂线以及区域边界;
面(Face):由最近的三个节点组成的三角形面,是TIN描述地形表面的基本单元。TIN中的每一个三角形都描述了局部地形倾斜状态,具有唯一的坡度值。三角形在公共点和边上是无缝的,或者说三角形不能交叉和重叠。

15.TIN的体系结构?
16.TIN原始数据类型?
用来TIN进行构建的原始数据根据数据点之间的约束条件可分为无约束数据域和约束数据域两种类型。
无约束数据域:是指数据点之间不存在任何关系,即数据分布完全呈离散状态,数据点之间在物理上相互独立。
约束数据域:则是部分数据点之间存在着某种联系,这种联系一般通过线性特征来维护,如地形数据中的山脊线、山谷线上的点等。
17.三角剖分算法有哪些?
包括:不规则分布采样数据三角剖分(从离散点生成TIN)、规则分布采样数据三角剖分、从混合数据生成三角网、基于等高线采样数据三角剖分四种方法。
在目前所有的三角算法中,以Delaunay三角网的应用最为广泛。Delaunay三角网为相互邻接且互不重叠的三角形的集合,每一个三角形的外接圆内不包含其他的点。
18.Delaunay三角网基本算法有哪些?
包括分治算法、渐次插入算法、三角网生长算法,三种算法。
分治算法


渐次插入算法
19.Delaunay三角网基本算法的不足之处?
20.凸闭包生成算法的步骤包括哪几步?
来自:3、表面建模





















