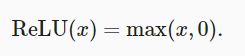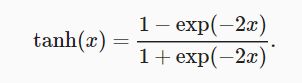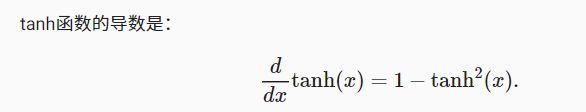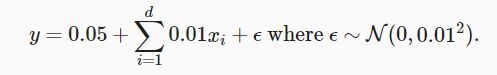深度学习系列笔记03多层感知机(上)
文章目录
- 1 感知机
- 2 多层感知机
-
- 2.1 在网络中加入隐藏层
- 2.2 非线性的变化
- 2.3 常用激活函数
-
- 2.3.1 ReLU函数
- 2.3.2 sigmoid函数
- 2.3.3 tanh函数
- 3 多层感知机的从零开始实现
-
- 3.1 初始化模型参数
- 3.2 激活函数
-
- zeros_like函数记录:
- 3.3 模型定义
- 3.4 损失函数
- 3.5 训练
- 4 多层感知机的简洁实现
- 5 模型选择、欠拟合和过拟合
-
- 5.1 训练误差和泛化误差
- 5.2 模型选择
-
- K 则交叉验证:
- 5.3 过拟合还是欠拟合
-
- 模型复杂度
- 数据集大小
- 5.4 多项式回归
-
- 5.4.1 生成数据集
- 5.4.2 对模型进行训练和测试
- 6 权重衰退
-
- 6.1 范数和权重衰退
-
- 总结:
- 6.2 从零开始实现
-
- 6.2.1 生成数据
-
- 函数记录:
- 6.2.2 初始化模型参数
- 6.2.3 定义L2范数惩罚
- 6.2.4 定义训练代码实现
- 6.3 简洁实现
-
-
- 函数记录:
-
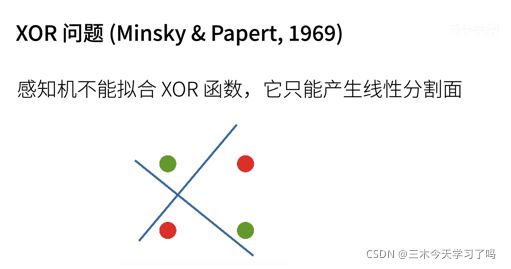
1 感知机
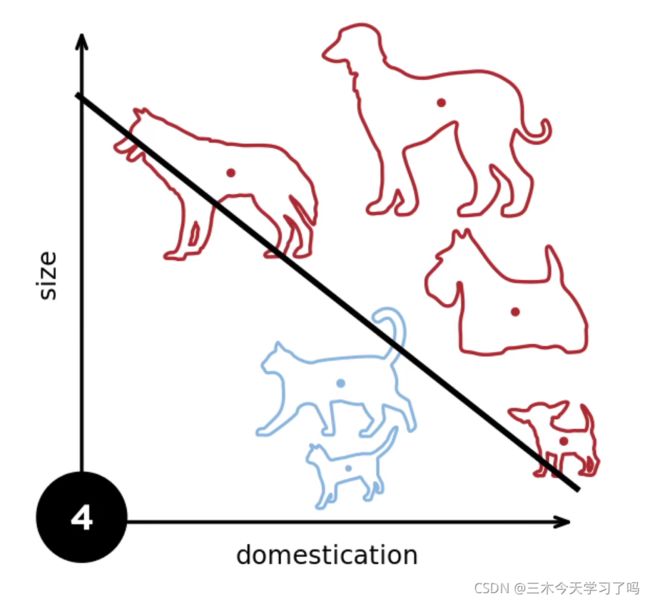
通过不断地引入数据点,使得这条直线可以有效地分割各种所有的训练数据。
2 多层感知机
回想一下softmax回归的模型结构。该模型通过单个仿射变换将我们的输入直接映射到输出,然后进行softmax操作。
如果我们的标签通过仿射变换后确实与我们的输入数据相关,那么这种方法就足够了。但是,仿射变换中的线性是一个很强的假设。
但对于很多标签而言,并不是简单的线性。
2.1 在网络中加入隐藏层
我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制,使其能处理更普遍的函数关系类型。
要做到这一点,最简单的方法是将许多全连接层堆叠在一起。每一层都输出到上面的层,直到生成最后的输出。
我们可以把前 L−1 层看作表示全连接层,把最后一层看作线性预测器。
该多层感知机有4个输入,3个输出,其隐藏层包含5个隐藏单元。输入层不涉及任何计算,因此使用此网络产生输出只需要实现隐藏层和输出层的计算;因此,这个多层感知机中的层数为2。
2.2 非线性的变化
2.3 常用激活函数
激活函数通过计算加权和并加上偏置来确定神经元是否应该被激活。它们是将输入信号转换为输出的可微运算。大多数激活函数都是非线性的
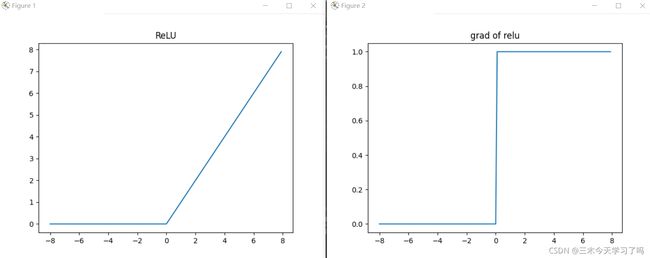
2.3.1 ReLU函数
import torch
import matplotlib.pyplot as plt
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
plt.figure(1)
plt.plot(x.detach(), y.detach())
plt.title('ReLU')
y.backward(torch.ones_like(x), retain_graph=True)
plt.figure(2)
plt.plot(x.detach(), x.grad)
plt.title('grad of relu')
plt.show() # 展示所有图片
当输入为负时,ReLU函数的导数为0,而当输入为正时,ReLU函数的导数为1。
使用ReLU的原因是,它求导表现得特别好:要么让参数消失,要么让参数通过。
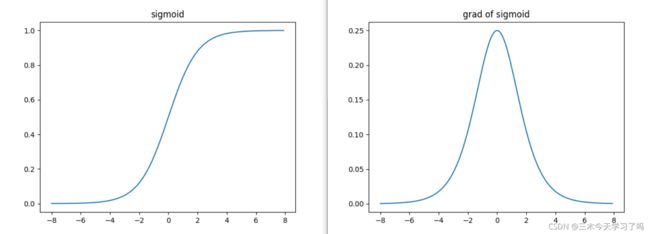
2.3.2 sigmoid函数
只需要修改一下y = torch.sigmoid(x)即可。
**sigmoid函数的导数:**当输入为0时,sigmoid函数的导数达到最大值0.25。而输入在任一方向上越远离0点,导数越接近0。
2.3.3 tanh函数
**tanh函数的导数:**当输入接近0时,tanh函数的导数接近最大值1。与我们在sigmoid函数图像中看到的类似,输入在任一方向上越远离0点,导数越接近0。
3 多层感知机的从零开始实现
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt
3.1 初始化模型参数
回想一下,Fashion-MNIST中的每个图像由 28×28=784 个灰度像素值组成。所有图像共分为10个类别。忽略像素之间的空间结构,我们可以将每个图像视为具有784个输入特征和10个类的简单分类数据集
通常,我们选择2的若干次幂作为层的宽度。因为内存在硬件中的分配和寻址方式,这么做往往可以在计算上更高效。
num_inputs, num_outputs, num_hiddens = 784, 10, 256 # 256是隐藏单元的个数
W1 = nn.Parameter(torch.randn(
num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]
3.2 激活函数
def relu(X):
a = torch.zeros_like(X)
return torch.max(X, a)
zeros_like函数记录:
a = torch.zeros_like(X) # 构造一个矩阵a,其维度与矩阵X一致
torch.max(X, a) # 使用最大值函数自己实现ReLU激活函数
3.3 模型定义
def net(X):
X = X.reshape((-1, num_inputs))
H = relu(X@W1 + b1) # 这里“@”代表矩阵乘法
return (H@W2 + b2)
3.4 损失函数
直接使用高级API中的内置函数来计算softmax和交叉熵损失。
loss = nn.CrossEntropyLoss()
3.5 训练
幸运的是,多层感知机的训练过程与softmax回归的训练过程完全相同。可以直接调用d2l包的train_ch3函数。
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
并且进行预测:
d2l.predict_ch3(net, test_iter)
4 多层感知机的简洁实现
与softmax回归的简洁实现(:numref:sec_softmax_concise)相比,唯一的区别是我们添加了2个全连接层(之前我们只添加了1个全连接层)。
![]()
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256), #从输入层到隐藏层
nn.ReLU(), # 从隐藏层到输出层
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
5 模型选择、欠拟合和过拟合
如何才能确定模型是真正发现了一种泛化的模式,而不是简单地记住了数据呢?
5.1 训练误差和泛化误差
训练误差(training error)是指,我们的模型在训练数据集上计算得到的误差。泛化误差(generalization error)是指,当我们将模型应用在同样从原始样本的分布中抽取的无限多的数据样本时,我们模型误差的期望。
我们永远不能准确地计算出泛化误差。这是因为无限多的数据样本是一个虚构的对象。在实际中,我们只能通过将模型应用于一个独立的测试集来估计泛化误差,该测试集由随机选取的、未曾在训练集中出现的数据样本构成。
5.2 模型选择
在机器学习中,我们通常在评估几个候选模型后选择最终的模型。这个过程叫做模型选择。
有时,需要进行比较的模型在本质上是完全不同的(比如,决策树与线性模型)。又有时,我们需要比较不同的超参数设置下的同一类模型。(例如,训练多层感知机模型时,我们可能希望比较具有不同数量的隐藏层、不同数量的隐藏单元以及不同的的激活函数组合的模型。)
理论上,我们使用训练数据训练模型,使用测试数据测试训练出来的模型。而且测试数据应该未出现在训练数据中,而且测试数据在使用一次后被丢弃。但我们很少能有充足的数据来对每一轮实验采用全新测试集。
解决此问题的常见做法是将我们的数据分成三份,除了训练和测试数据集之外,还增加一个验证数据集(validation dataset),也叫验证集(validation set)。 但现实是验证数据和测试数据之间的边界模糊得令人担忧。
K 则交叉验证:
当训练数据稀缺时,我们甚至可能无法提供足够的数据来构成一个合适的验证集。这个问题的一个流行的解决方案是采用 K 折交叉验证。这里,原始训练数据被分成 K 个不重叠的子集。然后执行 K 次模型训练和验证,每次在 K−1 个子集上进行训练,并在剩余的一个子集(在该轮中没有用于训练的子集)上进行验证。最后,通过对 K 次实验的结果取平均来估计训练和验证误差。
深度学习一般训练集合较大,所以K则交叉验证在深度学习中的训练成本太高了。
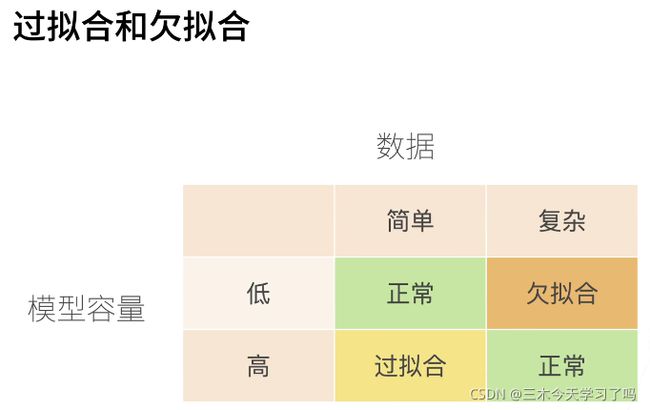
5.3 过拟合还是欠拟合
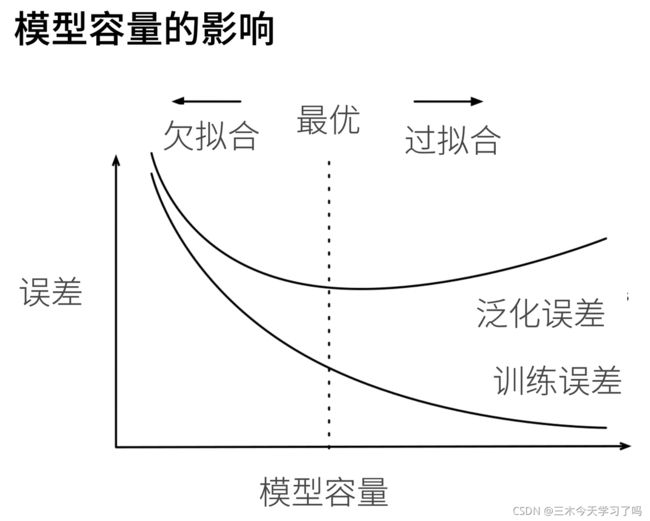
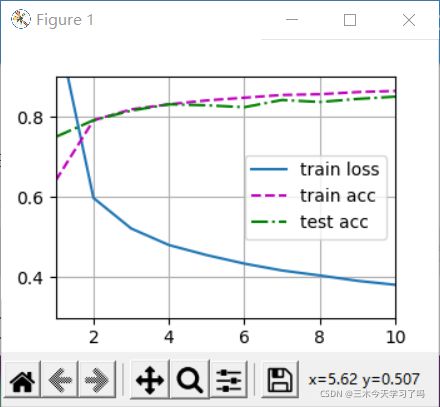
这个图很好理解。当我们的模型容量低的时候,模型既不能很好的拟合训练集,导致训练误差很大,同时模型的泛化能力也很差;当模型的容量很大时,显然可以拟合出测试集的所有数据,训练误差自然很小。但应对一个新的数据时,由于过拟合的原因,导致泛化误差很大。
是否过拟合或欠拟合可能取决于模型复杂性和可用训练数据集的大小。
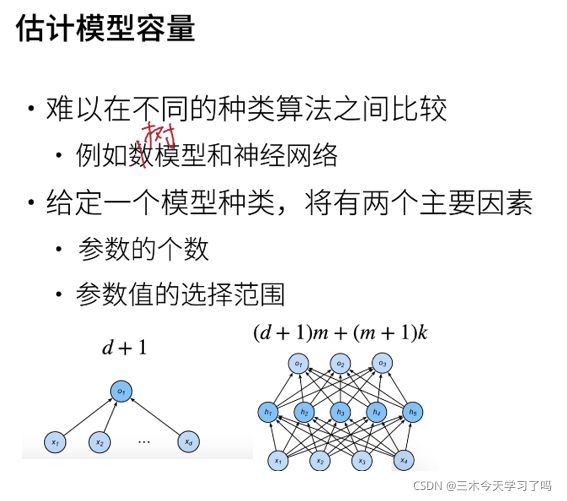
模型复杂度

高阶多项式函数比低阶多项式函数复杂得多。高阶多项式的参数较多,模型函数的选择范围较广。因此在固定训练数据集的情况下,高阶多项式函数相对于低阶多项式的训练误差应该始终更低。
数据集大小
训练数据集中的样本越少,我们就越有可能遇到过拟合。随着训练数据量的增加,泛化误差通常会减小。
模型复杂性和数据集大小之间通常存在关系。给出更多的数据,我们可能会尝试拟合一个更复杂的模型。
5.4 多项式回归
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt
5.4.1 生成数据集
max_degree = 20
n_train, n_test = 100, 100
true_w = np.zeros(max_degree) # [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
features = np.random.normal(size=(n_train + n_test, 1)) # (200, 1)
np.random.shuffle(features) # 打乱数据
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1)) # ((200, 1), (20, 1)) =(200, 20)
for i in range(max_degree):
poly_features[:, 1] /= math.gamma(i + 1)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)
# NumPy ndarray转换为tensor
true_w, features, poly_features, labels = [torch.tensor(x, dtype=
d2l.float32) for x in [true_w, features, poly_features, labels]]
print(features[:2], poly_features[:2, :], labels[:2])
函数笔记:
power(x1, x2), 对x1中的每个元素求x2次方。
gamma(n) = (n-1)!;
5.4.2 对模型进行训练和测试
实现一个函数来评估模型在给定数据集上的损失。
def evaluate_loss(net, data_iter, loss): # 导入数据和损失函数
"""评估给定数据集上模型的损失。"""
metric = d2l.Accumulator(2) # 损失的总和, 样本数量
for X, y in data_iter:
out = net(X)
y = y.reshape(out.shape)
l = loss(out, y)
metric.add(l.sum(), l.numel())
return metric[0] / metric[1]
现在定义训练函数。
def train(train_features, test_features, train_labels, test_labels,
num_epochs=400):
loss = nn.MSELoss()
input_shape = train_features.shape[-1]
# 不设置偏置,因为我们已经在多项式特征中实现了它
net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
batch_size = min(10, train_labels.shape[0])
train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),
batch_size)
test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),
batch_size, is_train=False)
trainer = torch.optim.SGD(net.parameters(), lr=0.01)
animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
xlim=[1, num_epochs], ylim=[1e-3, 1e2],
legend=['train', 'test'])
for epoch in range(num_epochs):
d2l.train_epoch_ch3(net, train_iter, loss, trainer)
if epoch == 0 or (epoch + 1) % 20 == 0:
animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
evaluate_loss(net, test_iter, loss)))
print('weight:', net[0].weight.data.numpy())
# 从多项式特征中选择前4个维度,即 1, x, x^2/2!, x^3/3!
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
labels[:n_train], labels[n_train:])
plt.show()
# 从多项式特征中选择前2个维度,即 1, x
train(poly_features[:n_train, :2], poly_features[n_train:, :2],
labels[:n_train], labels[n_train:])
高阶多项式函数拟合(过拟合)
# 从多项式特征中选取所有维度
train(poly_features[:n_train, :], poly_features[n_train:, :],
labels[:n_train], labels[n_train:], num_epochs=1500)
6 权重衰退
我们已经描述了过拟合的问题,现在我们可以介绍一些正则化模型的技术。
在多项式回归的例子中,我们可以通过调整拟合多项式的阶数来限制模型的容量。实际上,限制特征的数量是缓解过拟合的一种常用技术。 然而,简单地丢弃特征对于这项工作来说可能过于生硬。
6.1 范数和权重衰退
在训练参数化机器学习模型时, 权重衰减(通常称为 L2 正则化) 是最广泛使用的正则化的技术之一。
要保证权重向量比较小,最常用方法是将其范数作为惩罚项加到最小化损失的问题中
将原来的训练目标最小化训练标签上的预测损失,调整为最小化预测损失和惩罚项之和。
为了惩罚权重向量的大小,我们必须以某种方式在损失函数中添加 ∥w∥2 ,但是模型应该如何平衡这个新的额外惩罚的损失?实际上,我们通过正则化常数 λ 来描述这种权衡,这是一个非负超参数 。
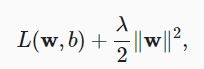
L2 正则化线性模型构成经典的岭回归(ridge regression)算法,L1正则化线性回归是统计学中类似的基本模型,通常被称为套索回归(lasso regression)。
 使用 L2 范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。
使用 L2 范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。
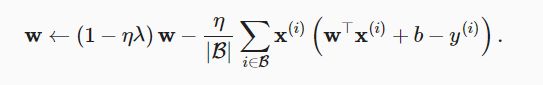
权重衰减为我们提供了一种连续的机制来调整函数的复杂度。较小的 λ 值对应较少约束的 w ,而较大的 λ 值对 w 的约束更大。
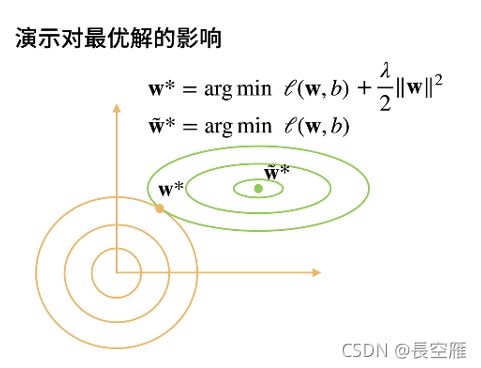
拉格朗日乘子法原本是用于解决约束条件下的多元函数极值问题。举例,求f(x,y)的最小值,但是有约束C(x,y) = 0。乘子法给的一般思路是,构造一个新的函数g(x,y,λ) = f(x,y) +λC(x,y),当同时满足gx = gy = 0(偏导)时,函数取到最小值。这件结论的几何含义是,当f(x,y)与C(x,y)的等高线相切时,取到最小值。
具体到机器学习这里,C(x,y) = w^2 -θ。所以视频中的黄色圆圈,代表不同θ下的约束条件。θ越小,则最终的parameter离原点越近。
总结:
L2正则化是在目标函数中直接加上一个正则项,直接修改了我们的优化目标。
权值衰减是在训练的每一步结束的时候,对网络中的参数值直接裁剪一定的比例,优化目标的式子是不变的。
要知道,避免过拟合的方法有很多:early stopping、数据集扩增(Data augmentation)、正则化(Regularization)包括L1、L2(L2 regularization也叫weight decay),dropout,不局限于权重衰退。
6.2 从零开始实现
6.2.1 生成数据
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)
函数记录:
synthetic_data(w, b, num_examples):
Generate y = Xw + b + noise.
6.2.2 初始化模型参数
def init_params():
w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]
6.2.3 定义L2范数惩罚
def l2_penalty(w):
return torch.sum(w.pow(2)) / 2
6.2.4 定义训练代码实现
def train(lambd):
w, b = init_params()
net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
num_epochs, lr = 100, 0.003
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
with torch.enable_grad():
# 增加了L2范数惩罚项,广播机制使l2_penalty(w)成为一个长度为`batch_size`的向量。
l = loss(net(X), y) + lambd * l2_penalty(w) # 总的loss
l.sum().backward()
d2l.sgd([w, b], lr, batch_size)
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数是:', torch.norm(w).item())
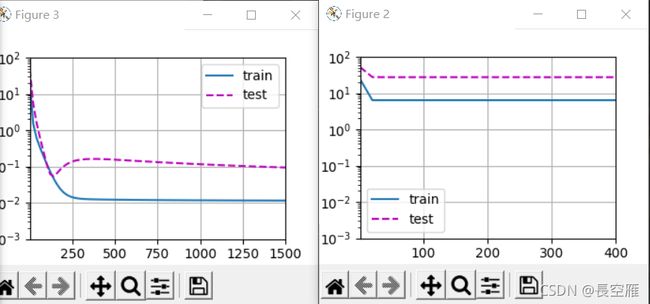
train(lambd=0)
plt.figure(1)
plt.plot
train(lambd=3)
plt.figure(2)
plt.plot
plt.show()
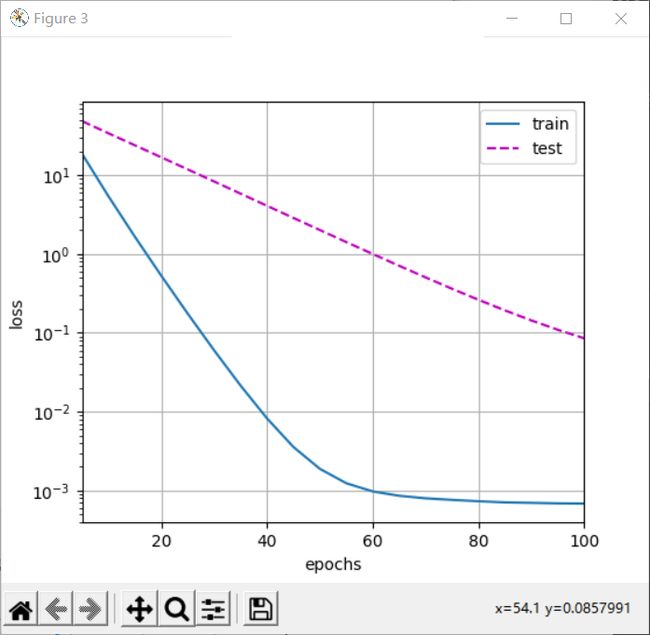
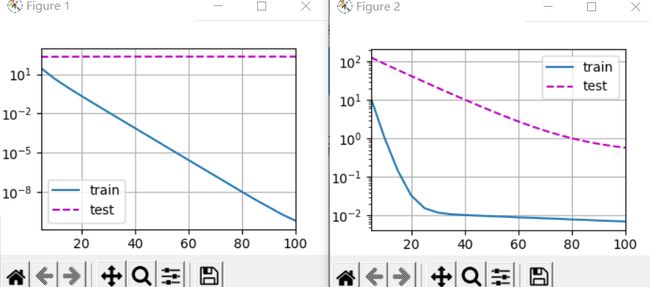
注意,在这里训练误差增大,但测试误差减小。这正是我们期望从正则化中得到的效果。过拟合得到改善。
6.3 简洁实现
def train_concise(wd):
net = nn.Sequential(nn.Linear(num_inputs, 1))
for param in net.parameters():
param.data.normal_()
loss = nn.MSELoss()
num_epochs, lr = 100, 0.003
# 偏置参数没有衰减。
trainer = torch.optim.SGD([
{"params": net[0].weight, 'weight_decay': wd},
{"params": net[0].bias}], lr=lr)
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
with torch.enable_grad():
trainer.zero_grad()
l = loss(net(X), y)
l.backward()
trainer.step()
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数:', net[0].weight.norm().item())
train_concise(wd=0)
plt.figure(1)
plt.plot
train_concise(wd=3)
plt.figure(2)
plt.plot
plt.show()
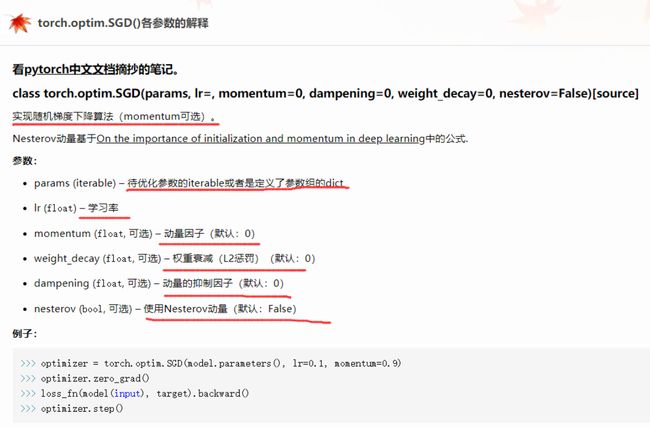
函数记录:
torch.optim.SGD([{"params": net[0].weight, 'weight_decay': wd},
{"params": net[0].bias}], lr=lr)
这些图看起来和我们从零开始实现权重衰减时的图相同。然而,它们运行得更快,更容易实现,对于更复杂的问题,这一好处将变得更加明显。