VGG论文阅读笔记

前言

    这次带来的是2014年ImageNet挑战赛分类问题的亚军，同时也是定位问题的冠军论文，VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION，就是大名鼎鼎的VGG啦。我将全文梳理一遍VGG的中心思想，并穿插一些自己的理解。下面给出一些阅读过程中对我有很大帮助的参考资料，以表示感谢，并附上VGG原文下载链接。
　　VGG 论文笔记
　　VGG论文原文重点提炼解析
　　卷积神经网络常见架构AlexNet、ZFNet、VGGNet、GoogleNet和ResNet模型
　　计算感受野的好用网址
　　深度学习VGG模型核心拆解
　　VGG-论文解读
　　VGG论文下载传送门

VGG论文阅读笔记

1 Introduction

    简要介绍了目前的卷积神经网络能够快速发展的原因（大规模数据集、硬件的发展如GPU）。提到了ImageNet挑战赛对卷积神经网络发展的推动作用。
　　由于AlexNet的成功，很多人开始对其进行改进。提到了ILSVRC-2013表现最好的方法，它在第一个卷积层使用了更小感受野的窗口和更小的步长。另有一篇论文提到在整个图像和多个尺度上改进网络的训练和测试过程。本文主要是研究网络深度对性能的影响。我们固定网络的其他超参数，通过增加卷积层的个数来缓慢增加网络的深度。该操作是可行的，原因是所有层都使用了一个较小的3*3卷积核（应该是网络做的比较深，如果使用太大的卷积核计算量太大，硬件不能支持，另外小卷积核确实会更有优势，后面会提到）。
　　我们的网络结构具有更高的准确率，不仅仅在ILSVRC比赛的分类问题和定位问题方面取得了state-of-the-art的效果，而且也适用于其他图像识别数据集，效果也不错。我们公布了两个性能最好的模型（应该就是VGG-16和VGG-19）。

2 ConvNet Configurations

    文章比较了几个不同深度的网络模型的性能，然后分析实验结果，最终得出结论。

2.1 Architecture

    训练时，网络的输入图像是224＊224的RGB图像，唯一的预处理操作是，在每个像素上减去训练集所有图像的RGB均值。所有卷积层使用3＊3的卷积核。在其中一个网络模型中，我们使用了1＊1的卷积核，这个可以看成是不同通道的一个线性组合（1＊1卷积后也要加非线性激活）。卷积的步长设置为1，padding使得卷积后图像大小不变（对于3＊3的卷积核来说padding设置为1）。网络共有5个最大池化层，最大池化层设置在一些卷积层的后面（并不是所有的卷积层后面都要做最大池化）。池化窗口为2＊2，步长为2。
　　卷积结束后连接三个全连接层，前两层有4096个通道，第三层有1000个通道（需要分1000类），最后输入一个softmax层。
　　所有激活函数使用relu。表格中有一个网络使用了LRN，但是本文发现LRN并不会提升网络的性能，反而会导致内存消耗增加以及计算时间的延长。

2.2 Configurations

    核心就是下面这张图。作者一共设计了6个不同结构的网络，分别给这些网络取了别名：A、A-LRN、B、C、D、E。可以看出，A包含了8个卷积层和3个全连接层，因此是11层带权重的网络（pooling里面没有权重）。后面网络的深度不断加深，最深的网络达到了19层。对于表中的符号，conv3-64表示这一层网络使用的是64个3＊3的卷积核，FC-4096代表是全连接层，有4096个神经元。
　　所有网络使用的都是3＊3的卷积核，有个别网络使用了1＊1的卷积核。网络的通道数都是从64开始，以2的倍数增加到512后就保持不变了。
　　另外Table 2中计算出了所有网络的参数总和，随着网络的加深，参数自然也是越来越多。

2.3 Discussion

    这部分论文提到，两层3＊3的卷积层感受野为5＊5区域（没有pooling），三层3＊3的卷积层感受野为7＊7区域（没有pooling）。一层7＊7的卷积层感受野也是7＊7。那么三层3＊3卷积层比一层7＊7卷积层有什么优势呢？按照原文的说法，优势有两个：
　　１、使用三个3＊3的卷积层代替一个7＊7的卷积层，会使得决策函数更具有判别性。这个更具有判别性怎么理解呢？根据我查到的资料，应该是把一个卷积层替换为三个卷积层，引入了更多的relu激活，从而增强了模型的非线性能力（一个卷积层只能有一个relu，但是三个卷积层可以有三个），这样使得CNN对特征的学习能力更强。
　　2、减少了网络参数。假设所有卷积层的通道数是C，那么三个3＊3的卷积层的参数总数是：
　　
而一个7＊7的卷积层的参数总数是：

后者比前者多了81%的参数，但是两者的感受野又都是相同的，前者还具有更多的relu。论文还提到，这种参数的减小还具有轻微的正则化效应。
　　此外，对于1＊1的卷积层，论文提到它可以在不影响模型感受野的情况下增加模型的非线性能力。文中提到了1＊1最近被用到了NIN网络上。
　　提到了最近的一些论文的研究成果。这些研究成果表明，使用小的卷积核和更深的网络结构往往能有更好的效果。特别提到了GoogLeNet，也是使用了更深的网络（22层）和小的卷积核（1＊1、3＊3和5＊5）。他们的网络拓扑结构比本文更复杂，在第一层feature map的空间分辨率减小得更厉害，这样能减小运算量。作者指出，在单个网络的分类精确度上，VGG要比GoogLeNet更好。

3 Classification Framework

3.1 Training

    优化目标是multinomial logistic regression objective，优化算法是mini-batch gradient descent with momentum。训练过程也采用了AlexNet中提到的权重衰减(weight decay)，衰减系数设置也一样（0.0005）。Dropout在前两个全连接层中使用（全连接越靠前往往参数越多，越需要使用Dropout），Dropout概率是0.5。初始学习率设置为0.01，每当验证集的分类准确率不再提高时，学习率都衰减一次，到之前的1/10（实验中学习率一共衰减了3次）。VGG相比AlexNet具有更深的网络结构和更多的参数，但是网络在更少的epoch后就收敛了，作者推测（注意是推测）原因是：
　　1、 更深的网络结构和更小的卷积核带来的轻微正则化的效果（3个3＊3的卷积层和一个7＊7的卷积层感受野一样但是参数更少，因此具有正则化效果。使用3个3＊3的卷积层代替一个7＊7的卷积层，既增加了网络深度（１层变为３层），又采用了更小的卷积核（7＊7变为3＊3），总的参数还减少了，因此作者说网络深度和小卷积核具有正则化效果）
　　2、 某些层的预初始化的结果（下文会提及）
　　对网络权重的初始化是很重要的，由于更深的网络，梯度具有不稳定性，不好的初始化算法会阻碍学习（例如使用sigmoid函数时会有梯度消失和梯度爆炸问题，导致学习缓慢；或者初始化一个很大的值，导致网络需要很多步迭代才能收敛）。本文由于网络深度较深，初始化就显得更加重要。本文采用的初始化方法是：首先随机初始化configuration A (表中11层的那个网络结构)，然后训练A，由于A尚且足够浅，因此不对其进行特殊的初始化操作。然后，训练更深的网络结构时（B、C、D、E），我们把网络的前4个卷积层和最后3个全连接层用A训练好的权重初始化（中间的层依然用随机初始化方法）。对于预初始化的层，我们不减小学习率，也允许他们在训练时更新。对于随机初始化的细节，我们的权重满足0均值0.01方差的正态分布。值得注意的是，在提交论文后我们才发现可以用Xavier (论文：Understanding the difficulty of training deep feedforward neural networks)进行初始化，这样就不需要使用预训练的权重初始化了。
　　 网络的输入图像尺寸固定为224＊224，输入图像通过随机裁剪rescale后的训练图像得到（每次迭代每张图像都做一次随机裁剪）。此外，为了进一步对数据集进行增广，本文采用了和AlexNet一样的数据增广方法（随机水平翻转和随机颜色通道变化）。关于训练集图像是如何rescale的，下面进行介绍（下面这部分VGG提出了单尺度的图像rescale训练方法和多尺度的图像rescale训练方法）。
　　 Training image size. 　设S是训练集图像rescale后图像的短边长度（S为训练尺度），由于输入图像是224＊224，原则上S不能小于224。S=224时裁剪的图像刚好能覆盖图像的短边，S>224时裁剪的图像对应原图的一个局部。
　　我们考虑两种rescale方法，第一种方法是固定S的大小，对应的是单尺度的训练。我们设置S=256 (AlexNet中也是这个大小)和S=384。对于一个网络结构，我们首先设置S=256进行训练，得到一个模型；之后设置S=384，用S=256的参数初始化这个模型，再设置一个较小的学习率（0.001），训练这个网络得到另一个模型。
　　第二种方法是通过对S的设置来完成一个多尺度的训练。每张训练图像都被随机rescale成S，S在[S_min,S_max]范围内随机取值（本文设置S_min= 256，S_max=512）。由于不同图像中被识别的物体是不同大小的，因此用多尺度的训练是更有好处的。这个多尺度的训练方法也可以认为是一种数据增广方法。通过这个多尺度的训练，我们训练出的单个网络模型可以识别一个不同大小的同个物体（翻译能力捉急，意思就是由于多尺度训练，输入图像可能是同一个目标但是经过了不同大小的缩放，因此训练出来的网络可以识别被缩放到不同程度的目标）。多尺度训练的网络，在初始化时用的是前面S=384的网络权重。

3.2 Testing

    在测试阶段，VGG的主要贡献是，将全连接层替换为卷积层，从而整个网络结构变为全卷积网络。好处是输入图像尺寸不再受限，测试阶段可以用比训练阶段尺寸更大的图像。
　　在测试阶段，首先预定义一个图像的短边长度为Q（测试尺度，与前面的S相呼应），测试图像会被rescale到Q。这里Q不一定非要等于S，我们会在Scet.4部分提到，对于每个S，设置多个Q的值可以提高网络的性能。
　　具体做法在我的LeNet论文阅读笔记中也提到过，全连接层可以看成是卷积核维度与上一层feature map维度完全一样的卷积层，卷积核的数量就是全连接层的神经元的数量。这样就可以把全连接层变为卷积层（这里我给全连接层替换为卷积层起个别名叫替换层）。测试阶段，当输入图像大小与训练阶段输入图像大小完全一致时，全卷积网络与带全连接的网络其实是完全等价的。当测试图像尺寸大于训练图像时，全卷积网络在替换层的输出与全连接层的输出维度就不一样了（这很容易理解，因为输入图像变大了嘛）。VGG的做法是将这个map求平均再输入进softmax。这个替换思想参考了OverFeat的工作，这里贴一张OverFeat的图辅助说明。

    由于全卷积网络不限制输入图像的大小，因此似乎就没有必要像AlexNet那样在测试时裁剪出图像的多个区域测试然后求预测的平均了（这里简称为多次裁剪预测法，全卷积网络的测试方法这里简称为密集预测法，对应的外文也正好是dense evaluation），而且这种多次裁剪预测法也比较耗时。不过论文提到，GoogLeNet的结果显示，多次裁剪预测法确实能提高预测准确率，因为多次裁剪相当于对输入图像做了更全面的采样，而全卷积网络只对一张图像进行了测试。那么作者认为多次裁剪预测法是对密集预测法的一个补充。
　　多次裁剪预测法和密集预测法的另一个区别在于进行卷积运算时的边界情况不同。多次裁剪预测法进行卷积时边界要填0，而密集预测法卷积时，对于在多次裁剪预测法中需要填0的地方，密集预测法由于输入图像变大，它实际上是知道这些地方的值是多少的，这样的话密集预测法会大大增加网络的感受野，捕获更多的背景信息。本文同时用两种方法进行测试，并比较两者的结果。

3.3 Implementation Details

    提到了多GPU训练的一些细节，将每个batch的图像分到多个GPU中，所有的GPU计算好各自的梯度后，求出整个batch的梯度均值，再更新权重。各个GPU的梯度计算是同步的，因此结果和在单个GPU中训练的结果是一样的。（当一张卡无法塞进一个batch的数据时，可以使用多GPU训练。例如batch size是8，用两张卡训练，每张卡塞进4个样本，两张卡分别求出梯度后再求梯度平均值作为整个batch的梯度）

4 Classification Experiments

    Dataset. 提到了数据集的划分，top-1和top-5误差等。

4.1 Single Scale Evaluation

    这部分设置Q只能取一个值（称为单尺度评估）。对于固定取值的S，设置Q=S；对于可变的S，即

取

实验结果如下表所示：

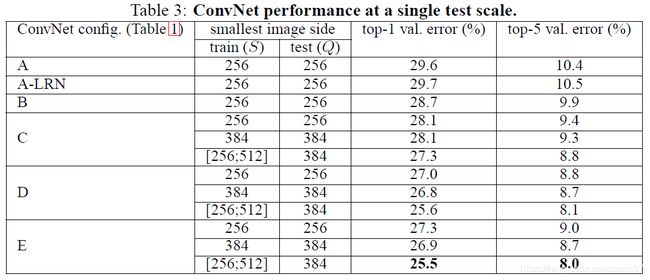
　　1、对比A和A-LRN的结果，可以看出，LRN并不能有效地提升网络的性能，因此文中提到，在后面的网络模型中也并没有采用LRN。
　　2、可以看到，随着网络深度的增加，误差在不断减小，
　　3、尽管C和D的网络深度一样，但是C性能比D差。C和D网络结构的区别是，C使用了1＊1的卷积核，但是D整个网络都是3＊3的卷积核。这表明1＊1卷积带来的额外的非线性效果确实起了作用（因为C比B好），但是使用具有一定大小感受野的卷积核来捕获空间信息也同样很重要（因为D比C好）。
　　4、文章还比较了两个感受野相同但深度不同的网络的运行结果（并未在表中给出，但是正文部分有叙述，附录Ｃ里面说这段其实是后加的）。一个5层的5＊5的网络，和一个10层的3＊3的网络（就是表中的B）。两个网络感受野大小都是21＊21（关于感受野的计算方法可以用我开篇提到的那个网址，很好用），但是浅网络的top-1 error比深网络（B）的top-1 error高出7%。由此可以看出，使用小卷积核的深网络要比大卷积核的浅网络效果更好。
　　5、对于单尺度评估，训练时采用尺度抖动（就是S在区间[256,512]内取值）比固定取值的S（S=256或S=384）效果更好。这表明通过尺度抖动进行数据增广确实对捕获不同尺度的图像信息有效。

4.2 Multi-scale Evaluation

    多尺度的评估通过把测试图像rescale到不同的尺度来实现（对应Q可以取多个值），同时需要最后将feature map求平均后输入softmax。考虑到如果训练集和测试集rescale的尺度差距很大的话，网络的性能会下降，因此对于S取固定值的情况（S=256或S=384），Q的取值范围是如下3个值：

　　对于训练时尺度抖动的情况，Q取如下3个值：
　　
　　实验结果如下：
　　
　　实验结果表明，在测试时也使用尺度抖动（即Q可以取不同的值），可以取得更好的效果（和单尺度评估相比）。最好的两个模型D和E表现完全相同，D有16层，应该就是VGG-16，E有19层，应该就是VGG-19。

4.3 Multi-crop Evaluation

    论文还比较了密集预测法和多次裁剪预测法，此外，又将两种预测方法的softmax输出求平均再预测。三种预测方法的实验结果如下表所示：

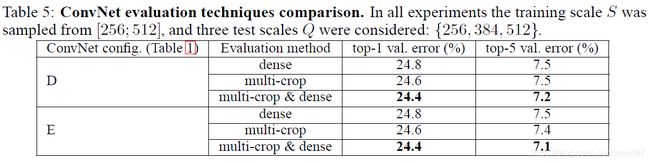
　　多次裁剪预测法性能比密集预测法更好一些，但是综合两者softmax输出预测的方法青出于蓝而胜于蓝，达到了最好的效果。作者猜想（又是猜想）原因是对待卷积边界处理方式的不同。

4.4 ConNet Fusion

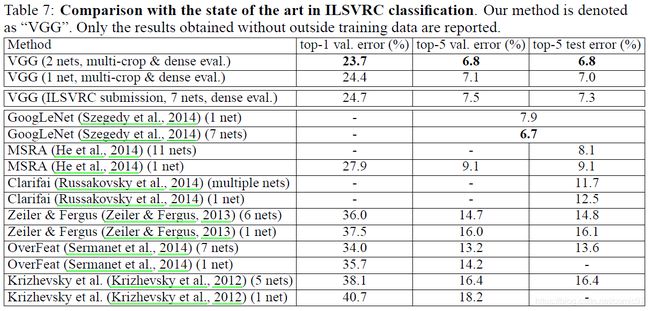
    这部分作者把不同模型的softmax输出求平均，应该是力图得到更低的top-1和top-5 error，希望能刷出更好的成绩。作者在提交成绩后又做了些改进，错误率最低已经能降到23.7%、6.8%和6.8%了。

4.5 Comparison with The State of The Art

    单个网络模型的性能来看，VGG是胜过GoogLeNet的，下表也能看出来：

5 Conclusion

    可能是论文经过了多次修改的缘故，总觉得原文的总结不太全面，这里我自己写下总结好了。本文主要讨论了一下几个概念：
　　1、网络深度和卷积核大小对网络性能的影响
　　2、训练时的单、多尺度方法（S固定或S取一个范围内的值）
　　3、测试时的多次裁剪预测法和密集预测法（密集预测法要使用全卷积网络）
　　4、测试时的单、多尺度评估（Q固定或Q可以取多个值）

附录

    后续的附录介绍了VGG对于定位问题的解决方法，以及在其他数据集上的性能评估，应该是想要证明VGG具有很好的泛化能力，可以适用于很多不同的深度学习问题。