GeoDa 空间自相关操作步骤
GeoDa空间自相关操作步骤
- 前言
-
- GeoDa软件与下载
- 目标
- 理解空间自相关
- Geoda空间自相关计算步骤
练习数据获取
关注cshgiser公众号,回复“路网密度”获取~
前言
GeoDa软件与下载
GeoDaGeoDa是一个免费的开源软件工具,是进行空间数据分析的强有力软件,最具特色的应该是空间自相关的计算,除此之外,软件本身集成了很多空间数据探索分析方法。
目标
逐步利用Geoda计算莫兰指数
理解空间自相关
依据“越相近,越相似”的原理(地理学第一定律),空间现象普遍存在自相关性。
以GDP为例,一个地区的GDP高,它周围的区域很难完全独立于该区域,可能存在下面两种情况:
(1)它周围区域的GDP都很高(正相关),可能是共享了某个有利的客观条件,如沿海区域GDP都倾向于较高。
(2)它周围的区域GDP都很低(负相关),假设该区域具有很强的城市吸引力,将资源从周边区域吸收出去,则会造成这种局势。
无论哪种情况,区域上的相近会造成某种属性相似,这就是空间自相关。为了度量空间自相关,Moran在1984年提出一个指数来反映空间邻接或空间邻近的区域单元属性值的相似程度。
莫兰指数I的定义式如下:

可以不用懂上面这个式子,只需要知道它需要输入什么数据,得到什么结果。
结果比较简单:和相关系数一样,值域为-1~1,越接近于-1,负相关性越大;越接近于1,正相关性越大。
然后看一下它需要什么输入:也比较简单,由于是“自相关”,只需要输入一个变量。另外就是如何体现“空间”,其核心是空间权重矩阵的确定。
空间权重矩阵以0或1的方式标记两者是否邻接,来体现空间关系,确定邻接方式有两种。
第一种为多边形邻接(如处理的数据为面状要素):定义两个要素有公共线为相邻,定义权重为1,或者两个要素二阶相邻(相邻的相邻)。
第二种为距离邻接(如处理的数据为点状要素):即在一定距离范围内相邻,这个距离可以是简单的欧氏距离也可以是复杂的线段距离(基于路网等等)。
一个熟练的应用者应在定义权重矩阵上下功夫,懂的权重矩阵的含义,从实际问题出发,基于一定假设,构建合适的权重矩阵。后续的结果分析中,同样需要了解所定义的权重。至于其他,则可以无脑输入。
虽然莫兰指数能够判断出空间上的整体分布情况,但事实难以探测出聚集的位置所在及区域相关程度。为了反映整个大区域中的局部指标,需要进一步分析局部空间自相关。通常包括:空间联系的局部指标(Local Indicators of Spatial Association,LISA)、Moran散点图。
同样不需要懂上面这个式子,只要理解通过上面这个式子可以计算得到每个要素对应的局部莫兰指数值,同时经过显著性检验可以知道哪些是结果是显著的。由此生成一个空间分布图(LISA图)呈现出不同的聚集特征。
莫兰散点图是Anselin在1996年首次提出的,所拟合的回归直线的斜率即为莫兰指数。

如图为一个莫兰散点图,散点图的横轴为变量的值与均值的偏差,纵轴为邻居要素的变量的值与均值的偏差。可能理解起来比较抽象,可以直接看结论:
与局部莫兰指数相比,莫兰散点图的重要优势在于能够进一步具体区分每个要素与其邻居要素之间的关系,包括高值-高值(落在第一象限)、低值-低值(落在第三象限)、**高值-低值(落在第四象限)和低值-高值(落在第二象限)**四种空间联系形式。这样能够更清晰的知道,一个区域周围分布的是高值区域和低值区域,这在实际问题的分析中具有重要参考价值。
Geoda空间自相关计算步骤

2. 构建权重矩阵。点击Create Weights按钮就可以进入权重构建页面,如下图所示:

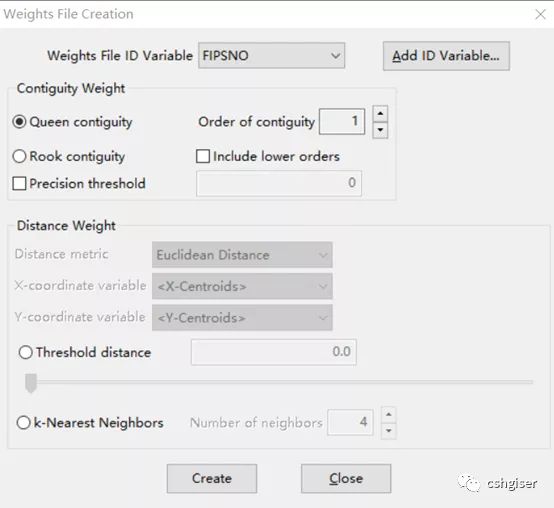
这里有几个选项,可以根据需求选择:
(1)Weights File ID Variable:变量标识,是属性表中的某一列,用于标识对象,所以需要值唯一。当然也可以点击Add ID Variable 创建新的标识列。
(2)确定权重邻接形式。第一种为多边形邻接确定权重(a);第二种为距离邻接确定权重(b)。这两种方法选择其中一个。
(a)多边形邻接确定权重参数设置
Rook contiguity和Queen contiguity,这两个参数点选其一。

rook和queen国际象棋术语。rook, 横、竖均可以走,步数不受限制,不能斜走(和中国象棋类似),不能越子。queen, 横、直、斜都可以走,步数不受限制,但是,不能越子行棋。该棋也是棋力最强的棋子。差别看上图就清楚了。
Order of contiguity,该参数定义几阶邻接,默认就是一阶。两阶邻接就是一个多边形邻接的邻接也在距离之内,依此类推。
(b)距离邻接确定权重参数设置。
Threshold distance为距离阈值,超出阈值判别为不邻接。
Distance metric距离度量方式,包括欧几里得距离(Euclidean distance,直线距离),输入两个坐标就能算出;弧段距离(Arc distance),主要针对没有投影,如用经纬度的图层,这类图层不能用经纬度坐标直接计算欧氏距离,因此引入考虑地球曲率的弧段距离。不过,还是建议在做与距离有关的分析时,首先对图层进行投影。
X-coordinate variable和Y-coordinate variable为坐标变量,就是每个要素的实际位置,如果是多边形一般取的就是质心坐标了。
这里以多边形rook邻接方式构建权重矩阵,构建好的权重矩阵文件,用写字板打开如下:

虽然是权重矩阵文件,但是并没有以矩阵的形式存储,因为存储大量的0和1会占据大量内存空间。这个文件以两行为一个单元存储了每个元素的邻居元素,例如可以看出27077这个对象有3个邻接,分别为27007,20135和27071。
3. 计算全剧莫兰指数。点击Univariate Moran’s I 进入莫兰指数计算界面,首先是确定变量。

我们这里以UE90这个变量为例,含义为1990的失业率。

计算得到莫兰指数为0.543.

理解散点图:这里引入一个变量z,含义为变量UE90偏离均值的大小,所以整体上分布在0值两边。同是z也就是横轴变量,而纵轴变量为邻接要素的变量值乘以对应归一化权重值的和,反映的是邻居要素的整体水平。由此可见,落在第一象限,无论是该元素还是它的邻居元素,UE90均比较大(相对均值来说),体现一种高-高分布的格局;而第二象限内,该元素UE90比较小,它的邻居元素变量值又比较大,呈现一种低-高的空间分布格局。
这个散点图为莫兰散点图,是Anselin在1996年首次提出的,所拟合的回归直线的斜率即为莫兰指数。
4. 显著性评估


通过随机生成空间数据,来看是否能够拒绝空间随机性的零假设,由上图可以看出,黄色的线(I=0.543)较远地落在特定P值下随机分布的右侧,表明该统计结果比较显著。
5. 计算局部莫兰指数。点击univariate Local Moran’s I 进入局部莫兰指数计算界面,首先是确定变量。
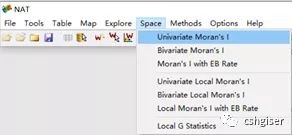
在执行局部莫兰指数计算时,可以勾选三个显示结果,分别为显著性图、聚集分布图和莫兰散点图,实际上莫兰散点图在计算全局空间自相关时已经显示,这里勾选前两个选项。

这两个图,上面为聚集图,有四种空间联系方式,包括高值-高值(莫兰散点图中落在第一象限的区域)、低值-低值(第三象限)、高值-低值(第四象限)和低值-高值(第二象限)。同时该聚集图只显示了显著的区域。
下面为对应的显著性水平,表明每个区域对应的局部相关值是否显著。


