ID3算法决策树(java实现)
文章目录
- 前言
- 预备知识
-
- 一.什么是分类问题?
- 二.训练集与测试集
- 三.什么是决策树
- 四.原理
- 正文
-
- 一.ID3算法
-
- 所使用的样本数据有一定的要求:
- 属性选择:
-
- ID3决定哪些属性如何是最好的?
- 二.信息熵
- 三.构建决策树
-
- 1.用属性构建节点:
- 2.选取度量指标:熵/基尼系数
- 3.节点排序
- 四.决策树的剪枝策略
-
- 剪枝的目的:
- 剪枝策略:
-
- 预剪枝:
-
- 实现方法:
- 后剪枝:
-
- 实现方法:
- 代码实现
-
- 实验数据:
- 实验用的数据文件(arff文件):
- 程序代码:
- 最终生成的文件如下(xml文件):
- 树状图:
前言
决策树模型是机器学习的各种算法模型中比较好理解的一种模型。
它的基本原理是通过对一系列问题进行if/else的推导,最终实现相关决策。
决策树的概念并不复杂,主要是通过连续的逻辑判断得出最后的结论,其关键在于如何建立这样一棵“树”
预备知识
一.什么是分类问题?
通过一条数据的属性来预测该数据的类型的问题
二.训练集与测试集
数据挖掘时,会将数据的70%用于训练,将30%的数据用于测试
三.什么是决策树
决策树是用于解决分类问题的一种算法
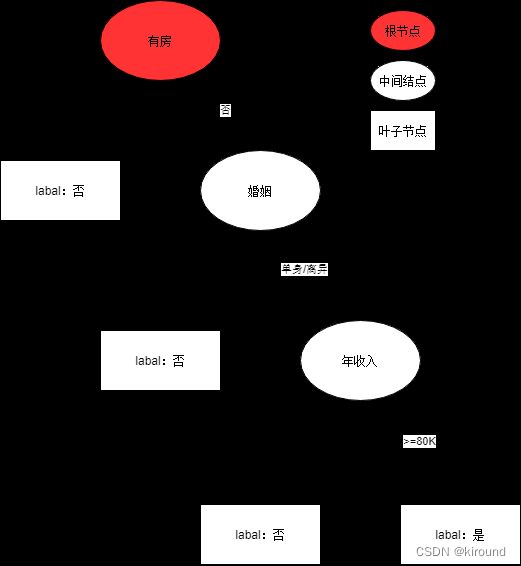
四.原理
数据:
| ID | 有房 | 婚姻 | 年收入 | 拖欠贷款 |
|---|---|---|---|---|
| 1 | 是 | 单身 | 125K | 否 |
| 2 | 否 | 已婚 | 100K | 否 |
| 3 | 否 | 单身 | 70K | 否 |
| 4 | 是 | 已婚 | 120K | 否 |
| 5 | 否 | 离异 | 95K | 是 |
| 6 | 否 | 已婚 | 60K | 否 |
| 7 | 是 | 离异 | 220K | 否 |
| 8 | 否 | 单身 | 85K | 否 |
| 9 | 否 | 已婚 | 75K | 否 |
| 10 | 否 | 单身 | 90K | 否 |
- 根节点:无入多出
- 中间节点:一入多出
- 叶子节点:一入无出
正文
一.ID3算法
ID3算法是一种贪心算法,用来构造决策树。
ID3算法起源于概念学习系统(CLS),以信息熵的下降速度为选取测试属性的标准,即在每个节点选取还尚未被用来划分的具有最高信息增益的属性作为划分标准,然后继续这个过程,直到生成的决策树能完美分类训练样例。
所使用的样本数据有一定的要求:
- 描述-属性-值
相同的属性必须描述每个例子和有固定数量的价值观。 - 预定义类
实例的属性必须已经定义的,也就是说,他们不是学习的ID3。 - 离散类
类必须是尖锐的鲜明。连续类分解成模糊范畴(如金属被“努力,很困难的,灵活的,温柔的,很软”都是不可信的。 - 足够的例子
因为归纳概括用于(即不可查明)必须选择足够多的测试用例来区分有效模式并消除特殊巧合因素的影响。
属性选择:
ID3决定哪些属性如何是最好的?
一个统计特性,被称为信息增益,为了明确增益,我们首先从信息论借用一个定义,叫做熵。每个属性都有一个熵。使用熵得到给定属性衡量培训例子带入目标类分开。信息增益最高的信息(该信息是最有益的分类)被选择。
二.信息熵
根据《统计学习方法》中的描述,G(D,A)表示数据集D在特征A的划分下的信息增益。
具体公式: G(D,A)=H(D)-H(D|A)。
- 其中H(D)表示数据集D(测试集)的熵,熵可以用来描述其混乱度,计算公式为:
H ( D ) = ∑ k = 1 k − ( ∣ D k ∣ ∣ D ∣ ∗ log 2 ∣ D k ∣ ∣ D ∣ ) H\left (D \right ) = \sum_{k=1}^{k} - \left ( \frac{\left | D_{k} \right | }{\left | D\right | }\ast \log_{2}{\frac{\left | D_{k} \right | }{\left | D \right | } } \right ) H(D)=k=1∑k−(∣D∣∣Dk∣∗log2∣D∣∣Dk∣)
(log函数一般以2为底)
可见对于数据集D而言,|Dk|表示类别为k的数量,其类别越多,越混乱。
- H(D|A)表示数据集D在A的划分下的的不确定性,计算公式为:
H ( D ∣ A ) = − ∑ i = 1 n ∣ D i ∣ ∣ D i ∣ ∗ ∑ k = 1 k ( ∣ D i k ∣ ∣ D i ∣ ∗ log 2 ∣ D i k ∣ ∣ D i ∣ ) H \left (D | A \right ) = - \sum_{i=1}^{n} \frac{\left | D_{i} \right | }{\left | D_{i} \right | } * \sum_{k=1}^{k} \left ( \frac{\left | D_{ik} \right | }{\left | D_{i} \right | }\ast \log_{2}{\frac{\left | D_{ik} \right | }{\left | D_{i} \right | } } \right ) H(D∣A)=−i=1∑n∣Di∣∣Di∣∗k=1∑k(∣Di∣∣Dik∣∗log2∣Di∣∣Dik∣)
|Dik|表示在特征A中value为i的划分下数据集类别为k的数量。
他们的差也即是信息增益,表示由于特征A使得数据集D的分类的不确定减少的差,所以这个值越大说明A的分类对D越有效,也就是权重越大。
三.构建决策树
1.用属性构建节点:
- 二元属性:二元划分
- 多元属性:组合某几类组成二元划分或直接进行多元划分
- 顺序属性:可以选取合适的分隔值进行二元划分或多元划分
当遇到连续值时,可以对其进行离散化:数列进行排序后,对每个划分计算熵值增益,选取其中熵值增益最大的。
2.选取度量指标:熵/基尼系数
3.节点排序
- 1)计算最初测试集的熵值(H(D))
- 2)计算每个属性的信息增益,选出信息增益最大的(熵值最小)的划分属性
- 3)计算每个属性的信息增益,依次选取每次划分后熵值增益最大的属性作为中间节点
四.决策树的剪枝策略
剪枝的目的:
决策树的过拟合风险较大,为减小过拟合风险,必须进行剪枝
过拟合:训练表现极好,但测试误差过大
由于决策树可以无限细分,到极致时每个叶子节点只有一个元素,达成过拟合
虽然熵值为0,但没有意义
剪枝策略:
预剪枝:
边建立决策树边剪枝(更实用)
实现方法:
限制深度(树的高度)、叶子节点的个数,叶子节点样本数,信息增益量(划分程度)等通过实验进行选值
后剪枝:
建立决策树完成后进行剪枝操作
实现方法:
衡量标准:
C α ( T ) = C ( T ) + α ⋅ ∣ T l e a f ∣ C_{ \alpha } \left ( T \right ) = C \left ( T \right ) + \alpha \cdot \left | T_{leaf} \right | Cα(T)=C(T)+α⋅∣Tleaf∣
叶子节点越多,损失越大
α:自定义值、C:熵值
代码实现
实验数据:
| outlook | temperature | humidity | windy | play | |||||||||
| yes | no | yes | no | yes | no | yes | no | yes | no | ||||
| sunny | 2 | 3 | hot | 2 | 2 | high | 3 | 4 | FALSE | 6 | 2 | 9 | 5 |
| overcast | 4 | 0 | mild | 4 | 2 | normal | 6 | 1 | TRUR | 3 | 3 | ||
| rainy | 3 | 2 | cool | 3 | 1 | ||||||||
实验用的数据文件(arff文件):
@relation weather.symbolic
@attribute outlook {sunny, overcast, rainy}
@attribute temperature {hot, mild, cool}
@attribute humidity {high, normal}
@attribute windy {TRUE, FALSE}
@attribute play {yes, no}
@data
sunny,hot,high,FALSE,no
sunny,hot,high,TRUE,no
overcast,hot,high,FALSE,yes
rainy,mild,high,FALSE,yes
rainy,cool,normal,FALSE,yes
rainy,cool,normal,TRUE,no
overcast,cool,normal,TRUE,yes
sunny,mild,high,FALSE,no
sunny,cool,normal,FALSE,yes
rainy,mild,normal,FALSE,yes
sunny,mild,normal,TRUE,yes
overcast,mild,high,TRUE,yes
overcast,hot,normal,FALSE,yes
rainy,mild,high,TRUE,no
程序代码:
package DemoJueCeShu;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.FileWriter;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
import java.util.regex.Matcher;
import java.util.regex.Pattern;
import org.dom4j.Document;
import org.dom4j.DocumentHelper;
import org.dom4j.Element;
import org.dom4j.Node;
import org.dom4j.io.OutputFormat;
import org.dom4j.io.XMLWriter;
public class ID3 {
private ArrayList<String> attribute = new ArrayList<String>(); // 存储属性的名称
private ArrayList<ArrayList<String>> attributevalue = new ArrayList<ArrayList<String>>(); // 存储每个属性的取值
private ArrayList<String[]> data = new ArrayList<String[]>();; // 原始数据
int decatt; // 决策变量在属性集中的索引
public static final String patternString = "@attribute(.*)[{](.*?)[}]";
Document xmldoc;
Element root;
public ID3() {
xmldoc = DocumentHelper.createDocument();
root = xmldoc.addElement("root");
root.addElement("DecisionTree").addAttribute("value", "null");
}
public static void main(String[] args) {
ID3 inst = new ID3();
inst.readARFF(new File("D:/data/Java Project/LearningProject/com.JavaWebBasics/src/DemoJueCeShu/weather.nominal.arff"));
inst.setDec("play");
LinkedList<Integer> ll=new LinkedList<Integer>();
for(int i=0;i<inst.attribute.size();i++){
if(i!=inst.decatt)
ll.add(i);
}
ArrayList<Integer> al=new ArrayList<Integer>();
for(int i=0;i<inst.data.size();i++){
al.add(i);
}
inst.buildDT("DecisionTree", "null", al, ll);
inst.writeXML("D:/data/Java Project/LearningProject/com.JavaWebBasics/src/DemoJueCeShu/dt.xml");
return;
}
//读取arff文件,给attribute、attributevalue、data赋值
public void readARFF(File file) {
try {
FileReader fr = new FileReader(file);
BufferedReader br = new BufferedReader(fr);
String line;
Pattern pattern = Pattern.compile(patternString);
while ((line = br.readLine()) != null) {
Matcher matcher = pattern.matcher(line);
if (matcher.find()) {
attribute.add(matcher.group(1).trim());
String[] values = matcher.group(2).split(",");
ArrayList<String> al = new ArrayList<String>(values.length);
for (String value : values) {
al.add(value.trim());
}
attributevalue.add(al);
} else if (line.startsWith("@data")) {
while ((line = br.readLine()) != null) {
if(line=="")
continue;
String[] row = line.split(",");
data.add(row);
}
} else {
continue;
}
}
br.close();
} catch (IOException e1) {
e1.printStackTrace();
}
}
//设置决策变量
public void setDec(int n) {
if (n < 0 || n >= attribute.size()) {
System.err.println("决策变量指定错误。");
System.exit(2);
}
decatt = n;
}
public void setDec(String name) {
int n = attribute.indexOf(name);
setDec(n);
}
//给一个样本(数组中是各种情况的计数),计算它的熵
public double getEntropy(int[] arr) {
double entropy = 0.0;
int sum = 0;
for (int i = 0; i < arr.length; i++) {
entropy -= arr[i] * Math.log(arr[i]+Double.MIN_VALUE)/Math.log(2);
sum += arr[i];
}
entropy += sum * Math.log(sum+Double.MIN_VALUE)/Math.log(2);
entropy /= sum;
return entropy;
}
//给一个样本数组及样本的算术和,计算它的熵
public double getEntropy(int[] arr, int sum) {
double entropy = 0.0;
for (int i = 0; i < arr.length; i++) {
entropy -= arr[i] * Math.log(arr[i]+Double.MIN_VALUE)/Math.log(2);
}
entropy += sum * Math.log(sum+Double.MIN_VALUE)/Math.log(2);
entropy /= sum;
return entropy;
}
public boolean infoPure(ArrayList<Integer> subset) {
String value = data.get(subset.get(0))[decatt];
for (int i = 1; i < subset.size(); i++) {
String next=data.get(subset.get(i))[decatt];
//equals表示对象内容相同,==表示两个对象指向的是同一片内存
if (!value.equals(next))
return false;
}
return true;
}
// 给定原始数据的子集(subset中存储行号),当以第index个属性为节点时计算它的信息熵
public double calNodeEntropy(ArrayList<Integer> subset, int index) {
int sum = subset.size();
double entropy = 0.0;
int[][] info = new int[attributevalue.get(index).size()][];
for (int i = 0; i < info.length; i++)
info[i] = new int[attributevalue.get(decatt).size()];
int[] count = new int[attributevalue.get(index).size()];
for (int i = 0; i < sum; i++) {
int n = subset.get(i);
String nodevalue = data.get(n)[index];
int nodeind = attributevalue.get(index).indexOf(nodevalue);
count[nodeind]++;
String decvalue = data.get(n)[decatt];
int decind = attributevalue.get(decatt).indexOf(decvalue);
info[nodeind][decind]++;
}
for (int i = 0; i < info.length; i++) {
entropy += getEntropy(info[i]) * count[i] / sum;
}
return entropy;
}
// 构建决策树
public void buildDT(String name, String value, ArrayList<Integer> subset,
LinkedList<Integer> selatt) {
Element ele = null;
@SuppressWarnings("unchecked")
List<Node> list = root.selectNodes("//"+name);
Iterator<Node> iter=list.iterator();
while(iter.hasNext()){
ele= (Element) iter.next();
if(ele.attributeValue("value").equals(value))
break;
}
if (infoPure(subset)) {
ele.setText(data.get(subset.get(0))[decatt]);
return;
}
int minIndex = -1;
double minEntropy = Double.MAX_VALUE;
for (int i = 0; i < selatt.size(); i++) {
if (i == decatt)
continue;
double entropy = calNodeEntropy(subset, selatt.get(i));
if (entropy < minEntropy) {
minIndex = selatt.get(i);
minEntropy = entropy;
}
}
String nodeName = attribute.get(minIndex);
selatt.remove(new Integer(minIndex));
ArrayList<String> attvalues = attributevalue.get(minIndex);
for (String val : attvalues) {
ele.addElement(nodeName).addAttribute("value", val);
ArrayList<Integer> al = new ArrayList<Integer>();
for (int i = 0; i < subset.size(); i++) {
if (data.get(subset.get(i))[minIndex].equals(val)) {
al.add(subset.get(i));
}
}
buildDT(nodeName, val, al, selatt);
}
}
// 把xml写入文件
public void writeXML(String filename) {
try {
File file = new File(filename);
if (!file.exists())
file.createNewFile();
FileWriter fw = new FileWriter(file);
OutputFormat format = OutputFormat.createPrettyPrint(); // 美化格式
XMLWriter output = new XMLWriter(fw, format);
output.write(xmldoc);
output.close();
} catch (IOException e) {
System.out.println(e.getMessage());
}
}
}
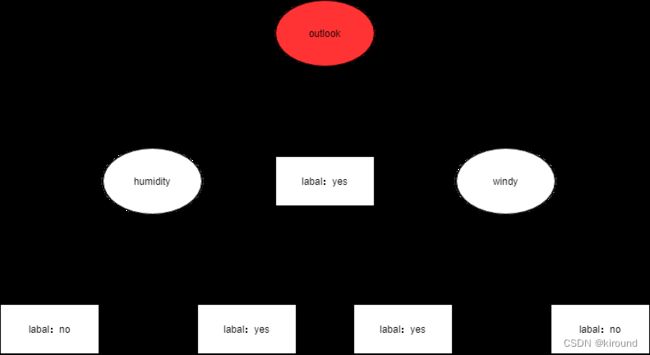
最终生成的文件如下(xml文件):
no
yes
yes
no
yes