机器学习笔记之支持向量机(SVM)
机器学习笔记之支持向量机(SVM)
-
- 基本概念
- SVM线性分类器
- SVM的优化目标
- KKT条件
- SMO求解对偶问题:
- 核函数
- 软间隔和正则化
- 代码实现
基本概念
线性可分SVM——线性 SVM——非线性 SVM
1、线性可分SVM,表示可以用一根线非常清晰的划分两个区域;线到支持向量的距离 d 就是最小的。
2、线性 SVM,表示用一根线划分区域后,可能存在误判点,但还是线性的;线到支持向量的距离不一定是最小的,但忽略其他非规则的支持向量。
3、非线性 SVM,表示使用核函数之后,把低维的非线性转换为高维线性(相当于将低维非线性以核函数为基底表示高维空间中线性)
SVM线性分类器
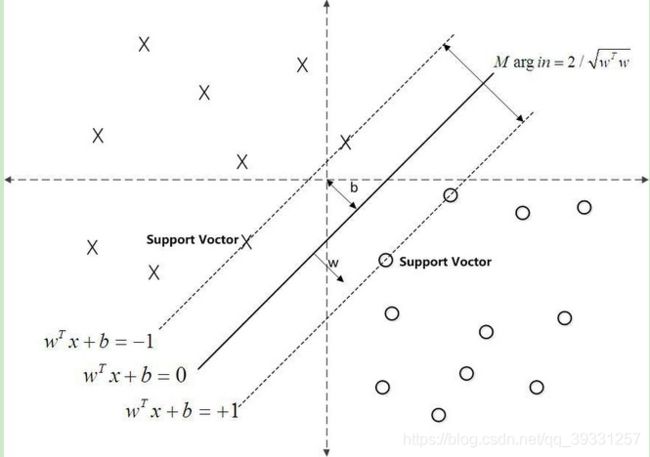
SVM从线性可分情况下的最优分类面发展而来。最优分类面就是要求分类线不但能将两类正确分开(训练错误率为0),且使分类间隔最大。SVM考虑寻找一个满足分类要求的超平面,并且使训练集中的点距离分类面尽可能的远,也就是寻找一个分类面使它两侧的空白区域最大。线性可分支持向量机就对应着能将数据正确划分并且间隔最大的直线。
能够容忍更多噪声—>所有样本与分割超平面的距离尽可能远—>最差的样本(离分割超平面最近的样本)与分割超平面的距离要尽可能远。SVM的目的就是从无数个分割超平面中,找到最好的分割超平面。

SVM的优化目标
在样本空间中,划分超平面可通过如下线性方程来描述:![]()
写成向量形式:f(x)= wT x+b
其中w为法向量决定了超平面的方向;b为位移项,决定了超平面原点之间的距离
下面我们将超平面记为(w,b)。
样本空间中任意点x到超平面(w,b)的距离为:
假设超平面(w,b)能将训练样本正确分类,即对于y=1,w’x+b>0;y=-1,w`x+b<0。
距离超平面最近的几个点使=1和=-1成立,这些点对应的向量称为支持向量。
支持向量到超平面的距离为 : ,两个支持向量之间的距离(称为间隔)为:
,两个支持向量之间的距离(称为间隔)为:
想要找到最大间隔的超平面,就是找w和b使得r最大,即:max ![]()
即优化问题为
在一定的约束条件下,目标最优,损失最小。
由于这个问题的特殊结构,可以通过拉格朗日对偶性变换到对偶变量的优化问题,通过求解与原问题等价的对偶问题得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法。
lagrange法求极值,将约束条件融合到目标函数中:
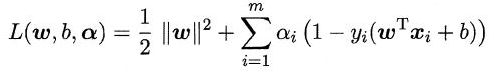
再将L分别对w,b求偏导等于0: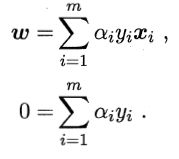
代入原始问题得到对偶问题消去w,b:
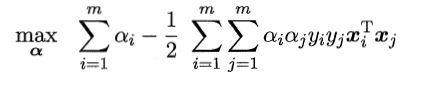
即: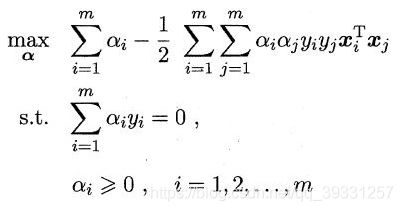
代入函数得:

KKT条件
SMO求解对偶问题:
固定α以外的所有参数,求α的极值。通过约束条件,可以用其它变量将α进行表示。
重复以下两步:
- 选取αi、αj
- 固定其它参数,解对偶问题并更新αi、αj
αi、αj有一个不满足KKT条件的时候,目标函数就在迭代后减小。违背程度大则变量更新后的目标函数减幅越大。
核函数
现实任务中,原始样本空间中也许不存在一个可以正确划分两类样本的超平面,但可以通过映射将原始空间映射到更高纬度的空间,进而使得样本在特征空间中线性可分。

但是要计算两个x在映射空间的内积比较困难,因为特征空间的往往是高维的。所以我们设想这样的一个函数:
![]()
即两个x在映射空间的内积等于其原始空间中通过k函数计算的结果。这个k函数就是核函数。
常用核函数:

软间隔和正则化
现实任务中很难找到核函数使得训练集完全线性可分,且完全的线性可分也可能是过拟合的结果。
为了应对这一问题,允许向量机在一些样本上出错。引入了软间隔的概念。
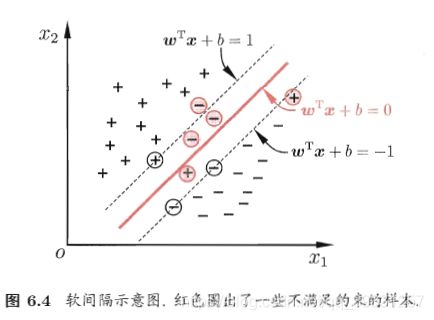
软间隔允许有部分分类错误的点![]()
但要使得分类错误的点尽可能少,即:

0/1损失函数的函数性质不佳,不宜求解。通常使用一些替代函数来替换损失函数,他们通常是0/1损失函数的上界。

代码实现
svm_train.py代码:
# coding:UTF-8
import numpy as np
import svm
def load_data_libsvm(data_file):
'''导入训练数据
input: data_file(string):训练数据所在文件
output: data(mat):训练样本的特征
label(mat):训练样本的标签
'''
data = []
label = []
f = open(data_file)
for line in f.readlines():
lines = line.strip().split(' ')
# 提取得出label
label.append(float(lines[0]))
# 提取出特征,并将其放入到矩阵中
index = 0
tmp = []
for i in range(1, len(lines)):
li = lines[i].strip().split(":")
if int(li[0]) - 1 == index:
tmp.append(float(li[1]))
else:
while(int(li[0]) - 1 > index):
tmp.append(0)
index += 1
tmp.append(float(li[1]))
index += 1
while len(tmp) < 13:
tmp.append(0)
data.append(tmp)
f.close()
return np.mat(data), np.mat(label).T
if __name__ == "__main__":
# 1、导入训练数据
print("------------ 1、load data --------------")
dataSet, labels = load_data_libsvm("heart_scale")
# 2、训练SVM模型
print("------------ 2、training ---------------")
C = 0.6
toler = 0.001
maxIter = 500
svm_model = svm.SVM_training(dataSet, labels, C, toler, maxIter)
# 3、计算训练的准确性
print("------------ 3、cal accuracy --------------")
accuracy = svm.cal_accuracy(svm_model, dataSet, labels)
print("The training accuracy is: %.3f%%" % (accuracy * 100))
# 4、保存最终的SVM模型
print("------------ 4、save model ----------------")
svm.save_svm_model(svm_model, "model_file")
svm.py代码:
#coding:UTF-8
import numpy as np
import pickle
class SVM:
def __init__(self, dataSet, labels, C, toler, kernel_option):
self.train_x = dataSet # 训练特征
self.train_y = labels # 训练标签
self.C = C # 惩罚参数
self.toler = toler # 迭代的终止条件之一
self.n_samples = np.shape(dataSet)[0] # 训练样本的个数
self.alphas = np.mat(np.zeros((self.n_samples, 1))) # 拉格朗日乘子
self.b = 0
self.error_tmp = np.mat(np.zeros((self.n_samples, 2))) # 保存E的缓存
self.kernel_opt = kernel_option # 选用的核函数及其参数
self.kernel_mat = calc_kernel(self.train_x, self.kernel_opt) # 核函数的输出
def cal_kernel_value(train_x, train_x_i, kernel_option):
'''样本之间的核函数的值
input: train_x(mat):训练样本
train_x_i(mat):第i个训练样本
kernel_option(tuple):核函数的类型以及参数
output: kernel_value(mat):样本之间的核函数的值
'''
kernel_type = kernel_option[0] # 核函数的类型,分为rbf和其他
m = np.shape(train_x)[0] # 样本的个数
kernel_value = np.mat(np.zeros((m, 1)))
if kernel_type == 'rbf': # rbf核函数
sigma = kernel_option[1]
if sigma == 0:
sigma = 1.0
for i in range(m):
diff = train_x[i, :] - train_x_i
kernel_value[i] = np.exp(diff * diff.T / (-2.0 * sigma**2))
else: # 不使用核函数
kernel_value = train_x * train_x_i.T
return kernel_value
def calc_kernel(train_x, kernel_option):
'''计算核函数矩阵
input: train_x(mat):训练样本的特征值
kernel_option(tuple):核函数的类型以及参数
output: kernel_matrix(mat):样本的核函数的值
'''
m = np.shape(train_x)[0] # 样本的个数
kernel_matrix = np.mat(np.zeros((m, m))) # 初始化样本之间的核函数值
for i in range(m):
kernel_matrix[:, i] = cal_kernel_value(train_x, train_x[i, :], kernel_option)
return kernel_matrix
def cal_error(svm, alpha_k):
'''误差值的计算
input: svm:SVM模型
alpha_k(int):选择出的变量
output: error_k(float):误差值
'''
output_k = float(np.multiply(svm.alphas, svm.train_y).T * svm.kernel_mat[:, alpha_k] + svm.b)
error_k = output_k - float(svm.train_y[alpha_k])
return error_k
def update_error_tmp(svm, alpha_k):
'''重新计算误差值
input: svm:SVM模型
alpha_k(int):选择出的变量
output: 对应误差值
'''
error = cal_error(svm, alpha_k)
svm.error_tmp[alpha_k] = [1, error]
def select_second_sample_j(svm, alpha_i, error_i):
'''选择第二个样本
input: svm:SVM模型
alpha_i(int):选择出的第一个变量
error_i(float):E_i
output: alpha_j(int):选择出的第二个变量
error_j(float):E_j
'''
# 标记为已被优化
svm.error_tmp[alpha_i] = [1, error_i]
candidateAlphaList = np.nonzero(svm.error_tmp[:, 0].A)[0]
maxStep = 0
alpha_j = 0
error_j = 0
if len(candidateAlphaList) > 1:
for alpha_k in candidateAlphaList:
if alpha_k == alpha_i:
continue
error_k = cal_error(svm, alpha_k)
if abs(error_k - error_i) > maxStep:
maxStep = abs(error_k - error_i)
alpha_j = alpha_k
error_j = error_k
else: # 随机选择
alpha_j = alpha_i
while alpha_j == alpha_i:
alpha_j = int(np.random.uniform(0, svm.n_samples))
error_j = cal_error(svm, alpha_j)
return alpha_j, error_j
def choose_and_update(svm, alpha_i):
'''判断和选择两个alpha进行更新
input: svm:SVM模型
alpha_i(int):选择出的第一个变量
'''
error_i = cal_error(svm, alpha_i) # 计算第一个样本的E_i
# 判断选择出的第一个变量是否违反了KKT条件
if (svm.train_y[alpha_i] * error_i < -svm.toler) and (svm.alphas[alpha_i] < svm.C) or\
(svm.train_y[alpha_i] * error_i > svm.toler) and (svm.alphas[alpha_i] > 0):
# 1、选择第二个变量
alpha_j, error_j = select_second_sample_j(svm, alpha_i, error_i)
alpha_i_old = svm.alphas[alpha_i].copy()
alpha_j_old = svm.alphas[alpha_j].copy()
# 2、计算上下界
if svm.train_y[alpha_i] != svm.train_y[alpha_j]:
L = max(0, svm.alphas[alpha_j] - svm.alphas[alpha_i])
H = min(svm.C, svm.C + svm.alphas[alpha_j] - svm.alphas[alpha_i])
else:
L = max(0, svm.alphas[alpha_j] + svm.alphas[alpha_i] - svm.C)
H = min(svm.C, svm.alphas[alpha_j] + svm.alphas[alpha_i])
if L == H:
return 0
# 3、计算eta
eta = 2.0 * svm.kernel_mat[alpha_i, alpha_j] - svm.kernel_mat[alpha_i, alpha_i] \
- svm.kernel_mat[alpha_j, alpha_j]
if eta >= 0:
return 0
# 4、更新alpha_j
svm.alphas[alpha_j] -= svm.train_y[alpha_j] * (error_i - error_j) / eta
# 5、确定最终的alpha_j
if svm.alphas[alpha_j] > H:
svm.alphas[alpha_j] = H
if svm.alphas[alpha_j] < L:
svm.alphas[alpha_j] = L
# 6、判断是否结束
if abs(alpha_j_old - svm.alphas[alpha_j]) < 0.00001:
update_error_tmp(svm, alpha_j)
return 0
# 7、更新alpha_i
svm.alphas[alpha_i] += svm.train_y[alpha_i] * svm.train_y[alpha_j] \
* (alpha_j_old - svm.alphas[alpha_j])
# 8、更新b
b1 = svm.b - error_i - svm.train_y[alpha_i] * (svm.alphas[alpha_i] - alpha_i_old) \
* svm.kernel_mat[alpha_i, alpha_i] \
- svm.train_y[alpha_j] * (svm.alphas[alpha_j] - alpha_j_old) \
* svm.kernel_mat[alpha_i, alpha_j]
b2 = svm.b - error_j - svm.train_y[alpha_i] * (svm.alphas[alpha_i] - alpha_i_old) \
* svm.kernel_mat[alpha_i, alpha_j] \
- svm.train_y[alpha_j] * (svm.alphas[alpha_j] - alpha_j_old) \
* svm.kernel_mat[alpha_j, alpha_j]
if (0 < svm.alphas[alpha_i]) and (svm.alphas[alpha_i] < svm.C):
svm.b = b1
elif (0 < svm.alphas[alpha_j]) and (svm.alphas[alpha_j] < svm.C):
svm.b = b2
else:
svm.b = (b1 + b2) / 2.0
# 9、更新error
update_error_tmp(svm, alpha_j)
update_error_tmp(svm, alpha_i)
return 1
else:
return 0
def SVM_training(train_x, train_y, C, toler, max_iter, kernel_option = ('rbf', 0.431029)):
'''SVM的训练
input: train_x(mat):训练数据的特征
train_y(mat):训练数据的标签
C(float):惩罚系数
toler(float):迭代的终止条件之一
max_iter(int):最大迭代次数
kerner_option(tuple):核函数的类型及其参数
output: svm模型
'''
# 1、初始化SVM分类器
svm = SVM(train_x, train_y, C, toler, kernel_option)
# 2、开始训练
entireSet = True
alpha_pairs_changed = 0
iteration = 0
while (iteration < max_iter) and ((alpha_pairs_changed > 0) or entireSet):
print("\t iterration: ", iteration)
alpha_pairs_changed = 0
if entireSet:
# 对所有的样本
for x in range(svm.n_samples):
alpha_pairs_changed += choose_and_update(svm, x)
iteration += 1
else:
# 非边界样本
bound_samples = []
for i in range(svm.n_samples):
if svm.alphas[i,0] > 0 and svm.alphas[i,0] < svm.C:
bound_samples.append(i)
for x in bound_samples:
alpha_pairs_changed += choose_and_update(svm, x)
iteration += 1
# 在所有样本和非边界样本之间交替
if entireSet:
entireSet = False
elif alpha_pairs_changed == 0:
entireSet = True
return svm
def svm_predict(svm, test_sample_x):
'''利用SVM模型对每一个样本进行预测
input: svm:SVM模型
test_sample_x(mat):样本
output: predict(float):对样本的预测
'''
# 1、计算核函数矩阵
kernel_value = cal_kernel_value(svm.train_x, test_sample_x, svm.kernel_opt)
# 2、计算预测值
predict = kernel_value.T * np.multiply(svm.train_y, svm.alphas) + svm.b
return predict
def cal_accuracy(svm, test_x, test_y):
'''计算预测的准确性
input: svm:SVM模型
test_x(mat):测试的特征
test_y(mat):测试的标签
output: accuracy(float):预测的准确性
'''
n_samples = np.shape(test_x)[0] # 样本的个数
correct = 0.0
for i in range(n_samples):
# 对每一个样本得到预测值
predict=svm_predict(svm, test_x[i, :])
# 判断每一个样本的预测值与真实值是否一致
if np.sign(predict) == np.sign(test_y[i]):
correct += 1
accuracy = correct / n_samples
return accuracy
def save_svm_model(svm_model, model_file):
'''保存SVM模型
input: svm_model:SVM模型
model_file(string):SVM模型需要保存到的文件
'''
with open(model_file, 'wb') as f:
pickle.dump(svm_model, f)
svm_test.py代码:
# coding:UTF-8
import numpy as np
import pickle
from svm import svm_predict
def load_test_data(test_file):
'''导入测试数据
input: test_file(string):测试数据
output: data(mat):测试样本的特征
'''
data = []
f = open(test_file)
for line in f.readlines():
lines = line.strip().split(' ')
# 处理测试样本中的特征
index = 0
tmp = []
for i in range(0, len(lines)):
li = lines[i].strip().split(":")
if int(li[0]) - 1 == index:
tmp.append(float(li[1]))
else:
while(int(li[0]) - 1 > index):
tmp.append(0)
index += 1
tmp.append(float(li[1]))
index += 1
while len(tmp) < 13:
tmp.append(0)
data.append(tmp)
f.close()
return np.mat(data)
def load_svm_model(svm_model_file):
'''导入SVM模型
input: svm_model_file(string):SVM模型保存的文件
output: svm_model:SVM模型
'''
with open(svm_model_file, 'rb') as f:
svm_model = pickle.load(f)
return svm_model
def get_prediction(test_data, svm):
'''对样本进行预测
input: test_data(mat):测试数据
svm:SVM模型
output: prediction(list):预测所属的类别
'''
m = np.shape(test_data)[0]
prediction = []
for i in range(m):
# 对每一个样本得到预测值
predict = svm_predict(svm, test_data[i, :])
# 得到最终的预测类别
prediction.append(str(np.sign(predict)[0, 0]))
return prediction
def save_prediction(result_file, prediction):
'''保存预测的结果
input: result_file(string):结果保存的文件
prediction(list):预测的结果
'''
f = open(result_file, 'w')
f.write(" ".join(prediction))
f.close()
if __name__ == "__main__":
# 1、导入测试数据
print( "--------- 1.load data ---------")
test_data = load_test_data("svm_test_data")
# 2、导入SVM模型
print("--------- 2.load model ----------")
svm_model = load_svm_model("model_file")
# 3、得到预测值
print("--------- 3.get prediction ---------")
prediction = get_prediction(test_data, svm_model)
# 4、保存最终的预测值
print("--------- 4.save result ----------")
save_prediction("result", prediction)
