数据挖掘-朴素贝叶斯算法的R实现

本次为学生时期所写的实验报告，代码程序为课堂学习和自学，对网络程序有所参考，如有雷同，望指出出处，谢谢！

基础知识来自教材：李航的《统计学习方法》

本人小白，仍在不断学习中，有错误的地方恳请大佬指出，谢谢！

一、实验要求：

编程实现朴素贝叶斯分类器，要求该分类器能够自动处理离散特征和连续特征，验证程序，使用交叉验证评估模型，并与模型KNN算法对比。

二、代码实现（R语言）

1.使用朴素贝叶斯算法计算预测值

naive.bayes.prediction <- function(X,y,condition,continuous = "NO",lambda = 0){
                                    #训练数据集X，y，测试数据condition
#continuous = "NO"表示离散数据，等于"YES"表示连续数据
                                    #默认lambda=1
  
  #公共参数
  yclass = length(unique(y))       #y的类别数
  y = as.matrix(y)                 #将y转化为列向量
  prior = rep(NA,yclass)           #该向量用于存储先验概率的值
  Xfeature = ncol(X)               #X的特征数
  prediction=rep(NA,nrow(condition))
  
  #离散部分参数
  situation <- matrix(NA,nrow = yclass, ncol = Xfeature) 
  #用于存储条件概率的每一个连乘项，其中"列"为X的每个特征，"行"为y的类别.
  above = matrix(NA,nrow = nrow(condition),ncol=yclass)  
  #该向量用于存储贝叶斯分类器公式中分子的值,其中(i,j)元表示给定第i个x下为第j类的概率值的决定值
  
  #连续部分参数
  mu <- matrix(NA,nrow = yclass, ncol = Xfeature) 
  #用于存储给定y的类别下X各特征的平均值，其中行数为y的类别数，列数为X的特征数
  final = matrix(NA,nrow = nrow(condition),ncol = yclass) 
  #该向量用于存储给定x下类别为i的概率值的决定值
  Xscale = scale(X)                     #对X进行标准化，便于协方差矩阵的求解
  sigma = t(Xscale)%*%Xscale            #计算协方差矩阵
  
  
  #离散情况
  if (continuous == "NO"){
    for (i in 1:yclass) {
      #先验概率
      prior[i] <- sum(y == unique(y)[i]) / length(y)  #prior中存储所有y=ck先验概率的值   

      #条件概率
      for (k in 1:nrow(condition)) {
        for (j in 1:Xfeature) {
          situation[i,j] = 
(sum((X[,j]== condition[k,j]) & 
(y[,1] == unique(y)[i]))+lambda)/ 
             (sum(y[,1] == unique(y)[i]) +length(unique(X[,j]))*lambda)
          #situaition的（i,j）元素表示在y = ci条件下Xj = condition中（xj）的条件概率
        }

        #计算条件概率的乘积*先验概率，即贝叶斯分类器公式中分子的值
        above[k,i]=prod(situation[i,])*prior[i]
      }
      
    }
    
    for (k in 1:nrow(condition)) {
      prediction[k] = unique(y)[which.max(above[k,])] 
    }
  }
  
  
  #连续情况  
  else if(continuous == "YES"){
    for (i in 1:yclass) {  
      
      #先验概率
      prior[i] <- sum(y == unique(y)[i]) / length(y)   #prior中存储所有y=ck先验概率的值  

      
      #计算均值
      for (j in 1:Xfeature) {
        mu[i,j] = mean(X[,j][which(y[,1] == unique(y)[i])])  
      }
      
      #计算每个给定x下类别为i的概率值的决定值
      for(k in 1:nrow(condition)){
        final[k,i] = 
log(prior[i])-(1/2)*t(mu[i,])%*%solve(sigma)%*%mu[i,]
+t(condition[k,])%*%solve(sigma)%*%mu[i,]
      }
      
}

    
    for (k in 1:nrow(condition)) {
      prediction[k] = unique(y)[which.max(final[k,])] 
    }
  }
  prediction
}

2.S-折交叉验证函数编写

Stest<- function(X,y,S,judge){    
#S为折数，judge取值为“NO”或“YES”，judge=“NO”时表示数据离散，judge=“YES”时表示数据连续
  
  n = dim(X)[1]   #数据的行数
  percentage = rep(NA,S)
  
  #进行1到S的循环，总长度为n（如1,2,3,4,1,2,3,4,1,2...），并进行打乱
  CV.ID = sample(rep(1:S,length.out = n))  
  for (j in 1:S){
X.test = X[CV.ID==j,]   #相当于从被分为S份的数据中随机抽取1份作为测试数据集，循环S次
           
    y.test = y[CV.ID==j]
X.train = X[CV.ID!=j,]  #相当于从被分为S份的数据中随机抽取（S-1）份作为训练数据集，循环S次

    y.train = y[CV.ID!=j]
    
    y.hat =naive.bayes.prediction(X.train,y.train,X.test,continuous = judge,lambda = 0)     #测试数据集中y的预测值
    
    #由准确率来判断误差大小
    percentage[j] = sum(y.hat==y.test)/length(y.test)
    
  }
  
  correct = mean(percentage)                        #正确率
  error = 1-mean(percentage)                        #误判率
  plot(1:S,percentage,type="l")                     #每一次交叉验证时正确率的折线图
  list(correct = correct,error = error,percentage = percentage
}

三、检验

1.检验数据选择

本次实验使用UCI数据库中Iris数据集：

（1）该数据集的特征量有：萼片长度(Sepal.Length)、萼片宽度(Sepal.Width)、花瓣长度(Petal.Length)、花瓣宽度(Petal.Width)；

（2）类别(Species)有：鸢尾花(Iris Setosa)、鸢尾花(Iris Versicolour)、弗吉尼亚鸢尾 (Iris Virginica)；

（3）不同类别的花所对应的各特征值的数据有所不同。从中抽取部分作为测试数据集，剩下的作为训练数据集，使用贝叶斯算法计算测试数据对应的类，并与实际值进行对比。

2.使用朴素贝叶斯算法进行分类（使用交叉验证法计算每次分类准确率）

输入：

#1.离散数据
#使用chiM算法对UCI数据库的iris数据集进行离散化
library(discretization)
iris <- read.csv("F:/iris.data",header = FALSE)
colnames(iris)=c("Sepal.Length", "Sepal.Width","Petal.Length", "Petal.Width", "Species")
result<-chiM(iris,alpha=0.05)

#离散后的数据为
iris_discrete <- result$Disc.data
X = iris_discrete [,1:4]
X = as.matrix(X)
y = iris_discrete [,5]
y = as.matrix(y)

#进行5-折交叉验证
Stest(X,y,S=5,judge="NO")


#2.连续数据
#使用iris原始数据
iris_continuous <- read.csv("F:/iris.data",header = FALSE)

colnames(iris_continuous)=c("Sepal.Length", "Sepal.Width","Petal.Length", "Petal.Width", "Species")
X = iris_continuous[,1:4]
X = as.matrix(X)
y = iris_continuous[,5]
y = as.matrix(y)

#5-折交叉验证
Stest(X,y,S=5,judge="YES")

输出：

①离散数据：

$correct

[1] 0.9666667

$error

[1] 0.03333333

$percentage

  [1] 1.0000000 0.9000000 0.9333333 1.0000000 1.0000000

分析：由结果可知平均预测准确率为96.67%，五次交叉验证的预测准确率都在90%以上

②连续数据：

> Stest(X,y,S=5,judge="YES")

$correct

[1] 0.8333333

$error

[1] 0.1666667

$percentage

[1] 0.7666667 0.9000000 0.8333333 0.8666667 0.8000000

分析：由结果可知平均预测准确率为83.33%，五次交叉验证的预测准确率集中在76%-90%之间。正确率较高。

四、与knn算法比较

1分析：两种算法的比较考虑实行以下步骤：

  ①设置相同的训练数据集X.train,y.train和测试数据集X.test,y.test

  ②使用朴素贝叶斯算法分类并计算正确率

  ③使用knn算法分类并计算正确率

  ④比较两者正确率大小

*注明1：在文章《数据挖掘-k近邻算法的R实现》可得已验证的knn算法代码以及交叉验证选择最佳k值的代码，在本次实验中将直接使用这两份代码。

*注明2：在文章《数据挖掘-k近邻算法的R实现》中同样使用了UCI的iris数据集，其中使用代码进行交叉验证选择出的最佳k值为5，本实验将沿用此结论。

 2 代码编写

（1）使用交叉验证法选择最佳k值

#使用交叉验证法选择最佳k值
findk <- function(X,y,K.list,S=5){   #S表示交叉验证中的折数（S-折交叉验证）
  nk = length(K.list)
  n = dim(X)[1]   #数据的行数
  CV.ID = sample(rep(1:S,length.out = n))  
                          #进行1到S的循环，总长度为n（如1,2,3,4,1,2,3,4,1,2...），并进行打乱
                        
  CV.per = matrix(NA,nk,S)#交叉验证的下标
  for (i in 1:nk) {
    for (j in 1:S){
      X.test = X[CV.ID==j,] #相当于从被分为S份的数据中随机抽取1份作为测试数据集，循环S次

      y.test = y[CV.ID==j]
      X.train = X[CV.ID!=j,]#相当于从被分为S份的数据中随机抽取（S-1）份作为训练数据集，循环S次

      y.train = y[CV.ID!=j]

      y.hat =myknn(X.train, y.train, X.test,K = K.list[i], distance = 'euclidean')  
                                     #测试数据集中y的预测值
      y.test = as.numeric(y.test)
      y.hat = as.numeric(y.hat)      #将向量转化为数值型
      
      CV.per[i,j] = mean((y.test-y.hat)^2)
    }
  }
  CV.per.mean = apply(CV.per, 1, mean) #将各K值对应的交叉验证误差存储在此向量中

  plot(K.list,CV.per.mean,type="l") #绘制k值与对应误差值的函数图，可用于直观判断k值的最佳取值

  K.opt = K.list[which.min(CV.per.mean)]
  list(CV.per=CV.per, CV.per.mean=CV.per.mean, K.opt=K.opt)
}

（2）在上一篇文章中已知knn算法程序：

myknn <- function(train.data, ytrain, test.data, K=3, distance = 'euclidean'){ 
  #输入训练数据集和测试数据集数据，默认给定k值为3，默认距离函数使用欧氏距离
  testlen = nrow(test.data)   #测试数据集的行数
  trainlen = nrow(train.data) #训练数据集的行数
  
  A = rbind(test.data,train.data) #A为测试数据集和训练数据集按行合并形成的矩阵
  
  dist = dist(A,method = distance)
  testdist = as.matrix(dist)[1:testlen,(testlen+1):(testlen+trainlen)]       
  #将dist变换为矩阵形式，并取适当的行和列，使得第（i，j）元素为测试数据集第i行向量与训练数据集第j行向量的距离
  
  colnames(testdist) = c(1:trainlen)  #更改列编号为从1开始
  
  ytest = rep(NA,testlen)  #建立长度与测试数据集等长的空向量，用于存储测试数据集对应的y的预测值

  for (i in 1:testlen) {
testsorted = sort(testdist[i,],index.return = TRUE)  
                             #将距离矩阵的第i行按从小到大排列，并返回排序后对应于原序列的下标

reindex = testsorted$ix[1:K]  
                             #返回与第i行测试数据距离最近的前K个训练数据对应的原下标
    
    #接下来寻找下标对应的y值中出现频率最大的y值
    uniqve = unique(ytrain[reindex])        #去掉下标对应的y值中重复的值
    match = match(ytrain[reindex],uniqve)     

   #找出ytrain[reindex]中每个元素在uniqve中的位置
    tabulate = tabulate(match)       #记录match从1开始的数字中各数字出现的次数
    max = which.max(tabulate)         #找出tabulate中最大的数
    
    ytest[i]=uniqve[max] 
  }
  
  ytest
}

（3）编写比较函数

compare <- function(X,y,S=5){
  
  n = dim(X)[1]   #数据的行数
  percentage =matrix(NA,ncol = 2,nrow = S)
  
  #进行1到S的循环，总长度为n（如1,2,3,4,1,2,3,4,1,2...），并进行打乱
  CV.ID = sample(rep(1:S,length.out = n))  
  for (j in 1:S){
X.test = X[CV.ID==j,]  #相当于从被分为S份的数据中随机抽取1份作为测试数据集，循环S次

    y.test = y[CV.ID==j]
X.train = X[CV.ID!=j,]  #相当于从被分为S份的数据中随机抽取（S-1）份作为训练数据集，循环S次

    y.train = y[CV.ID!=j]
    
yhat_bayes = naive.bayes.prediction(X.train,y.train,
X.test,continuous = "YES")  #计算贝叶斯算法下测试数据集中y的预测值


yhat_knn = myknn(X.train,y.train,X.test,K=5,
distance = "euclidean")   #计算knn算法下测试数据集中y的预测值（已知最佳k值为5）

    
    #计算准确率
    percentage[j,1] = sum(yhat_bayes==y.test)/length(y.test)
    percentage[j,2] = sum(yhat_knn==y.test)/length(y.test)
  }
  
  correct = apply(percentage,2,mean)  #分别求每列的均值
  
par(mfrow = c(1,2))
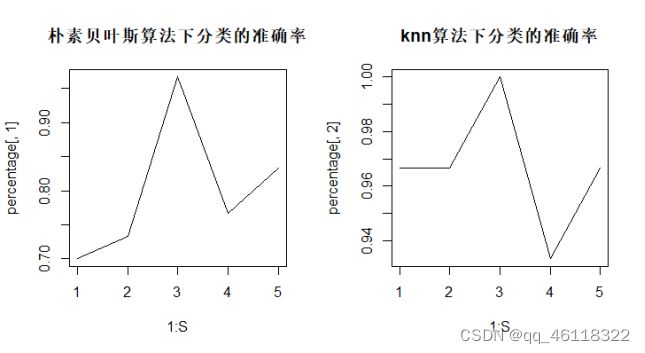
  plot(1:S,percentage[,1],type="l",main = "朴素贝叶斯算法下分类的准确率")
  plot(1:S,percentage[,2],type="l",main = "knn算法下分类的准确率")  
  list(correct = correct,percentage = percentage)
  
}

compare(X,y,S=5)

3.输出

$correct

[1] 0.8000000 0.9666667

$percentage

          [,1]      [,2]

[1,] 0.7000000 0.9666667

[2,] 0.7333333 0.9666667

[3,] 0.9666667 1.0000000

[4,] 0.7666667 0.9333333

[5,] 0.8333333 0.9666667

分析：由结果得(针对连续变量iris)朴素贝叶斯算法的平均准确率为80%，knn算法的平均准确率为96.7%。在5个交叉验证中朴素贝叶斯算法分类准确率也均低于knn算法。可知knn算法预测效果较好。由图像可看出两者每一次交叉验证所使用数据集下预测值的起伏情况大致一致。

五、小结

本次实验主要编写了朴素贝叶斯算法（离散数据和连续数据）的程序，并使用了交叉验证法验证算法程序正确与否。这个过程要求我们熟练掌握朴素贝叶斯分类的基本过程。先验概率的计算较为简单（使用频率估计概率），难点在于条件概率的计算过程。我们需明确给定y下X个特征独立同分布的重要假定。在具体计算方面：对于离散情况，条件概率由各x特征值概率的乘积估计而来；而对于连续情况，则需要根据假定的给定y下X的多元概率分布密度函数来计算（本实验中假定X服从多元正态分布）,最后取使得后验概率最大的k即为所求的类别ck。同时也需及时复习先前学习的其他算法。对于同一数据，不同算法的预测准确率可能有着较大的不同，这将帮助我们选择更好的算法进行数据预测。