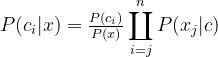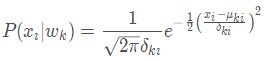【机器学习】贝叶斯分类器与朴素贝叶斯

目录

贝叶斯分类器

朴素贝叶斯分类器

朴素贝叶斯分类器应用

参考

---

贝叶斯分类器

在介绍贝叶斯分类器之前，首先需要知道先验概率、后验概率以及全概率的相关概念及计算公式，这里不再赘述。

（1）贝叶斯公式的一般形式

                                                                               

 这个公式用于计算A发生情况下，B发生的概率，往往A是结果，B是可能导致这一结果的某一因素。

（2）对于分类问题的贝叶斯公式

我们可以将上述一般形式下的贝叶斯公式看成如下：

                                                                               

假设有待分类的k个类别：，特征属性值有n维:，那么上面的式子可以继续改写为：

                                                                                    

也就是在已知特征属性x条件下，分别计算出样本属于第i个类别的概率，即求后验概率P(c|x)。公式中，为类先验概率，表示第i个类别的样本数量占总样本数量的个数。表示类条件概率，也叫"似然"，是用于归一化的证据因子(想想也知道它对于每个类都是不变的，因此忽略它)

之后，我们基于最大后验概率原则可以预测样本是属于哪一类的:

                                                                                     

由于归一化因子对于每一类都是不变的，因此主要在于计算类条件概率：

                                                                                                    

（3）例题分析

西瓜的状态分为两种：好瓜与坏瓜，概率分别为0.6和0.4，并且好瓜里面纹理清晰的概率是0.8，坏瓜里面纹理清晰的概率是0.4。那么，我现在挑了一个纹理清晰的瓜，该瓜是好瓜的概率是多少？

很明显，这是一个后验概率问题，我们可以直接给出公式：

对公式里面出现的概率一个一个分析：

后验概率：P（纹理清晰|好瓜）=0.8

先验概率：P（好瓜）=0.6

后验概率：P（纹理清晰|坏瓜）=0.4

先验概率：P（坏瓜）=0.4

由上面分析的数值，我们可以直接求解上式：

 

这样，我们就计算得到了纹理清晰的情况下好瓜的概率是0.75。上面计算后验概率P（好瓜|纹理清晰）的公式就是利用了贝叶斯定理。

在上面的例题中类条件概率P(x|c)是直接给出来的，但是实际上它涉及x所有属性的联合概率，直接根据样本出现的频率来估计将会遇到严重的困难。例如如果每个样本有有d个属性，每个属性都是二值的，那么所有的可能性为2^d种，一般情况下，我们的训练集覆盖不了全部的可能性，因此直接使用频率来估计P(x|c)显然不可行。为此引出了朴素贝叶斯。

朴素贝叶斯分类器

（1）计算公式

朴素贝叶斯分类器的原理是采用属性条件独立性假设，即假设所有属性相互独立，每个属性独立对分类结果产生影响。因此有：

                                                                                

 进一步地将贝叶斯公式改写为：

                                                                                  

i表示第i个类别，表示样本的第j个特征（属性），之后求解后验概率最大值：

                                                                

计算问题：

• 离散型随机变量

        记的样本总数为N，在中出现的次数为n，则

• 连续型随机变量

        假设服从正态分布（wk等于ci）

     其中，是第k类第i维的标准差，是第k类第i维的均值。

（2）例题分析

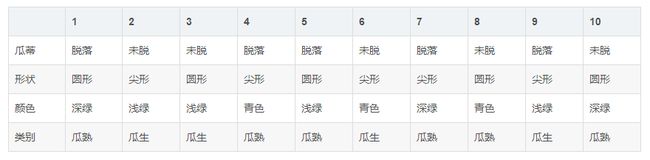
这组数据是不同瓜蒂、形状、颜色对应的西瓜是生是熟。

其中，瓜蒂分为脱落和未脱，形状分为圆形和尖形，颜色分为深绿、浅绿、青色。不同特征组合对应着瓜熟或者瓜生。现在，挑了一个西瓜，它的瓜蒂脱落、形状圆形、颜色青色，请问这个瓜是熟的还是生的？

• 首先，对于瓜熟的情况：

        类先验概率： P(瓜熟) = 6 / 10 = 0.6。

        类条件概率： P(脱落 | 瓜熟) = 4 / 6 = 2 / 3。

        类条件概率： P(圆形 | 瓜熟) = 4 / 6 = 2 / 3。

        类条件概率： P(青色 | 瓜熟) = 2 / 6 = 1 / 3。

        计算后验概率分子部分：

        P(瓜熟) × P(脱落 | 瓜熟) × P(圆形 | 瓜熟) × P(青色 | 瓜熟) = 0.6 × (2 / 3) × (2 / 3) × (1 / 3) = 4 / 45。

• 然后，对于瓜生的情况：

       类先验概率： P(瓜生) = 4 / 10 = 0.4。

       类条件概率： P(脱落 | 瓜生) = 1 / 4 = 0.25。

       类条件概率： P(圆形 | 瓜生) = 1 / 4 = 0.25。

       类条件概率： P(青色 | 瓜生) = 1 / 4 = 0.25。

       计算后验概率分子部分：

       P(瓜生) × P(脱落 | 瓜生) × P(圆形 | 瓜生) × P(青色 | 瓜生) = 0.4 × 0.25 × 0.25 × 0.25 = 1 / 160。

       因为 4 / 45 > 1 / 160，所以预测为瓜熟。终于计算完了，红色石头很肯定地说这个西瓜瓜蒂脱落、形状圆形、颜色青色，应该是熟瓜。

朴素贝叶斯分类器应用

（1）垃圾邮件过滤

 通过比较P(h+|D)和P(h-|D)的大小就可以知道属于正常邮件还是垃圾邮件。

 

（2）拼写纠正

给定一个单词w，任务是选择和它最相似的拼写正确的单词c. (如果这个单词本身拼写就是正确的, 那么最相近的就是它自己). 也就是求argmaxc P(c|w)，即在用户输入w的情况下，枚举所有可能的c，那个在输入w情况下概率最大的c就可能是真正用户想要的输入的正确单词。根据贝叶斯公式上面的式子等价于 argmax P(w|c) P(c) / P(w)，因此对于任何 c 来讲,P(w) 都是一样的即重点在于求：

                                                                                        

其中:

• P(c)，文章中出现一个正确拼写词 c 的概率, 也就是说, 在英语文章中, c 出现的概率有多大呢? 因为这个概率完全由英语这种语言决定, 我们称之为做语言模型. 好比说, 英语中出现 the 的概率  P('the') 就相对高, 而出现  P('zxzxzxzyy') 的概率接近0(假设后者也是一个词的话).
• P(w|c), 在用户想键入 c 的情况下敲成 w 的概率. 因为这个是代表用户会以多大的概率把 c 敲错成 w, 因此被称为误 差模型.

具体的计算步骤见博客：利用朴素贝叶斯实现拼写纠错器

参考

贝叶斯分类器

贝叶斯分类器解读

贝叶斯分类器推导过程

通俗易懂！白话朴素贝叶斯