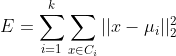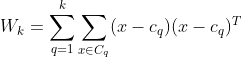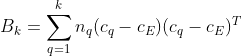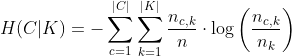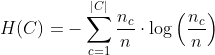机器学习笔记（七）聚类算法K-means原理和实践

在机器学习领域，除以LR、DT、SVM等为代表的有监督算法外，还有另外一类特殊的存在——无监督算法，其中最为经典就是聚类算法了。聚类算法因为其不需要先验标签，因此在很多领域应用都较为广泛。聚类算法主要有：K-means、DBSCAN、Birch、Spectral clustering、OPTICS等，在本篇文章以及接下来的几篇文章中我们会依次介绍这些算法。

1. K-means原理

K-means的实现比较简单，聚类效果也不错，因此应用比较广泛。对于给定的样本集，K-means按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。如果用数据表达式表示，假设簇划分为  则我们的目标是最小化平方误差E，其实E就是欧氏距离：

                                                                  

其中  是簇  的均值向量，有时也称为质心，表达式为：

                                                                  

当然这里的E的计算并不局限于欧氏距离，也可以使用绝对值距离、余弦距离、明氏距离等。根据E的表达式可以发现，k-means是对特征尺度敏感的，所以在聚类之前，需要先对所有特征进行归一化。这也意味着我们可以通过为特征添加不同的系数，间接调整特征的权重。

如果我们想直接求上式的最小值并不容易，这是一个NP难的问题，因此只能采用启发式的迭代方法。不过K-Means采用的启发式方法很简单，其过程可描述为：① 在所有样本集中选择K个初始中心点；② 对剩下的所有样本点计算到K个中心点的距离，并将自己标识为和距离自己最近的中心点同一个类别；③ 对得到的K个簇，重新计算每个簇的中心点（质心），也就是簇  中所有样本的均值向量；④ 基于新的中心点，再次把每个样本重新标识为和自己最近的中心点一样的类别，也就得到了新的K个簇；⑤ 依次重复③和④直到所有的中心点不再变化。过程如下图：

数字化的描述流程如下：

1. 输入样本集D={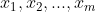}，聚类的簇数为 K，分别为 C={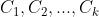}，且每个簇都为空集，最大迭代次数N
2. 从数据集D中随机选择k个样本作为初始的k个质心向量：
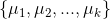
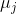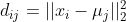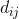3.  对于i=1,2...m,计算样本  和各个质心向量  (j=1,2,...k) 之间的距离：，将  标记为  最小的 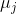 所对应的类别 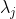。此时更新 
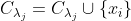
4. 对任意簇 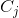 ，( j=1,2,...,k ) 中所有的样本点重新计算新的质心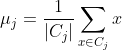
5. 重复步骤3和4，直到所有的中心点  都不再变化，输出最终的聚类结果 C={}

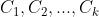2. K-means++

上一节我们介绍了K-means的原理，但是这里有一个问题就是初始中心点的选择会对迭代效率和迭代效果产生很大的影响，如果初始中心点很近，那必然要多轮迭代才能完成聚类过程。另外，下图的两个簇，如果样本点分布是对称的，初始中心点的选择刚好也是对称的，那么聚类的结果很可能是上下两个分布各有一半属于一个簇，结果显然不合理。

针对这个问题，K-means++算法就对K-means初始化质心的随机选择方法进行了优化。优化策略也很简单，如下：

1.  从输入的数据点集合中随机选择一个点作为第一个聚类中心 
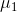
2.  对于数据集中的每一个点 ，计算它与已选择的聚类中心中最近聚类中心的距离 
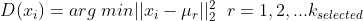
3. 选择一个新的数据点作为新的聚类中心，选择的原则是：D(x) 较大的点，被选取作为聚类中心的概率较大
4. 重复2和3直到选择出k个聚类质心，利用这k个质心作为初始化质心去运行标准的K-Means算法

sklearn也提供了kmeans++的API sklearn.cluster.kmeans_plusplus供调用。另外，也有使用 PCA 降维算法选择初始质心的尝试。

3. elkan K-means

在传统的K-Means算法中，我们在每轮迭代时，要计算所有的样本点到所有的质心的距离，这样会比较的耗时。那么，对于距离的计算有没有能够简化的地方呢？elkan K-Means算法就是从这块入手加以改进。它的目标是减少不必要的距离计算。那么哪些距离不需要计算呢？elkan K-Means利用了三角形的两个定律：两边之和大于等于第三边；两边之差小于第三边，减少距离的计算。

对于一个样本点x和两个质心 。如果我们预先计算出了这两个质心之间的距离 ，如果计算发现2D(x,)≤，我们立即就可以知道D(x,)≤D(x,)。此时我们不需要再计算 ，省了一步距离计算。对于第二个定律，如果已知 ， ，则显然 ，此时若已知 ，则就不用计算了。

4. Mini Batch K-means

在K-Means算法中，要计算所有样本点到所有质心的距离。如果样本量非常大，比如达到10万以上，而特征也很多，如100以上，此时用K-Means算法就会非常的耗时，就算加上elkan K-Means优化也依旧。此时Mini Batch K-Means算法应运而生。

顾名思义，Mini Batch，也就是用样本集中的一部分的样本来做K-Means，这样可以避免样本量太大时的计算难题，算法收敛速度大大加快。当然此时的代价就是我们的聚类的精确度也会有一些降低。一般来说这个降低的幅度在可接受的范围内。

在Mini Batch K-Means中，我们会选择一个合适的批样本大小batch size，我们仅仅用batch size个样本来做K-Means聚类。那么这batch size个样本怎么来的？一般是通过无放回的随机采样得到的。即选择batch size个样本，把这batch size个样本更新到距离自己最近的中心点，然后更新每个簇的中心向量，然后继续下一个batch size样本。为了增加算法的准确性，我们一般会多跑几次Mini Batch K-Means算法，用得到不同的随机采样集来得到聚类簇，选择其中最优的聚类簇。

5. 优缺点

K-Means是个简单实用的聚类算法，这里对K-Means的优缺点做一个总结。

K-Means的主要优点有：

1. 原理简单，实现容易，收敛速度快。
2. 聚类效果较优。
3. 算法的可解释度比较强。
4. 主要需要调参的参数仅仅是簇数k。

K-Means的主要缺点有：

1. K值的选取不好把握，因为通常情况下，我们对簇类结果树是未知的，需要不断尝试迭代
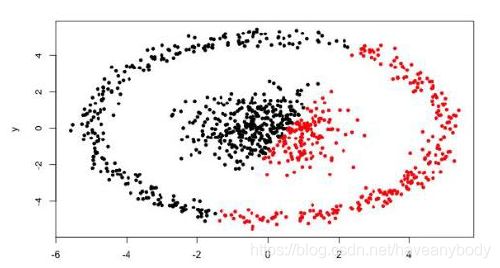
2. 对于不是凸的数据集比较难收敛，很难发现任意形状的簇，例如下面的图
3. 如果各隐含类别的数据不平衡，比如各隐含类别的数据量严重失衡，或者各隐含类别的方差不同，则聚类效果不佳
4. 采用迭代方法，得到的结果只是局部最优
5.  对噪音和异常点比较的敏感，尤其是离群点会影响类中心的计算。
6. 算法不稳定，尤其是受初始中心点的选择影响较大，在复现的时候可能会存在前后不一致的情况。因此，在实际中建议多运行几次比较效果。一个显著的问题信号是，如果多次运行K均值的结果都有很大差异，那么有很高的概率K均值不适合当前数据，要对结果谨慎的分析。

 

6. 特征的特殊处理

聚类算法是对特征比较敏感的算法，尤其是无效特征很可能会把结果引导向一个不好的方向，因此聚类前的特征筛选和处理就显得异常重要。

6.1 特征处理

（1）在第一节中我们就提到了，k-means需要做归一化处理。但是对于枚举型变量，如果我们直接做one-hot处理（取值为0或1），就会导致该类型特征变强，可能会出现超级大簇现象，或者削弱其他特征的表达。那么我们在聚完类后，可以将聚类结果和枚举数据做交叉分析，判断是否是该类特征导致的。如果是，可以适当降低该类特征的权重。

（2）有些数据分布呈现长尾分布现象，例如80%的数据分布在1%的空间内，而剩下的20%的数据分布在99%的空间内。聚类时，分布在1%空间内的大部分数据会被聚为一类，剩下的聚为一类。当不断增加K值时，模型一般是对99%空间内的数据不断进行细分，因为这些数据之间的空间距离比较大。而对分布在1%空间内的数据则很难进一步细分，或者即使细分了，也只是剥离出了外侧少量数据。此时，如果发现是某些特征导致了此现象，可以对特征进行对数处理。

（3）对于（2）中提到的长尾现象，除了特征层面做处理外，还需要考虑数据分布问题，尤其是某些业务场景正样本的获取是很难的，以至于在业务层面数据分布本就是不平衡的，此时也可以考虑对大簇进行下采样处理，即丢弃一部分样本。

（4）在遇到训练数据过于庞大，无法完成训练任务或者学习时间过长时，也可以考虑通过采样方法，在小批量数据集上进行测试，实验多种算法，并最终融合结果。但是采样不均衡、采样规模不容易把握等原因，也会影响聚类结果。因此，当数据量非常大时，可以优先试试 k-means 聚类，得到初步的结果。如果效果不好，再通过随机采样的方法构建更多小样本，手动融合模型提升聚类结果，进一步优化模型。在采样过程中也需要注意[6]：

• 随机采样的样本大小很重要，也不能过小。需要足够的代表性，即小样本依然可以代表总体的数据分布。如果最终需要划分很多个簇，那么要非常小心，因为小样本可能无法体现体量很小的簇。
• 在融合过程中要关注样本上的聚类结果是否稳定，随机性是否过大。要特别注意不同样本上的簇标号是否统一，如何证明不同样本上的簇结果是一致的。

对于其他特殊现象，在聚类时，除了考虑更换算法和调参外，更要注意特征工程的处理，因为相比其他模型，聚类模型对特征更加敏感。

6.2 特征选择

本节内容节选自知乎大神微调的回答[6]。

（1）聚类分析时需要使用什么变量（特征）

这个是一个非常难回答的问题，而且充满了迷惑性，不少人都做错了。举个简单的例子，我们现在有很多客户的商品购买信息，以及他们的个人信息，是否该用购买信息+个人信息来进行聚类呢？未必，我们需要首先回答最重要的一个问题：我们要解决什么问题？如果我们用个人信息，如性别、年龄进行聚类，那么结果会被这些变量所影响，而变成了对性别和年龄的聚类。所以我们应该先问自己，“客户购物习惯”更重要还是“客户的个人信息”更重要？如果我们最在意的是客户怎么花钱，以及购物特征，那就应该完全排除客户的个人信息（如年龄性别家庭住址），仅使用购买相关的数据进行聚类。这样的聚类结果才是完全由购买情况所驱动的，而不会受到用户个人信息的影响。那该如何更好的利用客户的个人信息呢？这个应该被用在聚类之后。当我们得到聚类结果后，可以对每个簇进行分析，分析簇中用户的个人情况，比如高净值客户的平均年龄、居住区域、开什么车。无关变量不应该作为输入，而应该得到聚类结果后作为分析变量。

一般情况下，我们先要问自己，这个项目在意的是什么？很多时候个人信息被错误的使用在了聚类当中，聚类结果完全由个人信息所决定（比如男性和女性被分到了两个簇中），对于商业决策的意义就不大了。一般来说，应该由商业数据驱动，得到聚类结果后再对每个簇中的用户个人信息进行整合分析。但值得注意的是，这个方法不是绝对的。在聚类中有时候也会适当引入个人信息，也可以通过调整不同变量的权重来调整每个变量的影响，即6.1节（1）中介绍的方法。

（2）如何分析变量的重要性

首先变量选择是主观的，完全依赖于建模者对于问题的理解，而且往往都是想到什么用什么。因为聚类是无监督学习，因此很难评估变量的重要性。介绍两种思考方法：

• 考虑变量的内在变化度与变量间的关联性：一个变量本身方差很小，那么不易对聚类起到很大的影响。如果变量间的相关性很高，那么高相关性间的变量应该被合并处理
• 直接采用算法来对变量重要性进行排序：比如 Principal Feature Analysis，网上有现成的代码

另一个鸡生蛋蛋生鸡的问题是，如果我用算法找到了重要特征，那么仅用重要特征建模可以吗？这个依然不好说，我觉得最需要去除的是高相关性的变量，因为很多聚类算法无法识别高相关性，会重复计算高相关性特征，并夸大了其影响，比如K均值。

7. 聚类评价标准

聚类算法多用在无监督场景，不像众多有监督算法一样，可以选择Recall、F1、AUC等指标来衡量模型效果，不过也有一些指标可以用来衡量聚类的好坏程度。下面所列的指标都可以在sklearn官网（scikit-learn 0.24.0）查看，。

7.1 无监督评价

无监督评价又叫内部指标，指标不需要知道样本所属的实际类别。因为聚类算法多用在样本标签未知的场景，所以内部指标的应用比较广泛。

（1）轮廓系数 Silhouette Coefficient

定义a：一个样本与同一簇类中的其他样本点的平均距离；

定义b：一个样本与距离最近簇类中所有样本点的平均距离；

则每个样本的轮廓系数定义为：

                                                                  

一组数据集的轮廓系数等于该数据集中每一个样本轮廓系数的平均值。

from sklearn import metrics
from sklearn.metrics import pairwise_distances
from sklearn import datasets
import numpy as np
from sklearn.cluster import KMeans

X, y = datasets.load_iris(return_X_y=True)
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans_model.labels_
metrics.silhouette_score(X, labels, metric='euclidean')

0.5528190123564091

轮廓系数处于[-1,1]的范围内，-1表示错误的聚类，1表示高密度的聚类，0附近表示重叠的聚类。对于凸面聚类而言，轮廓系数通常比其他聚类概念要高，例如通过DBSCAN获得的基于密度的聚类。

（2）Calinski-Harabasz Index

Caliniski-Harabaz指数评价聚类模型好的标准：同一簇类的数据集尽可能密集，不同簇类的数据集尽可能远离。

对于一组规模为  的数据集 E，聚类成k个簇，我们定义Calinski-Harabasz score 为簇间离散均值与簇内离散度的比值，定义如下：

                                                                 

其中tr(Bk)为簇间离散矩阵的迹，tr(Wk)为簇内离散矩阵的迹，定义如下:

                                                                

                                                               

其中  为簇 q 中的样本集合， 为簇 q 的中心， 为 E 的中心， 为簇 q 中的样本数。根据协方差的相关概念，我们用簇内离散度矩阵的迹表示同一簇类的密集程度，迹越小，同一簇类的数据集越密集（方差越小）；簇间离散度矩阵的迹表示不同簇间的远离程度，迹越大，不同簇间的远离程度越大（方差越大），所以当簇内密集且簇间分离较好时，Caliniski-Harabaz分数越高，聚类性能越好。因为计算简单，Caliniski-Harabaz的计算一般比较快，应用也比较多。不过要注意，凸簇的Caliniski-Harabaz值一般要高于其它类型，例如通过DBSCAN获得的基于密度的簇。

在实际使用中，Silhouette Coefficient 和 Calinski-Harabasz Index 是使用比较多的指标，一般 Silhouette Coefficient 的效果会更好，但是计算比较耗时间，在大数据量情况下建议使用 Calinski-Harabasz Index。

from sklearn import metrics
from sklearn.metrics import pairwise_distances
from sklearn import datasets
import numpy as np
from sklearn.cluster import KMeans

X, y = datasets.load_iris(return_X_y=True)
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans_model.labels_
metrics.calinski_harabasz_score(X, labels)

561.62775662962

（3）Davies-Bouldin Index

定义  表示簇 i 和簇 j 之间的相似度：

                                                                 

 表示簇 i 内每个样本和簇心之间的平均距离， 表示簇 i 和簇 j 之间的簇心距离。则 Davies-Bouldin 指数为：

                                                                 

凸簇的DB指数同样比其他类型的簇高，比如通过DBSCAN获得的基于密度的簇。簇类中心的距离度量限制在欧式空间。

from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn.metrics import davies_bouldin_score

iris = datasets.load_iris()
X = iris.data
kmeans = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans.labels_
davies_bouldin_score(X, labels)

0.6619715465007528

（4）手肘法

手肘法也是一个使用比较广泛的 k 选择指标，网上对该方法的介绍资料相对也比较多，这里主要介绍一下其原理和计算方法。 

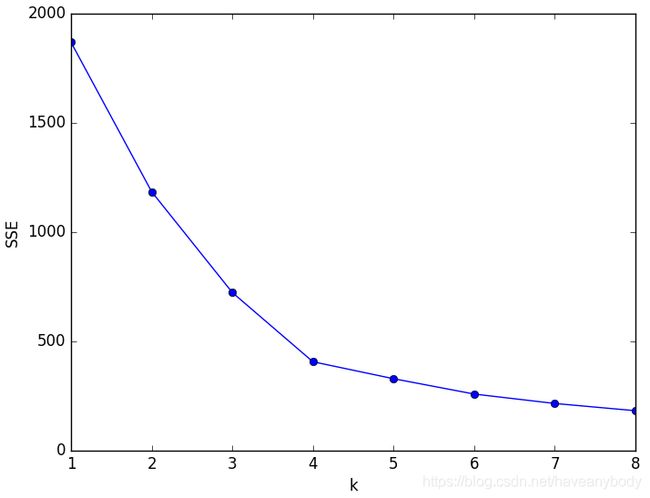
我们知道k-means是以最小化样本与质心的平方误差作为目标函数，将每个簇的质心与簇内样本点的平方距离误差和称为畸变程度(distortions)。那么，对于一个簇，它的畸变程度越低，代表簇内成员越紧密，畸变程度越高，代表簇内结构越松散。 畸变程度会随着类别的增加而降低，但对于有一定区分度的数据，在达到某个临界点时畸变程度会得到极大改善，之后再增加类别数 k 畸变程度的下降就会变得相对缓慢，这个临界点就可以考虑作为聚类性能较好的 k 选择点。 基于这个指标，我们可以重复训练多个k-means模型，选取不同的k值，来得到相对合适的聚类类别。手肘法的核心指标是SSE(sum of the squared errors，误差平方和)：

                                                                 

其中，i 表示第 i 个簇，p 是簇  的样本点， 是簇  的质心，SSE 是所有样本的聚类误差。

下图是一个聚类实例 k-SSE 图，可以发现在 k < 4 的时候，SSE下降较快，在 k > 4 以后，SSE下降较慢，因此可以选择 k=4 作为聚类簇数。在计算SSE值的时候，同样需要多次运行几次测试。

sklearn的metrics库中虽然没有提供SSE的API，但是k-means提供了 inertia_ 属性，可以获得所有样本点到它们簇中心的距离平方和，其实就是SSE。

7.2 有监督评价

有监督评价指标也叫外部指标，需要知道样本所属的实际类别，这里要区别于有监督算法，只是在评价阶段需要label，学习阶段还是聚类算法，不需要标签的。因为需要知道真实标签，所以有监督评价用的并不多。

（1）兰德系数 RI

已知下面的数据结果，第一行是聚类结果，第二行是实际类别标签。对于聚类算法，类别标签的大小是没有意义的，只是为了区分不同的簇而已，所以不需要聚类label和实际label一一对应，实际上也无法对应。

定义 a 表示聚类类别和实际类别一样的样本对个数。例如上面的红框部分，在聚类中是同一个簇，在实际label中也属于同一个类别，所以 a = 2。定义 b 表示聚类类别和实际类别不一样的样本对个数。例如上面的绿框标识的样本对，所以 b=8。定义C为样本数。则定义兰德系数为：

                                                                 

其中  表示组合数，RI的取值范围为[0,1]，越大表示越相似。

from sklearn import metrics

labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
print(metrics.rand_score(labels_true, labels_pred))          ## RI
print(metrics.adjusted_rand_score(labels_true, labels_pred)) ## ARI

0.6666666666666666
0.24242424242424243

（2）调整兰德系数 ARI

RI系数的缺点是随着聚类数的增加，随机分配簇类向量的RI也逐渐增加，这是不符合理论的，随机分配簇类标记向量的RI应为0。ARI解决了RI不能很好的描述随机分配簇类标记向量的相似度问题，ARI的定义：

                                                               

其中E表示期望，max表示取最大值。具体计算方法可参考文献[4]或者维基百科。ARI的取值范围为[-1,1]，ARI越大表示预测簇向量和真实簇向量相似度越高，ARI接近于0表示簇向量是随机分配，ARI为负数表示效果非常差。从广义的角度来讲，ARI衡量的是两个数据分布的吻合程度。

（3）互信息 MI

MI也有相应的调整的互信息指数（AMI）和标准化的互信息指数（NMI），具体就算方法可参考sklearn官网。

from sklearn import metrics

labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]

print(metrics.mutual_info_score(labels_true, labels_pred))            ## MI
print(metrics.adjusted_mutual_info_score(labels_true, labels_pred))   ## AMI
print(metrics.normalized_mutual_info_score(labels_true, labels_pred)) ## NMI

0.4620981203732969
0.29879245817089006
0.5158037429793889

（4）同质性，完整性和V-measure

同质性（homogeneity）：衡量每个簇只包含单个类成员；

                                                               

完整性（completeness）：衡量某个类的所有成员分配给同一簇类；

                                                               

其中H(C|K)为给定簇分配的类的条件熵，计算方法为:

                                                               

H(C)是各类别的熵：

                                                               

n 表示样本总数， 和  分别表示属于类c和类k的样本个数，最后  表示属于类c的样本个数，归到类k的样本个数。

V-meansure是同质性和完整性的调和平均：

                                                               

 默认值是1，如果小于1，同质性将赋予更多权重，如果使用大于1的值，完整性将赋予更多权重。存在关系：homogeneity_score(a, b) == completeness_score(b, a)

from sklearn import metrics

labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]

print(metrics.homogeneity_score(labels_true, labels_pred))
print(metrics.completeness_score(labels_true, labels_pred))
print(metrics.v_measure_score(labels_true, labels_pred))
print(metrics.homogeneity_completeness_v_measure(labels_true,labels_pred))

0.6666666666666669
0.420619835714305
0.5158037429793889
(0.6666666666666669, 0.420619835714305, 0.5158037429793889)

0表示相似度最低，1表示相似度最高，分数与相似度成正相关的关系。

（5）Fowlkes-Mallows

Fowlkes-Mallows指数（FMI）是成对准确率和召回率的几何平均值：

                                                               

其中TP是真正例（True Positive），即真实标签和预测标签属于相同簇类的样本对个数；FP是假正例（False Positive），即真实标签属于同一簇类，相应的预测标签不属于该簇类的样本对个数；FN是假负例（False Negative），即预测标签属于同一簇类，相应的真实标签不属于该簇类的样本对个数。

from sklearn import metrics

labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
print(metrics.fowlkes_mallows_score(labels_true, labels_pred))

0.4714045207910317

FMI范围为[0,1]，值接近于0表示随机分配的标签在很大程度上是相互独立的，接近于1表示一致的簇向量。

（6）Contingency Matrix

Contingency Matrix（列联矩阵）用于输出预测值和实际标签的交集对数，类似于混淆矩阵，好处是可以看到每个类别的分布情况，不足是当数据量大的时候不直观，没有一个统一的指标来衡量效果。

from sklearn.metrics.cluster import contingency_matrix

x = ["a", "a", "a", "b", "b", "b"]
y = [0, 0, 1, 1, 2, 2]
contingency_matrix(x, y)

array([[2, 1, 0],
       [0, 1, 2]])

上面例子的输出矩阵是2行3列，表示实际类别是两个，聚类结果是三类。矩阵的第一行表示类别 “a” 有两个在簇0中，1个在簇1中，没有在簇2的；第二行表示类别“b”没有在簇0的，1个在簇1，两个在簇2。

（7）Pair Confusion Matrix

from sklearn.metrics.cluster import pair_confusion_matrix

pair_confusion_matrix([0, 0, 1, 2], [0, 0, 1, 1])

array([[8, 2],
       [0, 2]])

Pair Confusion Matrix的计算实际利用了Contingency Matrix的结果：

labels_true, labels_pred = check_clusterings(labels_true, labels_pred)
n_samples = np.int64(labels_true.shape[0])

# Computation using the contingency data，结果为稀疏矩阵
contingency = contingency_matrix(
    labels_true, labels_pred, sparse=True, dtype=np.int64
)
n_c = np.ravel(contingency.sum(axis=1))
n_k = np.ravel(contingency.sum(axis=0))
sum_squares = (contingency.data ** 2).sum()
C = np.empty((2, 2), dtype=np.int64)
C[1, 1] = sum_squares - n_samples
C[0, 1] = contingency.dot(n_k).sum() - sum_squares
C[1, 0] = contingency.transpose().dot(n_c).sum() - sum_squares
C[0, 0] = n_samples ** 2 - C[0, 1] - C[1, 0] - sum_squares

7.3 簇数量k的选取

在k-means中最重要的参数毫无疑问就是k的选择了，但是因为是无监督学习，尤其是高维特征的时候，通常并不容易判断。一般来说，主要有下面三种方法来确定：

1. 如果有数据先验经验的话，则优先尝试经验值。例如，在手写数字识别中，有十个数字，那么在学习的时候应首先尝试k为10，在用户画像分类时，可以根据消费频率和消费金额分为四类等。
2. 如果对数据的分布没有先验认知，则可以通过7.1节提到的内部指标来选择，在选择的过程中，因为初始值的选择会对结果有影响，建议通过交叉验证的方式选择k值。
3. 可视化分析，可以通过降维方法，把特征降低到低维数据，可视化聚类结果，观察结果是否合理。

8. 实践

8.1 API

k-means API定义如下：

sklearn.cluster.KMeans(
n_clusters=8,   ##聚类簇数k
*, 
init='k-means++', ##初始质心选择方法，可选‘k-means++’, ‘random’或者自己指定初始质心
n_init=10,      ##用不同的初始化质心运行算法的次数。由于K-Means是结果受初始值影响的局部最优的迭代算法，因此需要多跑几次以选择一个较好的聚类效果，默认是10，一般不需要改。如果你的k值较大，则可以适当增大这个值。
max_iter=300,   ##最大迭代次数
tol=0.0001,     ##收敛容度，小于该值就认为收敛
precompute_distances='deprecated',  ##已废弃
verbose=0, 
random_state=None, 
copy_x=True, ##当我们precomputing distances时，将数据中心化会得到更准确的结果。如果把此参数值设为True，则原始数据不会被改变。如果是False，则会直接在原始数据上做修改并在函数返回值时将其还原。但是在计算过程中由于有对数据均值的加减运算，所以数据返回后可能会有细小差别。
n_jobs='deprecated', 
algorithm='auto'  ##可选“auto”, “full”, “elkan”。"full"就是我们传统的K-Means算法， “elkan”是我们原理篇讲的elkan K-Means算法。默认的"auto"则会根据数据值是否是稀疏的，来决定如何选择"full"和“elkan”。一般数据是稠密的，那么就是 “elkan”，否则就是"full"。一般默认即可
)

另外需要注意的是，k-means学习的时候是支持设置样本权重的：fit(X[, y, sample_weight])，例如设置为2，就相当于把该样本复制了一份副本。这里的 y 是无用参数，只是为了符合sklearn的API格式设置的。

MiniBatchKMeans API定义如下：

sklearn.cluster.MiniBatchKMeans(
n_clusters=8, *, 
init='k-means++', 
max_iter=100, 
batch_size=100,    ## Mini Batch KMeans算法的采样集的大小，默认是100.如果发现数据集的类别较多或者噪音点较多，需要增加这个值以达到较好的聚类效果。
verbose=0, 
compute_labels=True,   ## Mini Batch收敛之后计算标签和误差距离
random_state=None, 
tol=0.0, 
max_no_improvement=10, ##连续多少个Mini Batch没有改善聚类效果的话，就停止算法， 和reassignment_ratio， max_iter一样是为了控制算法运行时间的。默认是10.一般用默认值就足够了。
init_size=None,    ##用来做质心初始值候选的样本个数，默认是batch_size的3倍
n_init=3, 
reassignment_ratio=0.01  ##某个类别质心被重新赋值的最大次数比例，这个和max_iter一样是为了控制算法运行时间的。这个比例是占样本总数的比例，乘以样本总数就得到了每个类别质心可以重新赋值的次数。如果取值较高的话算法收敛时间可能会增加，尤其是那些暂时拥有样本数较少的质心，但值越高，效果会越好。默认是0.01。如果数据量不是超大的话，比如1w以下，建议使用默认值。如果数据量超过1w，类别又比较多，可能需要适当减少这个比例值。具体要根据训练集来决定。
)

8.2 应用实践

下面是一个通过k-means完成文本20个主题分类的案例，文本向量化通过TF-IDF和HashingVectorizer完成。

from sklearn.datasets import fetch_20newsgroups
from sklearn.decomposition import TruncatedSVD
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.feature_extraction.text import HashingVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import Normalizer
from sklearn import metrics
from sklearn.cluster import KMeans, MiniBatchKMeans

import logging
from optparse import OptionParser
import sys
from time import time
import numpy as np

op = OptionParser()
op.add_option("--lsa",
              dest="n_components", type="int",
              help="Preprocess documents with latent semantic analysis.")
op.add_option("--no-minibatch",
              action="store_false", dest="minibatch", default=True,
              help="Use ordinary k-means algorithm (in batch mode).")
op.add_option("--no-idf",
              action="store_false", dest="use_idf", default=True,
              help="Disable Inverse Document Frequency feature weighting.")
op.add_option("--use-hashing",
              action="store_true", default=False,
              help="Use a hashing feature vectorizer")
op.add_option("--n-features", type=int, default=10000,
              help="Maximum number of features (dimensions)"
                   " to extract from text.")
op.add_option("--verbose",
              action="store_true", dest="verbose", default=False,
              help="Print progress reports inside k-means algorithm.")

def is_interactive():
    return not hasattr(sys.modules['__main__'], '__file__')


# work-around for Jupyter notebook and IPython console
argv = [] if is_interactive() else sys.argv[1:]
(opts, args) = op.parse_args(argv)
if len(args) > 0:
    op.error("this script takes no arguments.")
    sys.exit(1)

categories = [
    'alt.atheism',
    'talk.religion.misc',
    'comp.graphics',
    'sci.space',
]

print("Loading 20 newsgroups dataset for categories:")
print(categories)

dataset = fetch_20newsgroups(subset='all', categories=categories,
                             shuffle=True, random_state=42)

print("%d documents" % len(dataset.data))
print("%d categories" % len(dataset.target_names))
print()

labels = dataset.target
true_k = np.unique(labels).shape[0]

print("Extracting features from the training dataset "
      "using a sparse vectorizer")

if opts.use_hashing:
    if opts.use_idf:
        # Perform an IDF normalization on the output of HashingVectorizer
        hasher = HashingVectorizer(n_features=opts.n_features,
                                   stop_words='english', alternate_sign=False,
                                   norm=None)
        vectorizer = make_pipeline(hasher, TfidfTransformer())
    else:
        vectorizer = HashingVectorizer(n_features=opts.n_features,
                                       stop_words='english',
                                       alternate_sign=False, norm='l2')
else:
    vectorizer = TfidfVectorizer(max_df=0.5, max_features=opts.n_features,
                                 min_df=2, stop_words='english',
                                 use_idf=opts.use_idf)
X = vectorizer.fit_transform(dataset.data)

print("done in %fs" % (time() - t0))
print("n_samples: %d, n_features: %d" % X.shape)

if opts.n_components:
    print("Performing dimensionality reduction using LSA")
    t0 = time()
    # Vectorizer results are normalized, which makes KMeans behave as
    # spherical k-means for better results. Since LSA/SVD results are
    # not normalized, we have to redo the normalization.
    svd = TruncatedSVD(opts.n_components)
    normalizer = Normalizer(copy=False)
    lsa = make_pipeline(svd, normalizer)

    X = lsa.fit_transform(X)

    print("done in %fs" % (time() - t0))

    explained_variance = svd.explained_variance_ratio_.sum()
    print("Explained variance of the SVD step: {}%".format(
        int(explained_variance * 100)))

    print()

if opts.minibatch:
    km = MiniBatchKMeans(n_clusters=true_k, init='k-means++', n_init=1,
                         init_size=1000, batch_size=1000, verbose=opts.verbose)
else:
    km = KMeans(n_clusters=true_k, init='k-means++', max_iter=100, n_init=1,
                verbose=opts.verbose)

print("Clustering sparse data with %s" % km)
t0 = time()
km.fit(X)
print("done in %0.3fs" % (time() - t0))
print()

print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels, km.labels_))
print("Completeness: %0.3f" % metrics.completeness_score(labels, km.labels_))
print("V-measure: %0.3f" % metrics.v_measure_score(labels, km.labels_))
print("Adjusted Rand-Index: %.3f"
      % metrics.adjusted_rand_score(labels, km.labels_))
print("Silhouette Coefficient: %0.3f"
      % metrics.silhouette_score(X, km.labels_, sample_size=1000))

if not opts.use_hashing:
    print("Top terms per cluster:")

    if opts.n_components:
        original_space_centroids = svd.inverse_transform(km.cluster_centers_)
        order_centroids = original_space_centroids.argsort()[:, ::-1]
    else:
        order_centroids = km.cluster_centers_.argsort()[:, ::-1]

    terms = vectorizer.get_feature_names()
    for i in range(true_k):
        print("Cluster %d:" % i, end='')
        for ind in order_centroids[i, :10]:
            print(' %s' % terms[ind], end='')
        print()

  在实际应用中，聚类算法并不局限于单独应用，可以和其他算法结合应用，例如聚类结果作为新的结果特征输入 LR 模型等，类似于 RF 中的特征嵌入。

参考文献

[1] https://www.cnblogs.com/pinard/p/6164214.html

[2] https://blog.csdn.net/sinat_26917383/article/details/51611519

[3] https://blog.csdn.net/sinat_26917383/article/details/70577710

[4] http://www.360doc.com/content/19/0525/15/99071_838117683.shtml

[5] https://zhuanlan.zhihu.com/p/34330242

[6] https://www.zhihu.com/question/19982667