数据结构之单链表(c语言附完整代码)
文章目录
- 定义
- 基本运算
- 完整代码
定义
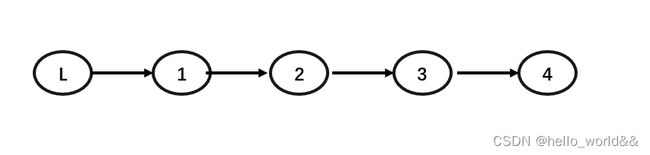
单链表是一种链式存取的数据结构,用一组地址任意的存储单元存放线性表中的数据元素。链表中的数据是以结点来表示的,每个结点的构成:元素(数据元素的映象) + 指针(指示后继元素存储位置),元素就是存储数据的存储单元,指针就是连接每个结点的地址数据。
示意图:
声明单链表
typedef struct LNode
{
ElemType data; //数据域
struct LNode *next; //指针域,指向后继结点
} LinkNode; //声明单链表结点类型
注意:本文章讨论的单链表是带头结点的单链表。
增加头结点的优点如下:
1.单链表中首结点的插入和删除操作与其他结点一致,无需进行特殊处理。
2.无论单链表是否为空都有一个头结点,因此统一了空表和非空表的处理过程。
基本运算
头插法建立单链表
void CreateListF(LinkNode *&L,ElemType a[],int n)
//头插法建立单链表
{
LinkNode *s;
L=(LinkNode *)malloc(sizeof(LinkNode)); //创建头结点
L->next=NULL;
for (int i=0;i<n;i++)
{
s=(LinkNode *)malloc(sizeof(LinkNode));//创建新结点s
s->data=a[i];
s->next=L->next; //将结点s插在原开始结点之前,头结点之后
L->next=s;
}
}
该运算依次从数组a中读取数据,生成一个新的结点,将该数据储放到新结点的数据域,然后将其插入到当前链表的表头(即头结点之后),直到所有的数据读完为止。
例如:数组 a={ 1,2,3,4 },使用头插法得到的链表顺序为 4,3,2,1。
插入操作如下:
s->next=L->next;
L->next=s;
首先修改s结点的后继指针next,使其指向头节点L的后继指针next所指结点,然后修改头结点的后继指针next,使其指向s结点。
本算法的时间复杂度为O(n)
尾插法建立单链表
void CreateListR(LinkNode *&L,ElemType a[],int n)
//尾插法建立单链表
{
LinkNode *s,*r;
L=(LinkNode *)malloc(sizeof(LinkNode)); //创建头结点
L->next=NULL;
r=L; //r始终指向终端结点,开始时指向头结点
for (int i=0;i<n;i++)
{
s=(LinkNode *)malloc(sizeof(LinkNode));//创建新结点s
s->data=a[i];
r->next=s; //将结点s插入结点r之后
r=s;
}
r->next=NULL; //终端结点next域置为NULL
}
该运算依次从数组a中读取数据,生成一个新的结点,将该数据储放到新结点的数据域,然后将其插入到当前链表的表尾,直到所有的数据读完为止。其过程是设置一个指针r,让它始终指向当前链表的尾结点,每次插入一个新结点后,让r指向这个新结点,所有元素插入完后,将r所指结点(尾结点)的next域设置为NULL。
例如:数组 a={ 1,2,3,4 },使用尾插法得到的链表顺序为 1,2,3,4。
插入操作如下:
r->next=s;
r=s;
首先修改r结点的后继指针next,使其指向s结点,最后让r指向s结点。
本算法的时间复杂度为O(n)
初始化单链表
void InitList(LinkNode *&L)
{
L=(LinkNode *)malloc(sizeof(LinkNode)); //创建头结点
L->next=NULL; //后续节点置空
}
该运算建立一个空的单链表,其过程是创建一个头结点,并将其next域置为NULL。
本算法的时间复杂度为O(1)
销毁单链表
void DestroyList(LinkNode *&L)
{
LinkNode *pre=L,*p=pre->next;
while (p!=NULL)
{ free(pre);
pre=p;
p=pre->next;
}
free(pre); //此时p为NULL,pre指向尾结点,释放它
}
该运算释放单链表L占用的内存空间,即逐一释放全部结点存储空间。设置p,pre两个指针指向两个相邻的结点,初始时pre指向头节点,p指向首结点(链表第一个元素),当p不为NULL执行循环:先释放pre,然后pre,p同步后移一个结点。循环结束时,pre指向尾结点,再将其释放。
本算法的时间复杂度为O(n)
判断单链表是否为空表
bool ListEmpty(LinkNode *L)
{
return(L->next==NULL);
}
该运算判断单链表是否为空表,当头结点的next域为NULL时,表示链表为空,返回1,否则返回0。
本算法的时间复杂度为O(1)
求单链表长度
int ListLength(LinkNode *L)
{
LinkNode *p=L;int i=0;
while (p->next!=NULL)
{ i++;
p=p->next;
}
return(i);
}
该运算返回链表L中数据元素的个数,设置指针p(初始指向头节点),i(初始值为0)用来记录链表中结点的个数,遍历链表,当p不为NULL时执行循环:i加1,p指向下一个结点。循环结束后返回i。
本算法的时间复杂度为O(n)
输出单链表
void DispList(LinkNode *L)
{
LinkNode *p=L->next;
while (p!=NULL)
{ printf("%d ",p->data);
p=p->next;
}
printf("\n");
}
该运算逐一输出各结点的data域值,设置指针p(初始指向首结点),p不为NULL执行循环:输出当前结点的数据域,p指向下一个结点。
本算法的时间复杂度为O(n)
求单链表中某个位置数据元素的值
bool GetElem(LinkNode *L,int i,ElemType &e)
{
int j=0;
LinkNode *p=L;
if (i<=0)
return false; //i错误返回假
while (j<i && p!=NULL)
{ j++;
p=p->next;
}
if (p==NULL) //不存在第i个数据结点
return false;
else //存在第i个数据结点
{ e=p->data;
return true;
}
}
该运算在单链表L中从开始找到第i个结点,如果存在第i个结点则将其data域值赋给e。设置指针p(初始指向头结点),j(初始值为0)用来记录遍历过的结点个数,当j
按元素的值查找
int LocateElem(LinkNode *L,ElemType e)
{
LinkNode *p=L->next;
int i=1;
while (p!=NULL && p->data!=e)
{ p=p->next;
i++;
}
if (p==NULL)
return(0);
else
return(i);
}
该运算在单链表中从头开始找到第一个data域值与e相等的结点,如果存在这样的结点,则返回逻辑序号,否则返回0。设置指针p(初始指向首结点),i(初始值为1),当p不为NULL且p结点的data域值不等于e时执行循环:p指向下一个结点,i加1。循环结束时有两种情况:如果p=NULL,表示不存在值为e的结点,返回0;否则表示存在值为e的结点,返回其逻辑序号i。
本算法的时间复杂度为O(n)
插入数据元素
bool ListInsert(LinkNode *&L,int i,ElemType e)
{
int j=0;
LinkNode *p=L,*s;
if (i<=0)
return false; //i错误返回假
while (j<i-1 && p!=NULL) //查找第i-1个结点p
{ j++;
p=p->next;
}
if (p==NULL) //未找到位序为i-1的结点
return false;
else //找到位序为i-1的结点*p
{ s=(LinkNode *)malloc(sizeof(LinkNode));//创建新结点*s
s->data=e;
s->next=p->next; //将s结点插入到结点p之后
p->next=s;
return true;
}
}
该运算在单链表第i个结点前插入值为e的结点。
实现过程是先在单链表L中找到第i-1个结点,用p指向它。如果存在这样的结点,将值为e的结点(指针s所指结点)插入到p结点的后面。设置指针p(初始指向头结点),i(初始值为0),当j
s->next=p->next;
p->next=s;
此处插入操作与头插法建立单链表的插入操作相同(头插法建立单链表时的插入操作相当于把s结点插入到头结点L之后),此处是把s结点插入到p结点之后。
本算法的时间复杂度为O(n)
动画演示:
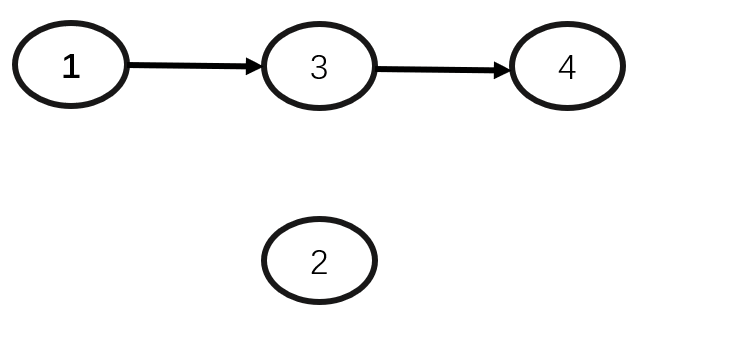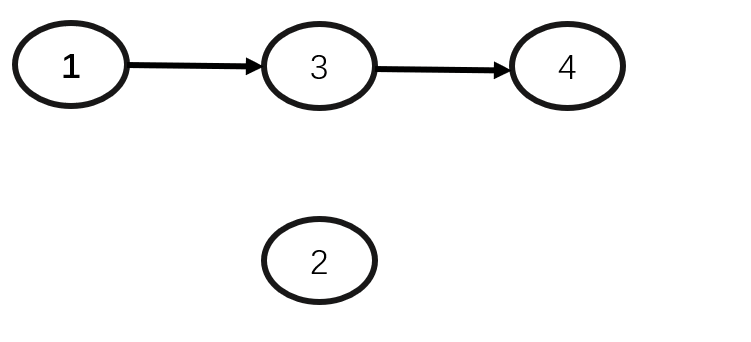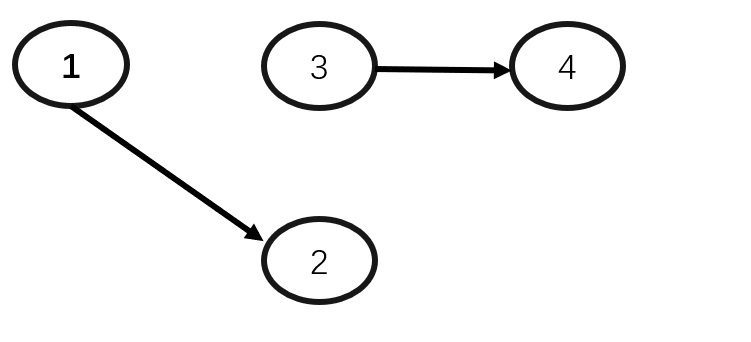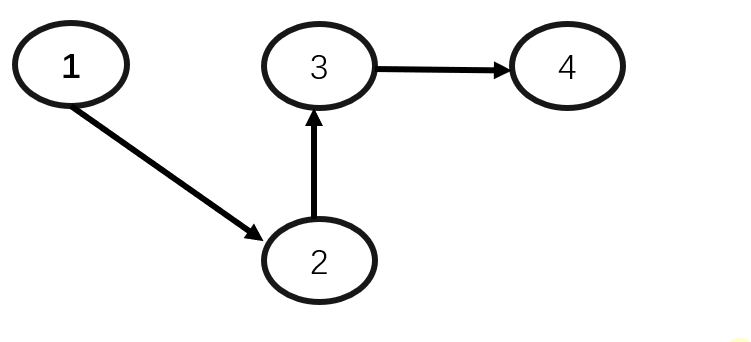
删除数据元素
bool ListDelete(LinkNode *&L,int i,ElemType &e)
{
int j=0;
LinkNode *p=L,*q;
if (i<=0)
return false; //i错误返回假
while (j<i-1 && p!=NULL) //查找第i-1个结点
{ j++;
p=p->next;
}
if (p==NULL) //未找到位序为i-1的结点
return false;
else //找到位序为i-1的结点p
{ q=p->next; //q指向要删除的结点
if (q==NULL)
return false; //若不存在第i个结点,返回false
e=q->data;
p->next=q->next; //从单链表中删除q结点
free(q); //释放q结点
return true;
}
}
该运算删除单链表L中第i个结点,并将其data域值赋给e。实现过程是先在单链表中找到第i-1个结点,用p指向它。如果存在这样的结点,且存在后继结点(q所指结点),则删除q所指结点。设置指针p(初始指向头结点),j(初始值为0),当j
p->next=q->next; //从单链表中删除q结点
直接修改p结点的后继指针next,使其指向q结点的后继指针next所指的结点。
本算法的时间复杂度为O(n)
动画演示:
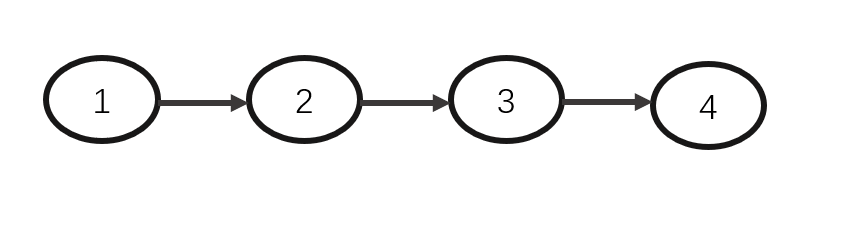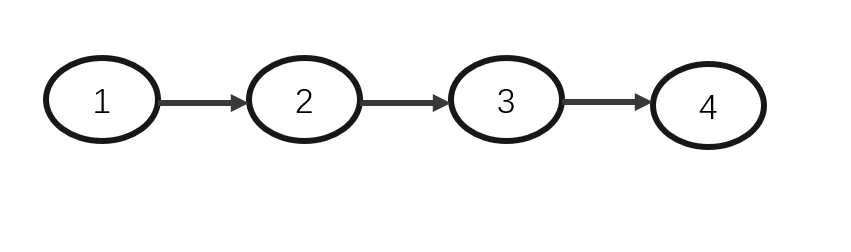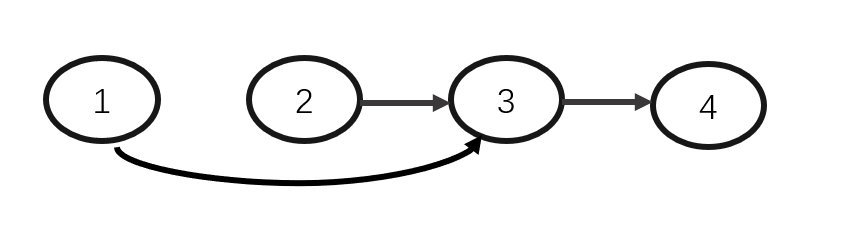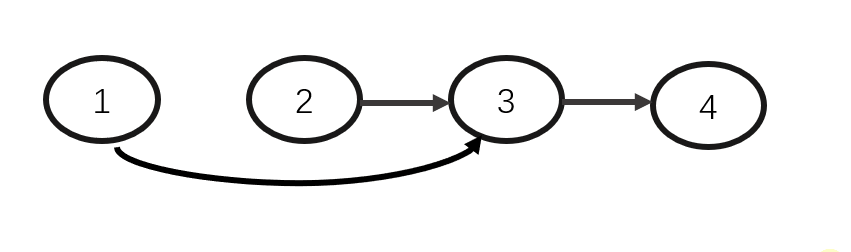
完整代码
#include 参考资料:
李春葆《数据结构教程》(第五版)
维基百科