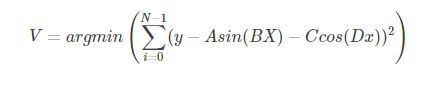g2o非线性优化
基于g2o的最小二乘方法。
g2o,即General Graph Optimization,他是一个基于图理论的优化库。图优化理论介绍,可以参考半闲居士的博客
有这么一个问题,给你一组二维数据,拟合其直线方程。
譬如下面的方程:
拟合y=Asin(Bx)+Ccos(Dx)y=Asin(Bx)+Ccos(Dx),已知N组数据(xi,yi),i=0,1,⋯N−1(xi,yi),i=0,1,⋯N−1,待优化变量V=[A,B,C,D]V=[A,B,C,D]
整个图中,只有一个顶点,其待优化变量V(即参数A,B,C,D),连接只有一个顶点的边即一元边(Unary Edge),使用g2o优化步骤如下:
- 定义顶点和边的类型(继承自g2o)
- 选择优化算法
- 构建图(添加顶点和边)
- 优化,调用g2o优化,返回结果
顶点的定义:
继承BaseVertex<定点byte数,顶点结构体>类
实现setToRiginImpl()函数,里面给_estimate成员函数赋初值
_estimate的类型就是模板里指定的顶点结构体
实现:oplusImpl(const double * update_)。update_是指向跟新值得指针,使用前需要转换成真实的结 构类型。不一定是顶点类型。比如update_可以是李代数,但顶点类型是李群。
可以使用esitimate()函数得到顶点的值,类型同上面的顶点结构体。
边的定义:
继承BaseBinaryEdge<观察值byte数,观察值结构体,第一个顶点的类型,第二个顶点的类型>(两个顶点的边)
或继承BaseUnaryEdge<观察值byte数,观察值结构体,顶点的类型>(一个顶点的边)
实现函数computeError(),函数里面需要计算_error的值,其他顶点和测量值的成员变量参考其他例子。
实现linearizeOplus(),单顶点的计算_jacobianOplusXi矩阵,双顶点的还要计算_jacobianOplusXj矩阵
SE3Quat
使用map函数来变换一个3d点
SparseOptimizer
这个应该是总的流程和数据管理器
setAlgorithm设置具体计算更新值得算法
addVertex加入顶点
addEdge()
addParameter()可以传入一些超参
initializeOptimization()给顶点填入初始值
optimize()启动优化流程
调用所有边的linearizeOplus()函数,得到每个边的雅克比矩阵,然后把矩阵连接成一个大矩阵
调用所有边的computeError(),得到误差矩阵
基于雅克比和误差,使用优化器计算更新值deltaX(矩阵求逆,主要时间花费在这里)
把deltaX拆分成各个顶点的值
调用顶点的oplusImpl函数,更新顶点的_estimate变量
回到第一步
1)定义顶点和边的类型
由于g2o没有本例中的顶点和边,故需要自己定义顶点和边的类型,其继承自BaseVertex和BaseEdge,可以参考相机位姿和3D点坐标常用的几种类型VertexSE3Expmap、VertexSBAPointXYZ、EdgeSE3ProjectXYZ、EdgeSE3ProjectXYZOnlyPose
定义方式1
class CurveFittingVertex :public g2o::BaseVertex<4, Vector4d>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingVertex();
virtual void setToOriginImpl()
{
_estimate << 0, 0, 0, 0;
}
virtual void oplusImpl(const double* update_);
bool read(std::istream& is) { return 0; }
bool write(std::ostream& os)const { return 0; }
};
CurveFittingVertex::CurveFittingVertex():BaseVertex<4,Eigen::Vector4d>()
{}
void CurveFittingVertex::oplusImpl(const double* update_)
{
Eigen::Map up(update_);
_estimate += up;
}
class CurveFittingEdge :public g2o::BaseUnaryEdge<1, double, CurveFittingVertex>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingEdge();
void computeError();
virtual void linearizeOplus();
bool read(std::istream& is) { return 0; }
bool write(std::ostream& os)const { return 0; }
public:
double _x;
};
CurveFittingEdge::CurveFittingEdge():g2o::BaseUnaryEdge<1,double,CurveFittingVertex>()
{}
void CurveFittingEdge::computeError()
{
const CurveFittingVertex* v = static_cast(_vertices[0]);
const Vector4d abcd = v->estimate();
_error(0, 0) = _measurement - (abcd[0] * sin(abcd[1] * _x) + abcd[2] * cos(abcd[3] * _x));
}
void CurveFittingEdge::linearizeOplus()
{
CurveFittingVertex *vi = static_cast(_vertices[0]);
Vector4d abcd = vi->estimate();
_jacobianOplusXi(0, 0) = -sin(abcd[1] * _x);
_jacobianOplusXi(0, 1) = -abcd[0] * _x*cos(abcd[1] * _x);
_jacobianOplusXi(0, 2) = -cos(abcd[3] * _x);
_jacobianOplusXi(0, 3) = abcd[2] * _x*sin(abcd[3] * _x);
} 定义方式2
class CurveFittingVertex :public g2o::BaseVertex<4, Vector4d>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingVertex() {}
virtual void setToOriginImpl() {}
virtual bool read(std::istream& is) { return 0; }
virtual bool write(std::ostream& os)const { return 0; }
virtual void oplusImpl(const double* update)
{
_estimate += Eigen::Vector4d::ConstMapType(update);
}
};
class CurveFittingEdge :public g2o::BaseUnaryEdge<2, Eigen::Vector2d, CurveFittingVertex>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingEdge(){}
bool read(std::istream& is) { return 0; }
bool write(std::ostream& os)const { return 0; }
void computeError()
{
const CurveFittingVertex* v = static_cast(_vertices[0]);
const Vector4d abcd = v->estimate();
_error(0) = measurement()(1)- (abcd[0] * sin(abcd[1] * measurement()(0)) + abcd[2] * cos(abcd[3] * measurement()(0)));
}
//virtual void linearizeOplus();
}; 注意两种方式的区别,其中第二种方式中,我们没有定义计算雅克比的方法,这里会默认使用数值求导方法。如果我们能够推导出雅可比矩阵的解析形式并告诉优化库,就可以避免数值求导中的诸多问题
2)选择优化算法
// 构建图优化,先设定g2o
// 矩阵块:每个误差项优化变量维度为4 ,误差值维度为1
typedef g2o::BlockSolver< g2o::BlockSolverTraits<4, 1> > Block;
// 线性方程求解器:稠密的增量方程
Block::LinearSolverType* linearSolver = new LinearSolverDense();
Block* solver_ptr = new Block(std::unique_ptr(linearSolver)); // 矩阵块求解器
// 梯度下降方法,从GN, LM, DogLeg 中选
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(std::unique_ptr(solver_ptr));
// g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
// g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出 3)构建图
// 往图中增加顶点
CurveFittingVertex *v = new CurveFittingVertex();
// 设置优化初始估计值
v->setEstimate(Eigen::Vector4d(1.6, 1.4, 6.2, 1.7));
v->setId(0);
v->setFixed(false);
optimizer.addVertex(v);
// 往图中增加边
for (int i = 0; i < N; i++)
{
CurveFittingEdge* edge = new CurveFittingEdge();
edge->setId(i + 1);
edge->setVertex(0, v); // 设置连接的顶点
#ifdef TEST!
edge->setMeasurement(y_data[i]); // 观测数值
edge->_x = x_data[i];
#else
edge->setMeasurement(Eigen::Vector2d(x_data[i], y_data[i]));
#endif
// 信息矩阵:协方差矩阵之逆
edge->setInformation(Eigen::Matrix::Identity() * 1 / (w_sigma* w_sigma));
optimizer.addEdge(edge);
} 4)优化
optimizer.initializeOptimization();
optimizer.optimize(100);完整代码如下:
#include
#include // 顶点类型
#include //一元边类型
#include //求解器的实现。主要来自choldmod, csparse。在使用g2o时要先选择其中一种。
#include //莱文贝格-马夸特方法(Levenberg–Marquardt algorithm)能提供数非线性最小化(局部最小)的数值解。
#include //高斯牛顿法
#include //Dogleg(狗腿方法)
#include
#include //矩阵库
#include //opencv2
#include //数学库
#include
#include
#include //时间库
using namespace std;
using namespace g2o;
using namespace Eigen;
#ifdef TEST!
class CurveFittingVertex :public g2o::BaseVertex<4, Vector4d>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingVertex();
virtual void setToOriginImpl()
{
_estimate << 0, 0, 0, 0;
}
virtual void oplusImpl(const double* update_);
bool read(std::istream& is) { return 0; }
bool write(std::ostream& os)const { return 0; }
};
CurveFittingVertex::CurveFittingVertex():BaseVertex<4,Eigen::Vector4d>()
{}
void CurveFittingVertex::oplusImpl(const double* update_)
{
Eigen::Map up(update_);
_estimate += up;
}
class CurveFittingEdge :public g2o::BaseUnaryEdge<1, double, CurveFittingVertex>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingEdge();
void computeError();
virtual void linearizeOplus();
bool read(std::istream& is) { return 0; }
bool write(std::ostream& os)const { return 0; }
public:
double _x;
};
CurveFittingEdge::CurveFittingEdge():g2o::BaseUnaryEdge<1,double,CurveFittingVertex>()
{}
void CurveFittingEdge::computeError()
{
const CurveFittingVertex* v = static_cast(_vertices[0]);
const Vector4d abcd = v->estimate();
_error(0, 0) = _measurement - (abcd[0] * sin(abcd[1] * _x) + abcd[2] * cos(abcd[3] * _x));
}
void CurveFittingEdge::linearizeOplus()
{
CurveFittingVertex *vi = static_cast(_vertices[0]);
Vector4d abcd = vi->estimate();
_jacobianOplusXi(0, 0) = -sin(abcd[1] * _x);
_jacobianOplusXi(0, 1) = -abcd[0] * _x*cos(abcd[1] * _x);
_jacobianOplusXi(0, 2) = -cos(abcd[3] * _x);
_jacobianOplusXi(0, 3) = abcd[2] * _x*sin(abcd[3] * _x);
}
#else
class CurveFittingVertex :public g2o::BaseVertex<4, Vector4d>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingVertex() {}
virtual void setToOriginImpl() {}
virtual bool read(std::istream& is) { return 0; }
virtual bool write(std::ostream& os)const { return 0; }
virtual void oplusImpl(const double* update)
{
_estimate += Eigen::Vector4d::ConstMapType(update);
}
};
class CurveFittingEdge :public g2o::BaseUnaryEdge<2, Eigen::Vector2d, CurveFittingVertex>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingEdge(){}
bool read(std::istream& is) { return 0; }
bool write(std::ostream& os)const { return 0; }
void computeError()
{
const CurveFittingVertex* v = static_cast(_vertices[0]);
const Vector4d abcd = v->estimate();
_error(0) = measurement()(1)- (abcd[0] * sin(abcd[1] * measurement()(0)) + abcd[2] * cos(abcd[3] * measurement()(0)));
}
//virtual void linearizeOplus();
};
#endif // TEST!
int main()
{
double a = 5.0, b = 1.0, c = 10.0, d = 2.0; // 真实参数值
int N = 100;
double w_sigma = 2.0; // 噪声值Sigma
cv::RNG rng; // 随机数产生器OpenCV
double abcd[4] = { 0, 0, 0, 0 }; // 参数的估计值abc
vector x_data, y_data;
cout << "generate random data" << endl;
for (int i = 0; i < N; i++)
{
//generate a random variable [-10 10]
double x = rng.uniform(-10., 10.);
double y = a * sin(b*x) + c * cos(d *x) + rng.gaussian(w_sigma);
x_data.push_back(x);
y_data.push_back(y);
cout << x_data[i] << " , " << y_data[i] << endl;
}
// 构建图优化,先设定g2o
// 矩阵块:每个误差项优化变量维度为4 ,误差值维度为1
typedef g2o::BlockSolver< g2o::BlockSolverTraits<4, 1> > Block;
// 线性方程求解器:稠密的增量方程
Block::LinearSolverType* linearSolver = new LinearSolverDense();
Block* solver_ptr = new Block(std::unique_ptr(linearSolver)); // 矩阵块求解器
// 梯度下降方法,从GN, LM, DogLeg 中选
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(std::unique_ptr(solver_ptr));
// g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
// g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出
// 往图中增加顶点
CurveFittingVertex *v = new CurveFittingVertex();
// 设置优化初始估计值
v->setEstimate(Eigen::Vector4d(1.6, 1.4, 6.2, 1.7));
v->setId(0);
v->setFixed(false);
optimizer.addVertex(v);
// 往图中增加边
for (int i = 0; i < N; i++)
{
CurveFittingEdge* edge = new CurveFittingEdge();
edge->setId(i + 1);
edge->setVertex(0, v); // 设置连接的顶点
#ifdef TEST!
edge->setMeasurement(y_data[i]); // 观测数值
edge->_x = x_data[i];
#else
edge->setMeasurement(Eigen::Vector2d(x_data[i], y_data[i]));
#endif
// 信息矩阵:协方差矩阵之逆
edge->setInformation(Eigen::Matrix::Identity() * 1 / (w_sigma* w_sigma));
optimizer.addEdge(edge);
}
// 执行优化
cout << "strat optimization" << endl;
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
optimizer.initializeOptimization();
optimizer.optimize(100);
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration time_used = chrono::duration_cast> (t2 - t1);
cout << "solve time cost = " << time_used.count() << " seconds." << endl;
// 输出优化值
Eigen::Vector4d abcd_estimate = v->estimate();
cout << "estimated module: " << endl << abcd_estimate << endl;
system("pause");
return 0;
}
参考:
https://blog.csdn.net/stihy/article/details/55254756
https://github.com/tiger20/g2o_surface_fit
https://blog.csdn.net/ziliwangmoe/article/details/81460392