机器学习：Logistic回归处理用气象数据预测森林火灾的数据挖掘方法

---

线性模型与回归

目的： 学习一个线性模型以尽可能准确地预测实值输出标记。

其中，yi为实际观察值，f（xi）是回归值。
一般形式：

其中x=(x1, x2, …, xd)是由d维属性描述的样本，其中 xi是 x 在 第 i 个属性上的取值。
向量形式：

其中w=(w1, w2, …, wd)为待求解系数。

举个简单的例子来说明，之前写过的博客有写过歌坛常青树的判定因素，x1，x2，x3…就可以分别用来指代，歌手的年龄、唱功音区（高，中，低）、性别（男，女），而w1、w2、w3…分别为
其所对应的系数，系数越大说明该属性越重要。

最小二乘与参数求解

1.一维数据：

考虑xi是一维数据，设其回归值f(xi)与实际观察yi之间存在的 误差 ei，则学习的目标为：

误差 ei=| f(xi)-yi |，代入数据可得

最小化均方误差：

分别对w和b求导，可得：

得到解析/闭合（closed-form）解：

2.多维数据

多元线性回归目标：

给定数据集：

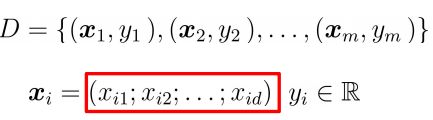
把 w 和 b 整合成向量形式 （w；b）数据集可表示为:


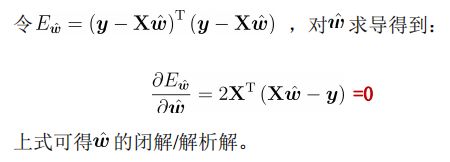
得到解析解如下：

则线性回归模型：

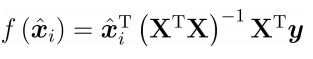
最大似然估计

最大似然估计：
找到 β0，β1 值让似然概率最大化

目标函数 损失函数（代价函数 cost functon）：
参数估计优化的目标->损失最小化
对数似然损失函数 (log-likehood loss function)

对β 优化求解的算法：梯度下降
寻找让损失函数 J(β)J(β) 取得最小值时的 β

正则化：
损失函数中增加惩罚项：参数值越大惩罚越大–>让算法去尽量减少参数值
损失函数 J(β)：

● 当模型参数 β 过多时，损失函数会很大，算法要努力减少 β 参数值来让损失函数最小。
● λ 正则项重要参数，λ 越大惩罚越厉害，模型越欠拟合，反之则倾向过拟合。

Logistic回归

基本介绍

1、回归：用一条直线（该线称之为最佳拟合直线）对存在的一些数据点进行拟合，这个拟合过程就叫回归。回归就是要找到最佳拟合参数集。回归就是预测一系列连续的值，分类就是预测一系列离散的值
线性“回归”，模型的目的是预测，方式是“回归”，有“倒推”之意在里面。（倒推就是先建立线性模型（包含系数）然后用训练数据来倒推出误差最小的参数。
2、主要思想：根据现有数据对分类边界线建立回归公式，以此来分类。
3、训练分类器：找到最佳拟合参数集，使用最优化算法。
接下来，介绍二值型输出分类器的相关原理。

基于Logistic回归和Sigmoid函数的分类

我们要做的是二值型输出分类器，即有0和1。将因变量可能属于的两个类分别称为负向类和正向类，其中 0 表示负向类，1 表示正向类。

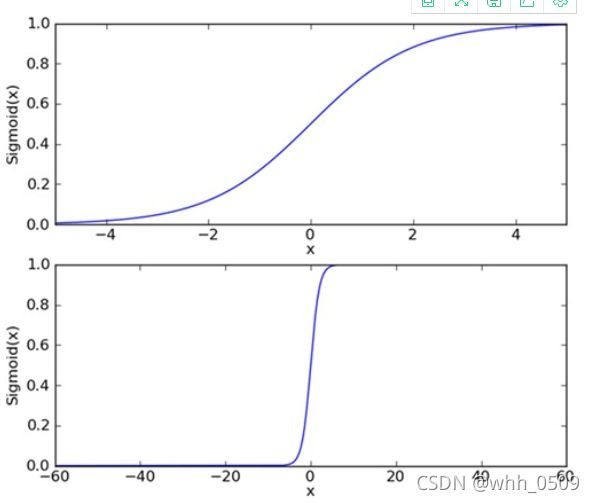
Sigmoid函数公式：

为了实现Logistic回归分类器，我们可以将每个属性乘上一个回归系数，再把所有结果之相加，将这个综合代入Sigmoid函数中，得到值域为[0,1]。

基于最优化方法的最佳回归系数确定

Sigmoid函数输入记为z：

写成向量形式：

其中，向量w是我们要找的最佳参数，向量x是分类器的输入数据。

最优化算法之梯度上升法

基本思想：沿着某函数的梯度方向探寻找到该函数的最大值。

梯度意味着要沿x的方向移动∂ f ( x , y ) ∂ x /∂x，沿y的方向移动∂ f ( x , y ) /∂ y，其中，函数f ( x , y ) f(x,y)f(x,y)必须要在待计算的点上有定义并且可微。如下图：

上图展示的，梯度上升算法到达每个点后都会重新估计移动的方向。从 P0 开始，计算完该点的梯度，函数就根据梯度移动到下一点 P1。在 P1 点，梯度再次被重新计算，并沿着新的梯度方向移动到 P2 。如此循环迭代，直到满足停止条件。迭代过程中，梯度算子总是保证我们能选取到最佳的移动方向。

上图中的梯度上升算法沿梯度方向移动了一步。可以看到，梯度算子总是指向函数值增长最快的方向。这里所说的是移动方向，而未提到移动量的大小。该量值称为步长，记作 α 。用向量来表示的话，梯度上升算法的迭代公式如下:

该公式将一直被迭代执行，直至达到某个停止条件为止，比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围。
所以，接下来我们要做的就是对l(β)求偏导：

则最终迭代公式写成：

训练算法：使用梯度上升找到最佳参数

如下图所示：图中有100个样本点，每个点有两个属性即X1和X2。我们将通过梯度上升法找到最佳回归系数，也就是拟合出Logistic回归模型的最佳参数。

将数据存在testSet.txt记事本中，如下图所示：
我们可以将这些数据当做训练模型参数的训练样本。见到训练样本就可以比较直观的理解算法的输入，以及我们如何利用这些数据来训练逻辑回归分类器，进而用训练好的模型来预测新的样本（检测样本）。

可以看出数据具有二维特征，因此可以将数据在一个二维平面上展示出来。我们可以将第一列数据为X1轴上的值，第二列数据为X2轴上的值。而最后一列数据即为分类标签。根据标签的不同，对这些点进行分类。
相关代码：

#打开文本读取每行的数据X1和X2
def loadDataSet():
    dataMat = []      #创建数据列表
    labelMat = []      #创建标签列表
    fr = open('testSet.txt')    #打开文件
    for line in fr.readlines():         #逐行读取
        lineArr = line.strip().split()       #去回车，放入列表
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])    #添加数据
        labelMat.append(int(lineArr[2]))      #添加标签
    fr.close()    #关闭文件
    return dataMat, labelMat    
    
#sigmoid函数
def sigmoid(inX):
    return 1.0/(1+exp(-inX))
    
#梯度上升算法
dataMatrix = np.mat(dataMatIn)  # 转换成numpy的mat
    labelMat = np.mat(classLabels).transpose()  # 转换成numpy的mat,并进行转置
    m, n = np.shape(dataMatrix)  # 返回dataMatrix的大小。m为行数,n为列数。
    alpha = 0.001  # 移动步长,也就是学习速率,控制更新的幅度。
    maxCycles = 500  # 最大迭代次数
    weights = np.ones((n, 1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * weights)  # 梯度上升矢量化公式
        error = labelMat - h
        weights = weights + alpha * dataMatrix.transpose() * error
    return weights.getA()  # 将矩阵转换为数组，返回权重数组

测试：

import logRegres
dataArr,labelMat=logRegres.loadDataSet()
print(logRegres.gradAscent(dataArr,labelMat))

结果：

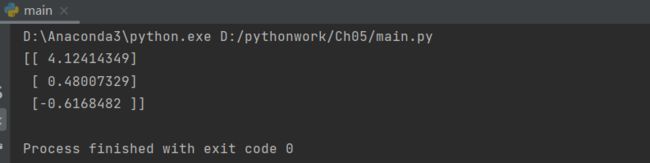
得到三个属性的回归系数，分别是4.12414349、 0.48007329、-0.6168482

分析数据：画出决策边界

通过上述实验，得到了数据的一组回归系数，简单说，就是确定了不同类别数据之间的分隔线。下面将介绍如何画出分隔线。
画出数据集和Logistic回归最佳拟合直线的函数：

def plotBestFit(wei):
    import matplotlib.pyplot as plt
    weights = wei.getA()
    dataMat,labelMat=loadDataSet()
    dataArr = array(dataMat)
    n = shape(dataArr)[0] 
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i])== 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = arange(-3.0, 3.0, 0.1)
    y = (-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x, y)
    plt.xlabel('X1'); plt.ylabel('X2');
    plt.show()

测试：

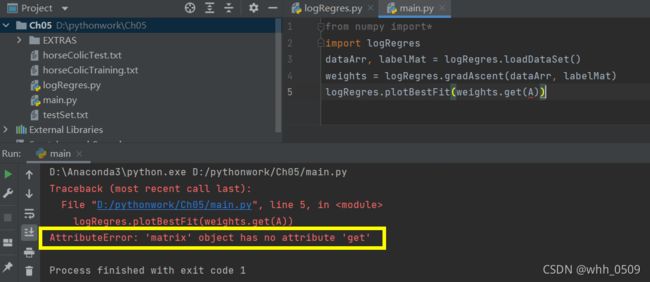
如果按上图测试，会出现报错，原因是版本问题，解决方法：删掉getA（）即可。

from numpy import*
import logRegres
dataArr, labelMat = logRegres.loadDataSet()
weights = logRegres.gradAscent(dataArr, labelMat)
logRegres.plotBestFit(weights)

输出的结果如图：

由图可得，只分错了两个到四个点。但是梯度上升算法在每次更新回归系数时都要遍历整个数据集，当样本有成千上万是，方法的计算复杂度就太高了。

训练算法：随机梯度上升

方法：一次仅用一个样本点来更新回归系数，代码如下：

def stocGradAscent0(dataMatrix, classLabels):
    m,n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)   #initialize to all ones
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights

随机梯度上升算法和梯度上升算法在代码上很相似，但有区别：
1、变量h和误差error都是向量，前者是数值
2、前者没有矩阵的转换过程，所有变量的数据类型都是Numpy数组
测试：

from numpy import*
import logRegres
dataArr, labelMat = logRegres.loadDataSet()
weights = logRegres.stocGradAscent0(array(dataArr), labelMat)
logRegres.plotBestFit(weights)

结果如图：

可以看出，效果不像，并不像上一个回归梯度上升算法那样完美，错分了将近三分之一的样本。

下图是运行随机梯度上升算法，在数据集的一次遍历中回归系数与迭代次数的关系图，回归系数经过大量迭代才能达到稳定值，并且仍然有局部的波动现象。

改进的随机梯度上升算法

相比于随机梯度上升算法，增加了两处代码来进行改进。代码如下：

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m,n = np.shape(dataMatrix)                                                #返回dataMatrix的大小。m为行数,n为列数。
    weights = np.ones(n)                                                       #参数初始化
    for j in range(numIter):                                           
        dataIndex = list(range(m))
        for i in range(m):           
            alpha = 4/(1.0+j+i)+0.01                                            #降低alpha的大小，每次减小1/(j+i)。
            randIndex = int(random.uniform(0,len(dataIndex)))                #随机选取样本
            h = sigmoid(sum(dataMatrix[randIndex]*weights))                    #选择随机选取的一个样本，计算h
            error = classLabels[randIndex] - h                                 #计算误差
            weights = weights + alpha * error * dataMatrix[randIndex]       #更新回归系数
            del(dataIndex[randIndex])                                         #删除已经使用的样本
    return weights                           

该算法第一个改进之处在于，alpha在每次迭代的时候都会调整，并且，虽然alpha会随着迭代次数不断减小，但永远不会减小到0，因为这里还存在一个常数项。必须这样做的原因是为了保证在多次迭代之后新数据仍然具有一定的影响。如果需要处理的问题是动态变化的，那么可以适当加大上述常数项，来确保新的值获得更大的回归系数。另一点值得注意的是，在降低alpha的函数中，alpha每次减少1/(j+i)，其中j是迭代次数，i是样本点的下标。第二个改进的地方在于跟新回归系数(最优参数)时，只使用一个样本点，并且选择的样本点是随机的，每次迭代不使用已经用过的样本点。这样的方法，就有效地减少了计算量，并保证了回归效果。

测试结果，如下图：

这次仅对数据做了150次的遍历，而之前的方法是做了500次的遍历。该分割线和gradAscent()差不多的效果，但是作用计算量更少。

改进后的随机梯度上升算法没有出现周期性波动，收敛得更快。可从下面的回归系数和迭代次数的关系图看出：

利用Logistic回归利用气象数据预测森林火灾的数据挖掘方法

数据准备

1、数据来源：
http://archive.ics.uci.edu/ml/datasets.php?format=&task=reg&att=&area=&numAtt=&numIns=100to1000&type=&sort=nameUp&view=table

选择森林火灾，共517条样本量，数据维度为13，符合实验要求。
利用python打乱517条样本，抽取其中的150条作为测试集，剩下即为训练集。

2、数据属性
将数据下载保存在firetraining.txt文件中：

从第1个到第13个属性分别表示：
1.蒙特西尼奥公园地图中的 X - x 轴空间坐标： 1到 9
2.蒙特西尼奥公园地图中的 Y - y 轴空间坐标： 2到 9
3.一年中的月 ： 1 到 12
4.一周中的一天：1到7
5.FFMC - FWI 系统的 FFMC 指数： 18.7 至 96.20
6.DMC - FWI 系统的 DMC 指数：1.1 到 291.3
7.FWI 系统的直流 - 直流指数： 7.9 到 860.6
8.ISI - FWI 系统的 ISI 指数：0.0 至 56.10
9.温度 - 温度在摄氏度： 2.2 至 33.30
10.RH - 相对湿度在 %： 15.0至 100
11.风速 - 风速公里/小时： 0.40 至 9.40
12.雨 - 外面雨毫米/m2 ： 0.0 至6.4
13.面积 - 森林的燃烧面积（在公顷）：0.00至1090.84（此输出变量非常偏向0.0，因此用对数转换建模可能有意义）。

其中第13项面积-森林的燃烧面积，当为0.00时即表示没有发生火灾，当为燃烧面积>0时，我们默认为发生火灾，即读取了每行的最后一个属性，判断是否发生火灾，如下述代码所示：

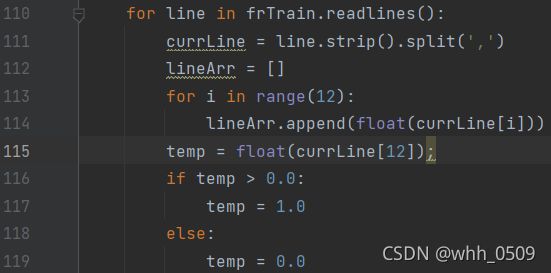
回归分类函数

1、计算Sigmoid值

以回归系数和特征向量作为输入来计算对应的Sigmoid值，如果Sigmoid值大于0.5函数返回1，否则返回0。

def classifyVector(inX, weights):
    prob = sigmoid(sum(inX * weights))
    if prob == 0.5:
        return 1.0
    else:
        return 0.0

2、从文本文件读取数据

从“firetraining.txt”中读取数据，放在数据集中，额外处理每行数据的最后一个属性（森林燃烧面积有0.00至1090.84，将大于0的通通化为1，这样即符合二值型输出分类器），测试的trainingSet数据集即读取了所有数据。

frTrain = open('firetraining.txt');
    trainingSet = [];
    trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split(',')
        lineArr = []
        for i in range(12):
            lineArr.append(float(currLine[i]))
        temp = float(currLine[12]);
        if temp > 0.0:
            temp = 1.0
        else:
            temp = 0.0
        lineArr.append(temp)
        trainingSet.append(lineArr)

3、打乱数据

为何要打乱？因为最初的数据集的数据位于前面的最后一列基本为0（燃烧面积为0，即没着火），直到最后才呈现出杂乱的感觉，为了减少偶然误差，于是打乱数据：

random.shuffle(trainingSet)

4.生成测试集和训练集

    trainingSet = array(trainingSet)
    trainingLabels = trainingSet[:, -1] #取每条样本最后一个属性
    trainingSet = trainingSet[:,:-1] #取每条样本除了最后一个属性之外的所有属性
    testSet = trainingSet[:150] #取前150条作为测试集，生成测试集
    testLabel = trainingLabels[:150] #取前150条作为测试集标签
    trainingSet = trainingSet[150:] #生成训练集
    trainingLabels= trainingLabels[150:]
    print(trainingLabels.shape, trainingSet.shape)
    print(testLabel.shape, testSet.shape)

输出结果：

5.计算回归系数向量

这里迭代的次数可以自由设定：

 trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 500)
    errorCount = 0;
    for i in range(len(testSet)):
        if int(classifyVector(testSet[i], trainWeights)) != testLabel[i]:
                errorCount += 1
    errorRate = (float(errorCount) / 150)
    print("the error rate of this test is: %f" % errorRate)
    return errorRate

6.测试

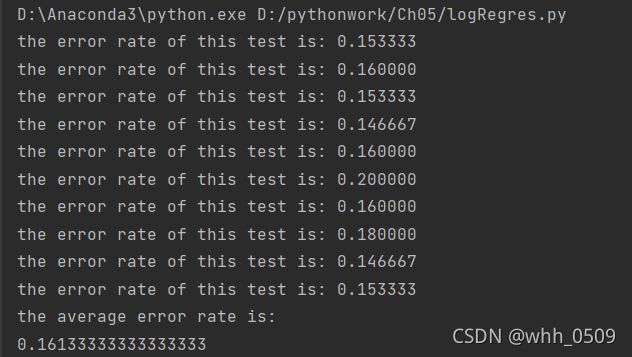
1.当在训练集上使用原始版随机梯度算法：

2.当在训练集上使用改进后的随机梯度算法：

2.1当在训练集上使用100次迭代时：

2.2当在训练集上使用500次迭代时：

小结

1、对比2.1和2.2：训练集使用500次迭代，实验结果是2.2的错误率明显降低了，表明迭代次数500次比迭代100次的效果更好，迭代次数不能少。
2、对比1和2，改进后的随机梯度算法虽然是错误率更低了，但是运行时间比较长，运行速度比较慢，而原始版随机梯度算法错误率比改进后的高，但是运行时间短。所以当数据集中数据较少的情况下，完全可以使用原始版的随机梯度算法。当数据较多时，使用改进后的随机梯度算法加以解决。

---

实验总结

本次实验，我借助了课程ppt和机器学习教材以及在csdn上阅读了大量博客，学习了逻辑回归，掌握线性回归、，解析数据使得数据符合决策树算法输入。但是在编写数据的时候，利用UCI机器学习数据库，导致实验结果理想，比上次决策树自己编的数据效果好多了。